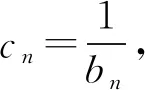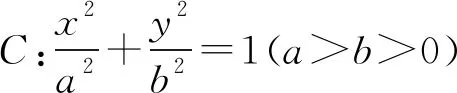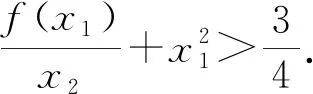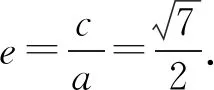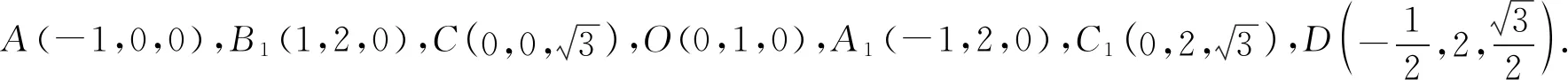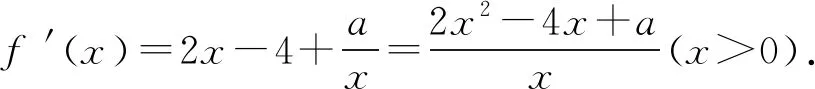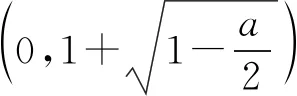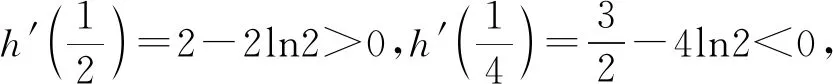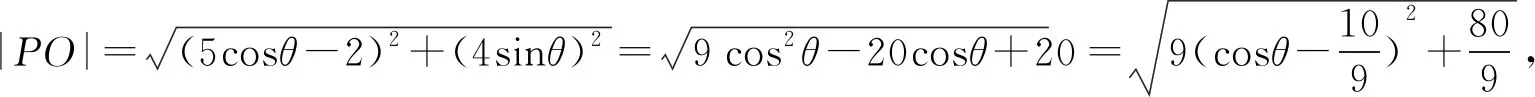2022年高考模拟试题(三)
2022-04-26张刚
张 刚
(安徽省宿州应用技术学校 234000)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若集合A={x∈Z|x2+2x≤0},则集合A的子集个数为( ).
A.3 B.6 C.8 D.9

A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.如图1,战国商鞅铜方升是公元前344年商鞅督造的标准量器.秦始皇统一中国后,仍以商鞅所规定的制度和标准统一全国的度量衡.经测量,该铜方升内口(长方体)深1寸,内口长是宽的1.8倍,内口的表面积(不含上底面)为33平方寸,则该铜方升内口的容积为( ).

图1
A.5.4立方寸 B.8立方寸
C.16立方寸 D.16.2立方寸
4.若a∈R+,二项式(ax+1)6的展开式中所有的系数之和为729,则实数a的值为( ).
A.-3 B.-2 C.3 D.2
5.若正六边形ABCDEF是圆O的内接正六边形,则在圆O中任取一点,该点取自正六边形ABCDEF内(含边界)的概率为( ).
6.已知F1,F2是双曲线C的两个焦点,P为C上一点,且∠F1PF2=60°,|PF1|=3|PF2|,则C的离心率为( ).

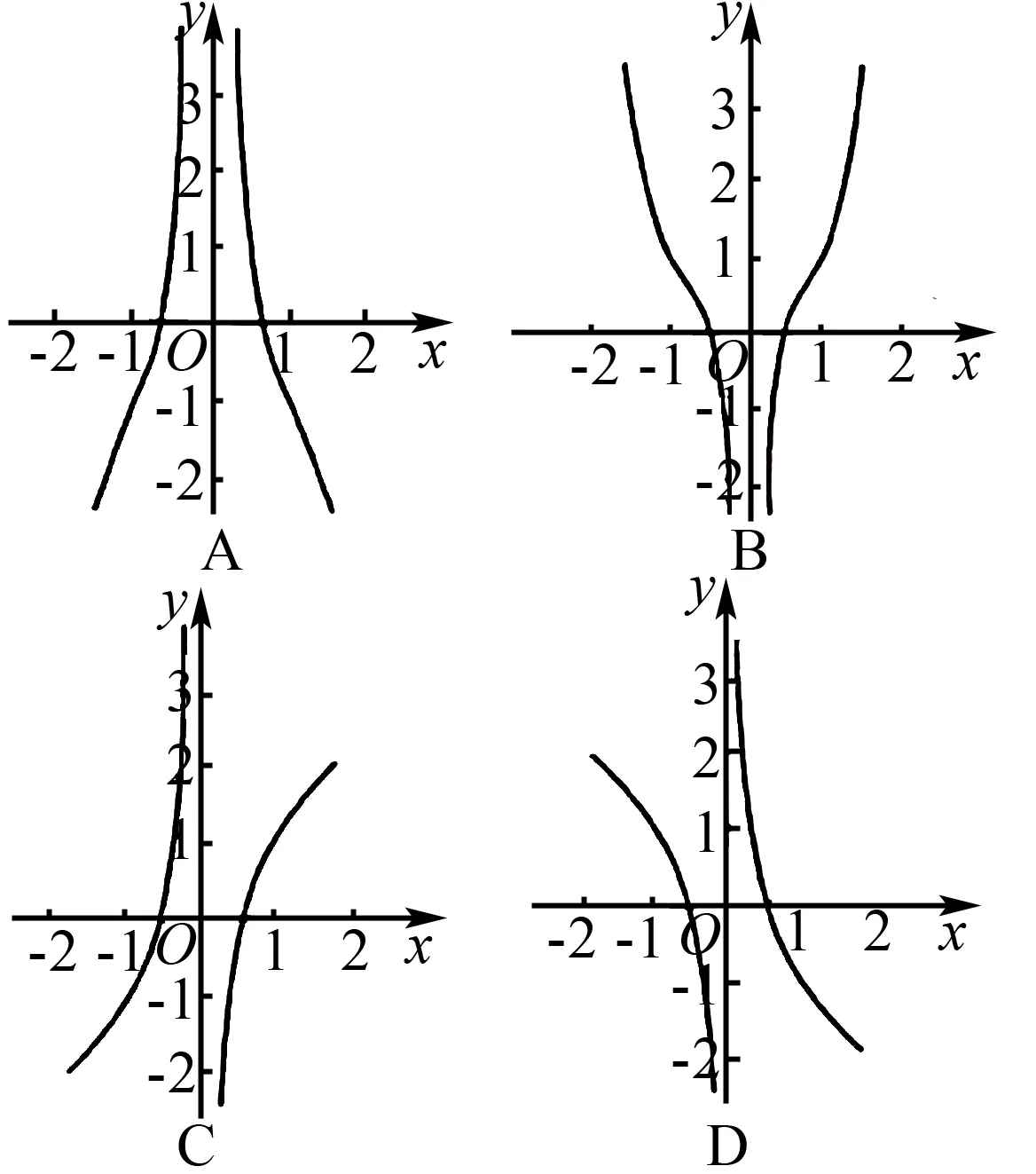
图2
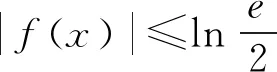
A.(0,ln2] B.(-∞,-ln2]∪[ln2,+∞)
C.(-∞,ln2] D.[-ln2,ln2]

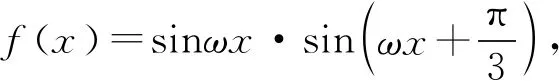
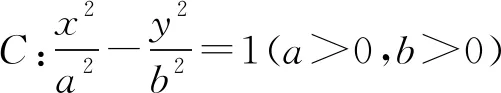
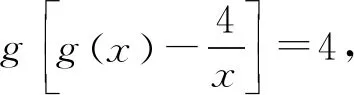
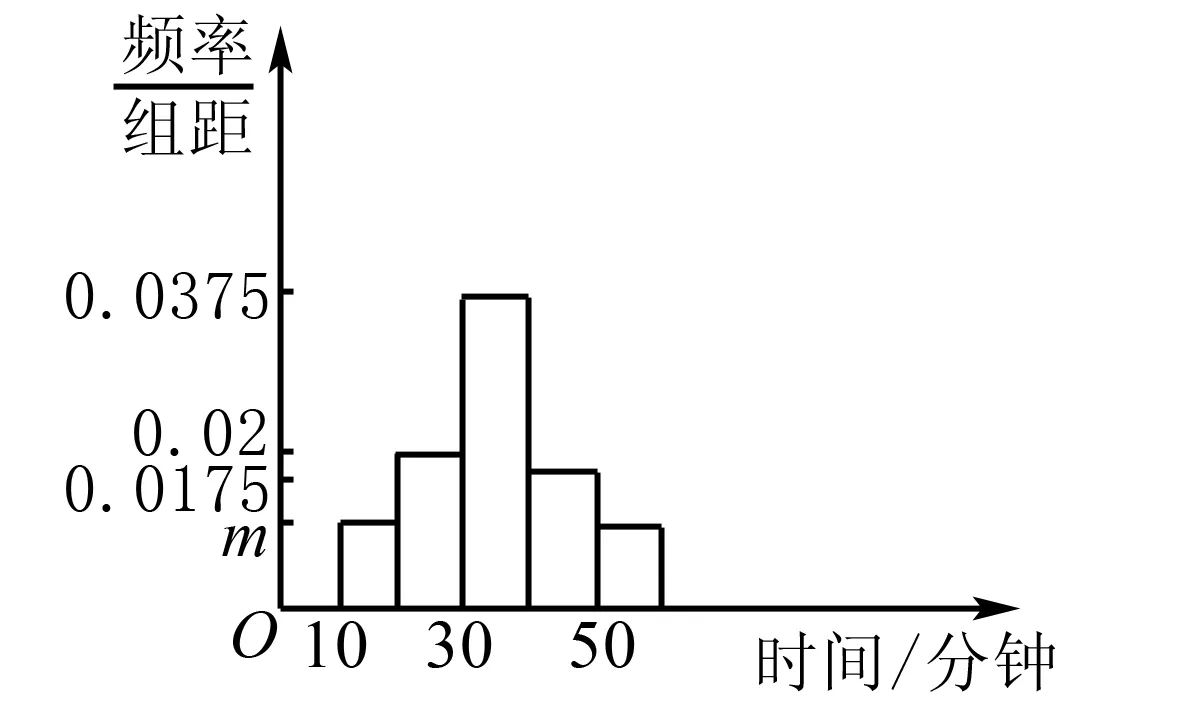
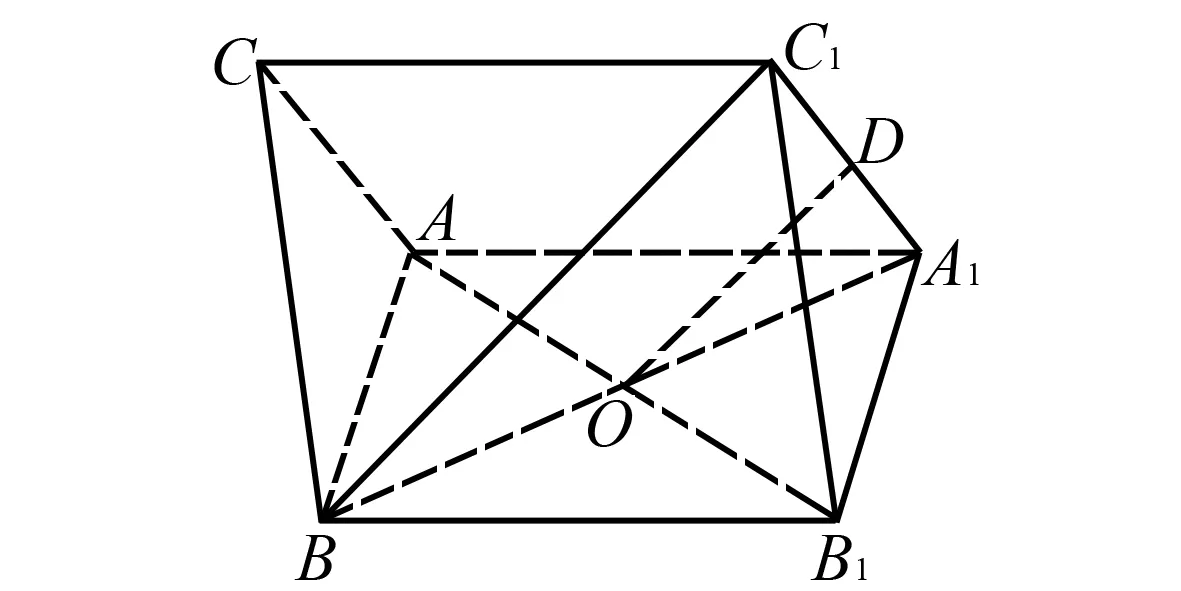
A.g(1)>x1x2B.g(1) C.g(1)=x1x2D.无法比较 16.甲、乙、丙、丁四人玩数字游戏,其中一人进行监督,每人从标有数字1到12的12张卡片中抽取4张. 甲说:我抽到的数字有6和11; 乙说:我抽到的数字有10和12; 丙说:我抽到的数字特别有意思,你们能猜中其中两个吗? 监督员丁看了丙抽到的数字,说:真奇妙,你们三个所抽到的数字之和相等. 从他们的对话,你可以推断丙所抽到的数字中必有两个数字为____. 17.(12分)已知单调递增的等比数列{an}的前n项和为Sn,且满足S5=S3+24,a2a7+a4a5=256. (1)求数列{an}的通项公式; 18.(12分)如图3,三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,AB⊥BB1,BB1=2,O,D分别为棱AB1,A1C1的中点. 图3 (1)求证:OD∥平面BCC1B1; (2)若平面ABC⊥平面ABB1A1,求直线OD与平面AB1C所成的角的正弦值. 19.(12分)某班主任对本班40名同学每天参加课外活动的时间(分钟)进行了详细统计,并绘制成频率分布直方图,如图4所示: 图4 (1)求实数a的值以及参加课外活动时间在[10,20]中的人数; (2)从每天参加活动不少于40分钟的人中任选3人,用X表示参加课外活动不少于50分钟的人数,求X的分布列和数学期望. (1)求椭圆C的方程; (2)若直线l与椭圆C相切,求证:点F1,F2到直线l的距离之积为定值. 21.(12分)已知函数f(x)=x2-4x+4+alnx. (1)讨论f(x)的单调性; (1)求曲线C1的一般方程和曲线C2的直角坐标方程; (2)若点P在曲线C1上,点Q在曲线C2上,求|PQ|的最小值. 23.(本小题满分12分)已知函数f(x)=|2x-a|+|x-a+1|. (1)当a=4时,求解不等式f(x)≥8; 参考答案 1.C.A={x∈Z|x2+2x≤0}={-2,-1,0},则集合A的子集个数为23=8. 4.D.当x=1时,可得二项式展开式中的所有项的系数之和,即(a+1)6=729,所以a+1=±3,解得a=2或a=-4(舍去). 5.B.设正六边形的边长为a,则正六边形的外接圆半径为a,则 14.延长AD到点E,使|AD|=|DE|,则四边形ABEC是平行四边形,由余弦定理知,|AE|2+|BC|2=2(|BA|2+|AC|2),解得|BC|2=14>|AB|2+|AC|2,则△ABC的形状为钝角三角形. 16.由题意知,所有数字之和为78,则甲乙丙三人每人抽到的4个数字之和均为26,则乙抽到的另外两张卡片必为1,3,甲抽到的另外两张卡片为2,7或5,4则丙所抽到的数字必有8,9. 18.(1)连接A1B,则A1B与AB1交于点O.如图5所示,连接BC1.显然四边形ABB1A1为矩形,O,D分别为棱AB1,A1C1的中点,所以OD为△A1BC1的中位线.所以OD∥BC1.而OD⊄平面BCC1B1,BC1⊂平面BCC1B1,所以OD∥平面BCC1B1. 图5 (2)若平面ABC⊥平面ABB1A1,如图6,取AB的中点P,因为△ABC是正三角形,所以CP⊥AB. 图6 因为平面ABC∩平面ABB1A1=AB,所以CP⊂平面ABC,所以CP⊥平面ABB1A1.所以CP⊥PB,CP⊥PO. 19.(1)因为所有小矩形面积之和等于1,所以可得方程10a+0.02×10+0.0375×10+0.0175×10+10a=1,解得a=0.0125,由于参加课外活动时间在[10,20]内的频率等于0.0125×10=0.125,因此参加课外活动时间在[10,20]中的人数为40×0.125=5. X0123P7442144722122 20.(1)曲线|y|=x+1与x轴的交点为(-1,0),所以F1(-1,0),a2-b2=1. 综上可知,可得直线l与椭圆C相切时,点F1,F2到直线l的距离之积为定值1. 21.(1)因为f(x)=x2-4x+4+alnx, 设g(x)=2x2-4x+a,则△=8(2-a). 当a≥2时,△≤0,g(x)≥0,f′(x)≥0,故f(x)在(0,+∞)上单调递增; 当cosθ=1时,|PO|min=3. 所以|PQ|的最小值3-1=2. 23.(1)当a=4时,f(x)=|2x-4|+|x-3|. 当x≥3时,2x-4+x-3≥8,解得x≥5; 当2 综上可得,a的范围为[-2,1].二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)

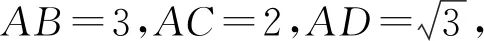
三、简答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤,第17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.)