基于“三个理解”的初中数学探究能力培养策略

黄秋芳

(江苏省苏州工业园区斜塘学校 215024)

初中数学是一门逻辑性与思维性兼备的学科，在课程教学中增强学生对知识技能的探究能力，发展学生解决问题思维能力，是教育教学活动的主要目标.初中数学教师应该在教学过程中革新教学理念，立足于初中学生学习成长的特点，给学生设计高效的学习方案.而发散性思维便于延伸学生学习思路，培养学生灵动的思维方式，学生在不断地探究与分析中掌握举一反三的技能，实现学生多个维度学习与运用知识点.结合张建跃提出的“三个理解”教学理念，谈谈如何在初中数学教学中培养学生探究能力.

1 初中数学教学中培养学生探究能力的前提条件

针对“三个理解”，也就是理解数学、理解学生和理解教学，在培养学生探究能力过程中，教师立足于“三个理解”的思想理念，针对性地设计教学环节与教学内容，将“三个理解”的教学理念融入初中数学课堂教学中，全面提升数学教学质量.

1.1 理解数学

在课堂教学中，理解数学是数学学科教学活动的基础，教师以理解数学目标，掌握数学知识的产生背景，确切的挖掘数学知识概念、数学知识定理和数学知识法则，深度探索数学知识的思想方法，理解各知识点的多元化管理.感悟数学知识的内涵与理性精神，区分核心知识与非核心知识，切合实际的归纳知识生成背景，还要思考是否能够利用和类比以及推广数学知识.

1.2 理解学生

学生是学习的主人，需要在自主学习过程中不断提升自己.初中学生学习是相对活跃的个性化成长过程，积极研究和动手实践均是数学课堂学习的主要方式.给学生提供充分的时间去猜测、计算以及验证，学生认真思考总结知识产生规律，这些均需要建立在教师精心设计教学活动基础之上，由此发展学生知识技能与情感态度价值观.

1.3 理解教学

教学活动的本质是师生交流互动以及共同发展的一个过程，良好的教学活动，应该是教师教和学生学之间的和谐统一.学生是课堂学习的主体，教师通过发挥自身组织者、引导者职能开展教学活动，要调动学生学习兴趣，激发学生主观能动性，带领学生积极思考、乐于探索、勇于创造.让学生潜移默化地掌握科学的学习方法，从而促进学生良好学习习惯的养成.在课堂教学实践中强调学习内容之间的关系挖掘，通过学习探究活动，带领学生经历知识发生与发展的过程，系统地构建数学知识结构体系，丰富学生学习经验.基于此，初中数学就是认真掌握理解数学、理解学生和理解教学的关系，落实学生探究能力的培养.

2 初中数学教学中培养学生探究能力的策略

目前，依旧存在诸多学生过度关注卷面成绩，追求高分数学的错误的学习思想，通过刷题方式，提高学习成绩，把考试当作自身学习的终极目标.大量的课业负担影响着学生探究习惯的养成，长时间之后会降低学生探究热情，无法培养学生的综合能力.目前的初中数学教学中，学生探究能力培养依旧需要进一步探索，要为学生健康成长与个性发展提供有利条件.

2.1 树立学生探究意识，积极正确引导

在培养学生探究能力过程中，就要意识到探究能力的培养并不是盲目探究，而是有针对性地组织学生参与探究活动.在实际的教学中，首先要引导学生树立正确的探究意识，给学生设置合理的情境，引导学生从中探究，有目的的提出解决问题方案，做好培养学生的探究活动的准备.比如在学习“有理数乘方”时，可以设置以下探究活动：一张厚度为1mm的硬纸板对折一次有多厚？对折两次有多厚？对折三次呢？对折10次呢？有人说一张厚度为1mm的硬纸板(足够大)对折24次后，比珠穆朗玛峰还要高，可能吗？这样的问题情境设置，一方面具有悬念，激发学生探究新知的兴趣；另一方面学生能动手操作，便于探究规律.通过教师的有形引导，充分调动学生自主探究意识，便于学生全方位理解数学知识，在数学课堂中得到良好的学习体验.

2.2 实施多元理念，落实因材施教

作为相对独立的个体，学生和学生之间存在显著的个体差异，因此在数学教学活动中，教师应保持客观性与公正性，公平对待每一位学生，不要单一的关注学生学习成绩，更要关注学生综合学习能力的培养.教师也应按照因材施教原则进行教学活动，为学生个性成长提供便捷条件.在学习“用一次函数解决问题”时，设计这样一个问题：一辆慢车和一辆快车沿同一条公路从苏州(A)到无锡(B)，所行的路程y(km)与时间x(h)的函数图像如图1所示．

(1)快车比慢车晚出发____h，慢车比快车晚____h到达B地；

(2)快车经过____h追上慢车，快车行驶了____km追上慢车；

(3)求慢车、快车的速度；

(4)求A、B两地之间的路程；(5)慢车出发多少小时两车恰好相距46km？

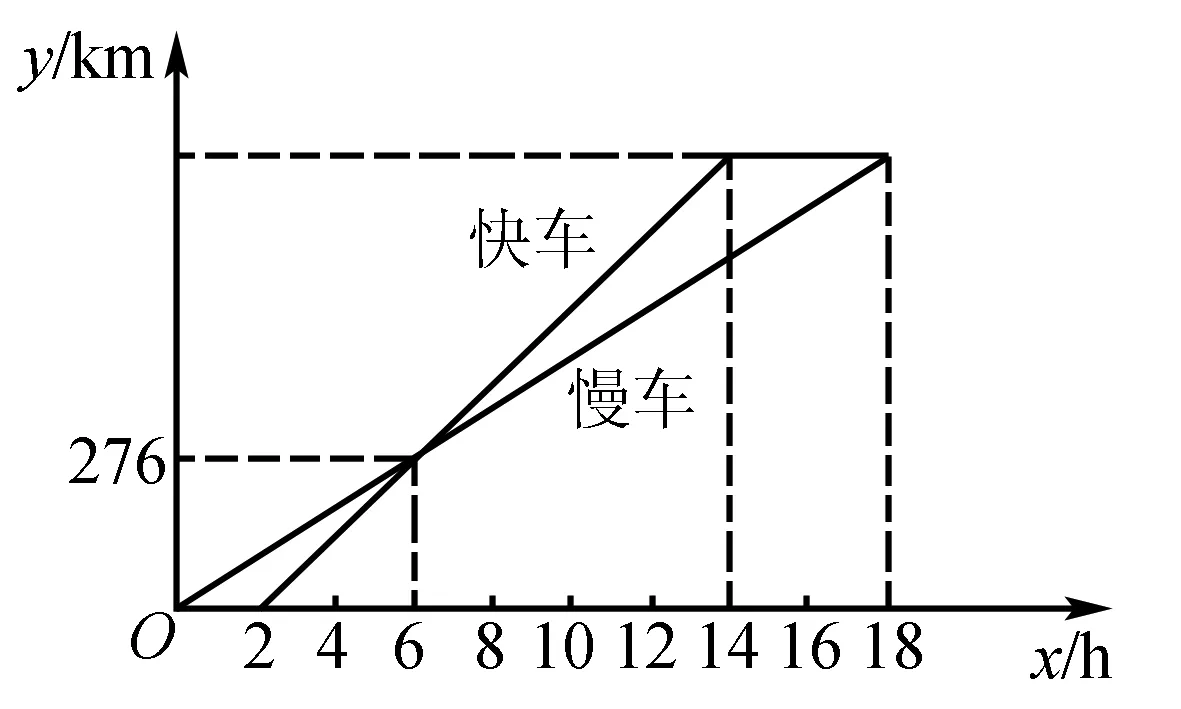
图1

为了让每一位学生按需学习，让不同的学生在数学上获得不同的发展，前四小题是基础题，可以帮助学生深化基础知识内涵.对于学有余力的学生增加第5小题加以拓展，让这部分学生不断地发挥自我潜能，完成探究学习任务.

2.3 激发学生学习兴趣，增强探究欲望

教师应该关注学生学习兴趣的激发，把学习兴趣的培养，当作学生学习效率提升的关键手段，集中学生学习注意力，能够引导学生全方位了解数学知识，生成探究心理.教师需要做好充分的教学准备，课堂上激发学生学习热情，在课后注重教学与学习巩固之间的过渡，实现初中学生深层次学习.比如在学习“勾股定理”时，设置如下问题情境：如图2，两个边长不同的正方形连在一起，请你剪两剪刀，再把所得图形拼成一个正方形.

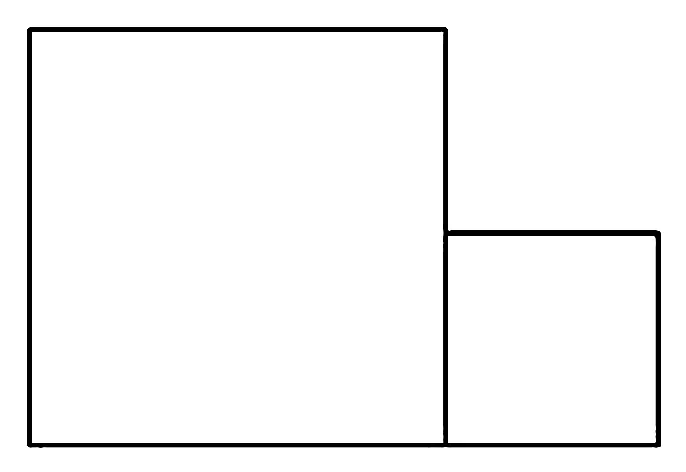
图2

通过这样的问题情境，为学生提供了一个有趣而又富有挑战的问题，激发学生学习本节内容的兴趣，提高了学生自主探究的热情.学生带着问题学习本节课的内容，又用本节课的知识解决此问题，让学生领悟到探究的乐趣，品味到成功的快乐.同时此问题又是证明勾股定理的方法，为下节课勾股定理的证明做铺垫.

2.4 变式延伸，发展学生思维能力

在教学中，一些问题看上去不同，但究其本质却相同，解题思路和方法一致，教师在平时的教学中要注意积累，引导学生加以比较，并且寻找此类问题之间的内在联系，从而寻求通法通解.变式延伸，不但可以解决一个问题，而且可以解决一类问题，避免“题海战术”的同时，也拓宽了学生思维广度，增强了学生的探索意识，发展了学生的思维能力，实现“以少胜多”.比如研究“圆外一点与圆上一点的距离最值”时，设计了以下习题：

例如,如图3，已知边长为2的正方形ABCD，圆O是以AB为直径的圆，G是圆O上的一个动点，连接CG，求CG长的最小值.

图3

变式1如图4，已知边长为2的正方形ABCD，E、F分别是边BC、CD上的点，BE=CF，AE、BF相交于点G，求CG的最小值.

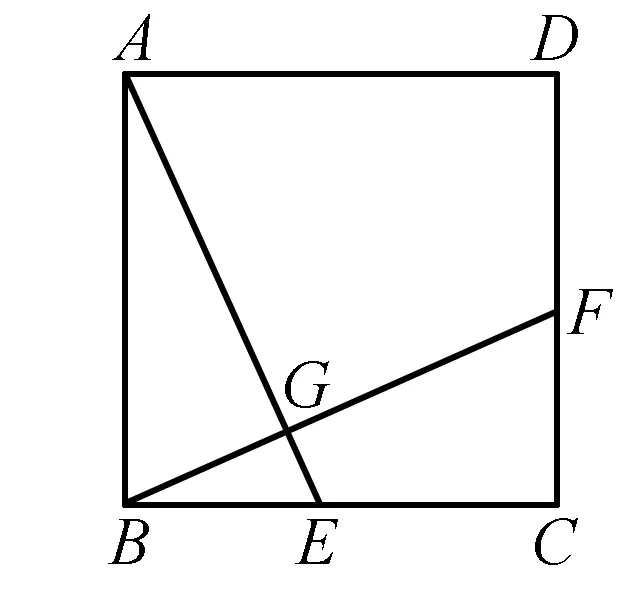
图4

变式2如图5，在Rt△ABC中，∠ABC=90°，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，求线段CP长的最小值.

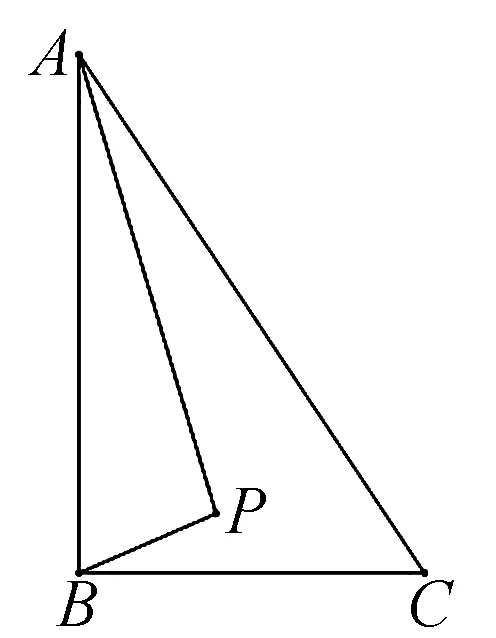
图5

将问题进行迁移变式，逐步探究圆外一点与圆上一点的距离最值，有利于学生解题思想方法的形成和巩固，达到了理解掌握该问题的目的.通过变式延伸，让学生触类旁通，在提高学习效率的基础上，开拓了学生思维的深度和广度，培养了思维的灵活性和变通性.

综上所述，初中数学是一门抽象性与逻辑性相结合的学科，对学生探究能力的培养尤为重要.新课改标准下，数学教师应关注学生的探究能力的提升，通过小组合作与多元化的教学思想，潜移默化地树立学生探究意识，调动学生学习热情，鼓励学生及时进行课后总结和反思，整理完整的数学知识结构.采取高效的措施，如树立学生探究意识，积极正确引导；实施多元理念，落实因材施教；激发学生学习兴趣，增强探究欲望；关注合作探究，发展学生探究能力；变式延伸，发展学生思维能力，鼓励学生在今后的学习中勇于面对困难，积极进取，强化学生数学学习能力与核心素养.