桥梁支座橡胶材料的静态黏弹性本构模型

彭龙帆

(中国建筑第二工程局有限公司华东公司 上海 200135)

橡胶类材料因其优越的弹性和阻尼性能而在各种工程应用中得到了广泛的应用[1-2]，但其黏弹性是工程设计和抗振系统应用中不可回避的问题。静态黏弹性主要表现为蠕变和松弛。当施加恒定荷载时，橡胶的挠度随时间增加而增加，称为蠕变。另一方面，当橡胶保持恒定变形时，应力随时间减小，称为应力松弛。

长期蠕变或松弛实验代价昂贵且耗时，采用时间温度叠加原理(TTSP)从短时间蠕变或松弛实验构建主蠕变或松弛曲线[3-4]。吕慧杰等[5-6]根据AC-13C沥青混合料在5种不同温度下的单轴压缩蠕变试验结果,利用时温等效原理得到沥青混合料的蠕变柔量主曲线，根据松弛模量和蠕变柔量在频率域内的关系确定松弛模量参数，表征更广时间和温度范围内的沥青混合料松弛性质；胡旅洋等[7]在沥青混合料各向异性的研究中,基于2个方向的主曲线绘制需要采用相同的时温等效因子的前提，绘制出满足时温等效原理的主曲线；冯希金等[8]提出结合Yeoh应变能函数的广义Maxwell黏超弹性模型来描述未硫化橡胶力学行为；周梦雨等[9]基于超弹性模型和并行流变模型(PRF)描述了橡胶材料的非线性黏弹性响应特征。

本文利用应力加速原理进行拉伸蠕变试验，以期得到长时间的蠕变曲线；通过拟合得到广义开尔文模型用以表征橡胶材料的黏弹性特性，并进行相应的有限元计算，验证本构模型在橡胶压缩性能的适用性。

1 黏弹性本构模型

1.1 试验材料与结果

橡胶材料由河北衡水东欣橡胶厂提供，橡胶单轴拉伸采用的是长条形矩形试样，长条形矩形试样的尺寸为35 mm×5 mm×5 mm，其中拉伸试验部分为25 mm，上、下两端的5 mm用于夹具加持试件，压缩式样尺寸为直径×厚度=10 mm×10 mm的圆柱体，实验试样见图1。

图1 实验试样

拉伸蠕变和压缩蠕变、松弛试验均在电子万能材料试验机INSTRON 5943上进行。

橡胶单轴拉伸蠕变和压缩蠕变、松弛试验在室温(23 ℃)下进行，在试验开始前需对橡胶进行反复多次的拉伸或压缩以消除橡胶的Mullins效应。拉伸蠕变分别施加4级应力于试件：σ=1.245，1.66，2.07，2.49 MPa，持荷时间为3 600 s。为了消除荷载产生的惯性效应，选取30 s作为蠕变试验的起始点，拉伸蠕变试验结果见图2。

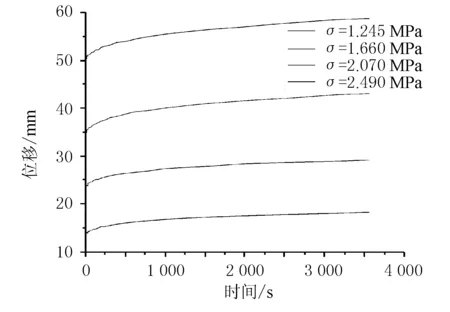
图2 不同应力下的蠕变试验曲线

由图2可见，位移的变化随着时间的增长逐步放缓，在相同时间段内，最开始的时候位移变化量最大，随着时间越长，位移变化量开始慢慢减少；同时，应力大小对位移的变化也有非常明显的效应，应力越大的曲线，位移变化越明显，当时间达到3 500 s时，应力为2.49 MPa的曲线斜率明显大于其他3个应力水平下的曲线斜率，并且曲线斜率随着应力水平的增大而增大，换言之，越大的应力产生的蠕变需要更长时间才能达到收敛状态。

与拉伸蠕变相似，橡胶压缩的蠕变和松弛试验同样在室温条件下进行，持续时间为3 600 s。压缩蠕变试验在应力σ=0.88 MPa下进行，压缩松弛试验在应变ε=10%下进行。压缩蠕变和松弛试验时间均选取600 s为数据起始，试验结果见图3、图4。

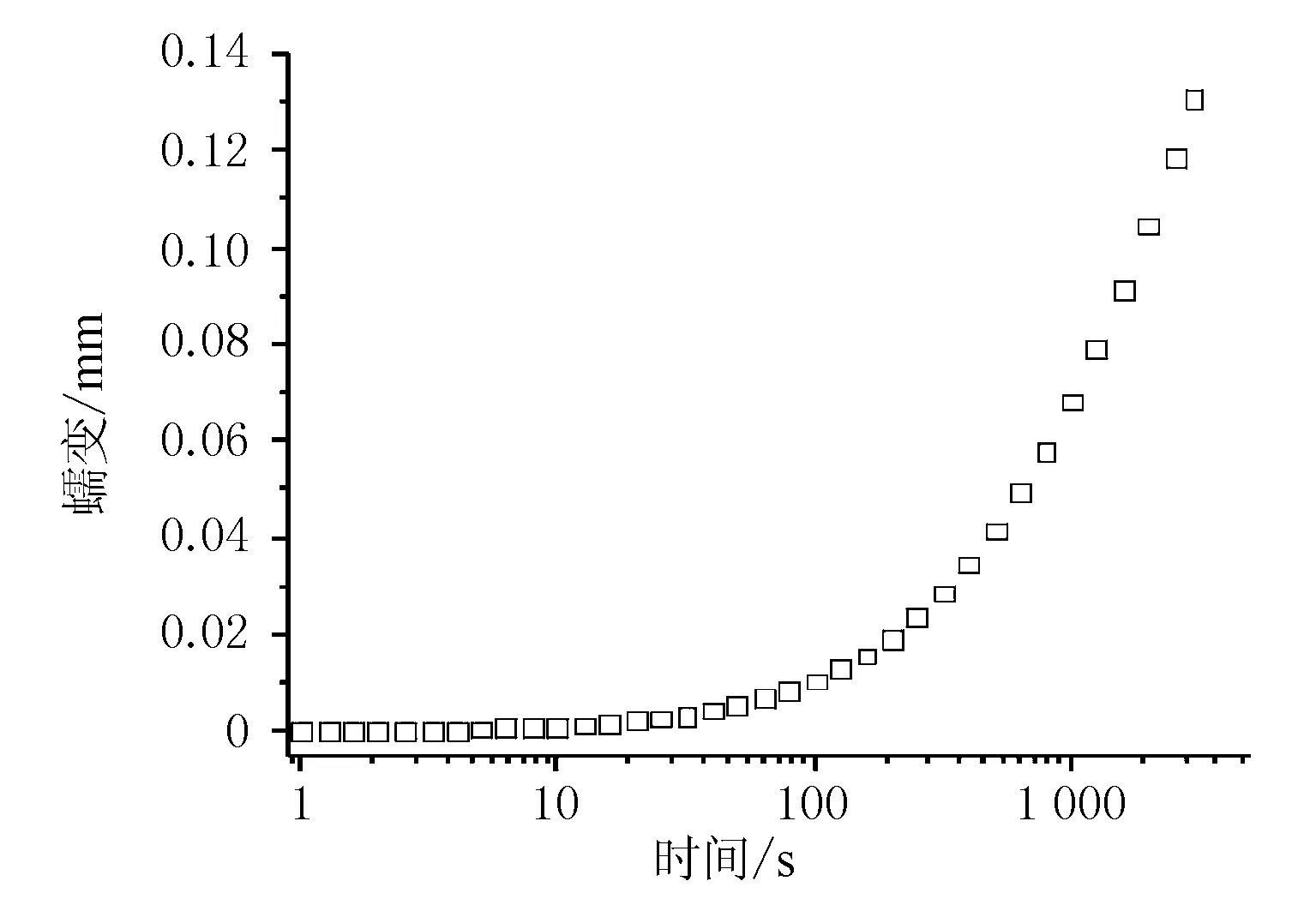
图3 压缩蠕变试验结果(σ=0.88 MPa)

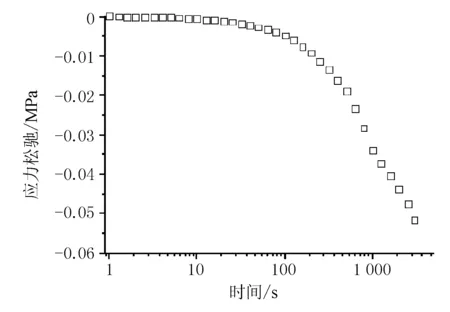
图4 压缩松弛试验结果(ε=10%)

由图3和图4可见，松弛曲线与蠕变曲线互为逆像，这也表明了蠕变和松弛表现出相似的力学特性。在蠕变曲线中，位移随着时间的增大而不断增大，在松弛曲线中，应力随着时间增大而减小。

对图2中的数据进行处理，得到如图5所示的蠕变柔量曲线。其中横坐标，以对数形式表示，以方便后续对蠕变柔量曲线进行平移。

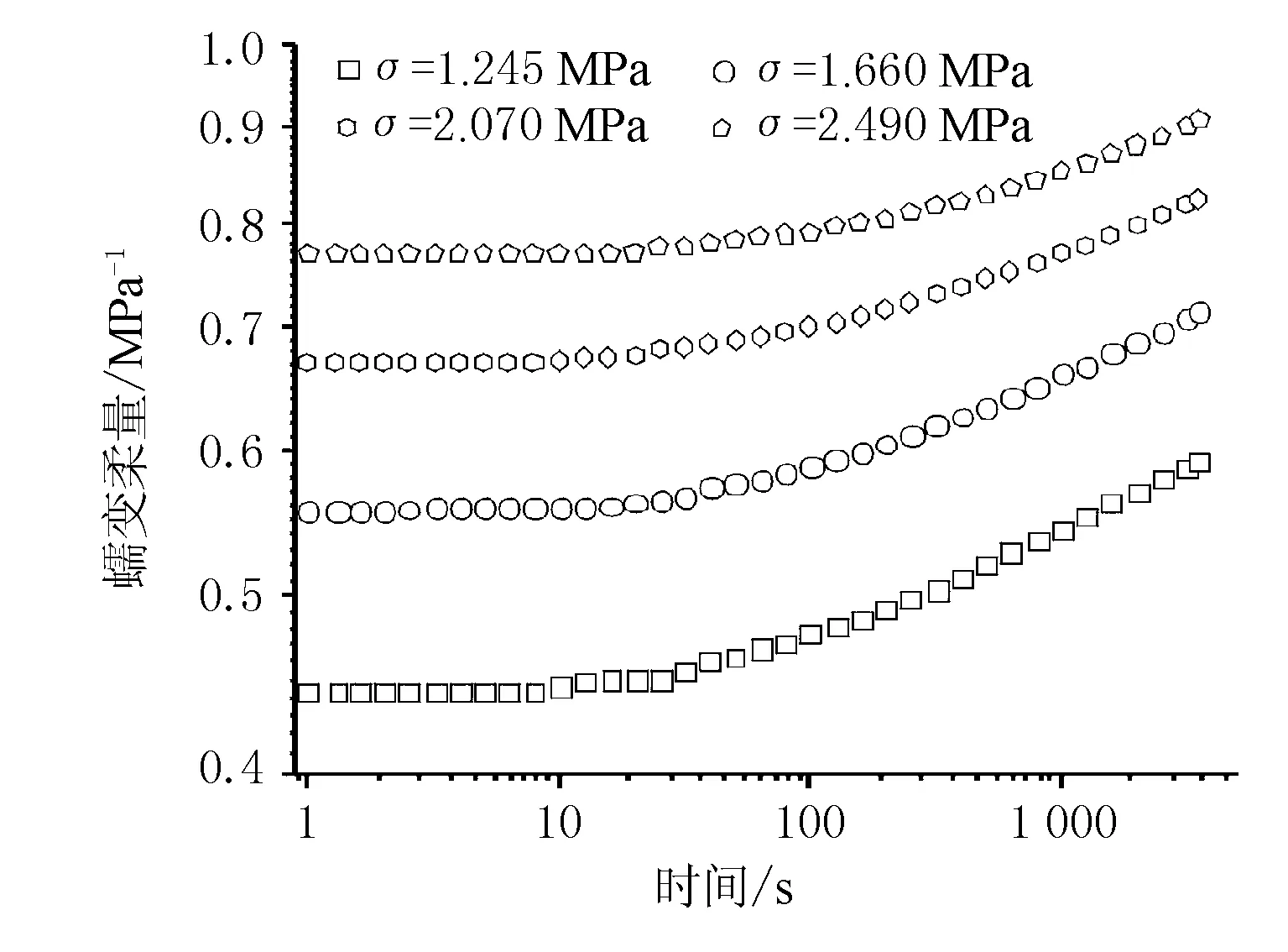
图5 不同应力下的蠕变柔量曲线

1.2 黏弹性模型参数拟合

类似WLF方程，TTSSP可以将短时蠕变进行平移从而得到长期蠕变的数据。当试验温度为恒定时，TTSSP可以缩减成为TTSP，即应力加速原理，其表达式为

(1)

式中：C1和C3为材料参数；φσ为应力平移因子。

选取σ=1.245 MPa为参数应力，对图5中其他应力下的蠕变柔量曲线进行平移，平移的距离即为应力平移因子，其中蠕变柔量和时间轴线均采用对数形式表示。图6为平移结果。

图6 σ=1.245 MPa下蠕变柔量主曲线

由图6可见，平移之后时间跨度明显增大，从试验的3 600 s达到了1.24×107s ，时间跨度提升了4个数量级。换言之，短期蠕变试验可以用来预测长期蠕变的结果，说明应力加速可以作为蠕变加速的有效手段。

应力平移因子曲线如图7所示，对应力平移因子使用最小二乘法，可得到材料参数C1和C3的数值，列于表1。

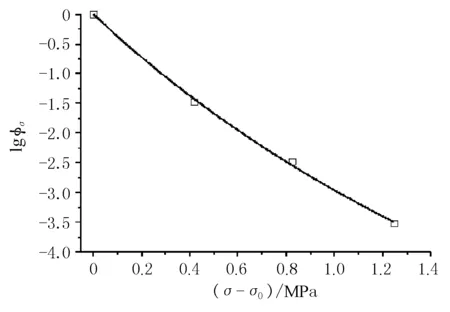
图7 应力平移因子曲线

橡胶的黏弹特性可以使用广义Maxwell模型或者广义开尔文模型来描述，其表达形式均与Prony级数类似。以广义开尔文模型为例，将多个开尔文模型并联，分别表示瞬时弹性、不同弛豫时间的延迟弹性或者不同松弛时间的应力松弛，总应变为各单项开尔文模型的蠕变应变之和，恒应力下的蠕变应变为

(2)

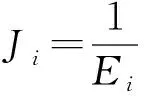
将图6中的数据转化为相对蠕变柔量后输入到有限元中即可得到黏弹性模型本构方程所需参数(见表1)。由于橡胶的不可压缩性，近似认为Ei=3Gi。

表1 黏弹性模型参数拟合

2 数值模拟

在有限元软件建立长条状矩形试件，一端施加位移荷载，另一端给予固定约束。试件的几何形状被离散成8节点六面体的混合单元(C3D8H)，单元尺寸为1 mm，共350个单元；模型见图8。

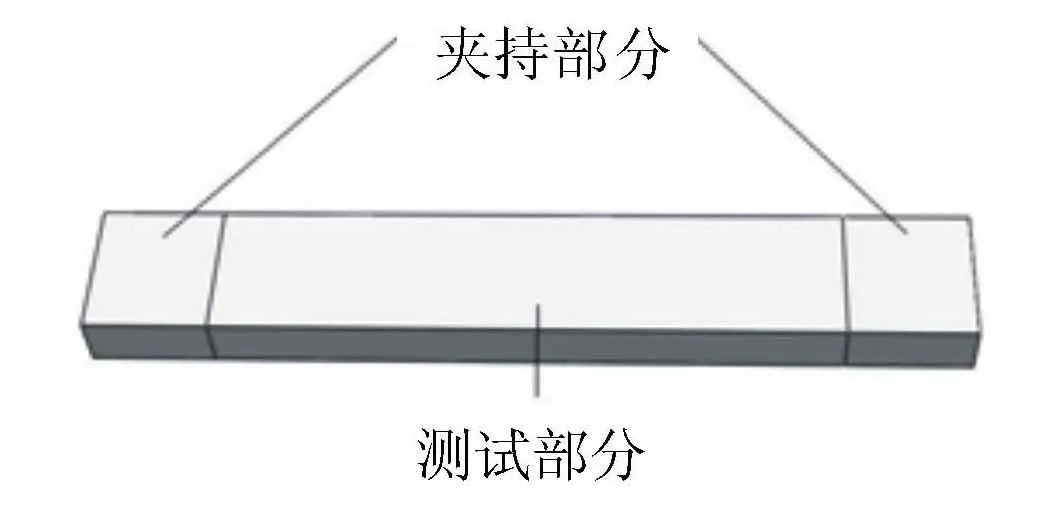
图8 单轴拉伸试样有限元模型

图9展示了在应力σ=1.245 MPa下，橡胶试件随时间的蠕变位移计算结果与试验结果的对比。

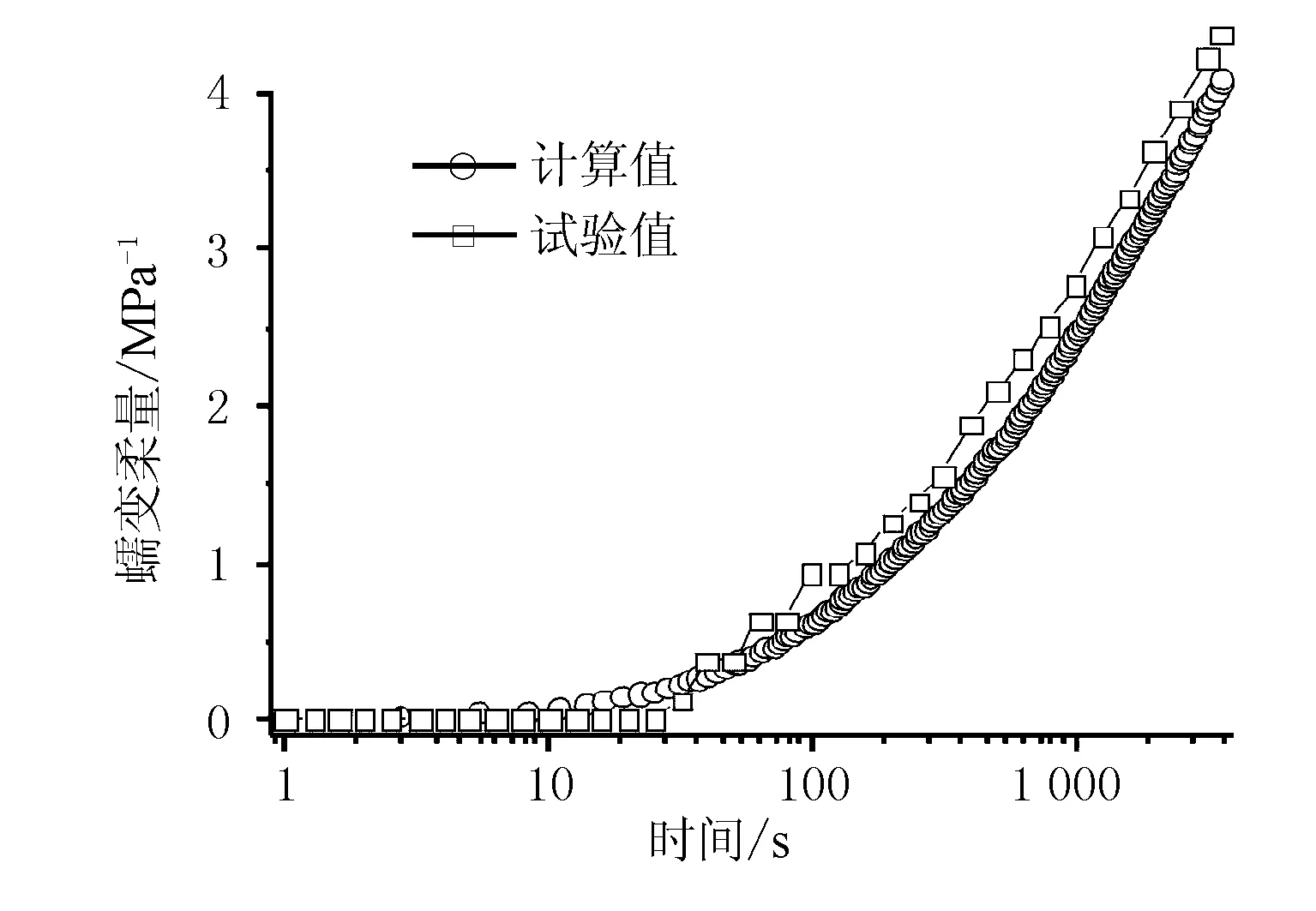
图9 计算结果与试验结果

由图9可见，拉伸蠕变的试验结果由于是以试验开始后30 s的时间点作为蠕变数据的起始点，蠕变处于较稳定状态，因此试件在较短试件段内的蠕变变化并不大，但是蠕变计算的整体趋势和蠕变试验保持一致，且数值接近，因此可以认为所建立的黏弹性作为橡胶的静态本构关系是可行的。

对于圆柱形压缩模拟，基于试件的几何形状和受力特点，按照轴对称问题进行建模分析，用1条直线代表压头底面，并在直线上建立参考点，所有荷载均通过参考点进行加载，单元尺寸为0.5 mm，一共200个单元，单元采用CAX4H，模型见图10。

图10 单轴压缩试件有限元模型

对橡胶压缩试件的蠕变和松弛试验进行仿真模拟，在参考点上分别施加0.88 MPa的应力和10%的压缩应变，持荷时间3 600 s。计算结果见图11、图12。

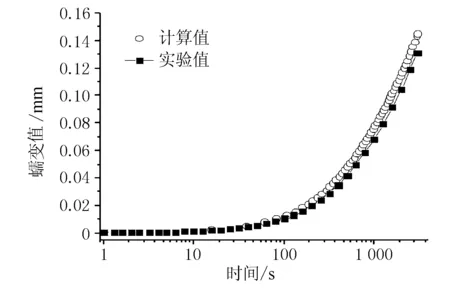
图11 压缩蠕变计算结果

通过对比图11、12计算结果和试验数据，可以看出计算值与试验值较为吻合，验证了建立的本构模型的可行性和适用性；同时，对工程应用有一定的指导意义，即可以通过使用等效原理，由短期的拉伸蠕变得到长期的拉伸蠕变曲线，获取相应本构模型的参数，进而用于求解长期的压缩蠕变和松弛。

3 结论

从橡胶材料的静态角度出发，对橡胶进行单轴拉伸蠕变、压缩蠕变和松弛试验，通过对试验数据的理论分析对本构模型进行研究。利用应力加速原理进行蠕变试验，得到长时间的蠕变曲线，并由有限元软件得到松弛模量和松弛时间参数；最后，对拉伸蠕变、压缩蠕变和松弛进行有限元分析，通过与试验数据的对比，验证本构模型的可行性。