现浇箱梁施工方案满堂支架设计验算方法的探讨

侯孝振

(安徽省路港工程有限责任公司，安徽 合肥 230022)

0 前 言

公路桥梁中现浇箱梁是最为常用的结构形式，现浇箱梁施工方法中有支架法、悬浇法等，其中满堂支架支模施工方案是现浇箱梁施工中较为常见的一种施工方法[1]。满堂支架法施工具有灵活、经济、适应性强等优点，然而鉴于模板支架操作面上施工人员较多，安全性极为重要，支架的承载力及稳定性直接影响着施工安全及箱梁的质量[2-4]。如何较为准确进行支架受力分析是十分必要的。当前项目部现浇箱梁满堂支架施工专项方案验算方法主要有两种常用计算方法：①MIDAS Civil有限元计算；②理论解析计算。本文通过某项目满堂支架两种方法验算结果对比，总结一定经验，为类似工程施工方案设计验算提供一定参考。

1 工程概况

某匝道桥共四联：7×20 m+(30+42+30)m+4×20 m+3×20 m；上部结构主桥采用预应力(后张)连续现浇箱梁，引桥采用普通钢筋混凝土现浇箱梁。本次计算取箱梁搭设支架最高10.5 m的42 m跨现浇箱梁跨施工方案复核验算。箱梁底宽14 m，高2.4 m，悬臂长2 m，端部厚0.2 m，根部加厚至0.5 cm，腹板厚0.75/1.0 m，顶板厚度均为0.25 m，底板厚0.22 m。

2 支架布置设计

采用承插型盘扣式满堂支架施工，具体布置为：支架立杆采用Φ60×3.2 mm钢管，材质为Q345B；横杆、斜撑及水平斜杆均采用Φ48×2.5 mm钢管，材质均为Q235B；竖直斜杆采用Φ48×2.5 mm钢管，钢材材质均为Q195；附加斜撑采用Φ48×3.5 mm，材质为Q235B。横杆竖向步距为1.5 m/1.0 m/0.5 m，立杆纵桥向间距为0.6 m/0.9 m；横桥向间距为0.6 m/0.9 m/1.2 m；所有模板均为15 mm厚优质竹胶板，模板下方布置：横桥向12 cm×12 cm的方木，方木下为纵向(间距同立杆间距)普通10号槽钢；支架布置见图1。基础采用22 cm厚C20素混凝土，基底持力层为经地基处理后满足承载力及正常使用要求土层。

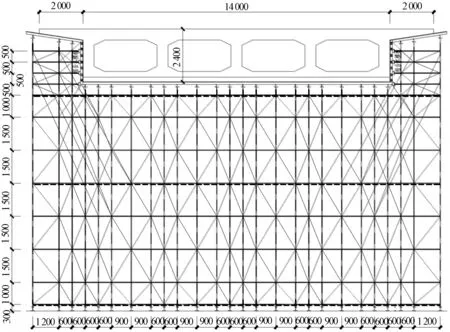
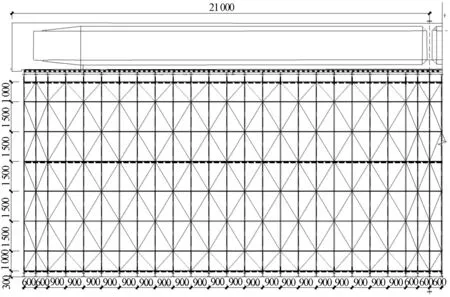
图1 支架布置示意图

3 荷载取值

根据本工程概况及箱梁施工特点，支架验算主要考虑如下荷载：①体系自重q1；②新浇混凝土自重q2(钢筋混凝土容重取γ=26 kN/m3)；③施工荷载(施工人员、机具、材料等)q3=2.5 kN/m2；④振捣混凝土时对水平模板产生的竖向荷载q4=2.0 kN/m2；⑤振捣混凝土时对垂直模板产生的水平荷载q5=4.0 kN/m2；⑥倾倒混凝土作用于模板的产生的竖向荷载q6=2.0 kN/m2；⑦q7箱梁分两次浇筑，第一次浇筑至腹板倒角下方，最大浇筑高度2.4-0.5=1.9 m，本次计算考虑浇筑速度的不确定，取新浇筑混凝土有效压头高度即为最大浇筑高度1.9 m；⑧顺桥向风载计算取按照0.35 kN/m2，横桥向风载计算取0.7 kN/m2；⑨内模荷载q9=2.0 kN/m2。

荷载组合参照路桥施工计算手册执行，其中荷载分项系数取值执行《建筑结构可靠性设计统一标准》(GB 50068—2018)。

4 有限元建模及边界条件设置

支架、方木等采用梁单元模拟，模板采用板单元模拟，立杆底部约束3个方向平动自由度，立杆顶部与10号槽钢、10号槽钢与横向木方、方木与模板均采用弹性连接方式，依据《建筑施工临时支撑结构技术规范》(JGJ 300—2013)输入节点转动刚度。采用MIDAS Civil 2019建立现浇梁支架整体模型，如图2所示。

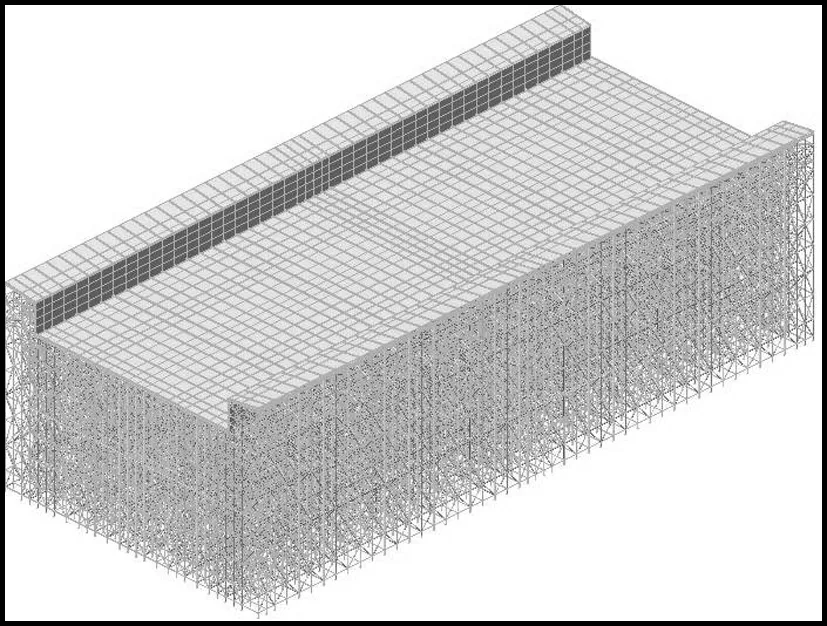
图2 满堂支架有限元模型

5 支架结构受力分析

根据荷载条件及材料特性取值，采用MIDAS Civil根据建立的整体支架模型并输入相应荷载工况分析验算。考虑翼缘板荷载较小，取主箱梁区域支架作为分析对象。

5.1 底模板(t=15 mm)强度验算

由图3知主箱梁区域竹胶板最大组合应力σmax=1.12 MPa。取有限元计算组合应力相对应最大值位置(即支座实腹位置)进行模板理论解析，方木间距150 mm，混凝土高度2.4 m，采用15 mm厚模板，取1 000 mm宽度，跨度按照150 mm，按简之进行计算，模板面荷载设计值q=1.3×(2.4×26+0.5)+1.5×6.5=91.5 kN/m2。最大弯矩设计值Mmax=0.125ql2=0.257 kN·m；最大弯应力设计值σmax=Mmax/W=6.86 MPa。

图3 底模板组合应力云图

5.2 方木强度验算

由图4知方木最大组合应力σmax=1.07 MPa。取有限元计算组合应力相对应最大值位置进行理论解析，方木间距150 mm，跨度为600 mm，按三跨连续梁进行计算，方木线荷载设计值：q=13.73 kN/m，最大弯矩设计值Mmax=0.1ql2=1.11 kN·m，最大弯应力设计值σmax=Mmax/W=6.67 MPa 。

图4 方木组合应力云图

5.3 10号槽钢分配梁强度验算

由图5知10号槽钢最大组合应力σmax=92 MPa。取有限元计算组合应力相对应最大值位置进行理论解析，槽钢间距600 mm，跨度为900 mm，按三跨连续梁进行计算，方木线荷载设计值：q=13.73 kN/m，其中方木传递槽钢为集中力，最大弯矩设计值Mmax=4.4 kN·m，最大弯应力设计值σmax=Mmax/W=110.94 MPa 。

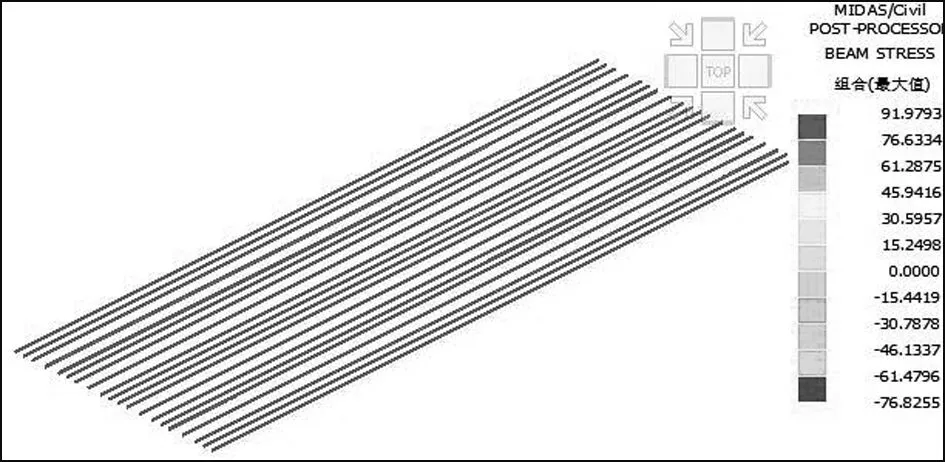
图5 10号槽钢分配梁组合应力云图

5.4 立杆强度验算

由图6知立杆最大压弯组合应力σmax=144.8 MPa。分析取立杆受力最大位置(实心混凝土区域)进行理论解析，计算长度依据盘扣式支架安全规程取lo=1.8 m，立杆稳定系数φ=0.558，不组合风荷载轴力设计值：Nmax=53.6 kN，稳定应力设计值σ=N/(φA)=168.3 MPa。

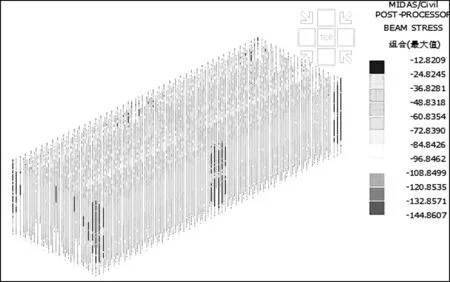
图6 立杆组合应力云图

6 结 语

1)满堂支架有限元计算结果与解析法计算结果进行对比，结果表明有限元计算结果较理论解析结果偏小，其中模板、方木两种算法组合应力结果相差较大，而10号槽钢主楞、立杆两种算法组合应力结果相差较小。

2)两种计算方法计算结果存在偏差，分析原因认为主要有两个方面：①由于MIDAS Civil计算考虑整体性及模板、方木及10号工字钢(或槽钢)相互连接计算边界条件简化所致，随着荷载向下传递边界条件影响减小，故10号槽钢和立杆计算结果相差较小；②依据模板施工安全技术规范的理论解析按构件分开计算，计算模型简化偏保守。

3)鉴于模板支架操作面上施工人员较多，安全性极为重要，为偏安全考虑，特别是对于MIDAS Civil有限元计算结果与容许值接近的方案建议补充理论解析计算。

4)本文研究为类似工程施工方案设计验算提供一定参考，后续针对存在计算误差原因将开展进一步研究。

[ID:013061]