浓度梯度对T型管中爆轰波传播特性的影响
2022-04-26潘剑锋李剑星
姜 超,潘剑锋,李剑星,倪 靖
浓度梯度对T型管中爆轰波传播特性的影响
姜 超,潘剑锋,李剑星,倪 靖
(江苏大学能源与动力工程学院,镇江 212013)
针对爆轰波在浓度梯度作用下衍射、熄爆到再起爆过程,基于开源软件OpenFOAM研究了两种不同混合气在3种不同浓度梯度下流场特征.结果表明:随着浓度梯度增大,横向爆轰波强度会减弱,爆轰波更易解耦.前导激波与浓度梯度相互作用会使爆轰波面发生弯曲,并且改变横向爆轰波和马赫杆的传播过程.对于稳定气体(H2/O2/Ar),爆轰波在管长范围内没有成功起爆;对于不稳定气体(C2H4/O2),爆轰波成功起爆.
浓度梯度;爆轰波;胞格结构;OpenFOAM
爆轰波是一种能够自持传播并且具有强间断的现象,其由前导激波和化学反应耦合组成.波前反应物经过前导冲击波的绝热压缩,在很短时间内释放出巨大能量,被释放的化学能又支撑了前导冲击波向前传播.爆轰波因其具有速度快、燃烧热效率比高等优点在先进推进领域受到广泛关注.另一方面,爆轰在工业领域每年都会引发灾难性后果,如粉尘爆炸、瓦斯爆炸等.在能源与化工领域,碳氢燃料通常采用管道输送.管道中通常存在大量分叉管道,因此研究爆轰波在分叉管道中传播过程对于预防和减小爆轰波危害具有重要作用[1-3].
在过去几十年中,相较于爆轰波在直管道中的起爆和传播特性的研究,对于爆轰波在复杂结构的管道中传播的研究相对较少.Li等[4]通过数值模拟研究发现当爆轰波由小管道进入大管道时,膨胀波会使小管道出口处的爆轰波衰减.激波在大管道壁面反射导致局部热点形成,进而可以提供充足能量实现重新起爆.Wang等[5]研究了爆轰波在90°分叉管道中的重新起爆过程,发现垂直管道中的激波反射会使发生衍射的爆轰波重新起爆,并且反射形成的射流在爆轰波起爆过程扮演重要角色.在另一项研究中,他们发现水平管道中发生马赫反射,而垂直管道中发生规则反射并且规则反射逐渐向马赫反射转变[6].
在众多工业事故中,爆轰波的起爆和传播通常是在不均匀介质中发生的,因此揭示爆轰波在不均匀介质中起爆和传播机制对预防事故发生和减小事故的危害具有重要意义.与爆轰波在均匀混气中起爆和传播相比,火焰加速过程在具有浓度梯度的管道中要更快,更容易引起缓燃向爆轰过程的转变(DDT),并且爆轰波的传播速度要小于均匀混气中理论的CJ爆轰速度[7].由于管道一侧氧化物或稀释气体逐渐占据主要成分,垂直于管道方向的化学诱导时间急剧变化导致前导激波和化学反应前锋解耦,爆轰波面会发生弯曲[8].Vollmer等[9]和Wang等[10]在光滑管道以及带有扰流片管道中施加横向浓度梯度,实验研究了整个DDT过程.Kessler等[11]通过数值模拟研究发现管道中浓度梯度越大,爆轰波传播速度越慢,当浓度梯度足够大时,爆轰波会失效.Ettner等[12-13]使用详细氢氧化学反应机理研究了胞格随浓度梯度的变化趋势,结果表明浓度梯度会使胞格变得更加不规则,同时胞格尺寸增大.
目前仍需深入研究带有浓度梯度介质中爆轰波起爆和传播问题,特别是爆轰波在不均匀混合气中衍射、熄爆到再起爆问题.本文针对2H2/O2/Ar以及C2H4/3O2不均匀混合气,对爆轰波由垂直管道进入带有浓度梯度水平管道后的爆轰波衍射、熄爆等过程进行了模拟研究,揭示爆轰波在带有浓度梯度管道中的流场特征.
1 数值方法与物理模型
1.1 数值方法
本文采用可压缩反应性纳维-斯托克斯(NS)方程,质量、动量、能量和组分守恒方程可以表示为:
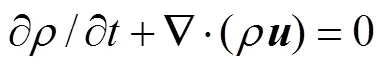


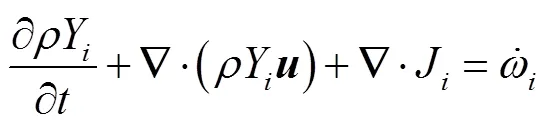
式中:为混合物密度;为速度;为静压;为满足斯托克斯假设的黏性应力;=+0.52-为混合物的总能,为显焓;为燃烧热;Y为组分(=1,…,)的质量分数;为组分的反应速率.此外,J和分别为组分的质量扩散通量以及热通量.详细的模型介绍见文献[14-15].
求解方程组时,时间项采用二阶Crank-Nicolson[16]格式,对流项使用具有二阶精度的KNP[17]格式进行离散.为了减少网格数量和计算量,应用自适应网格功能在计算过程中动态加密和粗化局部网格.模拟采用基于OpenFOAM[18]平台二次开发的求解器DCRFoam,该求解器已经经过验证能够准确模拟爆轰现象[14-15, 19-20].
1.2 物理模型和初始条件
如图1所示,计算区域为一T型管道,水平方向长为230mm,管道内径为30mm.下方管道充满物质的量比为2∶1∶1的H2/O2/Ar以及物质的量比为1∶3的C2H4/O2,初始压力为8kPa,温度为300K.下方管道中有一自下而上自持传播的爆轰波.网格为二维正交网格,网格初始大小为Δ=Δ=0.5mm,采用三级加密,最小的网格尺寸可以达到0.0625mm,该尺寸足以捕捉流场中流动细节以及三波点等特征.上方横向管道中的浓度梯度自下边界到上边界为燃料(H2、C2H4)和O2的线性分布,因此自下而上为从富燃过渡到贫燃状态.管道内壁面边界条件设置为绝热和无滑移,左右端面为出口.

图1 计算区域示意
横向浓度梯度分布如表1所示.算例1~3混合气为H2/O2/Ar,算例4~6混合气为C2H4/O2.由于氢气是组分中扩散性最强的组分,H2的扩散时间尺度大致表示为diff=/0,其中为管道内径,0为H2的扩散系数,爆轰波在管道中传播的时间可以定义为prop=/cj,其中为管道水平方向长度,cj为理论CJ(Chapman-Jouguet)速度.由于diff(约10s)比prop(约10-4s)大5个数量级,所以在爆轰波传播过程中组分之间的扩散效应可以忽略,可以认为浓度梯度保持不变[21].
表1 不同算例横向浓度梯度分布
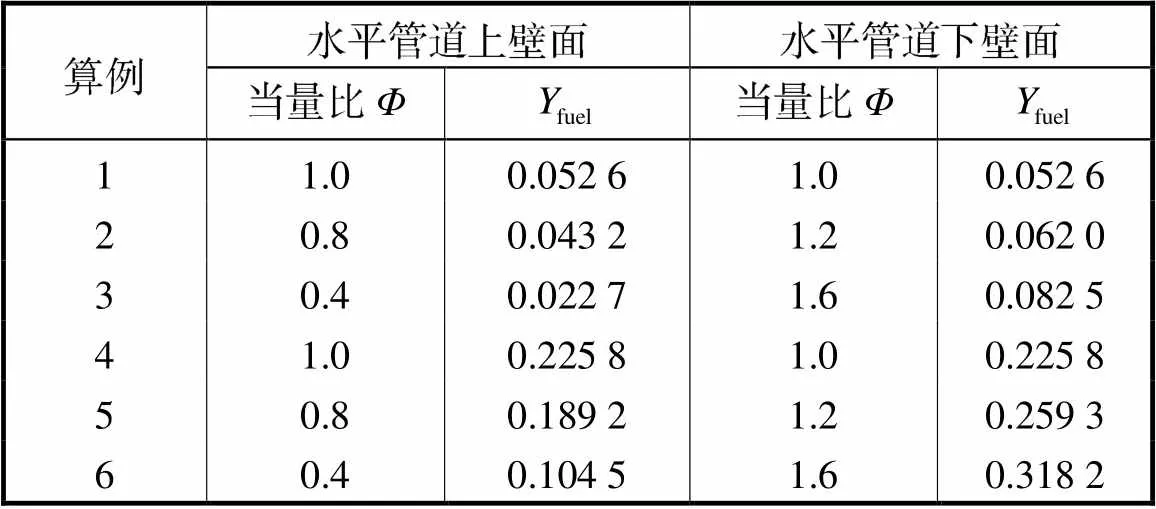
Tab.1 Transverse concentration gradient distribution in different cases
2 结果与讨论
2.1 爆轰波绕射过程的胞格结构
通常稳定自持传播的爆轰波的波阵面并非像一维ZND结构的平面状态,波阵面由一系列马赫杆形成.横波、马赫杆以及入射激波相交形成三波点结构,而三波点的运行轨迹成为爆轰波的胞格结构[22].图2为算例 2胞格结构.爆轰波由T型管中垂直管道进入水平管道,形成网状胞格结构,如图2区域Ⅰ所示.当爆轰波经过垂直拐角,两侧三波结构会逐渐消失.爆轰波撞击水平管道上壁面后,反射激波向两边传播并形成较强的横向爆轰波.随后横向爆轰波撞击下壁面再次发生反射,形成与区域Ⅱ类似的结构.由于管道较短,最终并没有再次形成稳定传播的爆轰波.

图2 计算过程中最大压力轨迹
图3为算例1~6计算过程中最大压力轨迹.从算例1到算例3以及算例4到算例6,水平管道中浓度梯度逐渐增大.对于算例1到算例3,区域Ⅰ的胞格长度逐渐增大,这是由于随着浓度梯度增加,化学反应诱导区长度逐渐增大,化学反应活性降低.位于区域Ⅱ和Ⅲ的烟迹颜色深浅表明随着浓度梯度增大,横向爆轰波的强度减弱.算例1和2位于区域Ⅲ的烟迹中存在不规则的胞格结构,横向爆轰波未解耦.算例3中位于区域Ⅲ的烟迹逐渐变淡,爆轰波彻底熄爆,同时反射波强度与其他两组相比也要弱很多.对于算例4到算例6,由于其混合气属于不稳定气体,因此其胞格相对不规则,其左右两侧并不完全对称.反射形成的横向爆轰波并未像算例1到算例3的横向爆轰波解耦,其能够稳定传播直至撞击壁面.第一次反射后水平管道中有横波产生,随着浓度梯度增大,横波产生的时间提前.第二次反射后,算例4~6没有形成如算例1~3的横向爆轰波.

2.2 浓度梯度对H2/O2/Ar爆轰波面的影响
图4为为110μs、118μs时,算例 2中区域Ⅰ中的温度云图(左)和密度纹影(右).爆轰波经过分叉管道的垂直拐角时,从拐角处散发出稀疏波并与前导激波相互作用,进而使前导激波的强度下降,激波面发生弯曲[5].由于分叉管道面积突然增大,横波不能继续与壁面发生碰撞,导致三波结构消失.在受扰动区域,反应前锋逐渐与前导激波解耦,两者之间存在经过前导激波压缩预热的未燃混合气.由于没有足够化学反应能量的支持,两侧受扰动区域爆轰波逐渐熄爆.前方未受扰动区域,前导激波和化学反应锋面仍然耦合在一起,带有三波结构的爆轰波以原有速度向前传播.
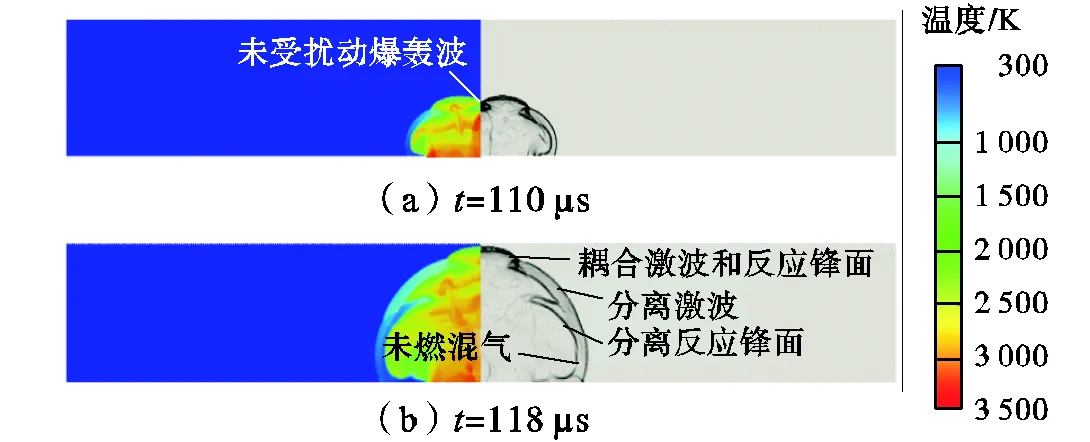
图4 算例2区域Ⅰ温度云图和密度纹影
图5为123~151μs时,算例 2对应于区域Ⅱ中的温度云图(左)和密度纹影(右).爆轰波撞击上壁面发生反射,反射激波主要分为两部分,一部分为非反应性的反射激波,其向T型管竖直部分传播;另一部分为反应性反射激波,反应性反射激波在传播过程中逐渐分为马赫杆以及横向爆轰波,如图5(a)和(b)所示.马赫爆轰波的传播速度比解耦的前导激波快,马赫爆轰波会逐渐超越前导激波.马赫爆轰波向下游传播时,波面会发生弯曲,这是因为管道自上而下存在浓度梯度,即从上到下为贫燃过渡到富燃,爆轰波在不同当量比的可燃混合气中传播速度也不一致.图6为区域Ⅱ不同时刻H2质量分数分布.126μs和128μs时,氢气的质量分数有上升的趋势,这表明前导激波与不均匀的浓度梯度有相互作用的过程,该过程使原来水平方向均匀分布的浓度梯度由当量比接近1向富燃转变,横向爆轰波靠近管道中心一侧缺少充足能量的支持,前导激波和反应锋面逐渐解耦,而外侧仍保持耦合状态,如图5(c)所示.该现象亦可由图2区域Ⅱ中压力最大值烟迹的深浅说明,区域Ⅱ外侧烟迹颜色比内侧深,表明内侧爆轰波逐渐熄爆. 赫爆轰波与横向爆轰波演化过程类似,马赫爆轰波受浓度不均匀分布的影响解耦,其后方包含一团未燃混合气.

图5 算例2区域Ⅱ流场温度云图和密度纹影

图6 算例2区域Ⅱ不同时刻H2质量分数分布
图7为154~175μs时,算例 2对应于区域Ⅲ中的温度云图(左)和密度纹影(右).由马赫爆轰波解耦形成的马赫波撞击下壁面,导致波后压力和温度急剧升高,形成局部热点,如图7(a)所示.第二次反射后,反射激波演化为马赫杆和横向爆轰波,其传播过程类似于区域Ⅱ.图8为算例2区域Ⅲ不同时刻H2质量分数分布,与图6描述的H2质量分数分布相反.在160μs和164μs时,管道水平方向氢气质量分数分布不断下降,水平方向氢气分布由富燃向当量比为1转变.因此横向爆轰波在向上传播过程中,远离管道中心一侧缺少充足化学反应能量的支持,前导激波和反应锋面逐渐解耦,而内侧仍保持耦合状态,如图7(c)所示.马赫杆受浓度梯度的影响,导致反应锋面和前导激波分离.最终,在管长范围内没有形成稳定传播的爆轰波.

图7 算例2区域Ⅲ流场温度云图和密度纹影
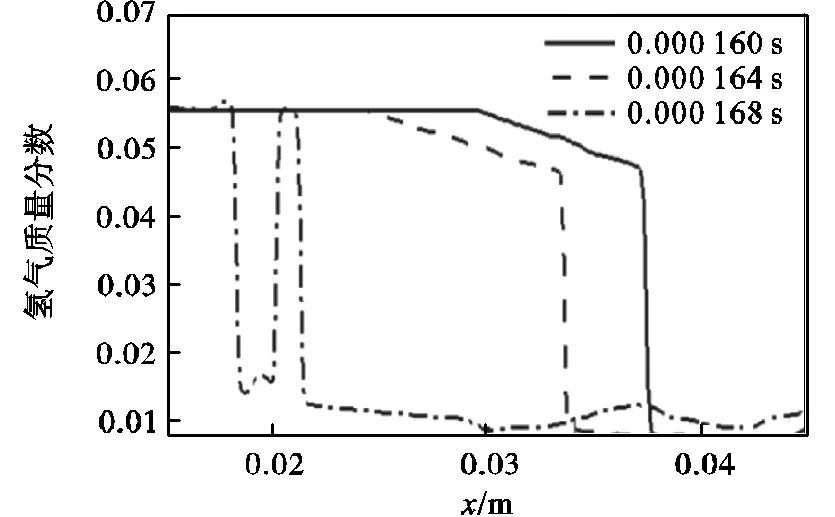
图8 算例2区域Ⅲ不同时刻H2质量分数分布
2.3 浓度梯度对C2H4/O2爆轰波面的影响
图9为算例5中区域Ⅱ和Ⅲ中不同时刻反射过程温度云图.由于不稳定爆轰两侧云图相对不对称,因此两侧图片都为温度云图.爆轰波衍射过程和算例2相似,因此在此不做分析.在=122μs时刻,管道中已经发生第一次反射,形成和算例2相似的结构,包含马赫杆、横向爆轰波以及分离激波等.在=132μs时刻,管道中发生第二次反射.此时的马赫爆轰波并没有解耦,其波面形成多个三波点,这些三波点使马赫爆轰波向能够自持传播的爆轰波转变.由于第一次反射形成的马赫爆轰波未解耦,前导激波后没有未燃气体,因此第二次反射后未形成横向爆轰波,如图9中140μs和148μs时刻.在=154μs时刻,水平管道中已经形成能够稳定传播的爆轰波,这一现象与算例2不相同.

图9 算例5区域Ⅱ和Ⅲ流场温度云图
图10为算例6中区域Ⅱ和Ⅲ中不同时刻反射过程温度云图.在=130μs时刻,管道中已经发生第一次反射,水平管道两侧出现不同的现象.左侧现象和算例5相同,而右侧马赫爆轰波远离右侧马赫杆的一侧出现解耦,这一现象和算例2相同.由前面分析可知,前导激波与浓度梯度之间的相互作用使管道水平方向同样产生浓度梯度.内侧横向爆轰波由于缺少化学反应能量的支持逐渐解耦.在=134μs时刻,左侧的马赫爆轰波没有解耦,其波面形成多个三波点.右侧马赫爆轰波面温度降低,其逐渐解耦,并且此时右侧横向爆轰波也完全解耦.因此经过第二次反射,右侧管道中仍有横向爆轰波形成,如图10中142μs和148μs时刻.在=154μs时刻,水平管道中同样已经形成能够稳定传播的爆轰波.通过对比算例5和6可以发现,当管道中浓度梯度增大时,爆轰波面弯曲程度同样增大,如图9(e)和图10(e).本文下壁面附近为富燃工况而上壁面附近为贫燃工况,爆轰波在本文工况下富燃工况中传播速度要大于在贫燃工况中传播速度.因此下壁面附近爆轰波传播速度更快,导致爆轰波面发生弯曲.
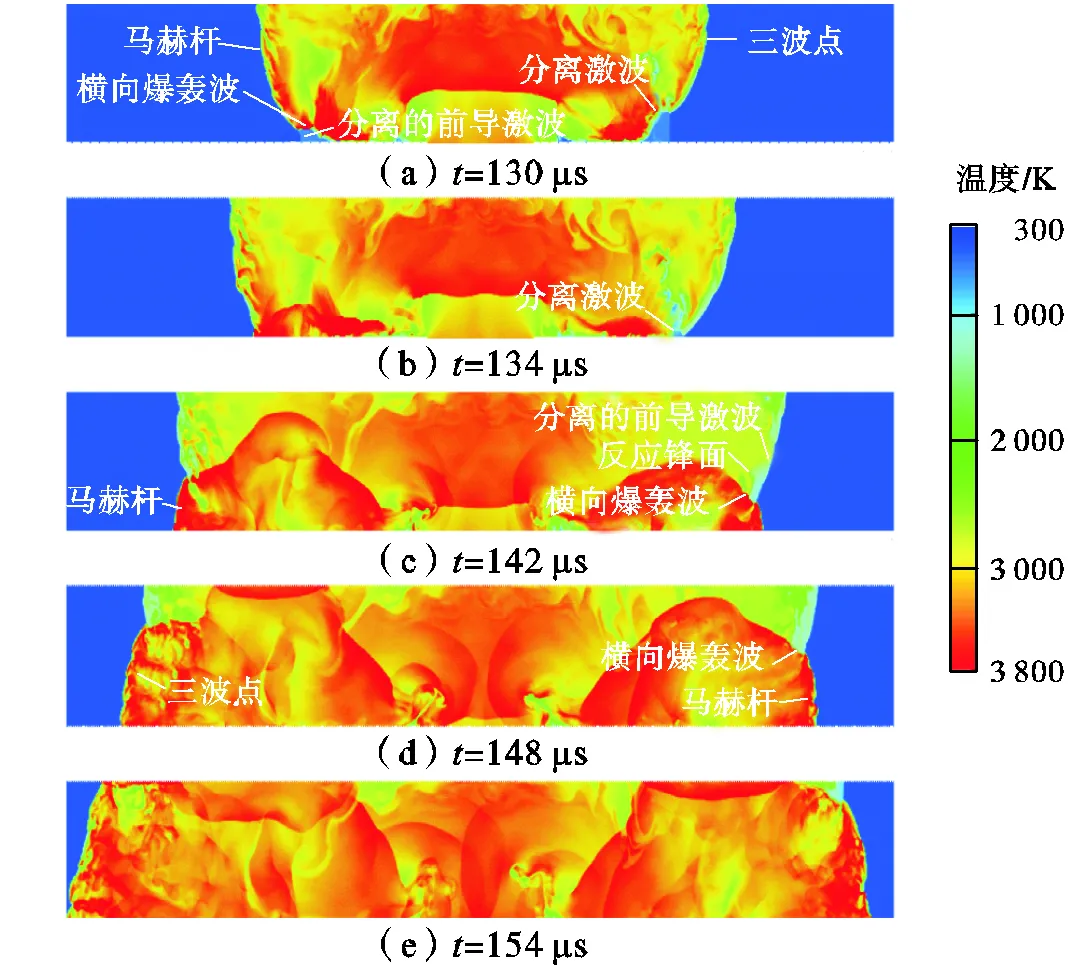
图10 算例6区域Ⅱ和Ⅲ流场温度云图
3 结 论
本文研究了爆轰波在带有浓度梯度的T型管中衍射、熄爆等过程的流场特征,可得到爆轰波在带有浓度梯度管道中传播的如下结论.
(1) 随着浓度梯度增加,横向爆轰波强度会减弱,马赫爆轰波解耦变快.前导激波使区域Ⅱ水平方向浓度梯度由当量比接近1向富燃转变,使区域Ⅲ水平方向浓度梯度由富燃向当量比接近1转变.
(2) 对于H2/O2/Ar混合气,3种浓度梯度下爆轰波在管长范围内都没有成功起爆.两次反射均会形成马赫杆和横向爆轰波,且横向爆轰波受水平浓度梯度影响逐渐解耦.
(3) 对于C2H4/O2混合气,爆轰波在管长范围内成功起爆.第一次反射后马赫杆面会形成新的三波点.随着浓度梯度增大,横向爆轰波和马赫杆会解耦,但是早期形成的三波点会使马赫爆轰波逐渐发展成为能够自持传播的爆轰波.
[1] Wolański P. Detonative propulsion[J].,2013,34(1):125-158.
[2] Lee J H S.[M]. Cam-bridge:Cambridge University Press,2008.
[3] Eichert H,Fischer M. Combustion-related safety aspects of hydrogen in energy applications[J].,1986,11(2):117-124.
[4] Li C P,Kallasanath K. Detonation transmission and transition in channels of different sizes[J].,2000,28(1):603-609.
[5] Wang C J,Xu S L,Guo C M. Gaseous detonation propagation in a bifurcated tube[J].,2008,599:81-110.
[6] Guo C M,Wang C J,Xu S L,et al. Cellular pattern evolution in gaseous detonation diffraction in a 90°-branched channel[J].,2007,148(3):89-99.
[7] Boeck L R,Katzy P,Hasslberger J,et al. The GraVent DDT database[C]// 25(). Leeds,UK,2015.
[8] Lieberman D H,Shepherd J E. Detonation interaction with a diffuse interface and subsequent chemical reaction[J].,2007,16:421-429.
[9] Vollmer K G,Ettner F,Sattelmayer T. Deflagration-to-detonation transition in hydrogen/air mixtures with a concentration gradient[J].,2012,184(10/11):1903-1915.
[10] Wang C J,Wen J X. Numerical simulation of flame acceleration and deflagration-to-detonation transition in hydrogen-air mixtures with concentration gradients[J].,2017,42(11):7657-7663.
[11] Kessler D A,Gamezo V N,Oran E S. Gas-phase detonation propagation in mixture composition gradients[J].,2012,370(1960):567-596.
[12] Ettner F,Vollmer K G,Sattelmayer T. Numerical investigation of DDT in inhomogeneous hydrogen-air mixtures[C]// 8. Yokohama,Japan,2010.
[13] Ettner F,Vollmer K G,Sattelmayer T. Mach reflection in detonations propagating through a gas with a concentration gradient[J].,2013,23:201-206.
[14] Jiang C,Pan J F,Weng J J,et al. Role of concentra-tion gradient in the re-initiation of H2/O2detonation in a 90° bifurcated channel[J].,2022,120:107281.
[15] Jiang C,Pan J F,Zhu Y J,et al. Influence of concentration gradient on detonation re-initiation in a bifurcated channel[J].,2022,307:121895.
[16] Crank J,Nicolson P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type[J].,1996,6:207-226.
[17] Kurganov A,Noelle S,Petrova G. Semidiscrete central-upwind schemes for hyperbolic conservation laws and Hamilton-Jacobi equations[J].,2001,23(3):707-740.
[18] The OpenFOAM Foundation. OpenFOAM v7[EB/OL]. http://www.openfoam.org/release/7,2019-07-08.
[19] Li J X,Pan J F,Jiang C,et al. Numerical investigation on cellular detonation reflection over wedges with rounded corner[J].,2021,181:503-515.
[20] Zhu Y J,Jiang C,Zhang P G,et al. On the interaction between a diffraction shock wave and a cylindrical sulfur hexafluoride bubble[J].,2021,11(4):045319.
[21] Han W H,Wang C,Law C K. Role of transversal concentration gradient in detonation propagation[J].,2019,865:602-649.
[22] 张 博,白春华. 气相爆轰动力学[M]. 北京:科学出版社,2012.
Zhang Bo,Bai Chunhua.[M]. Beijing:Science Press,2012(in Chinese).
Effect of Concentration Gradient on Detonation Wave Propagation Characteristics in T-tube
Jiang Chao,Pan Jianfeng,Li Jianxing,Ni Jing
(School of Energy and Power Engineering,Jiangsu University,Zhenjiang 212013,China)
To study the effect of concentration gradient on detonation wave diffraction,detonation quenching and re-initiation in a T-tube,the flow field characteristics under two mixtures with three concentration gradients were analyzed based on the open source software OpenFOAM. Results show that the strength of the transverse detonation decreases and detonation is more likely to quench with the increase in the concentration gradient. The interaction between the leading shock and the concentration gradient makes the detonation front bend and changes the propagation process of transverse detonation wave and the Mach stem. For a stable mixture(H2/O2/Ar),the detonation cannot reinitiate,while the detonation successfully reinitiate for an unstable mixture(C2H4/O2).
concentration gradient;detonation wave;cell structure;OpenFOAM
TK16
A
1006-8740(2022)02-0177-06
10.11715/rskxjs.R202202020
2021-03-04.
国家自然科学基金资助项目(51976082,91641113,KYCX20_3022).
姜 超(1992— ),男,博士研究生,jsczjc66@163.com.
潘剑锋,男,博士,教授,mike@ujs.edu.cn.
(责任编辑:武立有)
