基于深度学习的乙烯层流扩散火焰温度和碳烟体积分数分布重建

李智聪，娄 春

基于深度学习的乙烯层流扩散火焰温度和碳烟体积分数分布重建

李智聪，娄 春

(华中科技大学能源与动力工程学院煤燃烧国家重点实验室，武汉 430074)

利用高光谱仪对乙烯层流扩散火焰进行测量，选用多层感知器神经网络预测温度和碳烟体积分数分布，评估了模型的预测和抗噪能力，讨论了不同高度和燃料流量的火焰中温度和碳烟体积分数的分布情况．结果表明，神经网络能较为准确地重建实验火焰的温度和碳烟体积分数，并具有较强的抗噪能力；随着火焰高度的增加，碳烟体积分数峰值从两翼移向中心区域，温度趋于平缓，整体平均大小先增加后减小；随着燃料流量的降低，相同归一化高度的温度升高而碳烟体积分数降低．

乙烯层流扩散火焰；高光谱成像；深度学习；多层感知器；温度；碳烟体积分数

碳烟通常由火焰中燃料的不完全燃烧产生，在实际的燃烧过程中起着重要的作用，对燃烧效率、火焰热辐射和人体健康具有重大影响．为了实现火焰中碳烟颗粒排放的控制，测量火焰中温度和碳烟浓度分布是有必要的[1]．由于非接触式光学测量方法具有较高的时空分辨率，并且不破坏火焰流场，因而得到了广泛使用[2]．常见的火焰光学测量方法可分为基于激光技术和基于火焰自发射光谱的测量，其中火焰自发射光谱测量是利用火焰中固体颗粒(碳烟等)、气相组分(水蒸气、CO2等)以及自由基(OH*等)的发射光谱，使用光谱仪、相机以及高光谱成像仪等设备进行测量．

由于辐射沿视线传递过程中的积累效应，导致火焰温度与介质光谱辐射特性之间具有较强的耦合关系，基于火焰自发射光谱测量火焰内部特性场时通常需要进行反演重建．常用于轴对称火焰的重建算法包括Abel变换[3]和Tikhonov正则化[4]，此外基于启发式随机优化搜索的演化学习算法(粒子群优化算法PSO等)也被用于解决辐射反问题[5]．近年来随着计算机软硬件性能的提升，深度学习在诸多领域得到了广泛应用．深度学习算法能够无需事先确定输入输出之间映射关系的数学方程，仅通过自身的训练学习规则，在给定输入值时得到最接近期望输出值的结果．基于此特性，Huang等[6]将卷积神经网络(convo-lutional neural networks，CNN)用于重建非线性层析吸收光谱，结果表明CNN能够快速精确重建温度分布；Jin等[7]提出了一种基于CNN的3D快速火焰化学发光层析成像重建系统，实际测量结果证明，该CNN模型能够以可靠的精度和结构相似性从实时捕获的投影中重建3D火焰结构；Ren等[8]利用多层感知器(multi-layer perceptron，MLP)神经网络，将Hencken燃烧器气体红外光谱辐射作为测量数据，反演温度分布和气相物质浓度．作为一种常见的实验室轴对称火焰，层流扩散火焰的温度和碳烟浓度分布已经被多种测量手段进行了实验研究[5,9-10]，但基于深度学习重建扩散火焰中温度和碳烟浓度的研究是相对缺乏的．

本文选取乙烯层流扩散火焰为研究对象，利用高光谱成像仪测量火焰图像和热辐射数据，选用深度学习算法中的多层感知器神经网络作为计算模型，从实验测量数据中预测温度和碳烟浓度分布．并对神经网络模型的预测能力和抗噪能力进行了评估，讨论了不同高度和不同燃料流量的层流扩散火焰中温度和碳烟浓度的分布情况以及变化规律．

1 火焰热辐射正问题

富含碳烟颗粒的层流扩散火焰被认为是有发射、吸收以及透明边界，无散射和外界入射辐射的轴对称介质[10]．在400～1000nm的波长范围内，仅考虑火焰中碳烟颗粒的发射和吸收作用，忽略CO2、H2O等气相组分的影响．使用神经网络预测结果无需重建源项，所以只需得到穿过火焰轴线的视线方向上积累的辐射强度．火焰截面被均匀划分为个同心圆环，f为火焰半径，r为第个圆环相对于轴线的半径，0和2N分别为视线的起始和终止位置，Δl为视线穿过第个网格的距离，每个圆环的温度和碳烟浓度f认为是均匀的，如图1所示．

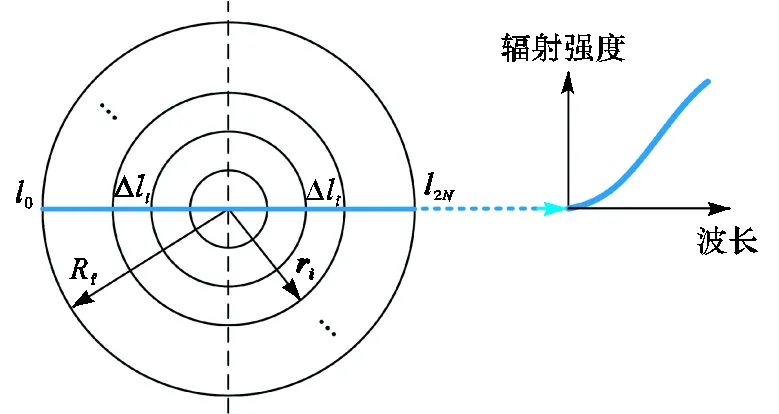
图1 层流扩散火焰水平截面辐射模型

通过正问题计算，得到穿过火焰轴线的视线方向的高光谱辐射强度()：

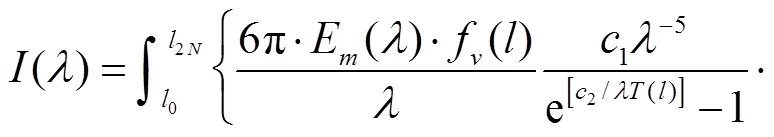
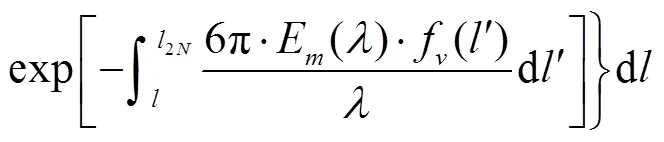
式中：为视线方向上穿过火焰的距离；为波长；为温度；1和2分别为普朗克第一、第二常数；指数项表示火焰辐射沿视线传递过程中的自吸收作用；E为碳烟颗粒复折射率的函数；和分别为复折射率的实部和虚部．复折射率是碳烟颗粒重要的光学特性，对于初生和成熟的碳烟颗粒存在差异．本文需要考虑复折射率在可见光-近红外范围内的变化，采用了Chang等[11]给出的复折射率，因为其广泛应用于火焰碳烟特性的光学测量：

在火焰几何尺寸、火焰中温度和碳烟浓度已知的情况下，通过式(1)～(3)，火焰热辐射正问题计算可为神经网络训练过程提供大量的训练数据．

2 多层感知器神经网络

2.1 计算原理

层流扩散火焰的源项、吸收系数以及自吸收项之间具有较强的耦合关系，使用常规反演算法(Abel变换、Tikhonov正则化等)由式(1)重建火焰中的温度和碳烟浓度分布时需要解决非线性的不适定问题[5].而神经网络能够仅通过自身的训练学习规则，在给定火焰辐射强度时得到最接近真实的温度和碳烟浓度分布．选用的MLP是神经网络的一种，其神经元分层排列，各层间没有反馈．每个神经元与前一层的所有神经元相连，接收前一层的输出，并输出给下一层．如图2所示．

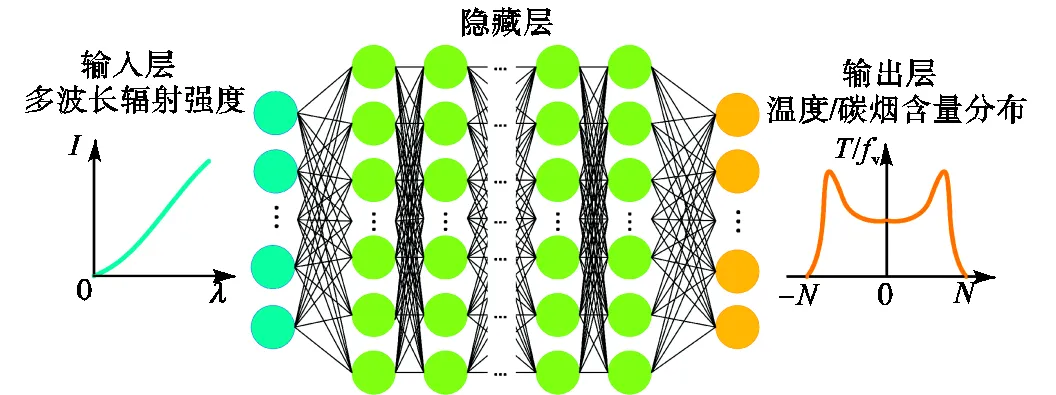
图2 MLP神经网络原理

MLP神经网络中的每个神经元都进行独立的计算，输入值是上一层所有神经元的输出，输出值是通过激活函数转换的输入的加权和：

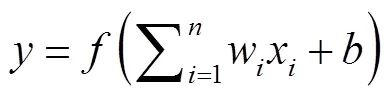
式中：w为上一层神经元与该神经元之间的连接权重；b为该神经元的阈值；f为激活函数，目前常用整流线性单位(rectified linear units，ReLU)，即f(x)＝max{0，x}．神经元的计算原理如图3所示．

2.2 神经网络的构建、训练及优化

基于Python 3.7构建MLP神经网络，使用Keras框架，全部计算在Intel Core i5-8250U上执行．根据实验测量的高光谱辐射强度以及火焰网格划分，构建的MLP神经网络输入层包含256个神经元，输出层包含200个神经元，其中温度和碳烟浓度各为100个．结合实验数据逐步调整，确定隐藏层层数为11层，每层神经元个数为500个．

训练是指使用优化算法更新权重和阈值，使损失函数(loss function)最小的过程．首先将权重和阈值初始化赋值为均值为0、方差为1的正态分布，其中学习率(learning rate)是训练过程中一个较难设置的超参数，选用了具有自适应学习率的Adam算法，该算法已被证明是一种有效且实用的神经网络优化算法[12]．对于回归问题，损失函数常为均方误差(mean squared error，MSE)，即

式中：为神经网络输出结果的标签值(真实值)；′为神经网络的预测值；0为输出层神经元个数；为权衡2正则化项和标准目标函数相对贡献的超参数.

训练使用的数据集分为输入、输出数据两部分，输入数据为高光谱辐射强度，输出数据为温度和碳烟浓度，其中输出数据的选取对神经网络预测能力的影响尤为重要．为了尽可能准确表示实际火焰中温度、碳烟浓度的分布情况，将Liu等[13]使用相干反斯托克斯拉曼散射CARS和激光消光LE技术测得的与本文实验工况相同的乙烯扩散火焰温度、碳烟浓度径向分布作为基准，归一化后生成训练数据集．考虑的温度范围为300～3000K、碳烟浓度范围为0～25×10-6：

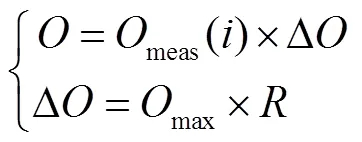
式中：代表训练数据集中的输出数据，即温度/碳烟浓度分布；meas为归一化测量结果；Δ为输出数据变化幅值；max为输出数据范围的最大值，对于温度和碳烟浓度为3000和25；为0～1之间的随机数；为网格数．利用输出数据，可通过正问题计算得到输入数据，即穿过火焰轴线的视线上的高光谱辐射强度．考虑在实验测量过程中可能引入误差，对输入数据添加3%的随机噪声．

在可见光-近红外范围内，不同输出数据计算得到的输入数据的光谱分布趋势较为接近．为了避免该近似性导致MLP神经网络预测能力不足，选取6组对应于火焰高度为10mm、20mm、30mm、40mm、50mm和60mm的归一化测量结果为基准，生成训练数据集分别进行训练．对于每个高度，训练数据集包含1530组数据，其中1500组用于训练神经网络，另外30组作为神经网络“从未见过”的数据对神经网络预测能力进行测试．以上6组基准分布未参与训练．

训练神经网络的目的是使神经网络对于训练数据和测试数据均能预测出准确结果．神经网络对于全新输入数据的良好预测能力被称为泛化能力．为了提高MLP神经网络的泛化能力和预测精度，采用了以下两种优化方法：①对隐藏层的连接权重中添加2正则化，限制模型的学习能力，防止过拟合；②对输入数据进行归一化处理，提升模型的收敛速度和预测精度．

3 实验设备及工况

图4为扩散火焰实验系统，用于研究空气气氛下不同高度和不同燃料流量的扩散火焰温度和碳烟体积分数分布．Gülder燃烧器用于生成同轴层流扩散火焰，该燃烧器由两个同心圆管组成，中心燃料管内径为10.9mm、外径为12.8mm，氧化剂管的内径为88mm，并且填充小玻璃珠和多空泡沫金属保证气流均匀稳定．高光谱成像仪(型号：SOC710VP)用于获得火焰图像和火焰各点的高光谱辐射信息，其测量光谱波长范围为400～1000nm，光谱分辨率为2.34nm，配备一枚焦距为17mm的定焦镜头(型号：Schneider Xenoplan 1.4/17-0903)．相对于分别使用光谱仪和相机等设备，高光谱仪能够更方便地确定穿过火焰轴线的视线位置．考虑视线的不平行性[14]，造成的测量误差最大为1.8%．高光谱仪的像素值范围为0～4095，为了将每个测量波长的像素值与辐射强度联系起来，利用黑体炉(型号：LumaSense M330)对高光谱仪进行了热辐射强度标定．黑体炉的温度范围为300～1700℃，发射率为0.99，不确定度为±1℃.利用黑体炉作为标准辐射源验证标定的准确性，得到标定结果的误差小于1%．

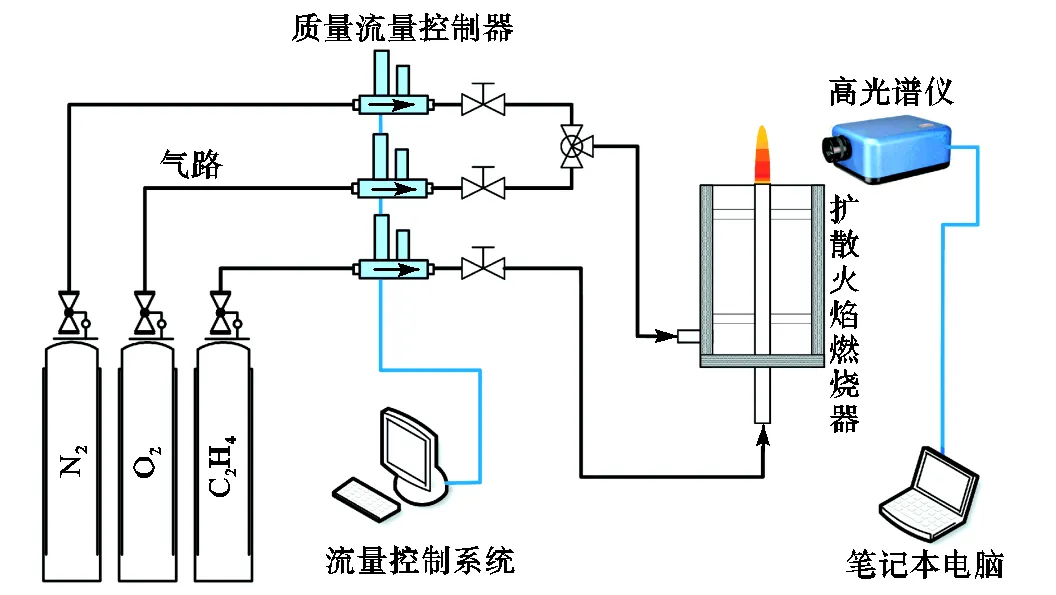
图4 扩散火焰实验系统

为了研究不同高度以及不同燃料流量的层流扩散火焰中温度、碳烟体积分数分布情况，设定了5组工况，燃料均采用乙烯，工况1～5的燃料流量分别为194mL/min、180mL/min、160mL/min、140mL/min和120mL/min；氧化剂总流量均为40L/min，其中氧气体积分数为21%，其余为氮气．所有工况的绝热火焰温度均为2378K．

4 结果分析

4.1 MLP神经网络预测能力

训练过程中训练的次数主要影响损失函数和训练时间，前者代表神经网络的预测能力，后者代表训练神经网络的花费．损失函数随着训练次数的增加逐渐下降，当训练次数大于400之后，损失函数下降缓慢，而训练时间随训练次数线性增长，如图5(a)所示．综合考虑损失函数和训练时间，最终选择的训练次数为400次．训练过程中损失函数的变化情况如图5(b)所示．

图5 训练次数对神经网络训练的影响

训练完成的MLP神经网络能够预测给定辐射强度对应的温度和碳烟体积分数分布．以高度为30mm的基准分布为例，在训练数据中选取分布较为分散的5组输入数据，将其预测结果与标签值进行对比，如图6所示．预测的温度和碳烟体积分数与标签值的平均相对误差分别为6.80%和8.02%，其中工况5的预测结果与标签值存在明显差异．因为温度及碳烟体积分数较小的工况经正问题计算得到的输入数据偏小，归一化之后数据量级更小，导致预测结果存在一定偏差，该问题主要出现在预测温度低于800K的工况时．在可见光-近红外范围内重建火焰温度和碳烟体积分数时，通常考虑800K以上的温度范围，所以MLP神经网络在低温范围内的预测能力不足，不会对实验火焰结果的预测造成显著影响．除去工况5的影响，其余4组工况的平均相对误差分别为1.08%和1.13%．说明训练过程是收敛的，神经网络能够较为准确地预测训练数据的结果．

图6 训练数据预测结果与标签值对比

图7为从测试数据中选取较为分散的4组输入数据(温度大于800K)，神经网络预测结果与标签值的对比．图中预测的温度和碳烟体积分数与标签值的平均相对误差分别为1.40%和1.60%．对于MLP神经网络“从未见过”的数据，较低的相对误差说明神经网络具有良好的泛化能力和预测能力．

为了评估MLP神经网络对于具有较大噪声的实验测量数据的预测能力，对测试数据的输入数据添加不同程度的随机噪声(温度大于800K)，预测结果相对于标签值的误差如表1所示．当随机噪声小于3%时，温度和碳烟体积分数的相对误差均小于图7中测试数据预测结果的误差范围，因为训练数据集添加的噪声就是3%．当噪声大于3%时，预测结果的相对误差逐渐增大；当噪声达到30%时，温度和碳烟体积分数预测结果相对误差分别达到3.36%和3.90%，但仍在较小的范围内，表明MLP神经网络具有较强的抗噪能力．

综合考虑测量误差、标定误差以及测试数据预测结果的相对误差，MLP神经网络预测实验火焰温度和碳烟体积分数的相对误差分别为2.49%和2.61%．

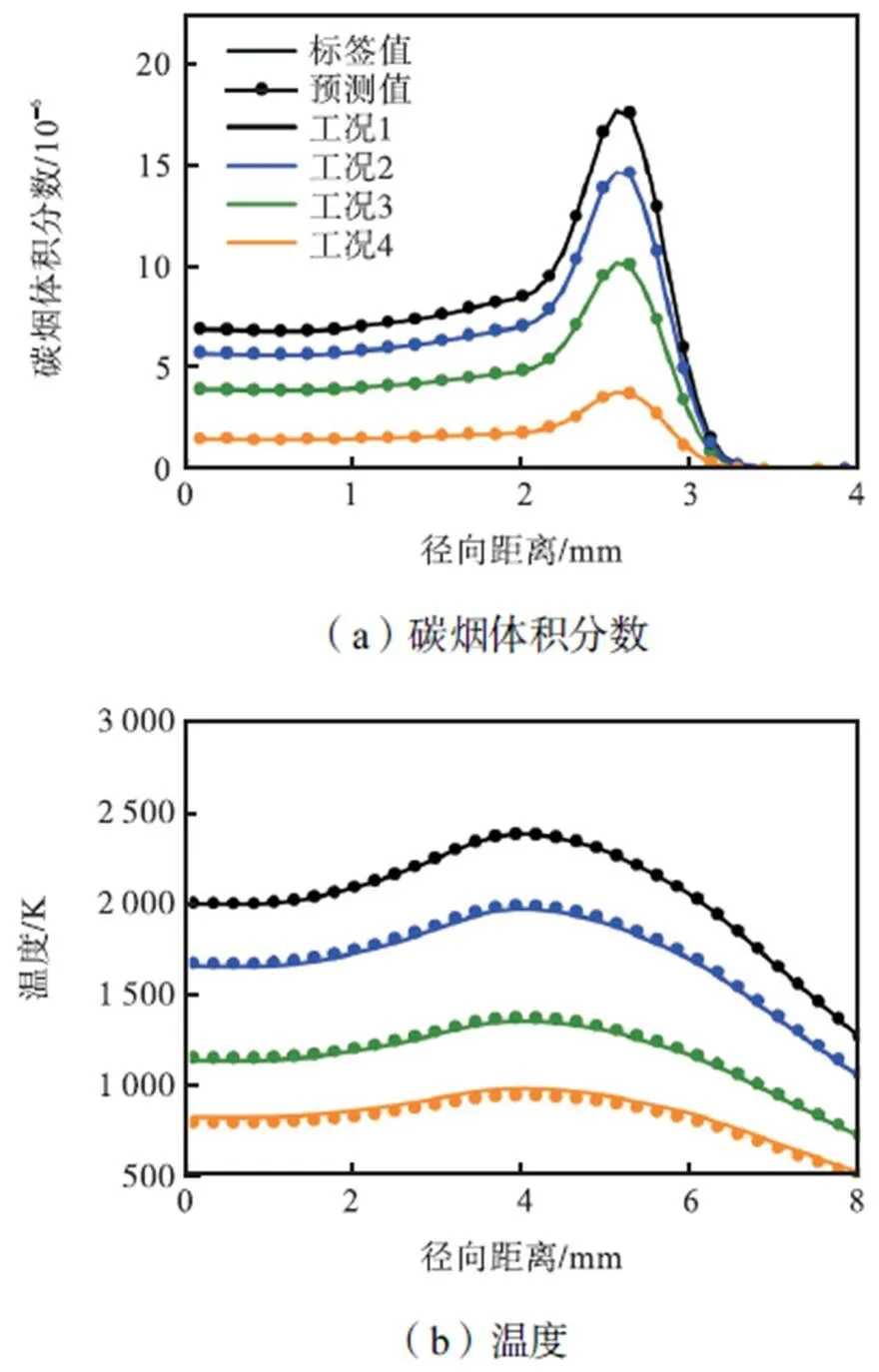
图7 测试数据预测结果与标签值对比

表1 不同噪声输入数据的预测误差

Tab.1 Prediction error of input data with different noises

4.2 实验结果及讨论

随着燃料流量的减少，火焰高度显着降低，工况1～5的高度分别为68mm、60mm、51.5mm、43.5mm和25mm．在相同的曝光时间(2ms)下，火焰的发光强度基本不变，并且所有火焰呈现出明亮的橙黄色．火焰图像以及工况1的高光谱辐射强度分布如图8所示．

4.2.1 不同高度温度和碳烟体积分数分布

乙烯流量为194mL/min并且在Gülder燃烧器上生成的扩散火焰(工况1)，是一个被广泛研究的扩散火焰工况，许多测量技术对其温度和碳烟体积分数分布进行了研究[5,9-10]．将MLP神经网络预测的温度和碳烟体积分数分布与CARS和LE的测量结果[13]、使用Abel反演的多波长发射测量结果[9]以及使用Tikhonov正则化的火焰图像处理测量结果[10]进行比较，验证MLP神经网络预测结果的准确性．以高度为30mm和50mm的结果为例，如图9所示．工况1与其余测量方法的实验工况基本一致，不同之处在于工况1的氧化剂流量为40mL/min，而其余方法使用的为284mL/min．氧化剂过量时，氧化剂流量对扩散火焰的影响很微弱[14-15]，所以工况1可以与其余测量方法的结果进行比较．相对于使用Abel反演的多波长发射测量以及使用Tikhonov正则化的火焰图像处理，MLP神经网络的预测结果更加接近激光测量技术的结果，尤其是对于碳烟体积分数的预测．尽管预测结果并不完全一致，但分布趋势基本相同且误差很小，表明MLP神经网络能够准确地预测实验火焰的温度和碳烟体积分数分布．

图8 实验火焰及高光谱辐射强度

图10为利用MLP神经网络预测的工况1对应于6组基准分布的火焰高度的温度和碳烟体积分数分布．随着火焰高度增加，火焰宽度变窄，碳烟体积分数峰值位置从火焰两翼移向火焰下游中心区域，温度分布趋于平缓．温度峰值位置始终位于碳烟体积分数峰值外侧，因为火焰最高温度通常出现在火焰面上，而碳烟在靠近火焰面的燃料侧被氧化，体积分数下降．温度和碳烟体积分数的整体水平先增加后减小，因为在燃烧器喷嘴附近(10mm)，燃料发生热解并向氧化剂侧移动，火焰中心区域温度明显低于两翼，且该高度的碳烟成核和表面成长速率较慢，碳烟体积分数较低；在火焰中部(20～40mm)，火焰中充斥着燃料热解产生的大量自由基以及形态多样的碳烟颗粒，各种反应剧烈进行，导致温度和碳烟体积分数升高；在火焰下游(50～60mm)，碳烟颗粒被氧化，并且由于火焰宽度变窄以及氧化剂的扩散作用，碳烟体积分数峰值出现在火焰轴线处，温度由于可燃物质浓度的降低而降低．

图9 不同测量方法的温度和碳烟体积分数结果对比

图11为火焰中心轴线上不同高度的温度和碳烟体积分数．碳烟体积分数先增加后减少，因为随着高度增加，碳烟颗粒的初生成核、团聚和表面成长、氧化依次占据主导地位；温度上升至碳烟体积分数最大值高度附近(30～40mm)处略微下降，随后继续上升，可能是在碳烟团聚和表面成长过程中吸热反应影响较大，而在氧化过程中释放大量热量导致的．

4.2.2 不同乙烯流量温度和碳烟体积分数分布

讨论工况1～5的温度和碳烟体积分数分布时，为避免火焰高度的影响，选用归一化高度为0.441和0.735的实验测量数据进行预测(工况1的30mm、50mm对应的归一化高度)，预测结果如图12所示．在归一化高度为0.441处，5组火焰的宽度基本一致，忽略火焰宽度的影响；而在归一化高度为0.735处，火焰宽度随乙烯流量的下降明显变窄，基于实验图像的火焰宽度对图12(b)中的分布进行调整．

随着乙烯流量的降低，两组归一化高度的温度和碳烟体积分数表现出相同的变化规律，即温度升高而碳烟体积分数降低. 因为燃料流量的减少会降低火焰反应区中的燃料浓度，且燃料热解产生的C2H2会减少，燃料和C2H2的相对缺乏在一定程度上放缓了碳烟的生成；而较小的燃料流量、较低的火焰高度和碳烟体积分数降低了火焰与环境之间的辐射热损失，尽管所有工况具有相同的绝热火焰温度(ad＝2378K)，但热量损失的减少会促使火焰温度略微升高.

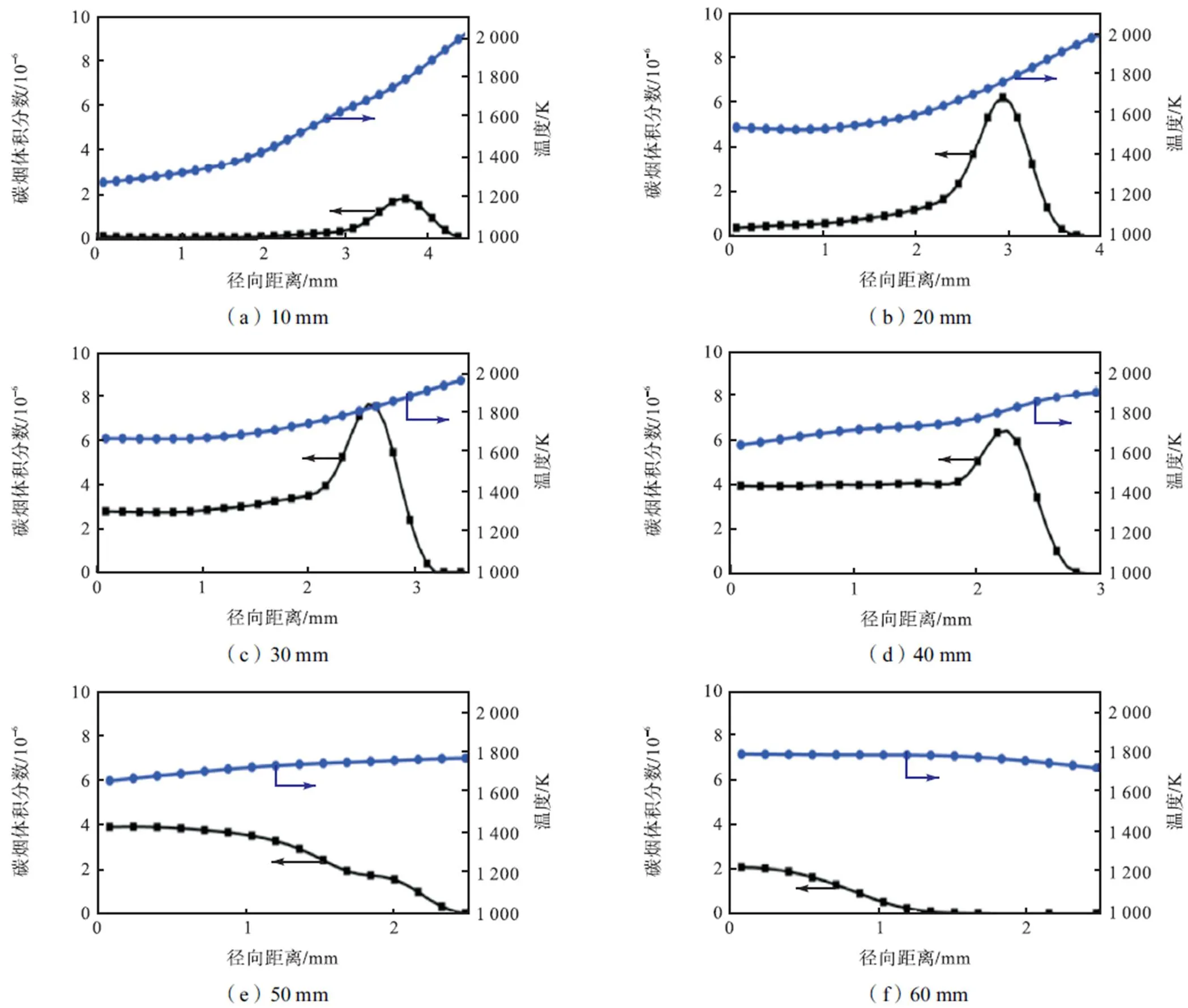
图10 不同高度的温度和碳烟体积分数径向分布

图11 火焰轴线的温度和碳烟体积分数分布

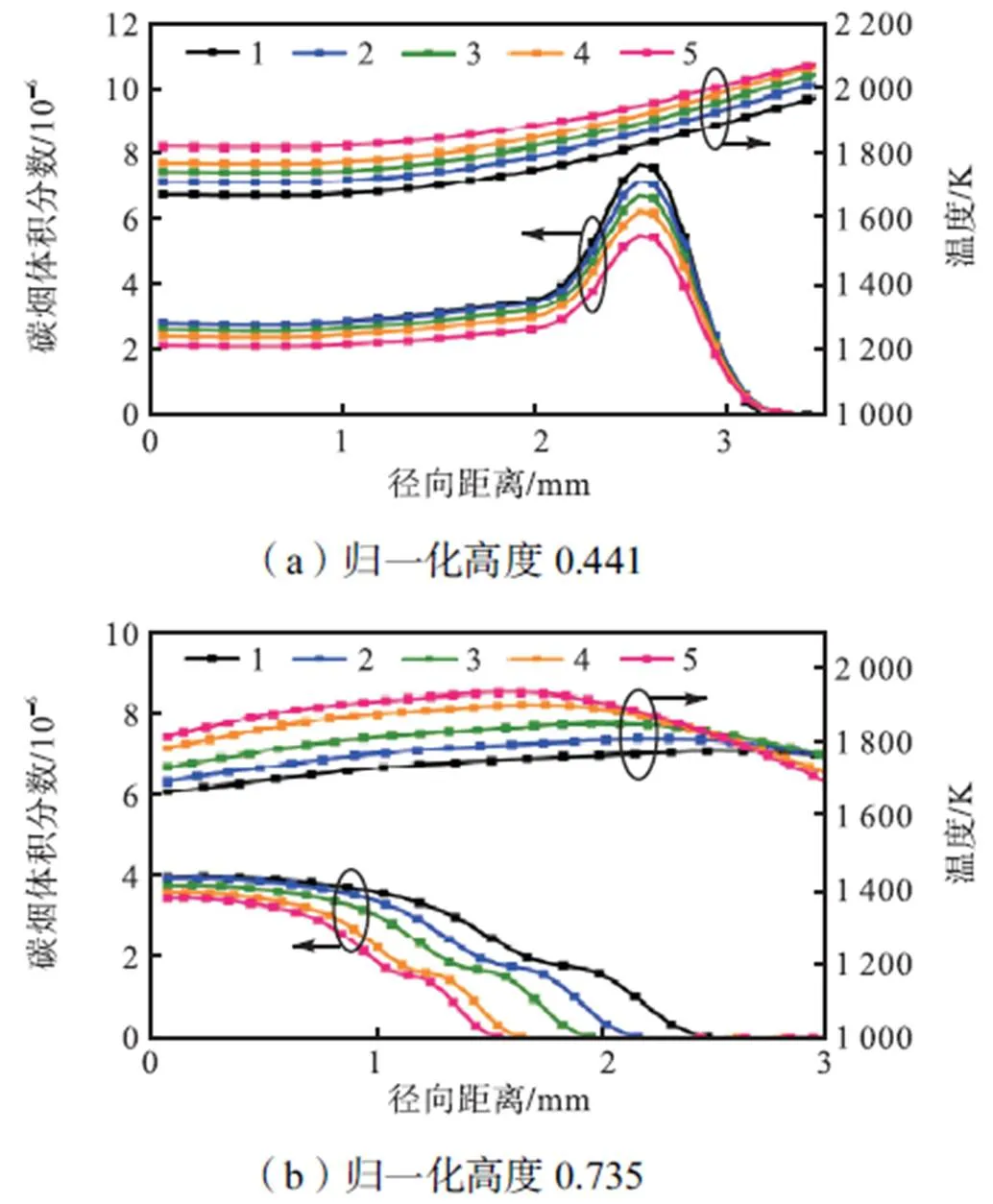
图12 相同归一化高度的温度和碳烟体积分数分布对比

5 结 论

(1) 训练完成的MLP神经网络能够准确地重建实验火焰的温度和碳烟体积分数分布，相对误差分别为1.40%和1.60%．

(2) MLP神经网络具有较强的抗噪能力，当高光谱辐射强度的噪声达到30%时，温度和碳烟体积分数预测结果相对误差分别为3.36%和3.90%．

(3) 随着火焰高度的增加，火焰宽度逐渐变窄，碳烟体积分数峰值位置从火焰两翼移向中心区域，温度分布趋于平缓．温度和碳烟体积分数的整体平均大小先增加后减小．

(4) 随着火焰高度的增加，火焰中心轴线的碳烟体积分数先增加后减少；温度先升高，在碳烟体积分数最大高度处略微下降，随后继续上升．

(5) 随着乙烯流量的降低，相同归一化高度的温度略微升高而碳烟体积分数降低．

［1］ Lou C，Chen C，Sun Y P，et al. Review of soot measurement in hydrocarbon-air flames[J].：，2010，53(8)：2129-2141.

［2］ 娄 春，张鲁栋，蒲 旸，等. 基于自发辐射分析的被动式燃烧诊断技术研究进展[J]. 实验流体力学，2021，35(1)：1-17.

Lou Chun，Zhang Ludong，Pu Yang，et al. Research advances in passive techniques for combustion diagnostics based on analysis of spontaneous emission radiation[J].，2021，35(1)：1-17(in Chinese).

［3］ Dasch C J. One-dimensional tomography：A comparison of Abel，onion-peeling，and filtered backprojection methods[J].，1992，31(8)：1146-1152.

［4］ Daun K J，Thomson K A，Liu F，et al. Deconvolution of axisymmetric flame properties using Tikhonov regularization[J].，2006，45(19)：4638-4646.

［5］ Sun Y P，Lou C，Zhou H C. Estimating soot volume fraction and temperature in flames using stochastic particle swarm optimization algorithm [J].，2011，54(1/2/3)：217-224.

［6］ Huang J，Liu H，Dai J，et al. Reconstruction for limited-data nonlinear tomographic absorption spectroscopy via deep learning[J].，2018，218：187-193.

［7］ Jin Y，Zhang W，Song Y，et al. Three-dimensional rapid flame chemiluminescence tomography via deep learning[J].，2019，27(19)：27308-27334.

［8］ Ren T，Modest M F，Fateev A，et al. Machine learning applied to retrieval of temperature and concentration distributions from infrared emission measurements[J].，2019，252：113448.

［9］ Snelling D R，Thomson K A，Smallwood G J，et al. Spectrally resolved measurement of flame radiation to determine soot temperature and concentration[J].，2002，40(9)：1789-1795.

［10］ Yan W，Lou C. Two-dimensional distributions of temperature and soot volume fraction inversed from visible flame images[J].，2013，50：229-233.

［11］ Chang H，Charalampopoulos T T. Determination of the wavelength dependence of refractive indices of flame soot[J].：，1990，430：577-591.

［12］ Goodfellow I，Bengio Y，Courville A. 深度学习[M]. 北京：人民邮电出版社，2017.

Goodfellow I，Bengio Y，Courville A.[M]. Beijing：Posts & Telecom Press，2017(in Chinese).

［13］ Liu F，Guo H，Smallwood G J，et al. Effects of gas and soot radiation on soot formation in a coflow laminar ethylene diffusion flame[J].，2002，73(2/3/4/5)：409-421.

［14］ Li Z，Zhang L，Lou C.measurement of soot volume fraction and temperature in axisymmetric soot-laden flames using TR-GSVD algorithm[J].，2021，70：5001212.

［15］ Lou C，Li Z，Zhang Y，et al. Soot formation characteristics in laminar coflow flames with application to oxy-combustion[J].，2021，227：371-383.

Reconstruction of Temperature and Soot Volume Fraction Distribution of Ethylene Laminar Diffusion Flame Based on Deep Learning

Li Zhicong，Lou Chun

(State Key Laboratory of Coal Combustion，School of Energy and Power Engineering，Huazhong University of Science and Technology，Wuhan 430074，China)

A hyperspectral imager was used to measure the ethylene laminar diffusion flame，the multi-layer perceptron(MLP) neural network was used to predict the distributions of temperature and soot volume fraction，the prediction and anti-noise ability of the MLP model were evaluated，and the distributions of temperature and soot volume fraction in flames of different heights and fuel flow rates were discussed. The results show that the neural network can more accurately reconstruct the temperature and soot volume fraction of the experimental flame and has a strong anti-noise ability. As the flame height increases，the peak soot volume fraction moves from the wings to the central region of the flame，the temperature tends to be flat，and the overall average size first increases and then decreases. As the fuel flow rate decreases，the temperature at the same normalized height increases while the soot volume fraction decreases.

ethylene laminar diffusion flame；hyperspectral imaging；deep learning；multi-layer perceptron；temperature；soot volume fraction

TK16

A

1006-8740(2022)02-0198-08

10.11715/rskxjs.R202202013

2021-02-18．

国家自然科学基金资助项目(51827808；51676078).

李智聪（1997—  ），男，博士研究生，lzc97@hust.edu.cn，1002953665@qq.com.

娄 春，男，博士，教授，lou_chun@sina.com.

(责任编辑：隋韶颖)