一类复合随机变量概率分布的说明

徐 怀

(安徽大学 数学科学学院，安徽 合肥 230039)

0 引言

复合随机变量在各个领域有着广泛的应用，在各种风险模型中，一般以复合随机变量来刻画索赔过程或收入过程[1-6].在排队模型中，复合随机变量用来描述等待时间和服务时间[7-9].复合随机变量概率分布自然也就成为一个中心议题.本文将以卷积公式为基础，在连续型随机变量情形下，给出概率密度函数的积分公式，在离散型的情形下给出概率分布列的迭代公式，这个迭代公式为实际应用奠定了坚实基础.考虑到实际应用的问题，最后本文给出一个把连续型随机变量离散化得出复合随机变量近似分布函数的数值例子.

下面首先给出相关定义.

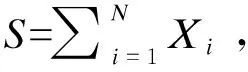
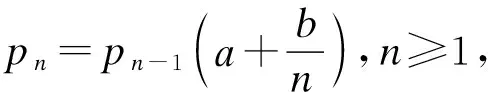
可以证明除退化分布外，此类分布包含且仅包含泊松分布、二项分布、负二项分布，这些分布在精算领域内有着广泛的应用[10-11].

为完成主要结论的说明，先声明如下简单事实：

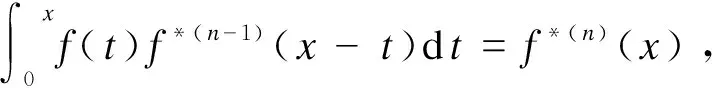
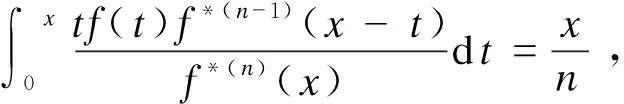
类似地，当{Xi，i≥1}是非负整数离散型随机变量，其概率分布列记为fi=P(X1=i)，则有类似2个结论：

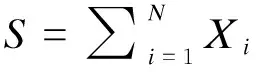
1 离散型情形下概率分布列的迭代公式

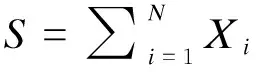
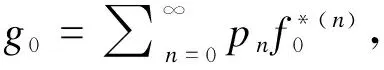
证明：

下证gi，i≥1.

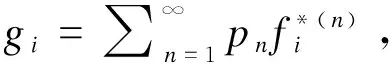
所以

(1)

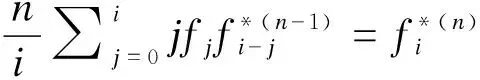
(2)

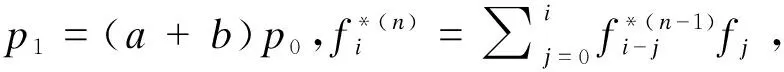
(3)

分解式(3)中的第二和第三项得

(4)

分解式(4)的第一项，分别与第三项和第五项合并得

(5)

分别合并式(5)的第一和第三项，第二和第四项得

(6)

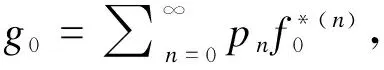
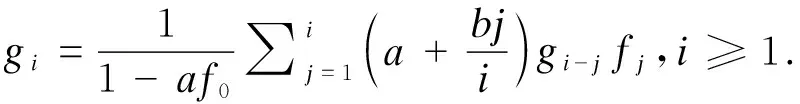
2 连续型情形下概率密度函数的积分公式

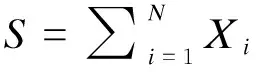
证明：

首先对概率密度函数应用全概率公式得

(7)

交换积分和求和的顺序，得

整理得

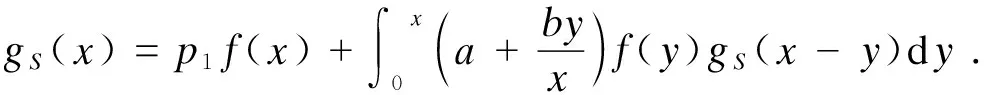
3 数值例子

本文需要指出的是，在实际应用中，定理1的应用比定理2的应用更为广泛，因为通过定理2给出解析解是比较困难的，而定理1却没有这样的困难，所以若Xi是非负连续随机变量，本文考虑将其离散化[12-14]，然后给出复合随机变量的分布函数的近似表达式.在这一节中将详细讨论.

设非负连续型随机变量Xi的密度函数为f(x)，首先考虑2个随机变量Xd，Xu，其取值为

这样有FXu(x)≥FXi(x).

P(Xd=0)=0，

这样有FXl(x)≤FXi(x).

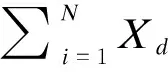
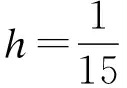
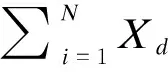
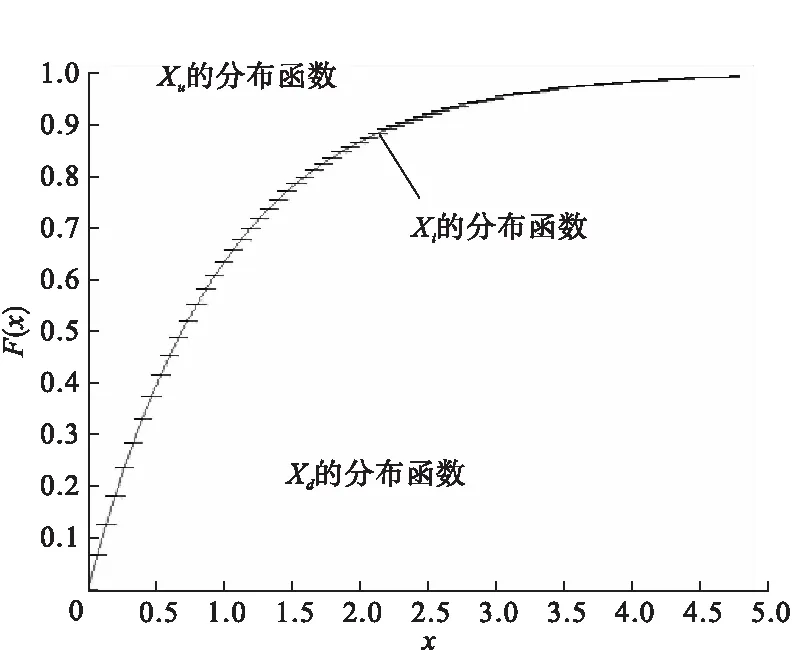
图1 Xd，Xu，Xi的分布函数

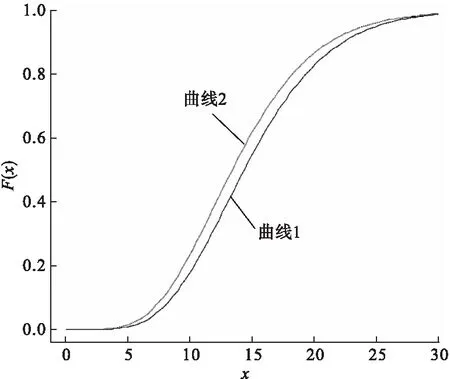
图和的分布函数

4 小结

复合随机变量有着广泛的应用，文中考虑了当计数过程是(a，b，0)分布类且Xi为非负随机变量时复合随机变量概率函数的迭代公式、积分公式，以及近似计算方法等问题，最后结合数值例子加以阐释.本文希望这样的讨论能对解决类似问题提供有益的思路.