六翼混沌系统及其同步控制

颜闽秀，张 萍

(1.沈阳化工大学 信息工程学院，辽宁 沈阳 110142； 2.工业环境-资源协同控制与优化技术辽宁省高校重点实验室，辽宁 沈阳 110142)

0 引言

混沌系统是非线性动力学系统，具有对初值高度敏感性、类随机性、不确定性和非周期性等特征，广泛应用于保密通信、信息加密等领域.自从1963年，美国气象学家Lorenz发现Lorenz混沌系统[1]后，混沌控制逐渐成为热点.之后，Chen系统[2]、Liu系统[3]等不同类型的混沌系统陆续被提出.近几年来，为增强混沌系统在保密通信中的安全性能，学者们陆续探索具有更为复杂吸引子的混沌系统.因此切换混沌系统[4]构造成为一个研究热点.

文献[5]利用一次坐标变换提出四翼混沌系统，通过切换函数来进行混沌系统切换.文献[6]利用开关控制作为切换方法.文献[7]基于Lorenz系统，通过修改非线性项形成子系统.文献[8]对Lorenz系统第2个方程中的y变为-y得到新系统.而本文通过多次坐标变换的方法，得到2个子系统，在切换方法上，设计新的切换系统，提出六翼混沌系统，其混沌系统更具复杂性.同时，在应用方面，同步控制极为重要.文献[9]利用自适应控制器的设计，使驱动系统和响应系统达到同步.文献[10]探讨了自适应滑模控制方法，该同步控制优点在于误差收敛速度更快.本文在参数未知情况下，推导出一种自适应控制律，实现了未知参数的混沌系统的同步，并使其同步时间更短.

本文在Lorenz混沌系统的基础上，通过坐标变换得到混沌子系统，接下来利用切换函数构造新的六翼混沌系统，实现子系统切换.仿真结果表明，该混沌切换系统具有比原系统更为复杂的非线性动力学行为，由于混沌系统相对复杂，因此能够广泛应用于同步通信及加密等领域.

1 Lorenz对称混沌系统

1.1 对称混沌系统

本文考虑Lorenz混沌系统为

(1)

其中，a，b，c为常数参数，其参数值为a=10，b=28，c=8/3.由于该系统存在对称性，对该混沌系统进行(x1，x2，x3)→(x1，x2，-x3)变换，本文即可得到关于x3=d平面对称的新系统(2)，其中d为未知参数.

(2)

本文对混沌系统(1)进行(x1，x2，x3)→(x1，-x2，-x3)变换，即可得到关于x2=e新系统(3)，其中e为未知参数.

(3)

对于系统(2)和系统(3)均有

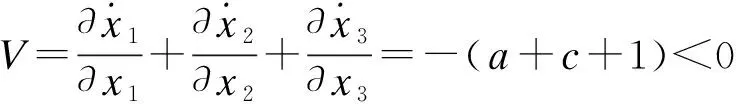
(4)

所以系统是耗散的，并以指数形式收敛.当t→∞时，所有系统的轨线最终会被限制在一个体积为0的点集合上，并且它的渐近行为会被固定在一个吸引子上.

1.2 系统的吸引子

本文令(1，1，1)为系统(1)的初始值，(1，1，-1)为系统(2)的初始值，(1，-1，-1)为系统(3)的初始值，在MATLAB中绘制3系统吸引子图像，如图1所示.

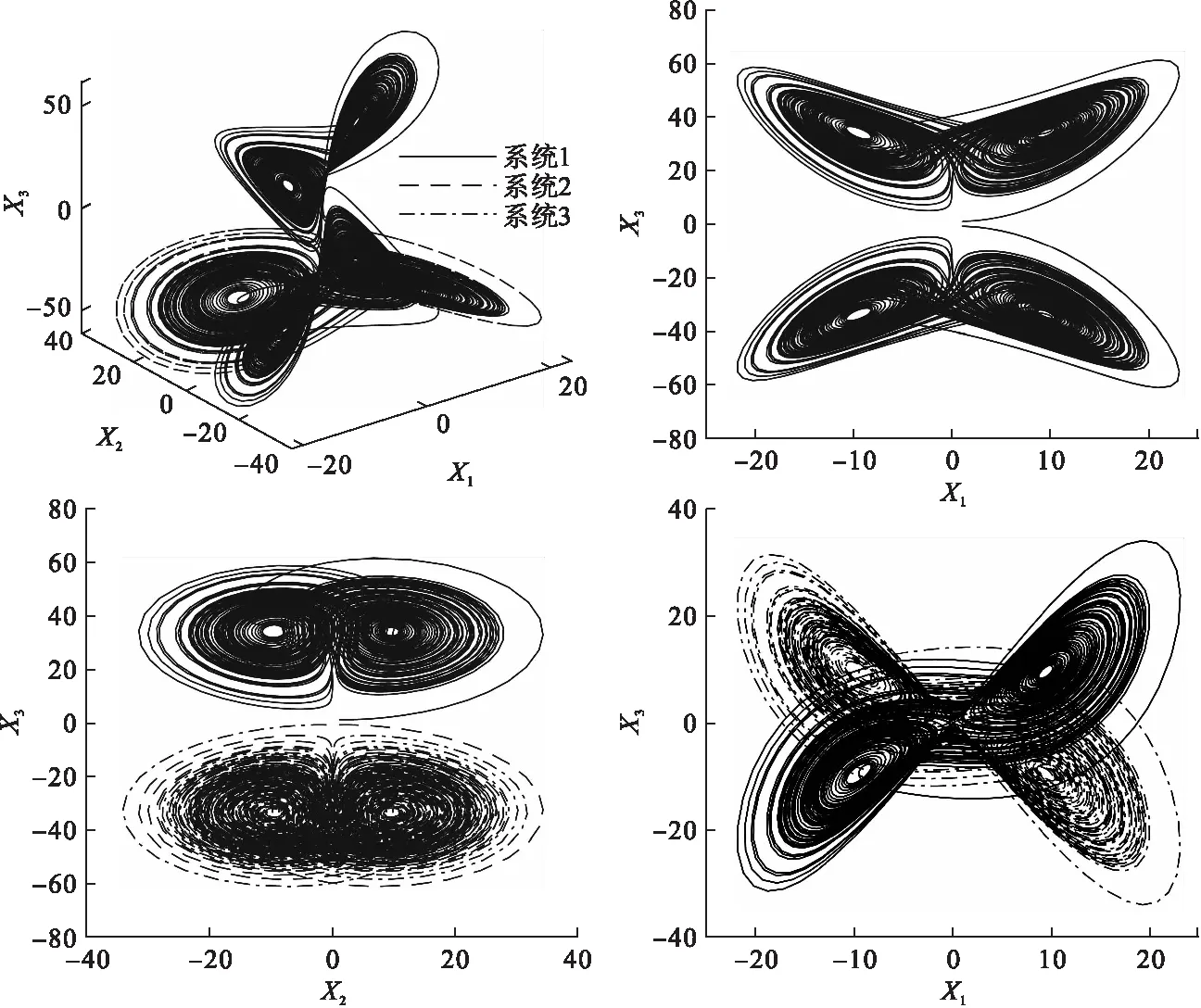
图1 系统(1)、(2)、(3)吸引子及其相图

由图1可知，对称系统为混沌系统.并由图1分析可得，系统(1)和系统(2)吸引子关于X3=0对称，由此可得d为0；系统(1)和系统(3)吸引子关于X2=0对称，由此可得e为0.

接下来，本文设计切换混沌模型函数，实现子系统进行转换，从而使得系统(1)、系统(2)和系统(3)可以构成多翼的对称切换混沌系统.

2 六翼对称切换混沌系统

本文设计的对称切换混沌系统模型

(5)

其中f1、f2为切换函数，用于实现系统(1)、(2)与(3)的切换，其表达式如下：

(6)

ω≠0为一常数，这里取ω=0.02，绘制切换函数图，如图2所示.

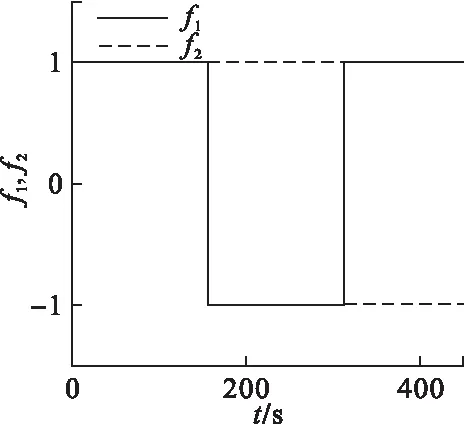
图2 切换函数图

由图2分析可得，一个周期的时间为T，在第1个T/2内f1=1，f2=1，系统(5)先以系统(1)模型运行，在第2个T/2内f1=-1，f2=1，系统(5)以模型(3)运行，在第3个T/2内f1=1，f2=-1，系统(5)以模型(2)运行，之后，反复在模型(3)与模型(2)中运行切换.

本文令(1，1，1)为模型(5)的初始值，绘制吸引子图像，x1-x3相图、x2-x3相图和庞加莱截面图，如图3所示.

由图3吸引子图像可以看出，系统(5)的吸引子是由系统(1)、系统(2)和系统(3)模型的吸引子构成.同时，可以看出，系统在不同截面的庞加莱截面图是由密集点构成的非封闭曲线，由此可以判断，系统(5)是混沌的.由图3相图可以看出系统(5)的运行状态为系统(1)→(3)→(2).

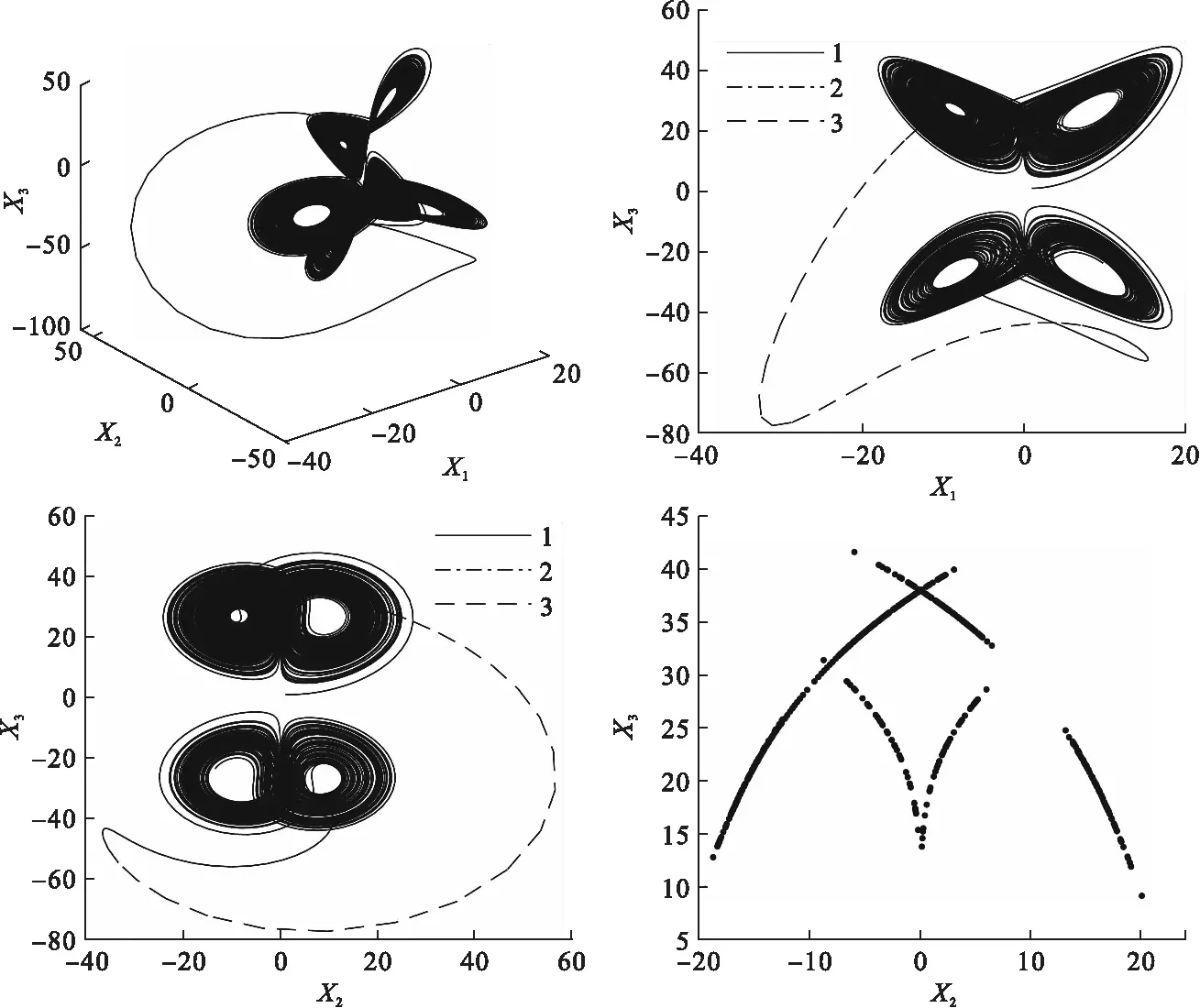
图3 系统(5)的吸引子图、相图及庞加莱截面图

为进一步验证该系统的混沌特性，本文绘制系统的李雅普诺夫指数图和功率谱，分别如图4和图5所示.

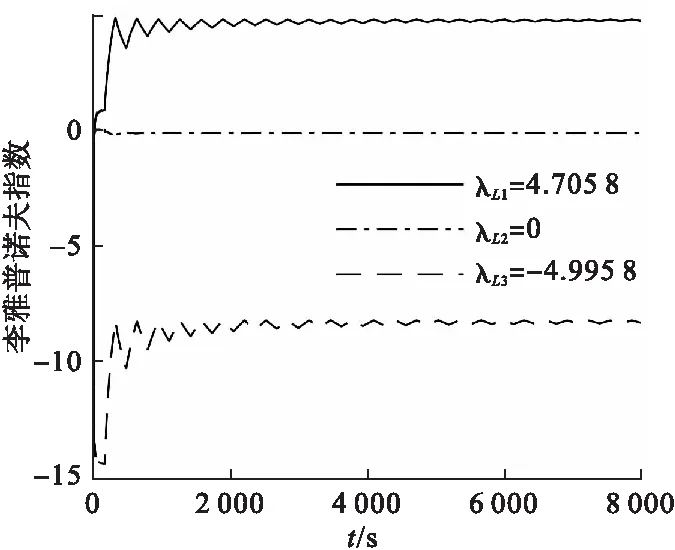
图4 李雅普诺夫指数图

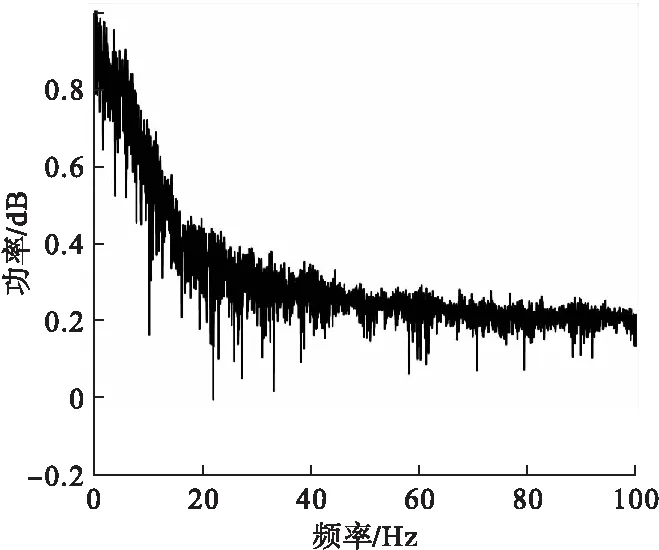
图5 功率谱

同时，由图4可知，计算出李雅普诺夫维数DL为

DL=2+(λL1+λL2)/λL3=2.941 9

(7)

因λL1为正数，DL为分数，同时，又有功率谱为连续谱，没有明显的波峰，由此进一步验证了系统(5)的混沌特性.

3 基于李雅普诺夫理论和自适应控制理论同步控制

3.1 理论分析

本文令式(5)作为驱动系统，对应的响应系统为

(8)

同步误差定义为

(9)

因此，同步误差系统为

(10)

考虑设计自适应控制律为

(11)

其中，k1，k2，k3为正增益常数.

由式(11)代入式(10)可得，闭环误差动态方程为

(12)

设置参数估计误差为

(13)

因此，方程(12)可以转换成

(14)

对式(13)进行微分可得

(15)

取李雅普诺夫函数为

(16)

对其求导可得

(17)

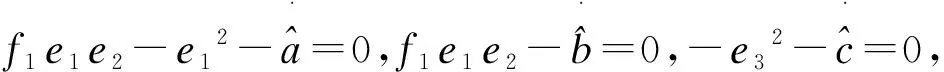
(18)

所以，可以得到

(19)

由李雅普诺夫稳定性理论可知，误差系统是渐近稳定的，驱动系统与响应系统能够同步.

3.2 数值仿真

为验证控制器有效性，本文在MATLAB中进行数值仿真实验，取驱动系统的初始值为(-1，2，0.1)，响应系统的初始值为(1，2，-2)，设置控制参数kn=20，n=1，2，3，令未知参数a=5，b=4，c=3.

本文基于上述数据进行仿真实验，同步误差结果如图6所示.

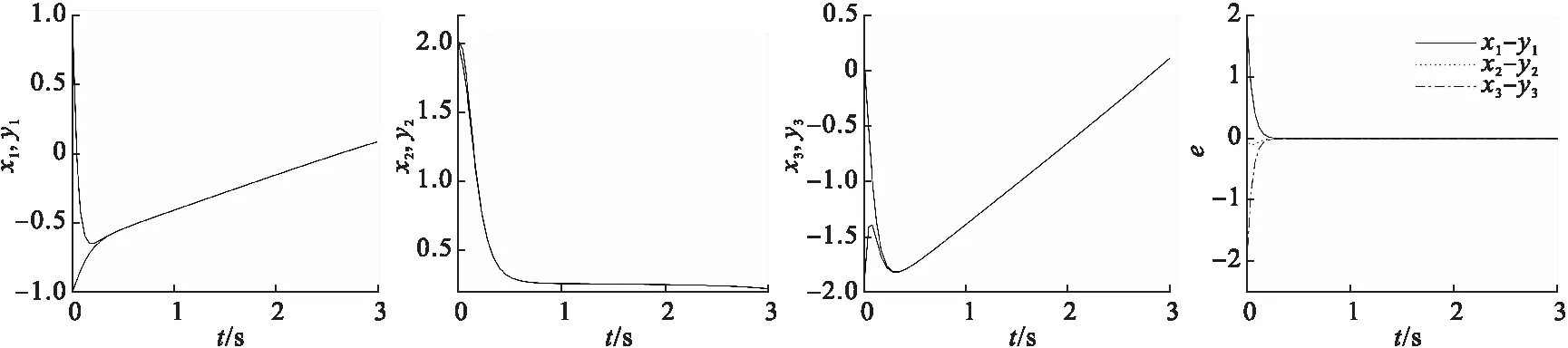
图6 同步误差

由图6可以看出，驱动系统和响应系统能够很快达到同步，同步误差能够在较短时间内趋近于零，从而实现同步.

4 结论

本文提出了1个新的六翼混沌系统，通过吸引子图、相图、庞加莱截面图、李雅普诺夫指数以及功率谱分析说明系统具有复杂的动力学特性，验证系统的混沌特性.同时，本文设计自适应同步控制器，在参数未知情况下实现驱动系统与响应系统的同步控制.该系统比Lorenz系统更具复杂性，因此在同步通信和数字图像加密领域有重要的应用价值.