侧面作用移动热源柱体温度场适体坐标有限容积法数值解与分析解的对比
2022-04-26石广田翟婉明王良璧
王 璐,石广田,翟婉明,3,王良璧
(1. 兰州交通大学 机电工程学院,兰州 730070;2. 铁道车辆热工教育部重点实验室(兰州交通大学),兰州 730070;3. 西南交通大学牵引动力国家重点实验室,成都 610031)
由摩擦生热产生的移动热源会对车轮及钢轨的性能产生较大的影响[1-7].从而,对车轮和钢轨在移动热源的作用下温度场特性的研究非常重要[8-10].由于这类移动热源问题的复杂性无法用解析法获得温度场.又由于铁道车辆轮轨工作的特殊性,一比一的实验方法也非常难于实施,实验室中的实验数据由于很难转化到可应用到实际情况的数据而受到了限制.这样数值方法成为研究车轮在移动热源作用下温度场特性的有效方法.从而非常有必要发展该类问题的数值方法及实施的程序.目前在用的商业软件很多,但大多数软件处理有追赶特点移动热源问题的边界条件时非常复杂[10].另外,关于数值方法的严格考核报道的较少.鉴于这些原因,论文拟发展一适合处理追赶特点移动热源边界的有限容积法数值分析程序.并与分析解进行比对,验证其数值分析程序的正确性.
1 问题的物理数学描述
1.1 有量纲参数描述
图1所示是半径为r0的一无限长柱体,在柱体侧面上作用有一段AB的移动热源,移动速度为v,移动热源的强度为均匀强度qb.作用面积是2φ0对应的弧长和柱体长度的乘积.除移动热源加热外,在柱体表面上有表面传热系数为常数h的对流传热过程.物理问题是用数值方法确定其温度场.
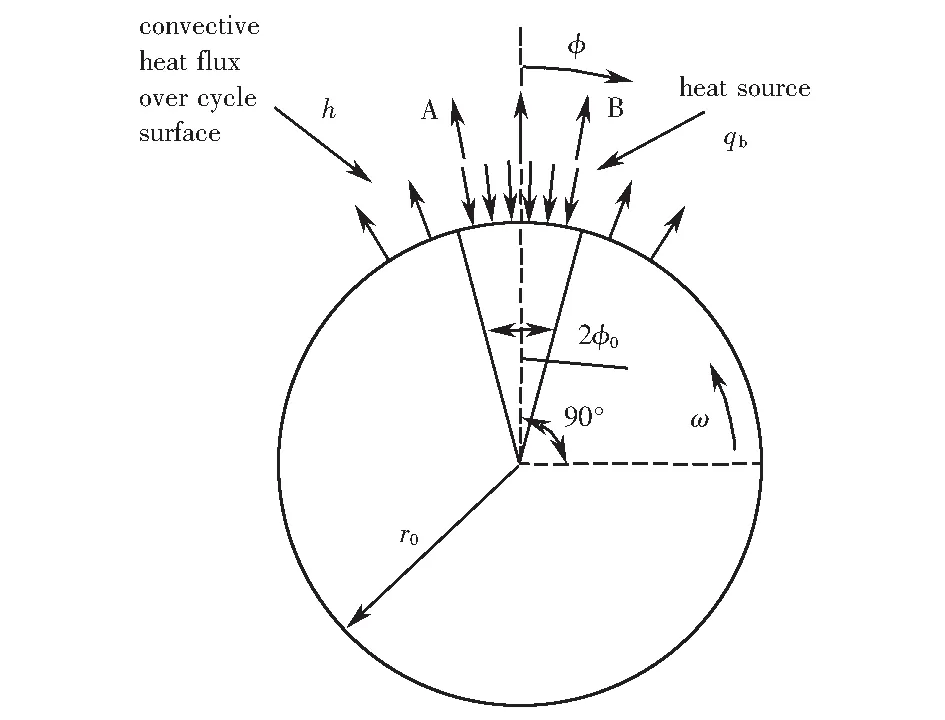
图1 侧面作用移动热源的无限长柱体模型Fig.1 Infinite cylinder model of moving heat source action on the side surface
问题的数学描述为能量守恒定律:
(1)
方程(1)是非稳态热传导微分方程,其中ρ为密度,cp为比热容,T为温度,t为时间,为拉普拉斯算子,λ为导热系数.
方程(1)的边界条件为:
热源作用区2φ0作用的热通量
(2)
侧面对流传热区(包含热源作用区与非作用区)
(3)
这里h是均匀的.
方程(1)的初始条件为:
T0=Tf=0,t≤0.
(4)
1.2 无量纲参数描述
为了无量纲化方程(1),这里无量纲定义如下:
θ=πλvT/(2αqb).
(5)
(6)
X=vx/2α,Y=vy/2α,Z=vz/2α.
(7)
则上述描述变为:
(8)
在热源作用区
(9)
侧面对流传热区(包含热源作用区与非作用区)
(10)
初始条件
θ=θ0,t*≤0.
(11)
θw=πλvTw/(2αqb),θf=0,θ0=0.
(12)
2 数学模型的解析解
对于上述问题文献[14]中给出了解析解:
(13)
这里
(14)
及
(15)
(16)
这里μn,j是下列式子的根.
(17)
这里有:
(18)
J-n(x)=(-1)nJn(x).
(19)
(20)
(21)
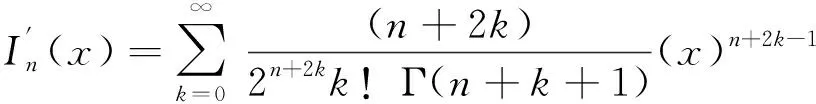
(22)
bernx+ibeinx=inIn(xi1/2).
(23)
(24)
(25)
对于钢件,由于α比较小,大约是10-6的数量级,从而即便是中等角速度,ωn也有较大的数值,根据I(x)的特性,I(ωn)在较小的n条件下就会有I(ωn)→∞.这样会使得式(15)~(16)的计算没有意义(数值为∞).在这种情况下需要把bern(x)及bein(x)表示成另外一种形式,使得M1(x),M2(x),M3(x)成c1·exp(c2x)的形式,然后带入式(14),消去exp(x)后就可保证式(14)的数值有意义(不会是∞).
文献[15]给出了bern(x)及bein(x)这种形式:
(26)
(27)
再由递推式(21)有:
(28)
(29)
(30)
(31)
(32)
把式(26)~(32)代入式(14)就有θperiodic近似式:
(33)
(34)
(35)
3 数学模型的数值解方法
3.1 数值计算区域
用数值方法求解以上问题时选取整体区域并划分网格为如图2所示.

图2 整体计算时的网格Fig.2 Grid of total calculation
3.2 方程的变换[16]
将物理空间用适体坐标系转化到计算空间,如图3所示.
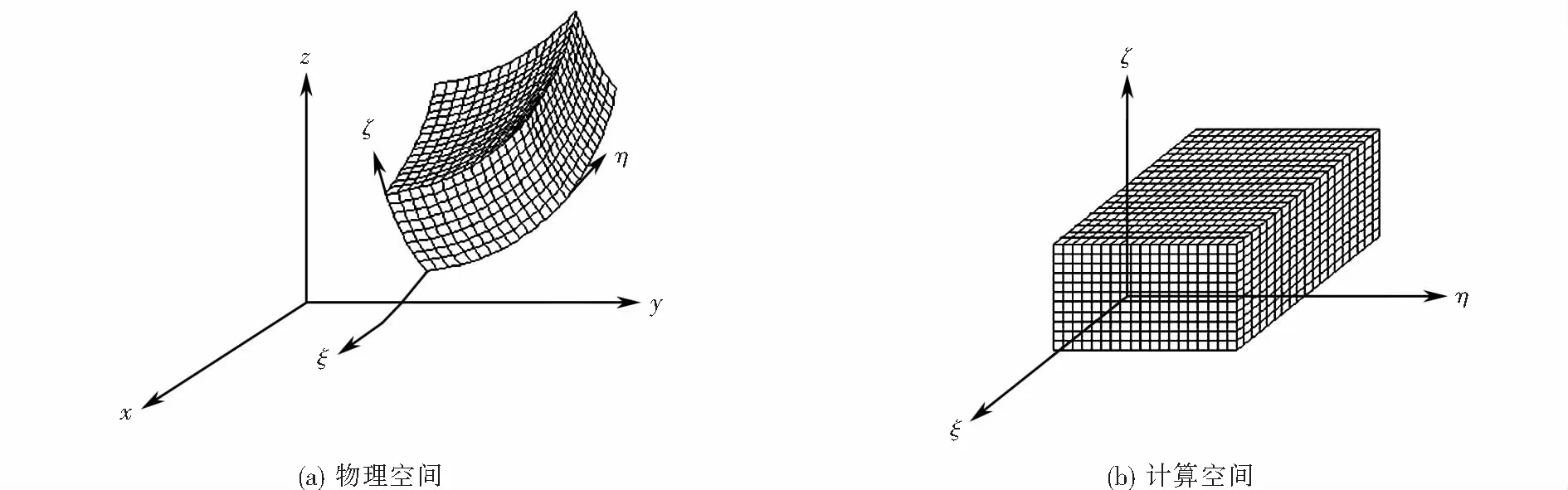
图3 适体坐标系的转换及控制容积Fig.3 Transformation and control volume of Body-Fitted coordinate system
令:
(36)
在计算空间方程(8)变换为:
(37)
3.3 方程的离散
以上方程可以图4所示的控制容积中离散.
aPθP=aEθE+aWθW+aNθN+aSθS+aTθT+aBθB+b.
(38)
方程离散后获得一个(L1-2)×(M1-2)×(N1-2)代数方程组及6个面上的边界代数方程.求解这一方程组,就可获得温度场.论文采用TDMA方法求解代数方程组.收敛判据是同一时层的迭代过程中最大温度相对误差不超过10-5.

图4 控制容积Fig.4 control volume
3.4 移动热源的处理方法
移动热源在数值计算过程中需特殊处理.如图5所示,把柱体侧面展开,AB线是同一条线,这时热源分布在AB周围及热源分布在两AB线之内.为保证计算过程中加入柱体的热量守恒,沿移动方向,每一时间步长热源移动一完整网格.

图5 计算区域移动热源分布示意图Fig.5 Distribution diagram of moving heat source in calculation area
4 结果及分析
4.1 计算用模型说明
图1模型和图2网格所示的圆柱半径为a=0.152 4 m.热源作用区为2φ0=π/10 rad,计算使用时间步长为Δt=0.001 s,α=4.415 955×10-6m2/s,λ=15.24 W/m·K,ω=10π,转一圈时间周期=2π/ω=0.2 s,无量纲时间周期为0.2α/a2=0.2×4.415 955×10-6/0.152 42=3.802 635×10-6.一个点从热源进入到退出所持续时间为φ0/ω=1/100 s.无量纲时间步长Δt*=0.001×4.416×10-6/0.152 42=1.901×10-7.圆柱表面对流传热系数h=1 000 W/m2·K,毕沃数NB=10.
4.2 解析解的特性
方程(13)第一项的特性如图6所示,其值随时间的变化规律为周期性变化.但其幅值不随时间变化.为了表明这一特性,我们把解析解第一项很长时间内θperiodic(周期性值)的变化如图6(a)所示.为了减小该图的字节数,图中只画出了三个较小时间段的温度波线.可以看出,θperiodic在较长时间段内的峰值变化并不明显.每一段的波线在图6(b)中放大.有图6(b)可知,波的幅值随时间变化非常小.

图6 解析解第一项(周期性值)随时间的变化规律Fig.6 The changes with time of first term (periodic value) of the analytic solution
方程(13)第二项(用θ2表示)的特性如图7所示,其数值和j的大小有关.方程(17)n=0的特征值μ0,j如表1所示.总体而言,无论j取何值,θ2的变化规律都是随时间的增加而逐渐增大的.随j的增大,θ2的初始值越小,增大的速度越快.当j>50时无量纲温度约接近数值解.
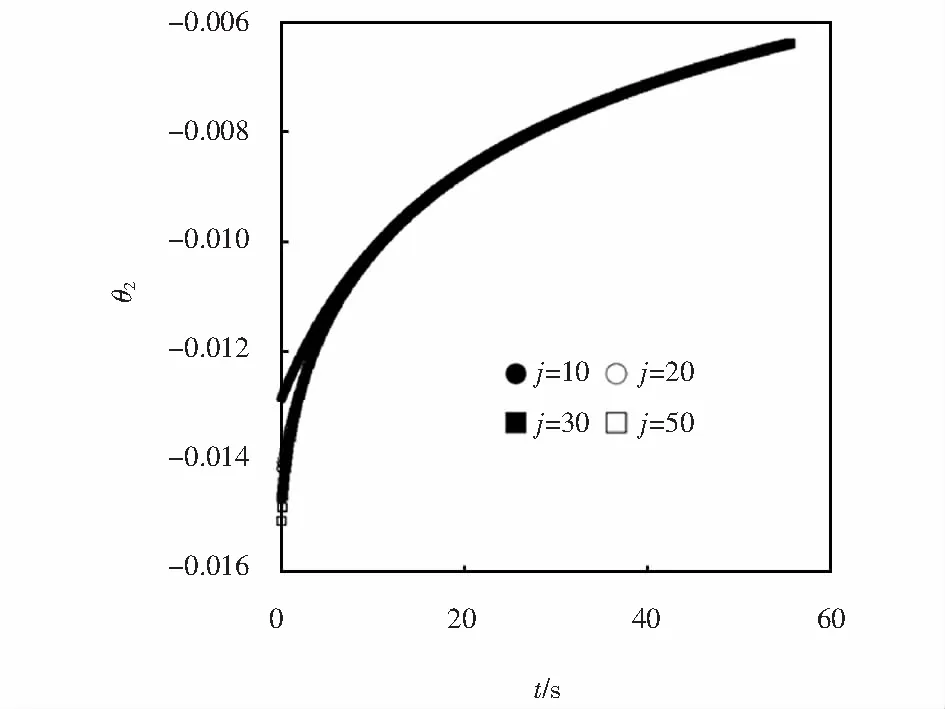
图7 解析解第二项(周期性值)随时间的变化规律Fig.7 The changes with time of second term (periodic value) of the analytic solution
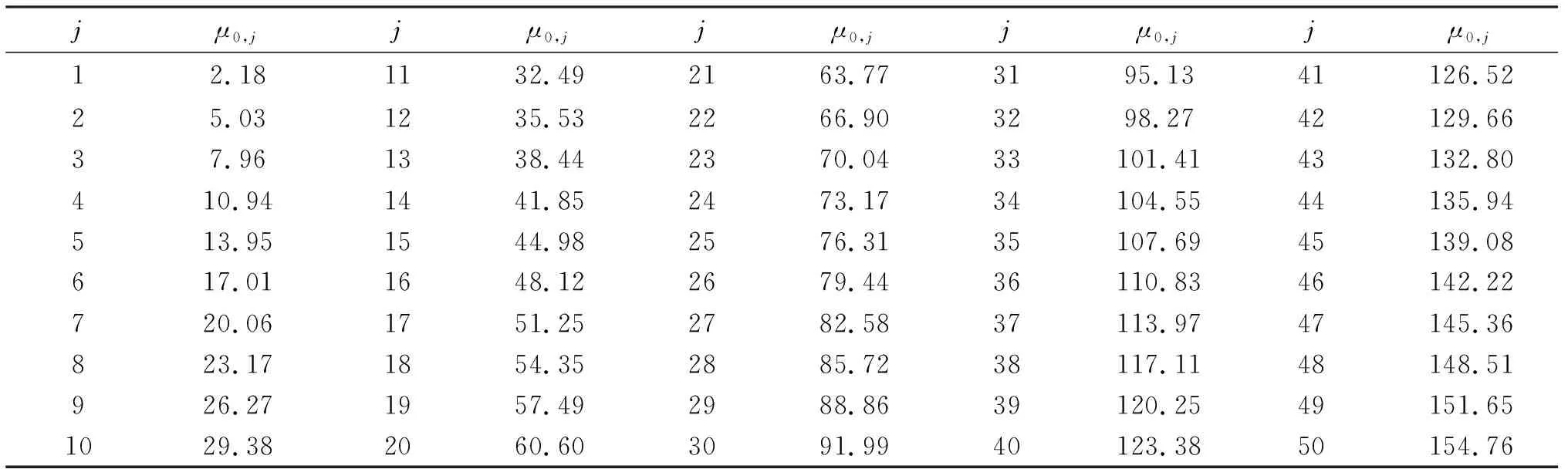
表1 特征值μ0,j的值
方程(13)第三项(用θ3表示)的特性如图8所示,其数值和j的大小有关.但相比θperiodic和θ2两项,其数量级较小,且仅在移动热源刚开始作用时刻有微小作用,随时间的增加,第三项数值减小为接近0,对方程(13)的几乎没有影响.
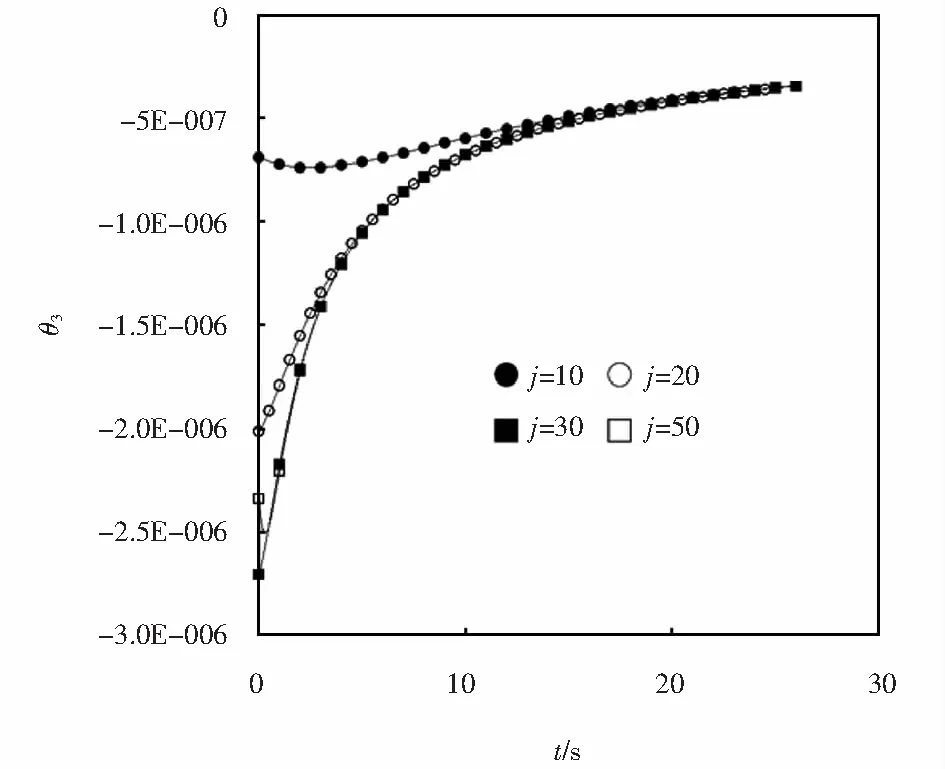
图8 解析解第三项随时间的变化规律Fig.8 The changes with time of third term of the analytic solution
解析解获得的圆柱侧表面一点无量纲温度随时间变化规律如图9所示.
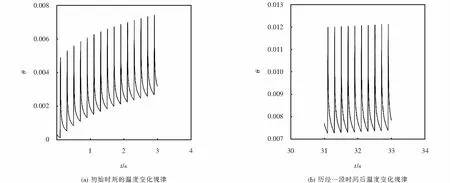
图9 圆柱侧表面一点无量纲温度随时间的变化规律Fig.9 Dimensionless temperature changing with the time of one point on the cylindrical side surface
无量纲温度在热源刚刚作用时跃升,热源刚离开的一段时间内骤降,温度下降到在较接近环境温度后,下降趋势减缓,热源再次作用时,无量纲温度再次上升.由于周期性运动,无量纲温度也呈现周期性规律.在无限长圆柱刚开始转动的时候,各个周期的最高温度随时间有升高的趋势,在运动一段时间后,热源造成的最大温升趋于稳定,可以看到侧表面温度随时间的变化为基本稳定的周期性规律,最高温度和最低温度基本为定值.
4.3 数值解与解析解的比较
1) 圆柱侧表面一点无量纲温度随时间变化规律的解析解与数值解对比
圆柱侧表面一点无量纲温度随时间变化规律的解析解与数值解对比如图10所示,无论是采用解析解还是数值解,得到的无量纲温度都具有相同的随时间变化的规律,且对比各个时刻的无量纲温度,两种方法的计算结果误差非常小.可以验证数值方法的准确性.
2) 同一时刻圆柱侧面无量纲温度分布的解析解与数值解比较
同一时刻圆柱侧面无量纲温度分布随位置变化的解析解与数值解比较如图11所示,可以看到,在同一时刻不同位置的无量纲温度存在着相似的变化规律.在热源作用区,无量纲温度突然上升并在即将离开热源作用区的位置达到最大值,越远离热源作用区,无量纲温度越低,其值减小的趋势越来平缓.但无论是采用解析解还是数值解,得到的无量纲温度都具有相同的随位置变化的规律,且对比同一时刻各个位置的无量纲温度,两种方法的计算结果误差非常小,验证了数值方法的准确性.
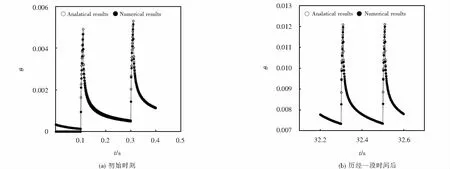
图10 圆柱侧表面一点温度随时间变化的解析解与数值解对比Fig.10 A comparison between the analytical results and numerical results of the temperature variation with time on the cylinder side surface
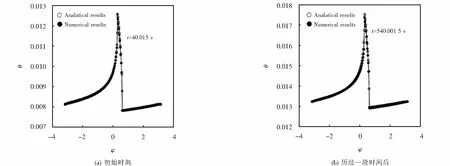
图11 同一时刻圆柱侧表面上无量纲温度随位置变化的解析解与数值解对比Fig.11 A comparison between the analytical results and numerical results of the dimensionless temperature variation on the cylinder side surface varies with position at the same time
5 结论
为了获得铁道车辆车轮在接近实际移动热源作用下的温度场,论文发展了一有限容积法数值方法程序,对该程序的准确性进行了验证.验证方法是用数值方法和解析方法解一无限长圆柱受一移动热源作用的温度场,比较两结果的差异.获得的结论如下:
1) 论文发展的采用有限容积法的程序获得的数值解和对应分析解相差甚小,程序计算结果准确性高,这说明发展的程序可以用来进行移动热源引起温度场的计算.
2) 解析解中第一项是随时间周期变化的,但其变化的幅值几乎不随时间的变化而变化.解析中第二项随时间是渐进增加的.第三项较第一及第二项小,在移动热源开始作用时刻有微小作用,随时间的增加,第三项数值减小为接近0.
3) 获得分析解的计算工作量不亚于数值方法的计算工作量,这与常规的认识有较大的出入.
