27.5 kV所用干式变压器谐波铜耗仿真研究

张荣秀，顾生杰,2，李 盼，田铭兴,2

(1. 兰州交通大学 自动化与电气工程学院，兰州 730070；2. 兰州交通大学 甘肃省轨道交通电气自动化工程实验室，兰州 730070；3. 中国铁路兰州局集团有限公司 兰州供电段，兰州 730000)

铁路系统所用干式变压器具有体积小、散热好、不易吸附灰尘等优点而逐渐广泛应用于所内低压用电设备供电[1].而目前运行中的27.5 kV所用干式变压器故障率较高，有时发生绕组、绝缘烧毁等事故，给电气化铁道安全运行带来了严重威胁.电气化牵引负荷具有随机波动大和非线性强的特点，使得接触网含有变化剧烈和丰富的高次谐波[2]，造成所用干式变压器及低压设备绝缘老化、寿命缩短，甚至烧毁.因此，有必要对牵引网产生的谐波对所用干式变压器铜耗的影响进行分析.

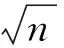
1 所用干式变压器三维模型建立

1.1 场路耦合模型

以某铁路开闭所一台型号为DC11-30/27.5的所用干式变压器为研究对象，利用Ansys Maxwell有限元软件建立其三维结构模型.为保证模型的精确度及仿真计算结果更符合实际，其中铁芯、绕组、空气间隙及绝缘树脂的厚度都是按照所用干式变压器的实际尺寸设置，并对场域模型做如下假设：

1) 由于绕组出线端、铁芯夹件对电磁场的影响较小，忽略不计，只建立铁芯、绕组和绝缘的结构模型；

2) 将铁芯简化成圆柱体；

3) 绕组中存在层间绝缘和匝间绝缘，建模时将绕组简化，低压绕组简化为3段3层，高压绕组简化为5段5层.

图1和表1是该所用干式变压器的二维平面示意图及结构参数，其型号为DC11-30/27.5，容量为30 kVA，绝缘等级为F级.

图1 所用干式变压器二维平面示意图Fig.1 Two-dimensional diagram of dry type transformer

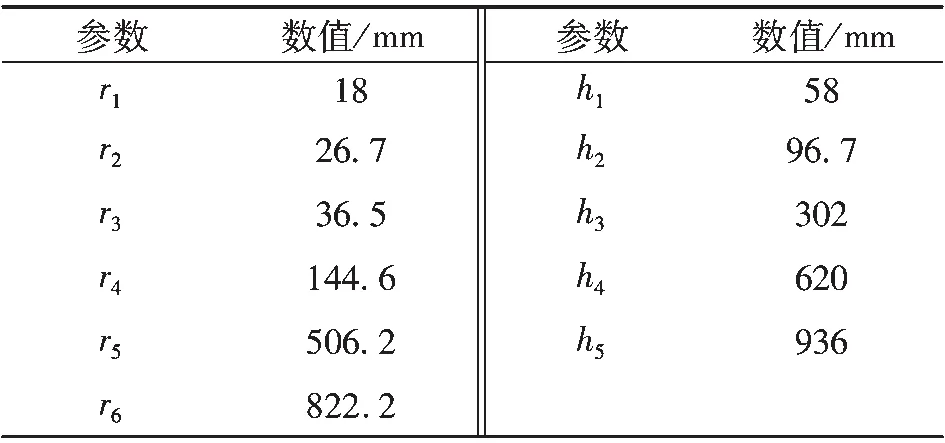
表1 所用干式变压器结构参数

本文以Ansys Maxwell为仿真平台，建立所用干式变压器的三维场路耦合有限元模型，对其联合仿真.所用干式变压器的三维场域模型如图2(a)所示.

所用干式变压器的激励由Maxwell的外电路编辑器加载，外电路模型如图2(b)所示，高压侧施加峰值为38 885 V的正弦交流激励，高压侧绕组电阻R1为148 Ω，低压侧绕组电阻R2为0.045 Ω，额定负载R为1 Ω，L1和L2分别为高、低压侧线圈，最终实现其场路耦合有限元仿真计算.

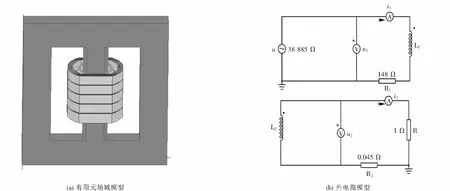
图2 仿真结构模型和外电路模型Fig.2 Screenshots of field model and circuit model

1.2 模型准确性验证

在所用干式变压器中，绕组电流产生的漏磁场将在绕组和各金属结构件中产生涡流损耗，这些损耗与绕组电阻损耗组成负载损耗.而涡流损耗在变压器金属结构件中分布不均匀，导致过热甚至局部过热；由于所用干式变压器高压侧畸变电压会渗透到低压侧[2]，导致绕组电流严重畸变，漏磁通也越来越大，损耗效应和热效应也明显：这些效应对所用干式变压器的性能影响较大，不可忽略，故对所用干式变压器进行漏磁场的分析尤为重要.

由图3可以看出：铁芯中最大磁通密度为1.640 7 T，绕组中部纵向漏磁通密度比较大，而在端部横向漏磁通密度较大；绕组中磁力线的一部分由于铁芯的磁特性在绕组端部向内弯曲，与铁芯部分的磁力线构成回路，另一部分向外，在空气中形成闭合回路.

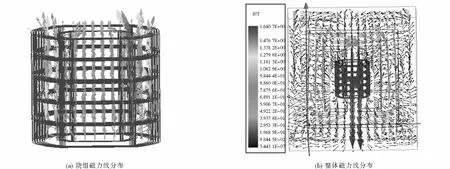
图3 t=0.1 s时所用干式变压器磁力线分布Fig.3 When t=0.1 s,the magnetic force line distribution of dry type transformer

为验证建立的27.5 kV所用干式变压器模型的精确度，对三维有限元模型电磁场进行分析，以一、二次侧电压、电流、空载损耗和负载损耗6个指标对比变压器铭牌参数，验证模型的准确性.所用干式变压器在额定工况下，仿真得到额定电压、额定电流、负载损耗；空载工况下得到空载损耗.从表2可以得出：仿真值与试验值存在一定误差，这主要是因为所用干式变压器模型为简化结构，但仿真值与理论值误差不超过6%，验证了该三维模型的正确性.

虽然意识形态虚假性常常被解读为统治阶级在主观上对民众进行的有意欺骗，但是这并不是马克思的原意。基于《路易·波拿巴的雾月十八日》《1848年至1850年的法兰西阶级斗争》等重要著作，不难看出，马克思通过回顾法国革命中资产阶级从革命力量蜕变为保守甚至反动力量的历史，揭示出意识形态围绕着社会利益关系，经历了一个从真实到虚假的历史演变过程，意识形态虚假性问题则是这一过程的必然产物，不以人们的主观意志为转移㉗。这揭露出意识形态利用群众、欺骗群众的伪群众性特征，这也成为剥削阶级占据统治地位的阶级社会意识形态虚假性的突出表现之一。

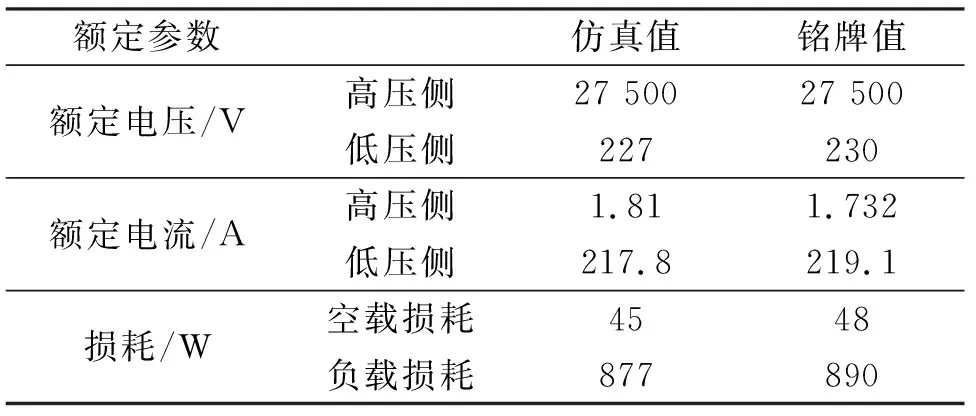
表2 所用干式变压器仿真值与铭牌值对比

2 谐波损耗特性分析

2.1 集肤效应及邻近效应影响下的谐波铜耗

由法拉第电磁感应定律可以知道，当交流电通过导体时将会在导体周围产生交变磁场，而这个交变磁场会在导体内部产生涡流，改变导体内部的电流密度分布，使电流趋于导体表面，从而减小导体的有效截面积，因此绕组交流电阻增加.

当所用干式变压器工作在高频谐波环境下，因集肤效应和邻近效应导致绕组中电流密度分布更不均匀[7-8]，使绕组的实际电阻大于直流电阻而不能忽略，且电流频率越高，集肤效应越明显.文献[9]提出了交流电阻的集肤效应系数ksh为绕组的交流电阻与直流电阻的比值，即

(1)

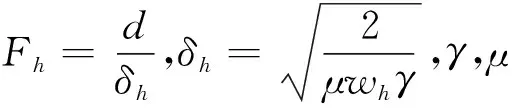
在谐波存在的情况下计算谐波铜耗时，考虑到不同频率谐波的正交性，将各次谐波损耗以及直流电流的损耗求和[10]，得到绕组在谐波条件的铜耗

(2)

IEEE计算谐波铜耗公式为

(3)

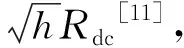
从图4可以看出：当谐波频率较低时，两种方法计算结果接近；随着谐波频率增大，两种方法计算结果相差越大；高频下，集肤效应和邻近效应对绕组铜耗的影响较大，不可忽略.

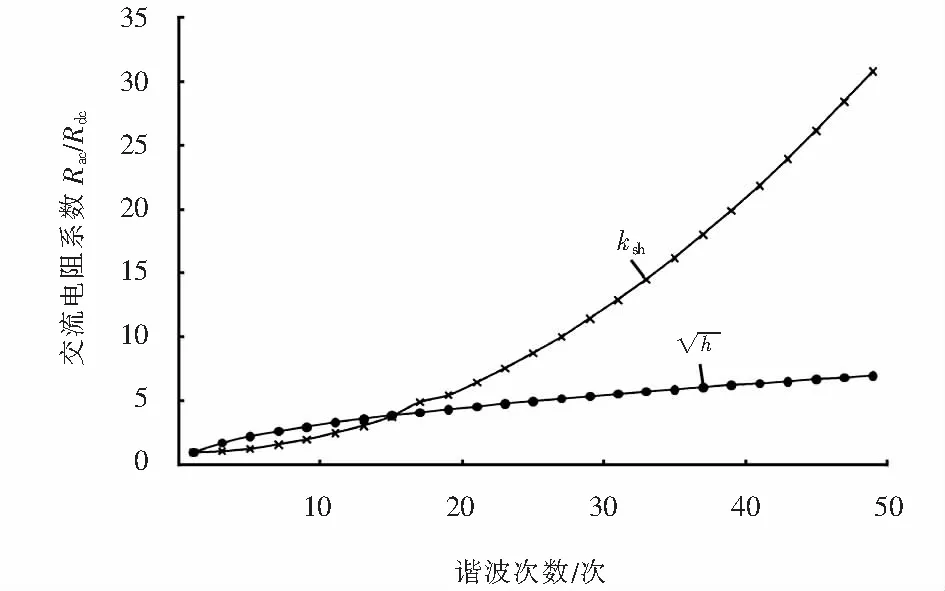
图4 两种方法计算值对比Fig.4 Comparison of calculated values between the two methods

2.2 谐波损耗叠加性仿真验证

以上谐波铜耗的分析计算都是假设其满足叠加性的前提下进行的.由于集肤效应和邻近效应的影响，不同频率的电流在铜导线截面的电流密度分布是不同的，在谐波电流背景下，总的功率损耗是否可以视为各次谐波单独存在时产生损耗的线性叠加，本文对此进行验证.

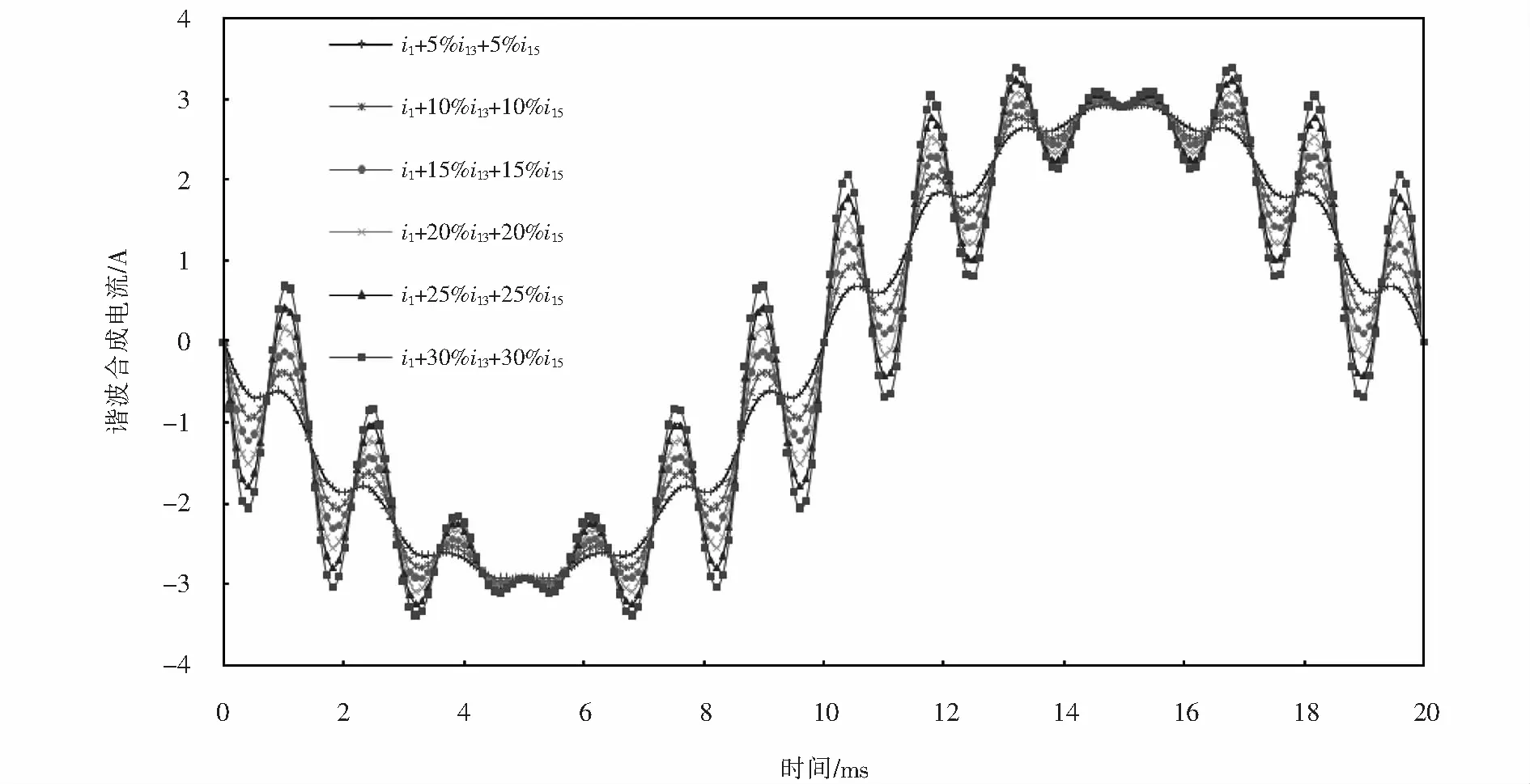
图5 基波叠加不同含量的13次和15次谐波电流的合成电流Fig.5 Synthetic current of fundamental waves superimposed with different levels of 13th and 15th harmonic currents

将合成谐波电流和单次谐波电流造成的总谐波铜耗进行对比(见表3和图6)，验证谐波损耗的叠加性.由表3和图6谐波铜耗对比可以看出：复合次谐波电流流过所用干式变压器时产生的谐波铜耗与单次谐波电流通过所用干式变压器时产生的谐波铜耗基本相同，偏差率在5%以内，说明了复合次谐波背景下绕组中产生的损耗与其单独存在时一致，与文献[8,12]理论推导结果一致，验证了谐波损耗的可叠加性.

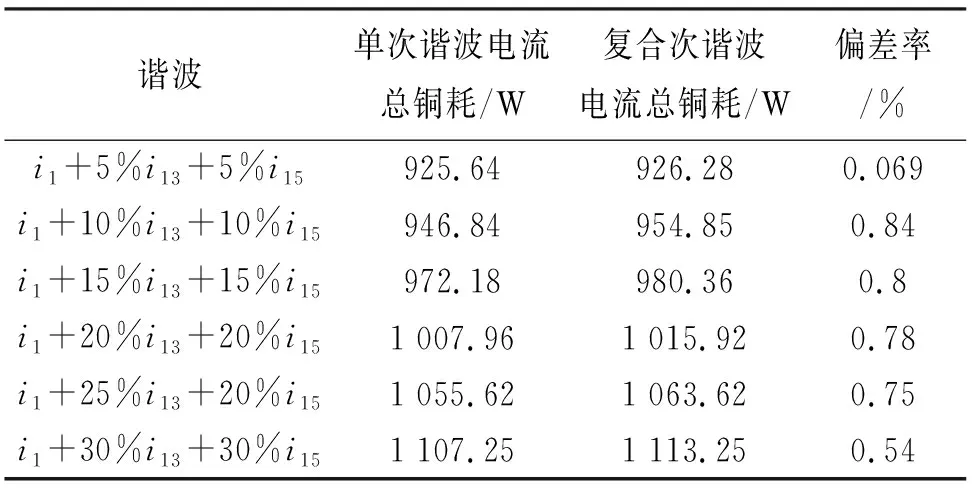
表3 单次谐波与复合次谐波电流时谐波总铜耗对比

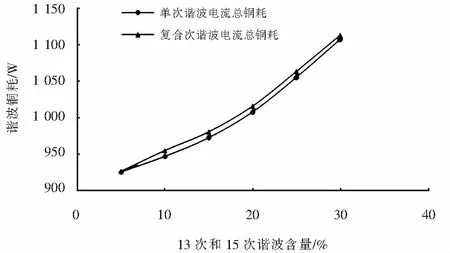
图6 单次谐波与复合次谐波电流下的谐波铜耗对比曲线Fig.6 Comparison curve of harmonic copper consumption under single harmonic and compound harmonic c- urrents

2.3 谐波电流对所用干式变压器谐波铜耗的影响

谐波情况下变压器谐波铜耗占谐波总损耗的主要部分[13]，因此精确计算谐波电流对所用干式变压器的谐波铜耗的影响，对其结构优化有重要意义[14].在所用干式变压器外电路模型高压侧加载不同谐波含量及谐波次数下的电流源激励，将运行所得数据储存到StrandedLoss单元，计算周期内的平均谐波铜耗.表4是谐波铜耗与谐波电流含量及谐波次数变化的定量关系，并根据表4绘制图7、图8所示的谐波铜耗随着谐波电流含量及谐波次数变化的关系曲线.

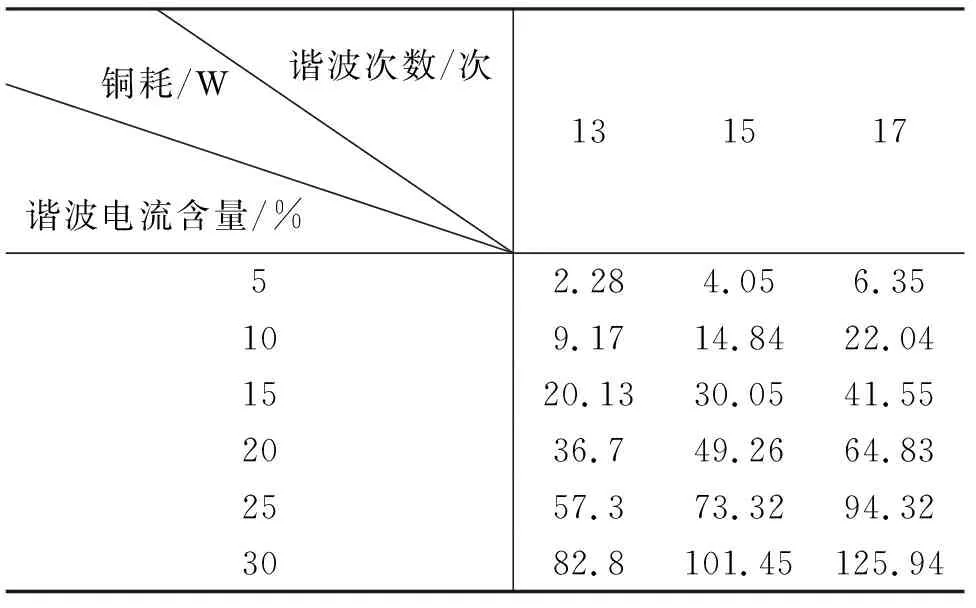
表4 不同谐波次数、谐波电流含量下的谐波铜耗

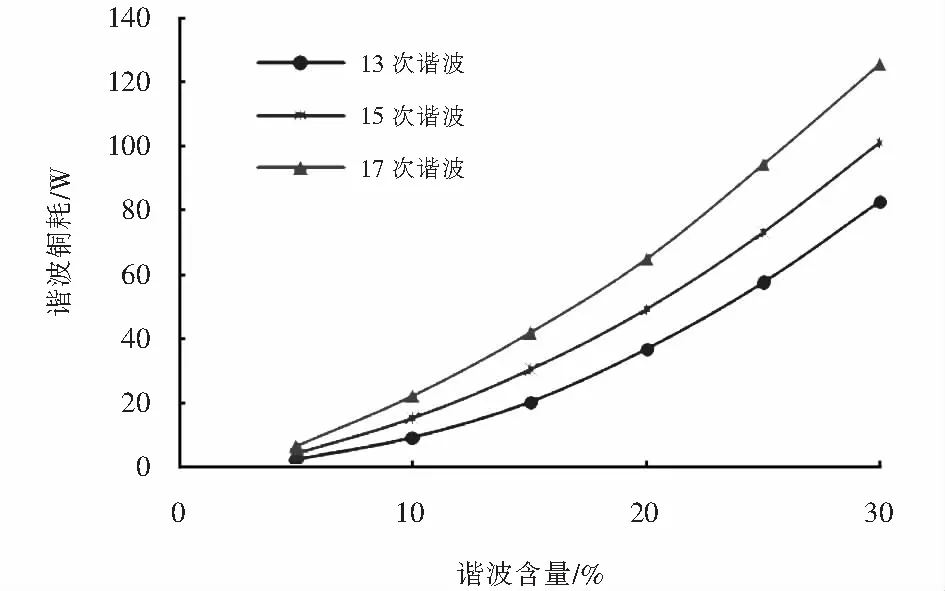
图7 谐波铜耗和谐波含量的关系曲线Fig.7 Curve of the harmonic copper consumption and harmonic current content

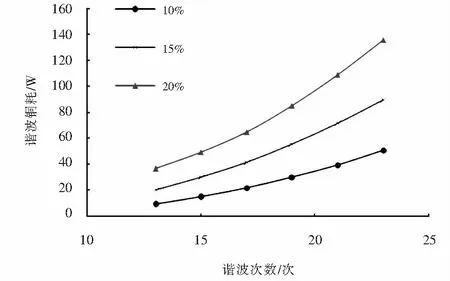
图8 谐波铜耗和谐波次数关系曲线Fig.8 Curve of the harmonic copper consumption and harmonic current number

由图7和图8可以看出：当谐波电流次数一定时，谐波铜耗与谐波电流含量的平方成正比；当谐波电流含量一定时，谐波铜耗随着谐波电流次数的增加而增加，这与交流电阻集肤效应系数波形上升趋势一致，谐波电流次数越大，谐波铜耗增加的越多，这主要是因为绕组受到集肤效应和邻近效应的影响使得有效电阻增加，而集肤深度又与频率成反比关系.

根据图7和图8绘制出所用干式变压器的谐波铜耗随谐波含量及谐波次数变化的关系，如图9所示.

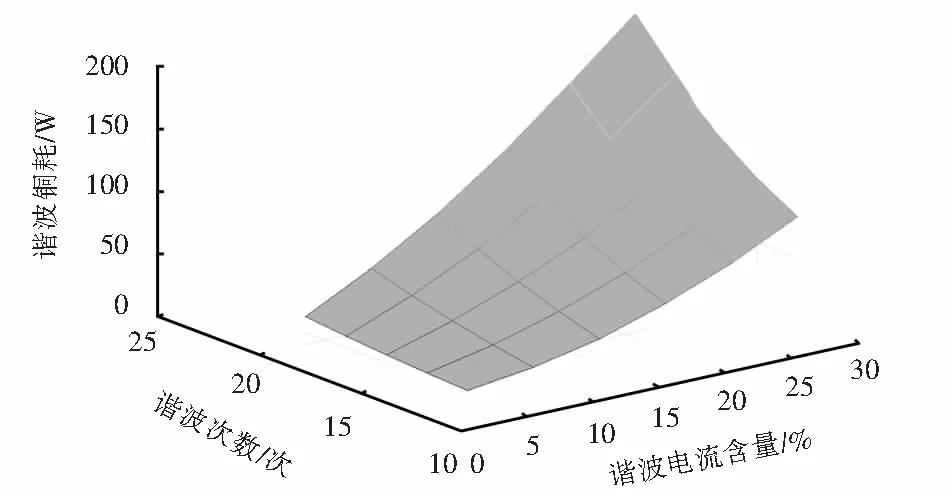
图9 谐波铜耗与谐波含量及谐波次数的关系Fig.9 Relationship between harmonic copper loss, harmonic current content and harmonic cu- rrent number

3 实例分析

3.1 牵引供电系统仿真建模

本节以韶山VI(SS6B)交直型机车和CRH系列(CRH2)动车组为例，在Matlab/Simulink环境下建立牵引供电系统仿真模型，对SS6B交直型机车和CRH2交直交型机车混跑时，牵引网中谐波渗透到所用干式变压器高压侧的谐波特性进行仿真分析[15].仿真中，所用干式变压器为单相双绕组变压器，将其安装于供电臂中间的AT所内.将一次绕组的两端分别接入牵引网接触线与钢轨，二次绕组连接所内用电负荷[16].一次侧电压设置为27.5 kV，二次侧电压设置为0.23 kV，并设置高压侧绕组电阻为148.062 Ω，电感为1.6 H，低压侧绕组电阻为0.045 Ω，电感为0.17 mH.牵引供电系统仿真模型如图10所示.

3.2 仿真结果

图10的仿真模型运行0.2 s后得到所用干式变压器高压侧的谐波电压、电流，如图11所示，并将电流波形进行傅里叶分解得到图12电压频谱图，电压、电流波形的不平滑主要是整流逆变装置谐波产生的影响.

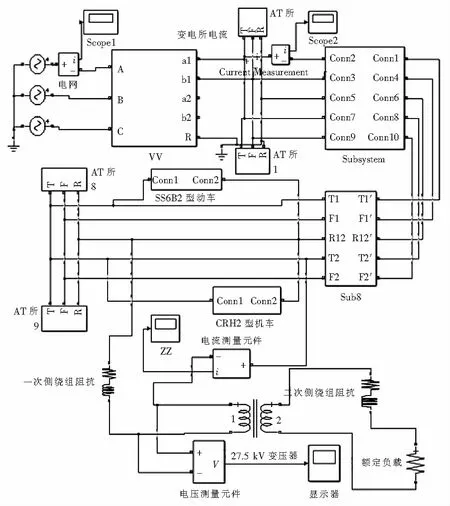
图10 系统仿真模型Fig.10 System simulation model

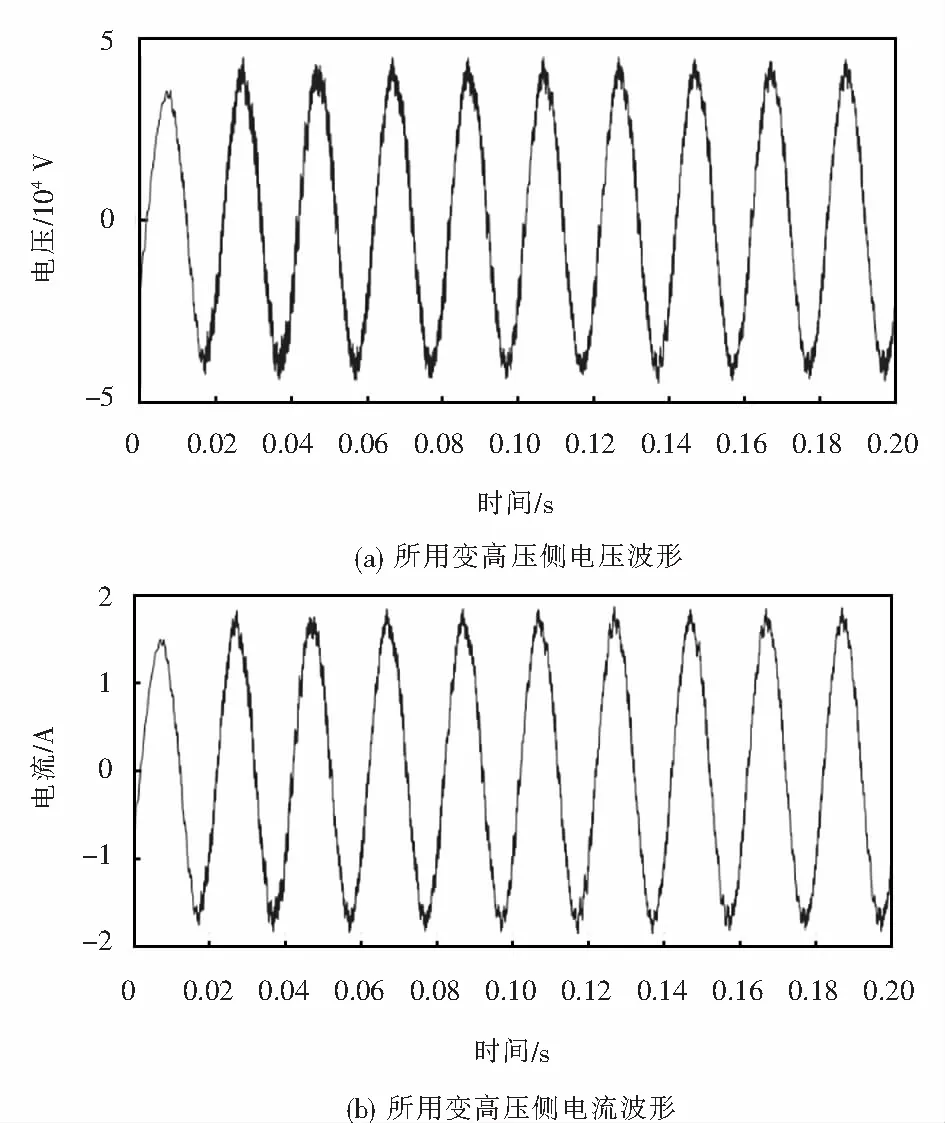
图11 两车混跑时所用干式变压器高压侧电压与电流 波形Fig.11 Waveform of voltage and current at high voltage side of dry type transformer when two vehicles run together

从图12可以得到，SS6B型和CRH2机车混跑时，电流畸变率为8.06%.从图12可以看出：此时高压侧电流中5次、11次、15次和19次低次谐波与45次、49次、51次、55次高次谐波占主要成分，且51次谐波含量最高，可达到5.9%；机车产生的谐波主要以奇次谐波为主，偶次谐波含量较少.所用干式变压器高压侧电压、电流波形畸变和机车负荷的非线性、冲击性有关.

图12 所用变高压侧电压频谱图Fig.12 High voltage current spectrum of dry type transformer

将所用干式变压器高压侧加谐波电压，低压侧加谐波电流，得到所用干式变压器的谐波铜耗为925 W，谐波铁耗为55.53 W；谐波电压、电流情况下，所用干式变压器的谐波铜耗与基波铜耗相比增加了5.47%(基波铜耗为877 W)，谐波铁耗与基波铁耗相比增加了23.4%(基波铁耗为45 W).长期处于谐波电流情况下，所用干式变压器增加的铜耗以热能的形式表现，持续增加的热能在变压器内部传递将导致其绝缘寿命下降，最终会造成所用干式变压器发生故障.

4 结论

基于场路耦合法，建立所用干式变压器的三维仿真模型，考虑集肤效应和邻近效应对绕组谐波铜耗的影响，利用有限元分析所用干式变压器在谐波电流下绕组中谐波铜耗的变化规律；搭建牵引供电系统仿真模型，分析实际运行工况下所用干式变压器的谐波铜耗，得到以下结论：

1) 证明了所用干式变压器谐波铜耗的可叠加性.单次谐波电流对所用干式变压器谐波铜耗的影响与复合次谐波电流对谐波铜耗的影响相同，验证了所用干式变压器谐波铜耗的可叠加性.

2) 所用干式变压器的谐波铜耗与谐波电流含量、次数有关.谐波电流次数一定时，谐波铜耗与谐波电流含量的平方成正比；由于集肤效应和邻近效应对谐波铜耗的影响，当谐波电流含量一定时，谐波铜耗随着谐波电流次数的增加而增加，且谐波电流次数越大，谐波铜耗增加的越多.

3) 牵引供电系统谐波电压、谐波电流会渗透到所用干式变压器中，且45次、49次、51次、55次高次谐波电压、电流成分较多，造成所用干式变压器谐波铜耗增加的更多.