虚拟同步发电机下垂特性与控制模型阻尼系数的关系
2022-04-26邢东峰田铭兴
邢东峰,田铭兴
(1. 兰州交通大学 自动化与电气工程学院,兰州 730070;2. 兰州交通大学 甘肃省轨道交通电气自动化工程实验室,兰州 730070;3. 兰州交通大学 甘肃省高原交通信息工程及控制重点实验室,兰州 730070)
电力系统的稳定性是电力系统运行控制考虑的首要问题,尤其是电力系统频率的稳定至关重要.传统电网频率控制主要通过一次调频和二次调频实现,特别是由发电机自动实现的一次调频[1],是实时自动的调频方法,不但实现了频率的稳定控制,而且实现了发电机功率的分配,从而实现电力系统动态功率稳定[2].一次调频方法的本质是频率-功率的下垂控制[3-6].虚拟同步发电机(virtual synchronous generator,VSG)控制[7]通过电力电子设备的控制模拟传统同步发电机的特性,常用于可再生能源的发电并网.由于其并网特性友好,成为新能源发电的研究热点.VSG模拟传统同步发电机的同时,一般也具有下垂特性[8-9].
目前很多学者针对VSG的下垂特性进行了研究,其中:以文献[10-12]为代表的第一种VSG模型阻尼项设置以初始频率为参照,实现自同步特性;以文献[13]为代表的第二种VSG模型的阻尼项设置以电网频率为参照,实现与电网的同步特性.基于此,文献[10]分析了第一种VSG的下垂特性与调差系数的关系;文献[11-12]给出了第一种VSG模型的下垂系数与阻尼系数的关系式,特别是文献[14]还利用了两种模型的下垂特性,通过两种模型的切换实现二次调频;综述性文献[15]也提到,大多数VSG技术的下垂特性是通过阻尼系数反映的,即同步发电机的下垂特性,除了受一次调频调节器的影响,同时受阻尼绕组产生的阻尼系数的影响.
虽然上述有些文献也涉及第一种VSG模型的下垂特性和阻尼系数的关系,但是在不同的模型中,VSG参数对下垂特性的影响是不一样的,所以分析不同VSG模型的阻尼系数和下垂特性的关系,给出具有不同阻尼项VSG的下垂特性关系式是有必要的.本文从下垂特性的角度入手,对比分析不同VSG模型的下垂特性与阻尼系数的关系.
1 VSG下垂特性原理
同步发电机一般具有下垂特性.其下垂系数定义为
(1)
其中:Kpi为第i台发电机的下垂系数,单位为W/Hz;ΔPGi=PGi-PGi0为第i台发电机的功率变化量,PGi和PGi0分别为第i台发电机的实时功率和初始功率,单位W;n表示整个电力系统中发电机的数量;Δωgcc=ωgcc-ωgcc0为电网频率变化量,ωgcc和ωgcc0分别是电网实时频率和初始频率.整个电力系统发电机的发电功率变化量ΔPGs=PGs-PGs0,PGs和PGs0分别为整个电力系统发电机的总实时功率和总初始功率.则有
(2)
可得整个电力系统发电机的总下垂系数
(3)
电力系统负荷增加ΔP或发电功率减少ΔP时可以通过一次调频实现电力系统发电功率与负荷之间新的平衡:ΔPGs-ΔP=0,即
-KpsΔωgcc-ΔP=0.
(4)
由式(4)可得
(5)
发电机i输出功率变化量为
(6)
通过式(5)可以看出:负荷变化ΔP时,发电机总下垂特性Kps越大,则电网频率变化Δωgcc越小.通过式(6)可以看出:各发电机可以通过不同的Kpi系数,根据自身的调节能力和需求对维持频率稳定做出不同的贡献,实现无需发电机间统一控制的自动功率分配.
同步发电机的下垂特性,一般通过一次调频调节器实现.VSG模拟同步发电机的方式不尽相同,其下垂特性有时跟阻尼系数有关.
2 VSG下垂特性与阻尼的关系
同步发电机常用的二阶运动方程如下:
(7)
其中:KJ为同步发电机惯性系数,单位为kg·m2;Ω为转子角速度;Ωref为发电机参考角速度;Tm,Te,TD为机械转矩、电磁转矩和阻尼转矩;Pm,Pe表示输入机械功率和输出电磁功率;KD为阻尼系数,单位为W·s.
目前大多数VSG模型都是仿照式(7),大致相同,主要区别在于阻尼项.多数模型将同步发电机的Ωref对应于VSG的初始频率ω0,这些模型以ω0为参考,不需采集电网频率,算法简单且可用于VSG单机离网运行控制.还有一种模型以电网实际频率为参照,需采集电网实际频率,适于VSG并网运行控制.两种阻尼项[16]可以写为KDω0(ω-ω0)和KDω0(ω-ωgcc).定义Δω=ω-ω0(ω为VSG实时角频率)和Δωgcc=ωgcc-ωgcc0(假设初始状态为稳态,有ωgcc0=ω0),所以上述两个阻尼项也可分别写成KDω0Δω和KDω0(Δω-Δωgcc).据此可以得到三种VSG基本控制模型:
1) 模型Ⅰ:阻尼项为KDω0Δω的VSG控制模型.
2) 模型Ⅱ:阻尼项为KDω0(Δω-Δωgcc)的VSG控制模型.
3) 模型Ⅲ:增加下垂控制环节的阻尼项为KDω0
(Δω-Δωgcc)的VSG控制模型.
2.1 模型Ⅰ的下垂特性
模型Ⅰ传递函数为
ΔPin-ΔPG=KJω0(sΔω)+KDω0Δω,
(8)
其中:ΔPin=Pin-Pin0为VSG输入功率扰动量,Pin和Pin0分别表示VSG的实时输入功率和初始输入功率;ΔPG=PG-PG0为VSG输出功率扰动量,PG和PG0分别表示VSG的实时输出功率和初始输出功率.
根据文献[17]可得
(9)
其中:KS为VSG同步系数,单位为W/Hz,
(10)
其中:U0为VSG输出相电压有效值;Ugcc为电网相电压有效值;δ0为VSG初始功角;L为VSG并网传输线等效电感.
根据式(8)和式(9)可以得到VSG小信号分析模型框图,也可以称为Phillips-Heffron模型(简称P-H模型)[18].模型以初始频率为参照实现自同步,故此称为自同步VSG模型,如图1所示.
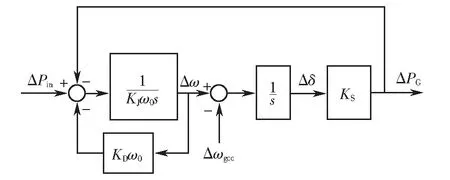
图1 VSG模型ⅠFig.1 VSG model Ⅰ
令ΔPin=0,则根据图1可得传递函数
(11)
如果系统是稳定的,根据终值定理可得式(11)的稳态值为
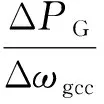
(12)
对比式(1)和式(12)可以看出:对应发电机下垂系数
Kp=KDω0.
(13)
2.2 模型Ⅱ下垂特性
有些VSG设计时将KDω0(ω-ω0)改为KDω0(ω-ωgcc),基本方程如下:
ΔPin-ΔPG=KJω0(sΔω)+KDω0(Δω-Δωgcc).
(14)
根据式(9)和式(14)可以得到VSG小信号分析模型框图,如图2所示.

图2 VSG模型ⅡFig.2 VSG model Ⅱ
令ΔPin=0,则根据图2可得传递函数
(15)
如果系统是稳定的,根据终值定理可得式(15)的稳态值为
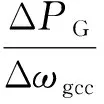
(16)
对比式(1)和式(16)可以看出:VSG的下垂系数为
Kp=0.
(17)
所以模型Ⅱ不具有下垂特性,阻尼系数KD影响过渡过程,未实现下垂特性,一般应用时需要另外增加下垂控制环节,由此得到模型Ⅲ.
2.3 模型Ⅲ的下垂特性
模型Ⅲ如图3所示.
令ΔPin=0,则根据图3可得传递函数
(18)
如果系统是稳定的,根据终值定理可得式(18)的稳态值为
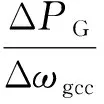
(19)
对比式(1)和式(19)可以看出:模型Ⅲ的下垂系数为Kp.显然,当图3所示模型Ⅲ的Kp设置为0时,与图2中的模型相同.
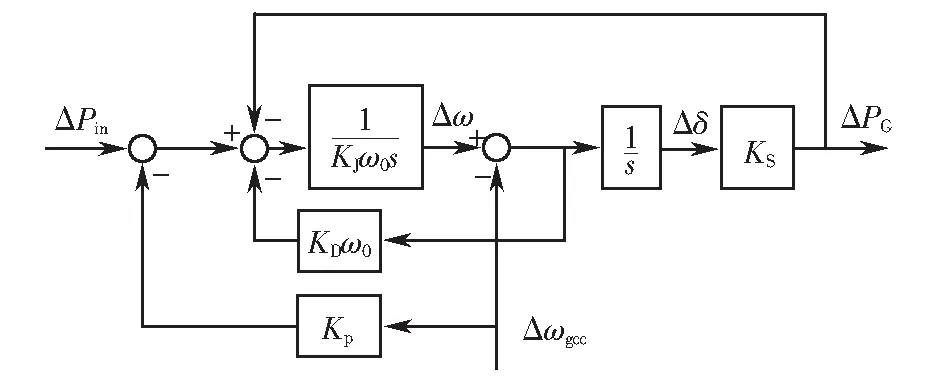
图3 VSG模型ⅢFig.3 VSG model Ⅲ
对比2.1~2.3节的内容可以看出:三种模型的下垂特性是不一样的,尤其是阻尼系数对下垂特性的影响是不同的.由式(13)可见:模型Ⅰ的的下垂特性和阻尼系数成正比,这意味着阻尼系数越大,系统下垂系数越大,输出功率扰动时VSG频率变化越小,电网频率扰动时功率变化越大.由式(17)可见:模型Ⅱ的下垂系数总为0,与阻尼系数无关,这意味着该模型在电网频率扰动时,输出功率不变,无法实现功率扰动时发电机的自动功率分配,不能自动地进行一次调频.模型Ⅲ可以独立地设置系统阻尼系数和下垂系数,比模型Ⅰ更灵活,可单独设置下垂系数Kp的值.
3 VSG仿真控制模型和参数
为实现VSG仿真,建立图1~3三种VSG的仿真控制电路模型.VSG仿真电路主要包括逆变主电路和控制器.由控制器检测输出电压、电流以及指定输入功率,并产生PWM控制信号,控制逆变主电路.VSG仿真电路结构如图4所示.
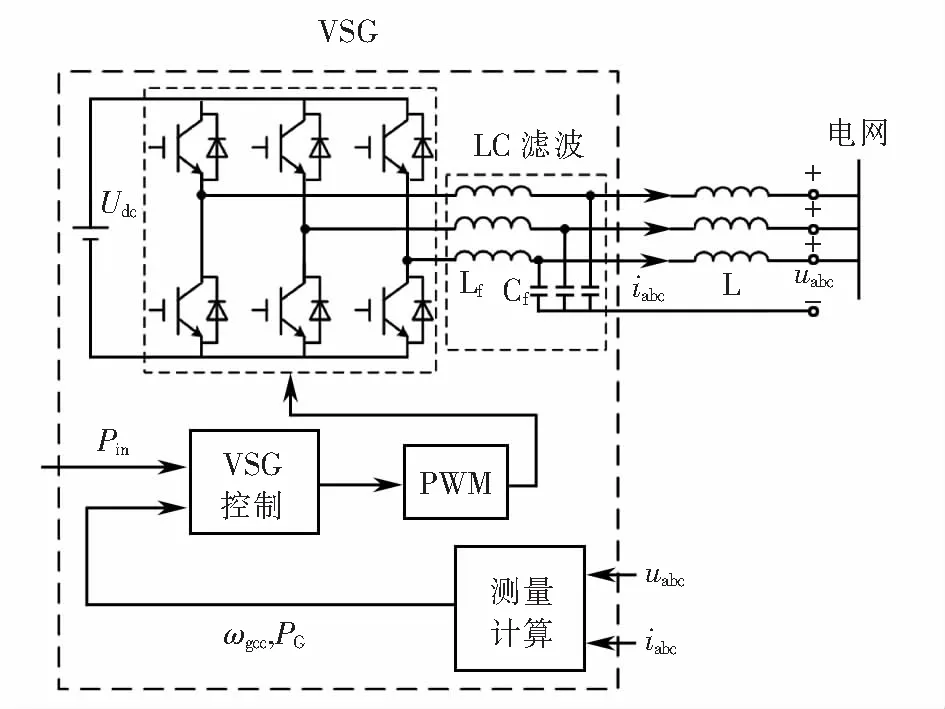
图4 VSG仿真模型Fig.4 VSG simulation model
图4中,Pin为VSG的输入功率,uabc表示电网三相相电压瞬时值,iabc表示电网三相线电流瞬时值,Udc表示VSG输入直流母线电压值.VSG控制分别采用图1、图2和图3的控制模型Ⅰ、模型II和模型III.为了简化分析,暂不考虑VSG的无功控制.
电力系统拓扑结构种类繁多,总体上可分为大电网和微电网两种.VSG并入大电网时,其对电网整体功率和频率的影响可以忽略,需要分析的是电网频率变化时VSG的响应.VSG应用在微电网场合时,其对系统的频率和功率平衡影响都很大,同时为了研究功率在发电机间的分配,因此以双机并联离网运行为代表进行分析.所以仿真案例选择VSG单机并网和双机并联离网两种运行场景:单机并网时可认为电网功率无穷大,VSG输出功率由VSG本身决定,可以研究电网频率变化时的VSG下垂特性;双机并联离网时两台VSG输出总功率由负荷决定,可以研究负荷功率变化时两台VSG的功率分配以及下垂特性.VSG仿真参数[19]见表1.
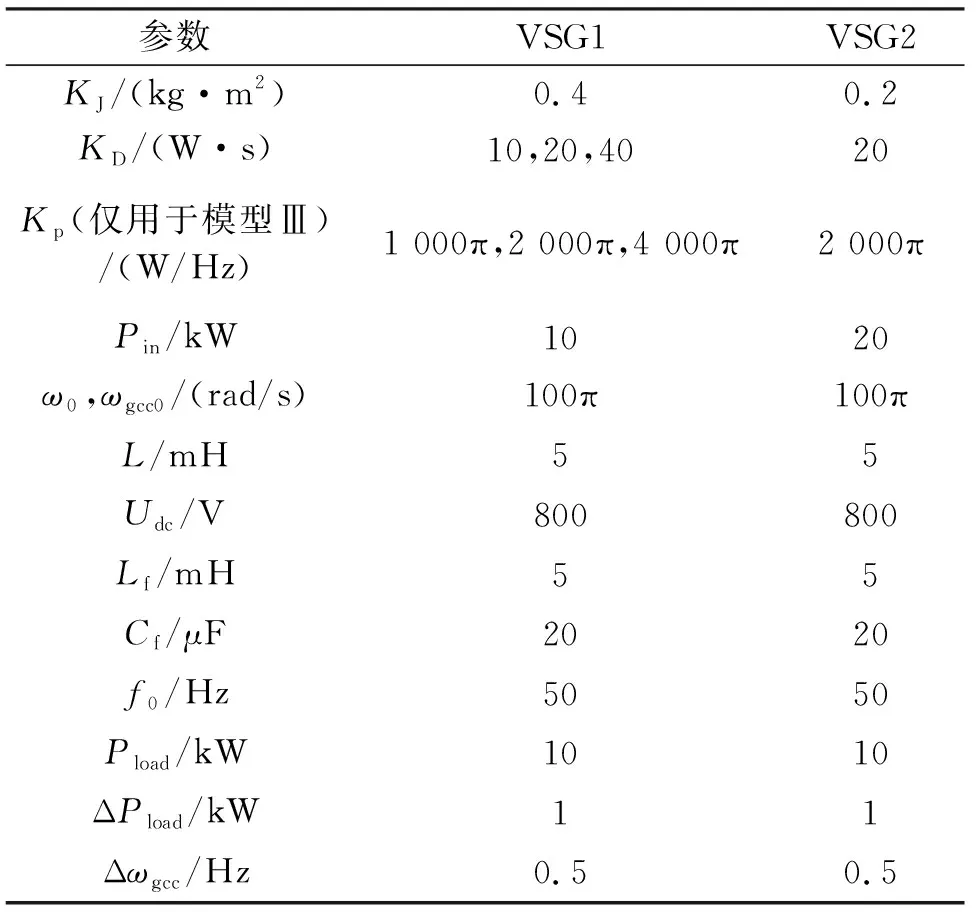
表1 VSG参数
4 仿真案例和分析
4.1 单机并网运行仿真
当VSG接入无穷大电网时,VSG的输出功率远远小于整个电网的负载功率,此时可以通过三相电压源模拟电网,其三相线电压有效值为380 V,初始频率为额定频率(50 Hz),在t=1.5 s时模拟电网频率扰动改变为50.5 Hz.并网运行仿真模型如图5所示.
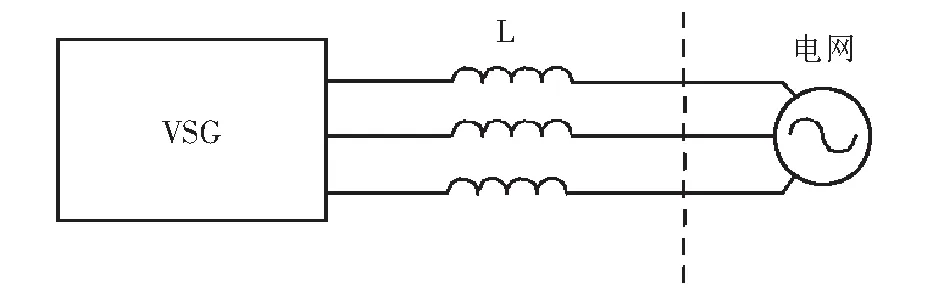
图5 VSG并网运行仿真模型Fig.5 Gird connected VSG simulating model
VSG控制采用模型Ⅰ,并分别采用表1中VSG1参数KD的3个值,仿真结果如图6所示.
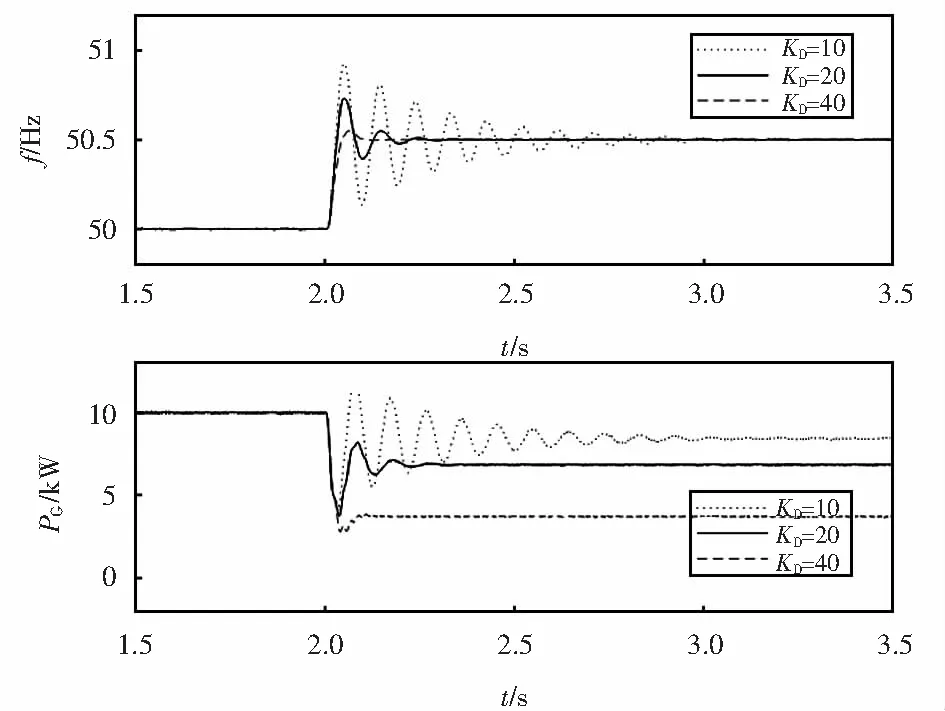
图6 模型Ⅰ并网运行仿真结果Fig.6 Gird connected simulating results of model Ⅰ
VSG控制采用模型Ⅱ,并分别采用表1中VSG1参数KD的3个值,仿真结果如图7所示.
VSG控制采用模型Ⅲ,选Kp=2 000π W/Hz,采用表1中VSG1参数KD的3个值,可得仿真结果图8(a);选KD=20 W·s,采用表1中VSG1参数Kp的三个值,可得仿真结果图8(b).
由图6可见:阻尼系数越大,电网频率扰动后过渡过程频率和功率振荡越小,稳定后功率变化越大,这正好与式(13)相符,阻尼系数越大,VSG的下垂系数越大.从图7可以看出:电网频率扰动,稳定后的功率没有变化,这与式(17)相符,VSG下垂系数等于0,与阻尼系数无关,阻尼只是影响过渡过程,阻尼系数越大,振荡越小.由图8(a)可以看出:电网频率扰动后功率可以达到一个稳定值,该稳定值正好是图6中阻尼系数为20 W·s时的稳定值(这是因为此时模型III增加的下垂系数正好等于模型Ⅰ阻尼系数为20 W·s时的下垂系数),且与阻尼系数无关,这与式(19)相符,VSG的下垂系数为给定值,而阻尼系数只影响过渡过程,这又和模型Ⅱ一致.由图8(b)可以看出:当模型ⅢKp与模型Ⅰ的KDω0相等时,在相同的电网频率扰动下,新的稳态ΔPG相同.
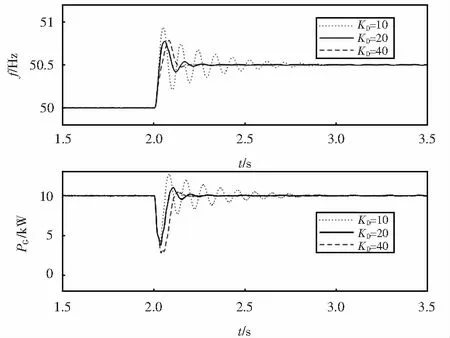
图7 模型Ⅱ并网运行仿真结果Fig.7 Gird connected simulating results of model Ⅱ
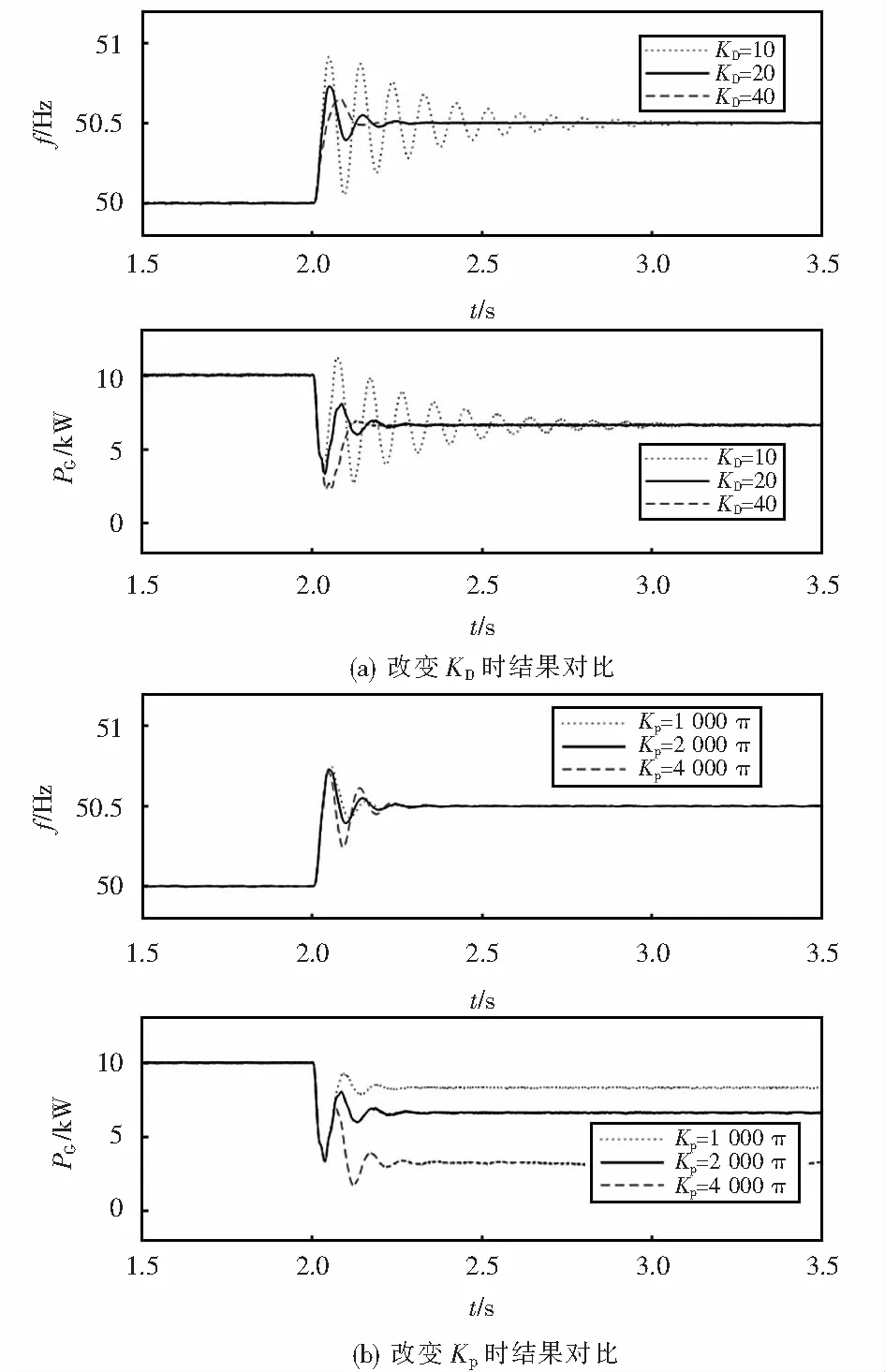
图8 模型Ⅲ并网时运行仿真结果Fig.8 Gird connected simulating results of model Ⅲ
总的来说,模型Ⅰ的下垂特性由阻尼系数决定,模型Ⅱ不具有下垂特性,模型Ⅲ的下垂特性由给定的下垂系数决定,与阻尼系数无关.
4.2 双机并联离网运行仿真
VSG双机并联离网运行仿真负荷模型如图9所示.
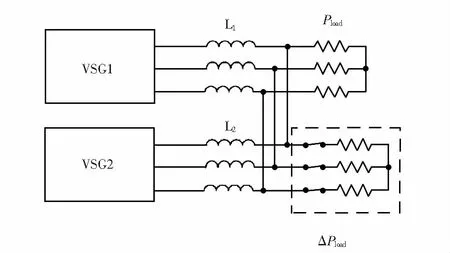
图9 VSG双机并联运行仿真模型Fig.9 Double VSGs parallel simulating model
两台VSG都采用模型Ⅰ,并采用表1中的参数,VSG1的KD分别采用表1中的3个值,仿真结果如图10所示.
两台VSG都采用模型Ⅱ及表1中的参数,VSG1的KD分别采用表1中的3个值,仿真结果如图11所示.
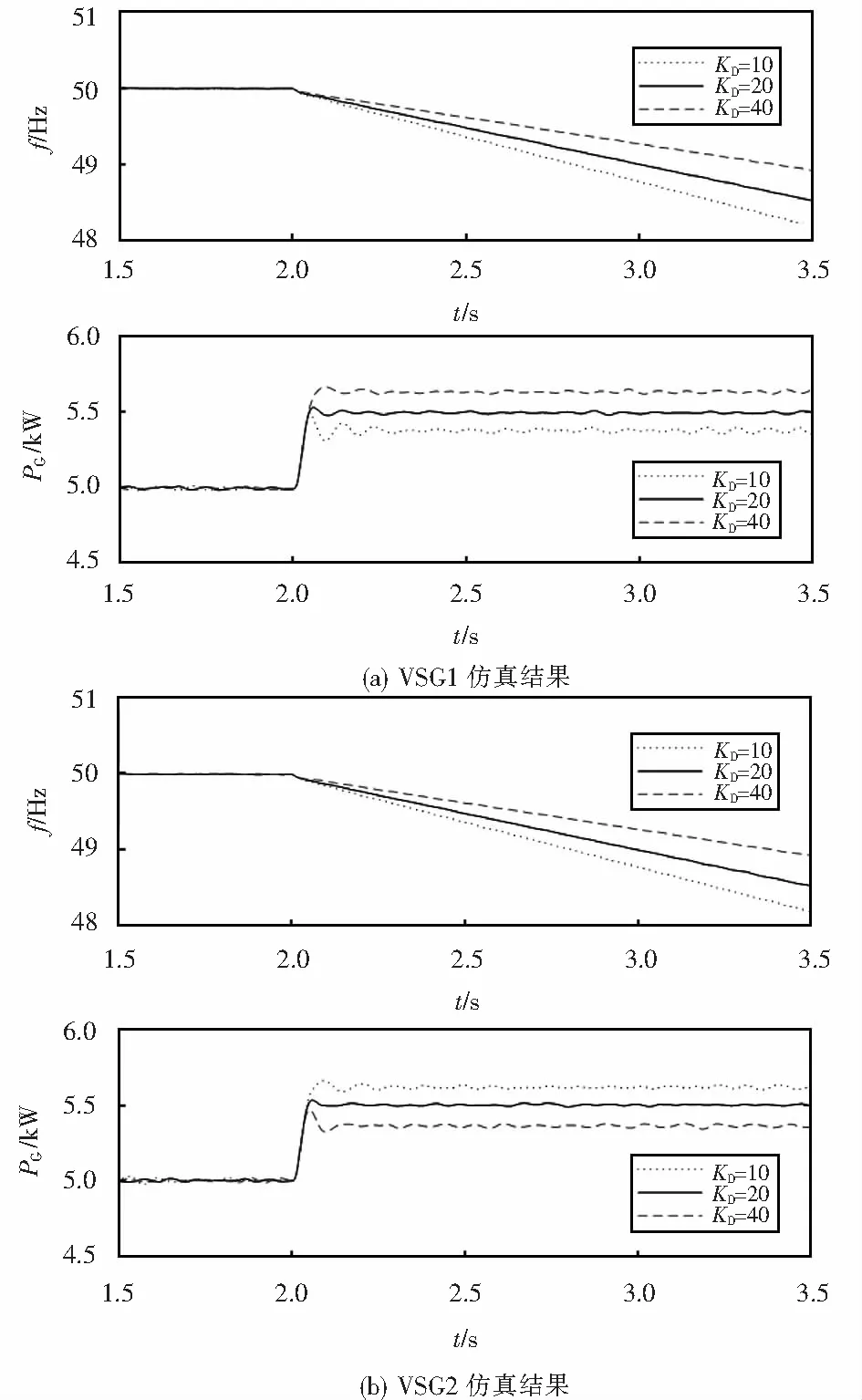
图11 控制模型Ⅱ并联时改变VSG1 KD的仿真结果Fig.11 Simulating results of double VSG control model Ⅱ with different KD of VSG1
两台VSG都采用模型Ⅲ时,选Kp=2 000π W/Hz,采用表1中VSG1参数KD的3个值,可得仿真结果图12;选KD=20 W·s,采用表1中VSG1参数Kp的3个值,可得仿真结果图13.
由图10可见:阻尼系数越大,功率扰动后,本机承担的功率变化越大,频率变化越小,这也是因为对于模型Ⅰ,仿真结果与式(5)、(6)和(12)相符,阻尼系数越大,VSG的下垂系数越大,频率变化越小,对功率扰动贡献越大.从图11可以看出:VSG的输出频率呈近似直线下降,无法保持频率稳定,但阻尼系数KD越大,频率下降的速度越慢,这是因为对于模型Ⅱ,仿真结果与式(16)相符,VSG下垂系数等于0,与阻尼系数无关,阻尼系数只是影响过渡过程,阻尼系数越大,过渡过程越慢.从图12和13可以看出:模型Ⅲ的阻尼系数只影响动态过程,不影响下垂特性,其下垂特性由下垂系数决定,仿真结果与式(18)相符.
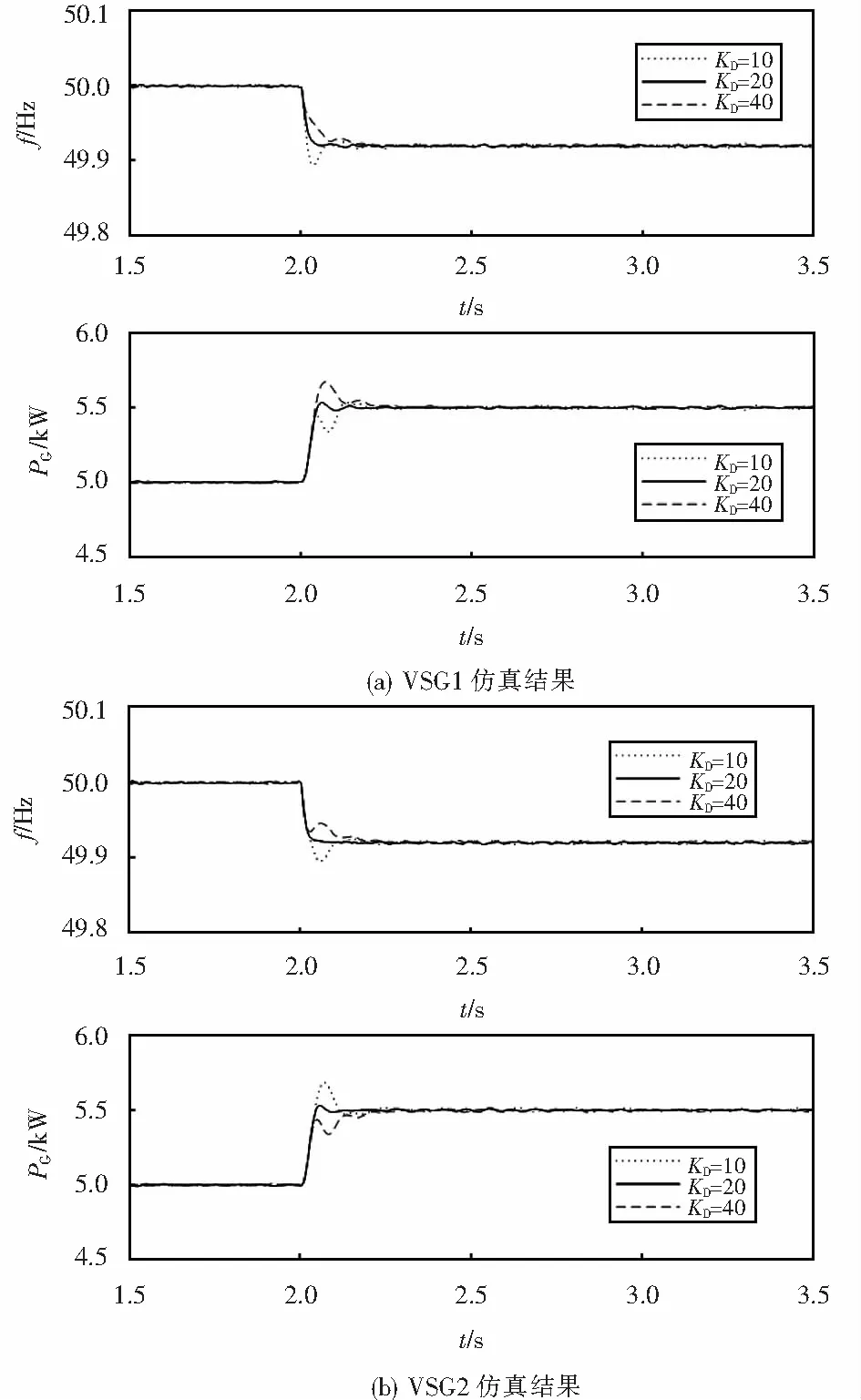
图12 控制模型Ⅲ并联时改变VSG1 KD的仿真结果Fig.12 Simulating results of double VSG control model Ⅲ with different KD of VSG1
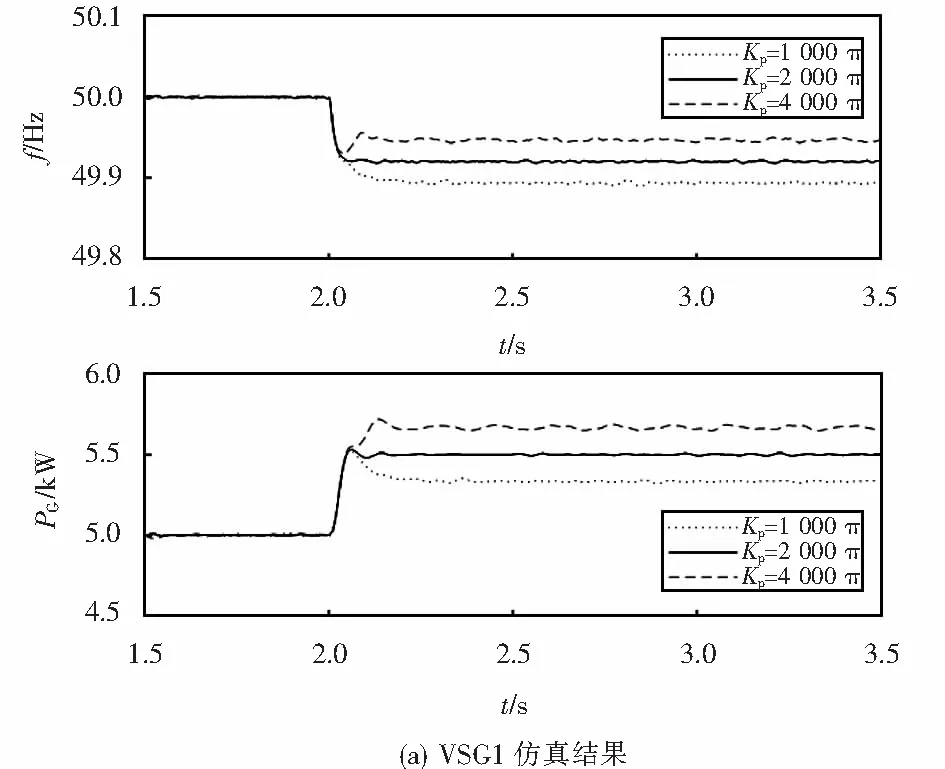
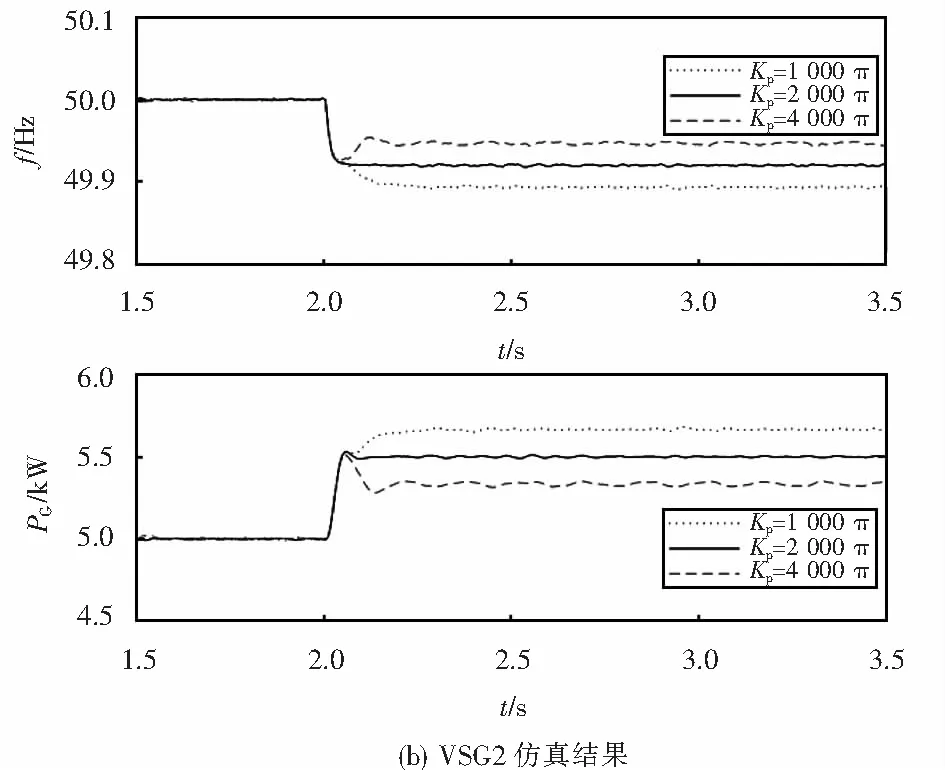
图13 控制模型Ⅲ并联时改变VSG1 Kp的仿真结果Fig.13 Simulating results of double VSG control model Ⅲ with different Kp of VSG1
5 结论
针对不同阻尼项的VSG模型,本文在分析下垂特性的基础上,建立了三种VSG仿真模型.通过两种运行场景的仿真验证,可得出以下结论:
1) 模型Ⅰ具有下垂特性,其下垂系数由阻尼系数决定.该模型具有频率自动调节和功率分配能力,所以采用该模型设置阻尼系数时不仅考虑其振荡特性,还要考虑其所对应的下垂特性.该模型适合于单机或微电网场景.
2) 模型Ⅱ不具有下垂特性,不具有频率调节能力,但具有恒定功率输出能力.离网运行时,功率扰动后无法维持频率稳定,可应用于并网但不需参与频率调节的机组.该模型可以用于尽可能提高本机能量利用率占比较小的新能源发电场景.
3) 模型Ⅲ具有下垂特性,但其下垂系数与阻尼系数无关,而是由设置的下垂系数决定,因此具有一定的灵活性.
