一种适用于大气污染数据聚类的距离度量
2022-04-26张忠帅杨鹏飞
张忠帅,陈 梅,杨鹏飞
(兰州交通大学 电子与信息工程学院,兰州 730070)
近些年,由于人口的不断增长和生产技术的持续发展,环境污染日益严重,空气质量不断下降,严重影响了公众健康.为此,研究者在大气污染源识别、污染物的远程传输途径以及制定和实施有效的控制和缓解策略等方面开展了大量的研究工作.空气污染数据测量值并不是一个值或者具有单一的属性,而是由不同类型的污染物元素组成的,所以采集的污染物数据集通常是多维数据集,同时包含了大量的异常值,因此,在对污染物溯源分析、传播路径研究时,需要综合考虑这些因素,而污染物数据的多维性、空间的复杂分布、异常点的干扰等影响了这些研究的结果准确性[1].聚类分析按照数据点间的相似性进行分类,使得相似的数据点自然地被划分到同一个簇,不相似的数据点被划分到不同簇.聚类分析有利于更准确地分析区域间的污染特征,揭示不同地区间污染的相似性与关联性,明晰污染特征[2].
作为数据挖掘中的一种重要技术,聚类是大气污染分析中一个强有力的工具[3],常用的算法有k-Means[4-5],k-Medoids[6]以及DBSCAN(density-based spatial clustering of applications with noise)[7]等.文献[8]使用SOM(self organizing maps)和k-Means分析了气象条件与几种空气污染物之间的关系;文献[9]使用k-Means算法分析了不同空气污染排放源特征;文献[10]在空气污染监测网络中,使用一种基于k-Medoids算法的分区方法来检测信息冗余;文献[11]采用分布式实现的k-Means对不同位置空气污染模式进行了研究;文献[12]利用DBSCAN算法和Convex-Hull技术,构建了一种新的技术来预测未来几天的天气,该预测方法旨在减轻空气污染对人们生活的影响;文献[13]对大气污染的空气输送轨迹进行聚类分析模拟研究,给污染物来源和输送途径的研究提供新方法,进一步为大气污染防控和污染监测站点的合理配置提供科学依据;文献[14]使用SOM算法,在给定的区域发现健康和不健康地区,并揭示了空气污染模式,有助于及时采取必要的预防措施,进一步控制污染.
在聚类算法中,根据数据特征选择合适的相似性方法对获得精确的聚类结果至关重要.常见的相似性计算方法有欧氏距离、曼哈顿距离和余弦相似度等,但是这些传统相似性度量方法具有一定的局限性,比如应用最广泛的欧氏距离,并不适用于维数较大的数据.而大气污染数据通常由多个污染元素组成,从而属性较多,每个数据点具有较高的维数,对这种情况通常的处理方式是对高维度数据集进行降维处理.但对于大气污染抽样数据集,进行降维处理会丢失污染信息,使一些污染元素特征模糊,导致聚类结果不准确.而且大气污染抽样数据集中同一个数据点的不同元素间的数量级差别通常非常大,比如,在同一时刻元素Si的浓度为15.211 μg/m3,元素As的浓度为0.002 μg/m3,在这种情况下,如果使用常用的欧氏距离,元素As假如有很明显的相对浓度变化,即它携带了很明显的污染特征,但由于元素Si、As的浓度之间的数量级相差悬殊,即使Si的相对浓度稍有变化,它对欧氏距离的贡献也会远大于As.这时,最常用的手段是对数据进行标准化处理,但标准化处理不可避免地会造成数据污染特征损失.为了提高对大气污染物数据聚类的准确性,本文根据大气污染物数据的特点,提出了一种新的距离度量方法.在该方法中,首先分别获得两点在每一维下的两个值,求得这两个值的较大值和较小值的差值与较大值的比值;然后将两点在所有维度下的比值的最大值定义为这两点间的距离.如果两个点的大气污染抽样数据距离(air pollution data distance,简称PD距离)小意味着两点污染程度处于同一水平,否则表示两个点之间某种污染物的浓度急剧变化,即发生了某种元素的严重污染.
1 相似性度量方法
1.1 传统相似性度量方法
常用的度量数据点之间相似性的函数包括三个距离函数和两个相似性函数.首先,将大气污染采样数据集表示如下:
Dp={x1,x2,…,xn},
(1)
其中:n为数据集D中数据点的数量;p为每个数据点的属性数量.
对于数据集中任意两个点xi(1≤i≤n)∈Dp,xj(1≤j≤n)∈Dp,
xi={xi1,xi2,…,xip},
(2)
xj={xj1,xj2,…,xjp}.
(3)
其中:xi(1≤i≤n)∈Dp是p维上第i个数据点;xj(1≤j≤n)∈Dp是p维上第j个数据点;xik(1≤i≤n,1≤k≤p)∈Dp是一个非负的数值,表示点i在第k维的属性值.
常用的距离函数和相似性函数有:
1) 欧氏距离(Euclidean metric,简写为EUC).欧氏距离是常见的距离计算方式,用于各种聚类算法,它用来计算两点之间的最短距离,其表达式为
(4)
2) 曼哈顿(或城市街区)距离(Manhattan distance,简写为MH).计算的距离是两点之间对应分量的差值之和,其表达式为
(5)
3) 切比雪夫距离(Chebyshev distance,简写为CB).它取两点任意一维之间的最大距离值,其表达式为
(6)
4) 余弦相似性(Cosine similarity,简写为CON).余弦相似性是内积空间中两个向量之间相似性的度量,度量的是它们夹角的余弦值,其表达式为
(7)
5) 皮尔逊相关系数(Pearson correlation coefficient,简写为PEAR).该函数是用于度量两个向量xi和xj之间的相关性,其表达式为
(8)
1.2 PD距离度量
1.2.1 大气污染抽样数据特点
在对特定领域的数据进行聚类分析时,为得到更好的结果,需要分析样本数据的特征以及基本性质.对于大气污染抽样数据,有以下特性:
1) 大气污染抽样数据点都包含同样的污染特征或属性,每个属性的类型通常都是数值型的.这些属性都是污染物排放量的一个组成部分,因此两个大气污染物的数据点是否相似取决于这两个数据点的每一维属性.当且仅当所有属性都相似时,两个污染物数据点才是相似的.
2) 大气污染抽样数据通常包含了很多种污染元素浓度或污染指标情况,数据属性较多,因此每个数据点的维数都较高.
3) 由于大气中颗粒物浓度差异较大,尤其在遭遇极端天气情况下,大气污染抽样数据集中不同元素的污染物浓度有时会相差好几个数量级.
1.2.2 PD距离
本节将详细描述适用于大气污染数据聚类的PD距离度量.
定义1对于Dp中的两个点xi和xj,xik,xjk分别为点xi和xj在第k维的值.定义higher()函数,若xik≥xjk,则higher(xik,xjk)=xik;若xik 定义2对于Dp中的两个点xi和xj,xik,xjk分别为点xi和xj在第k维的值.定义lower()函数,若xik≤xjk,则lower(xik,xjk)=xik;若xik>xjk,则lower(xik,xjk)=xjk. 对于每一维度,设xi,xj∈Dp,则 (9) 其中:higher(xik,xjk)=xik为xik,xjk中较大值;lower(xik,xjk)=xik为xik,xjk中较小值. 同时,考虑到较强的空气污染可以导致数据某一维的数据值急剧增大,而急剧增大的数据正好可以反应出当前污染特征.比如:硝酸根和硫酸根离子的浓度急剧增大意味着酸雨污染.由此,本文定义xi和xj间的PD距离如下: (10) PD距离满足以下性质: 1) 反应了污染物浓度变化特征.使用PD距离度量不用对数据集进行降维或标准化处理,保留了数据集的全部信息,在式(9)中,通过higher(xik,xjk)-lower(xik,xjk),刻画了大气污染数据集中第k维上某污染元素浓度的变化,可以很好地反应出数据集中污染浓度变化特征. 2) 对称点之间距离相等,即PD(xi,xj)=PD(xj,xi).对于一对点xi,xj∈Dp,xi到xj的距离等于xj到xi的距离. 3) 消除了维数的影响.如式(9)所示,PD距离的大小取决于一对点(xi,xj)在相同维度下,较大值与较小值的差与较大值的比值.从式(9)中可以看出,两点之间PD距离的大小与其它维度无关,因此,它可以消除数据的维数对聚类结果的影响. 4) 消除数量级的影响.在大气污染抽样数据集中,不同污染物浓度的数量级可能差别很大.比如:某日某地区沙尘暴天气,空气质量指数中PM10的指数远高于其他污染指数,各指数间数量级相差很大.如果使用常见的距离度量,其他污染物指数的变化就会被掩盖;而在PD距离中,通过higher(xik,xjk)-lower(xik,xjk)与higher(xik,xjk)作商,可以消除不同污染物浓度值之间数量级的影响,从而降低大气污染抽样数据集中每一维上数据数量级不同对聚类结果的影响.因此,PD距离度量适用于大气污染抽样数据集聚类分析中的距离计算. 通过在4个经典聚类算法及两个新聚类算法中切换不同的相似性函数,对比分析PD距离与其它几个距离及相似度在同一数据集上的聚类性能.使用的数据集包括人工合成大气污染受体数据集、真实大气污染受体数据集和兰州市空气污染指数数据集. 2.1.1 对比算法分析 为了评估PD距离的实际性能,对比实验使用了6种聚类算法,也是大气污染物分析中较为常见的聚类方法.其中:k-Means,k-Medoids,DBSCAN,OPTICS[15]4个算法是非常经典的聚类算法;MulSim[16]和AnyDBC[17]是近几年提出的新算法,由相应作者提供代码.下面对6个对比算法进行简单分析. k-Means和k-Medoids这两个算法是基于划分的经典算法,k-Medoids算法实质上是对k-Means算法的优化和改进.二者都是先随机选取中心点,然后将剩余点划分到离它最近中心点所在的簇;更新簇中心,重复这一过程,直到中心点不再变化.二者的区别是更新簇中心的方式,k-Means更新的簇中心是簇中所有点的平均值,k-Medoids挑选的簇中心是实际样本点.这两个算法中,初始中心点的选取对结果影响较大. DBSCAN和OPTICS这两个优秀的算法是基于密度的聚类算法.DBSCAN的特性是将出现在特征空间密集区域的“核心点”与被分类为不属于任何簇的离群值(“噪声点”)分开.它可以识别具有任意形状的簇,但如果数据集密度不均匀时,得到的结果较差,且结果受参数影响较大.OPTICS算法可以看作DBSCAN的改进算法,在聚类过程中,首先创建一个存放核心点与其核心距离按可达距离升序排列的所有邻居点的队列和一个存放按处理先后顺序输出的数据点的队列;然后,迭代地搜索核心点及其直接可达点,将可达距离最小的点放到结果序列中,直到所有数据点都被标记;最后生成一个以数据点输出次序为横轴,可达距离为纵轴的增广的簇排序.OPTICS算法可以获得任意密度下的结果. MulSim和AnyDBC是近几年提出的新算法.MulSim定义了一种新的策略,即当且仅当一个点与另一个点相似,且同时与这个点一个或多个最近邻相似,则将这两个点划分在同一簇.这种策略可以发现数据集中任意密度、任意形状、任意大小的簇.AnyDBC算法的核心是一种主动学习的方法,与经典算法相比,AnyDBC不是对所有的数据点进行搜索查找,而是学习当前数据集的簇结构,选择一些最理想的对象来进行范围查询.因此AnyDBC与DBSCAN相比,它最终执行的查询范围要少得多.此外,AnyDBC基于初始簇进行划分,以减少搜索时间.对于数据量非常大和复杂的数据集,AnyDBC有着出色的表现. 2.1.2 评价指标分析 本文使用的算法评价指标有三个:两个外部评价方法和一个内部评价方法. 当数据集中簇的真实结构已知时,使用外部评价方法ARI(adjusted rand index)[18]和NMI(normalized mutual information)[19],ARI取值范围是[-1,1],NMI取值范围是[0,1],这两个指标的值越大表示聚类结果与真实结果越接近;当数据集中簇的真实结构未知时,使用内部评价方法DBI(davies-bouldin index),DBI也称为戴维森堡丁指数,它的值越小,代表簇内越紧密、簇间越离散,意味着聚类效果越好. 2.1.3 参数分析 图1、表1和表2分别展示了PD距离与对比的相似性函数分别在3个数据集和6个对比算法下的实验结果,表中包含了最优聚类结果下的评价指标以及相应的参数值.其中:k-Means,k-Medoids的参数k为簇的个数;DBSCAN的两个参数ε和MinPts分别为每个点的最小邻域半径以及半径内最小点的个数;OPTICS中k为最近邻的个数;MulSim中两个参数为距离阈值k和两点中某一点的邻居数m;AnyDBC有两个参数,分别是最小邻域半径r以及半径内最小点的个数m. 图1 在人工合成的大气污染抽样数据集上的聚类结果Fig.1 Clustering results on the synthetic air pollution datasets 表1 在真实空气污染采样数据集上的聚类结果 对于k-Means与k-Medoids算法,当数据集簇数已知时,使用ARI和NMI评价指标,迭代地调整算法各自相应的参数,得到最大的ARI和NMI,确定最优的聚类结果.当数据集簇数k未知时,使用DBI评价指标,迭代地调整算法中各自相应的参数,得到最小的DBI,确定最优的聚类结果. 对于算法DBSCAN,OPTICS,MulSim和AnyDBC,其最优结果都通过对相应的外部评价指标和内部评价指标迭代寻优获得. 2.2.1 数据集介绍 本实验评估从具有不同特征的人工合成的大气污染抽样数据集所得到的聚类结果,数据集来自文献[20].该数据集形成过程为:每次从8个标准污染源中随机选择两个,改变它们的质量浓度,得到新的源贡献的中心点;然后根据标准源成分谱,生成800个受体数据点并标记为簇1;接下来重复3次该过程,再生成3组各包含800个受体数据点,并分别标记为簇2、簇3和簇4;最后将4组数据点随机打乱顺序,加入到同一个数据集中,形成共有3 200个带标签的数据点的数据集. 2.2.2 结果分析 如图1所示,图中展示了PD距离与其他对比相似性函数在人工合成的大气污染抽样数据集中6个对比算法下的聚类评价结果,其中包括最优结果的ARI和NMI值.对于每个算法,通过设置相应的输入参数迭代进行,其最优的聚类结果都由最大的ARI和NMI确定.由于已知数据集共有4个簇,因此k-Means和k-Medoids中参数k的值设为4.图1中OPTICS算法在余弦距离和皮尔逊相关系数中存在无效值,AnyDBC算法在切比雪夫距离中存在无效值,这是因为这两种算法都是基于密度的聚类算法,由于数据集的特殊性,在调整参数对ARI和NMI迭代寻优的过程中,始终无法得到有效的密度,导致每一个数据点被划分为一个单独的簇,产生了无效的聚类结果. 1) 在k-Means和k-Medoids算法中,使用PD距离的聚类结果最好,ARI和NMI值都为1.000,可以准确地识别出数据集中的真实簇结构,优于其他距离函数下的聚类结果;采用余弦相似度和皮尔逊相关系数的结果分别获得了第二位和第三位的名次;使用切比雪夫距离和欧氏距离的结果值紧随其后;在这两个算法中,使用曼哈顿距离下的聚类结果最差. 2) 在DBSCAN和OPTICS算法中,PD距离下的聚类结果与其他距离及相似度下的聚类结果相比仍为最优.在DBSCAN算法中,使用PD距离得到的ARI和NMI结果值均为1.000;切比雪夫距离和欧氏距离下的结果值排名第二和第三;曼哈顿距离下的聚类结果相较之下为最差.在OPTICS算法中,使用PD距离的聚类结果与切比雪夫距离下的结果一样,同为最优;其后分别是曼哈顿和欧氏距离下的结果值. 3) 在MulSim和AnyDBC两个算法中,PD距离下的ARI和NMI值均为1.000.在MulSim算法中,欧氏距离和切比雪夫距离下的结果与PD距离下的结果同为最优;曼哈顿距离和皮尔逊相关系数下的结果分别排第二位和第三位.AnyDBC算法中,PD距离下的结果最优;欧氏距离和切比雪夫距离下的结果值也较好,但次于PD距离.对于曼哈顿距离,通过大量实验调整参数,聚类结果始终为一个簇,结果值无效. 根据以上分析可得:在该数据集上,6个聚类算法使用PD距离的聚类结果均为最优,而其他距离函数在不同的算法中表现不一致. 2.3.1 数据集介绍 2.3.2 结果分析 如表1所列,表中展示了PD距离与其它对比相似度函数在空气污染真实采样数据集中6个对比算法下的聚类评价结果.由于数据集为实际采样中得到,真实簇结构未知,因此使用内部评价指标DBI.DBI的值越小,聚类效果越好.所以对于每个算法,通过设置相应的输入参数迭代进行,其最优的聚类结果都由最小的DBI确定.在k-Means和k-Medoids算法中,参数的值是评价指标值最好时所对应的参数.观察表1中数据可得: 1) 在k-Means算法和k-Medoids算法中,最好的聚类结果是在使用PD距离时获得.在k-Means算法中,仅次于最优值的分别是曼哈顿距离和皮尔逊相关系数下的结果值,欧氏距离则在该算法中表现不佳;在k-Medoids算法中,排名第二位和第三位的分别是在余弦相似度和皮尔逊相关系数下的取值. 2) 在DBSCAN算法中,聚类效果最好的是使用PD距离下的结果,排名第二位的是使用切比雪夫距离下的结果,使用曼哈顿距离下的结果和使用欧氏距离下的结果很接近,分别排第三、第四名,效果最差的是使用余弦相似度下的结果;在OPTICS算法中,DBI值最小的是使用PD距离函数的结果,其次分别是使用曼哈顿距离和欧氏距离的结果,使用余弦相似度下的结果最差. 综合所有结果可知:在真实空气污染采样数据集上,使用PD距离函数在绝大多数算法中均能取得较优的聚类结果. 2.4.1 数据集介绍 本实验使用兰州市空气质量指数数据集来评估PD距离的性能,空气质量指数数据由兰州气象局提供.数据集包含了2001-2011年的兰州空气质量指数,每天一个数据,共4 018个数据点,包含了SO2、NO2和PM10三种空气污染物浓度. 2.4.2 结果分析 如表2所列,表中展示了PD距离与其他对比相似度函数在兰州市空气质量指数数据集中6个对比算法下的聚类评价结果,本实验采用内部评价的方法.由于兰州市为温带大陆性气候,四季特征分明,每个季节的空气质量也相差较大,故在k-Means和k-Medoids这两个算法中将参数k设为4,然后寻找最优值.在OPTICS算法中,采用PD距离在邻居个数大于2时,算法将数据集划为一个簇,聚类结果无效;为了消除参数范围不同带来的影响,将其他距离函数下的参数也在邻居小于2的值中寻优. 1) 在k-Means和k-Medoids算法中,6个距离下的DBI值都较高,相比之下,在PD距离下的DBI值最小,聚类效果最好.其中:在k-Means算法中,采用欧氏距离和切比雪夫距离的聚类结果分别排第二和第三位,采用余弦相似度的结果最差;在k-Medoids算法中,采用曼哈顿距离和欧氏距离下的聚类结果较优,使用皮尔逊相关系数的结果最差. 表2 兰州市空气质量指数数据集上的聚类结果 2) 在DBSCAN算法中,聚类结果最优的是使用PD距离下的结果,使用切比雪夫距离和曼哈顿距离下的结果虽然不如使用PD距离下的结果,但也表现较优,最差的是使用皮尔逊相关系数下的结果.在OPTICS算法中,使用PD距离得到的DBI值最小,结果最优,其余的结果值相差不大,使用余弦相似度和皮尔逊相关系数不能产生正确的划分. 3) 在MulSim算法中,使用PD距离的结果明显优于其他距离函数下的结果.其中:使用余弦相似度的结果排名第二位,使用曼哈顿距离的结果排名第三位,使用皮尔逊相关系数的结果最差.在AnyDBC算法中,使用PD距离的结果值最优,排名第二位和第三位的结果值分别是使用曼哈顿距离函数的结果值和使用欧氏距离函数的结果值.DBI值最大的是使用余弦相似度下的结果值,聚类效果最差. 由以上分析可得:在兰州市空气质量指数数据集上,PD距离在6个聚类算法中表现仍为最优,聚类效果最好,性能优于其他传统距离函数以及相似性函数;欧氏距离函数在k-Means和k-Medoids这两个算法中表现较优;切比雪夫距离和曼哈顿距离在DBSCAN算法中表现较好;余弦相似度在MulSim算法中结果较好. 为了提高对大气污染抽样数据聚类的精确性,本文针对大气污染物数据的特点,提出了一种新的相似性度量——PD距离.PD距离用所有维度的最大值检测是否发生了某种污染,另外还可以反应大气污染物浓度变化特征,消除维数以及不同属性间数量级的差异对聚类结果的影响.为了验证PD距离的性能,在3个大气污染抽样数据集中,将PD距离与其他5个传统的距离及相似性度量方法分别在6个聚类算法中进行对比.仿真实验结果表明:使用PD距离得到的聚类结果在6个聚类算法中均优于使用其他传统距离得到的结果.在下一步的研究中,将基于PD距离提出一种基于密度的大气污染数据聚类算法,得到更优的聚类结果,并在此基础上进一步分析大气污染特征.
2 仿真实验结果分析
2.1 对比算法及评价指标和参数分析

2.2 人工合成大气污染抽样数据集实验分析
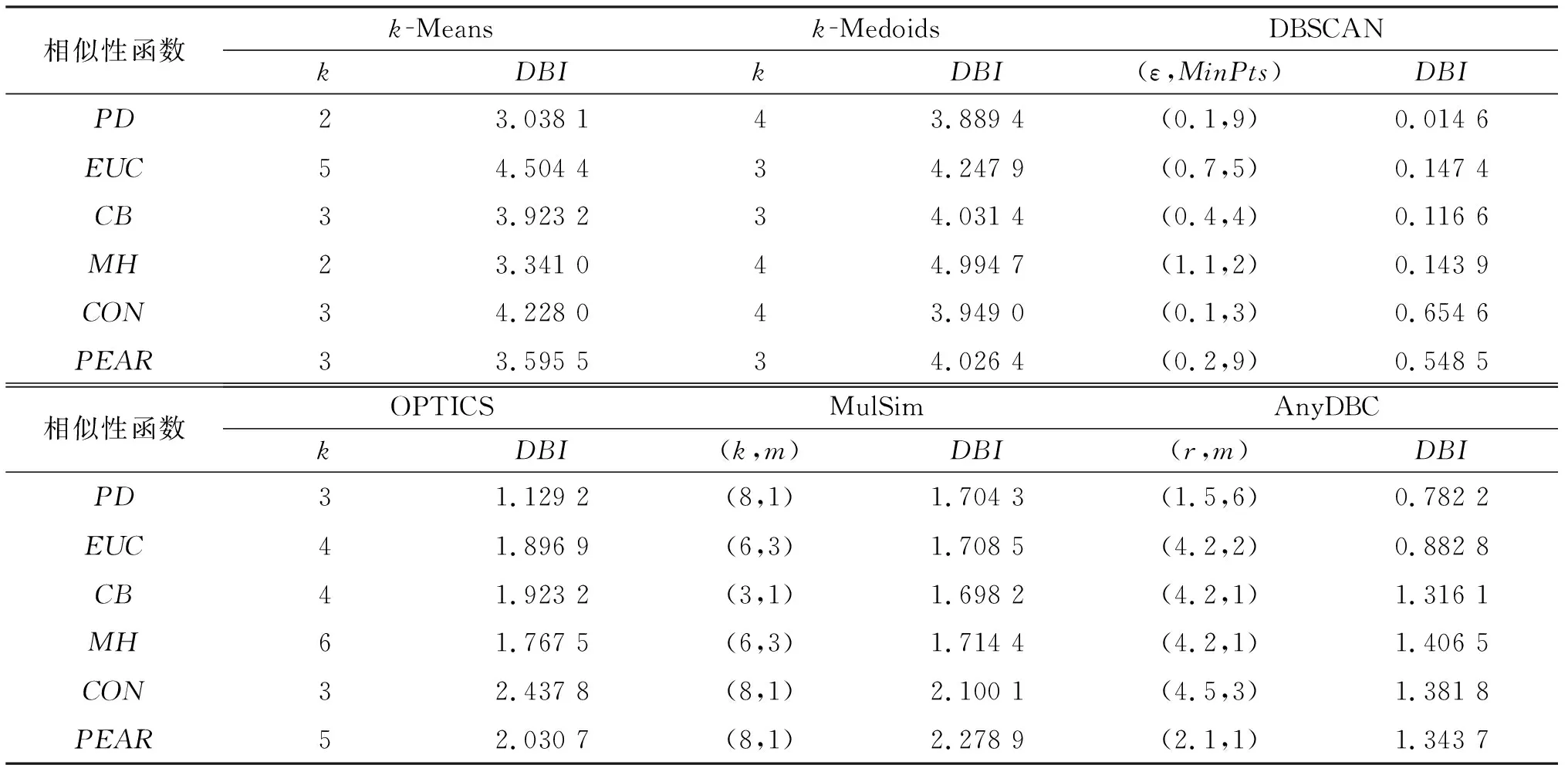
2.3 真实空气污染采样数据集实验分析

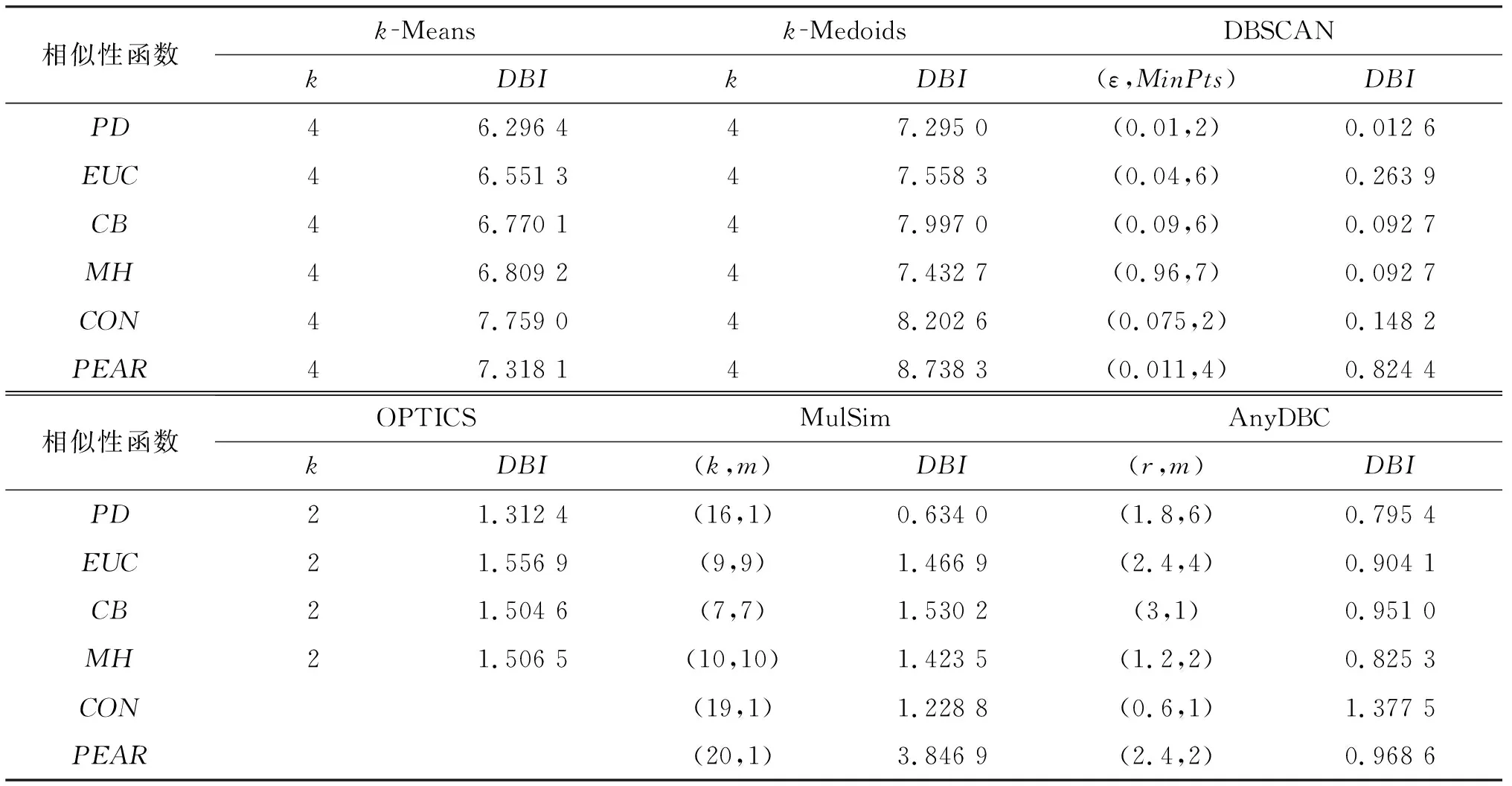
2.4 兰州市空气质量指数数据集实验分析
3 结论
