基于改进KFDA与DE优化SOM的故障诊断模型及其化工过程诊断

李国友，张新魁，才士文，贾曜宇，宁泽

（燕山大学智能控制系统与智能装备教育部工程研究中心，河北 秦皇岛 066004）

近年来，化工生产行业爆炸事故引起了各界关注，由于其原料或产物易燃易爆的特性，化工过程一旦发生爆炸事故，便会对环境造成严重的污染，而且对人身安全也会产生巨大的隐患。因此为保证化工生产过程的安全高效，构建一个针对化工过程的故障检测与诊断模型显得至关重要。随着工控技术与仪器仪表技术的不断完善与进步，采集数据设备精确度随之提高，基于数据驱动的故障诊断技术应运而生。经典的数据驱动故障检测方法有独立主元法（independent component analysis,ICA）、主成分分析（principal component analysis, PCA）、支持向量机（support vector machines, SVM）、神经网络等。但是在实际化工过程中，采集到的数据一般都具有高维度、非线性、故障类别不易区分的特征，单一的PCA、线性判别分析（linear discriminant analysis,LDA）等降维算法针对一些简单的线性特征能够很好地区分，但处理复杂的化工数据时并不能很好地提取出判别特征用于诊断模型进行故障诊断，导致故障诊断准确率下降。因此研究多算法相融合的化工过程故障检测与诊断模型显得尤为必要。

综合上述分析，本文提出了一种基于改进核Fisher 判别分析和差分进化算法优化自组织网络（KFDA-DE-SOM）的故障诊断方法。该方法首先利用欧式距离改进的KFDA算法从复杂的工业数据中提取判别特征矩阵用于后续诊断模型训练及测试，其次运用DE优化SOM网络的诊断模型对故障数据集进行训练分类，将这些高维的数据投影到二维平面，将正常工况与故障点划分为不同的区域。通过TE过程的实验数据与PX歧化单元的数据进行诊断测试，结果表明，本研究提出的方法较单一的SOM网络算法具有较好的分类诊断性能。

KFDA-DE-SOM整体算法框架如图1所示。

图1 KFDA-DE-SOM故障诊断框图

1 基于改进KFDA算法的特征提取

1.1 核Fisher判别分析

Fisher 判别分析作为一种有监督学习的数据降维和特征提取方法，在模式识别和故障诊断领域应用广泛。但在实际化工过程中，Fisher判别分析算法针对高维度、非线性的数据分析存在一定局限性，因此引入核函数相关理论进行优化，以解决上述问题。

式中，m为第类数据样本映射后的均值；为总的数据样本均值,计算方法分别如式(3)、式(4)所示。

在 特 征 空 间中，Fisher 判 别 准 则 为()，如式(5)。

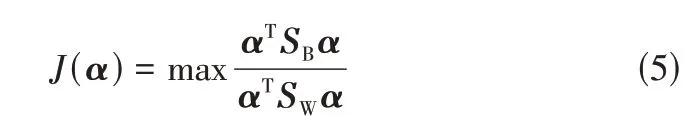
式中，为任意非零列向量；KFDA 算法利用判别准则函数()求得最优的判别矢量。

根据判别准则()求判别矢量等价于求广义特征方程，如式(6)所示。

针对可能存在奇异矩阵的问题，可以采用奇异值分解的方法来处理，对奇异值分解如式(7)所示。

依据式(9)求得最优核判别向量。

1.2 改进核Fisher判别分析

在实际情况中，由于数据类别间的距离差异过大会导致分类结果不准确，为解决上述问题，采用欧氏距离对类间离散度进行加权，调整权重，优化分类性能。改进后的类间离散度如式(10)。

式中，m和m分别表示类别和类别的均值；d代表类别和类别间的距离；W(d)为权重函数；

1.3 改进核Fisher判别分析特征提取具体步骤

步骤1：选定恰当的核函数，将原始故障数据利用核函数映射到高维空间得到新的数据矩阵。

步骤4：根据求解得到特征向量确定的判别矩阵=[,,···,α]。

步骤5：依据核处理后的数据矩阵与判别矩阵求出新的训练矩阵，计算方法如式(12)。

2 DE-SOM故障诊断模型

2.1 DE算法

DE 算法是基于实数编码的全局优化算法，在寻优计算过程中能够跳出局部最优值。它的基本原理为种群内的个体经过变异、交叉、选择操作，迭代更新重组，实现种群的进化，引导搜索结果朝全局最优解靠近。

该算法主要训练步骤如下。

步骤1：种群初始化

初始化种群规模为个个体，缩放因子和交叉概率因子CR。

步骤2：变异操作

变异是差分进化算法的核心思想，主要是在父代中选定的两个个体，并对两个个体采取差分操作，将差分操作形成的差分矢量加权，并求解与其他父代个体的矢量和，公式如式(13)。

步骤3：交叉操作

交叉操作将种群的多样性增加，选取目标个体与变异个体交叉操作，生成新的个体。新个体的维度分量公式如式(14)。

式中，CR的范围为[0,1]；rnbr() ∈[1,2,…,]；rand()随机生成[0,1]范围内的实数。

步骤4：选择操作

该操作主要是根据适应度函数计算个体的适应度值，通过适应度值的比较选定较优的个体作为下一代，计算方法如式(15)所示。

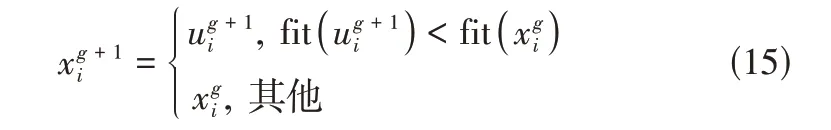
2.2 SOM算法

SOM 作为一种无监督学习的竞争神经网络，有很强的自学习能力和良好的拓扑关系保持性能，并在可视化方面拥有很大的优势，因此在模式识别分类领域应用广泛。该网络结构主要由输入层和输出层组成，输入层接受高维数据，通过竞争学习机制将高维数据变为二维数据可视化输出。

SOM训练步骤如下。

步骤1：初始化

设定学习率初值(0)、邻域半径初值(0)，神经元权值向量w。

步骤2：寻找获胜神经元

计算输入向量与输出神经元的距离d，找出获胜神经元。

式中，x为选定的向量；w为输入层的第个神经元与输出层的第个神经元的权值。距离最小的就是获胜神经元。该神经元满足式(17)。

步骤3：邻域半径内的获胜神经元权值更新，权向量的学习调整如式(18)、式(19)。

式中，表示输出层神经元；为获胜神经元；r(t)为获胜邻域。

步骤4：更新学习率和邻域半径

步骤5：判断训练次数是否达到预设值，若达到则结束训练；否则继续训练。

SOM网络算法流程图如图2所示。

图2 SOM算法流程图

2.3 DE-SOM流程

鉴于单一的SOM 神经网络在，在故障诊断识别领域的效果并不是非常理想，因此提出一种基于差分进化算法改进的SOM 网络，在很大程度上避免了产生死神经元陷入局部最优的问题，提高分类精度。

具体步骤如下。

步骤1：数据预处理

采集生产工艺原始数据，利用改进后的KFDA算法对原始故障数据进行特征提取，将得到样本特征矩阵划分为两类：测试数据集与训练数据集。

步骤2：将作为SOM 网络的输入进行训练，获得初始权值。

步骤3：用DE 算法参数寻优得到最优权值向量，将其作为SOM 网络的权值向量，搭建DESOM模型

步骤4：运用DE-SOM 网络模型对训练数据集进行训练。

步骤5：输出训练数据集故障分类结果。

步骤6：利用测试数据集对DE-SOM 诊断模型进行验证。

步骤7：算法结束。

DESOM算法流程图如图3所示。

图3 DE-SOM算法流程图

3 案例

为了验证上述基于KFDA 与DE 优化SOM 算法在故障诊断与识别方面的可行性，将该方法应用于TE过程与PX歧化工艺流程。

3.1 TE过程

TE 过程是一个典型的化工过程，主要包括反应器、冷凝器、气液分离器、汽提塔、循环压缩机5 个操作单元，流程如图4 所示。该过程包括53个变量，其中41 个测量变量、12 个操作变量，故障数据集是由21类预设故障和正常工况仿真而得。数据集中的测试样本集包括正常工况样本960 个，每类故障点包括160个正常样本和800个故障样本。

图4 TE化工过程工艺流程图

本案例中选取两种属性的故障（表1），故障点1、故障点2 和故障点6 是原材料的供给发生变化，故障点4和故障点5是温度发生变化，故障点14 属于阀门位置发生黏滞型故障，每个故障点采取的样本为[361,960]共600 个，构成3600×52 的故障数据矩阵。

表1 过程故障点

3.1.1 单一SOM算法

将选定的六类故障点数据组成一个3600×52矩阵，利用改进的KFDA 算法对矩阵进行特征提取得到新的特征矩阵，然后将提取到的特征矩阵输入到DE-SOM 网络中进行训练，最后输出诊断结果如图5所示。

图5 基于SOM算法对故障点1、2、4、5、6、14数据的映射

根据图5(a)可以看出，整块区域被分割成五部分，其中亮的部分代表不同故障数据的分割线。图5(b)为映射标签图，图中网格内的符号代表每类故障点在该区域所映射的次数，例如F6(23)表示故障点6 即A 进料损失在该网格中映射的数据数量为23。结合图5(a)、(b)可以看出，六类故障点被分成五个区域，并不能将六个故障有效地区分开，其中故障点4和故障点5分布的区域重叠，故障点14分布的区域与故障点4、故障点5 分布的区域边界部分不是特别明显。图5(c)为单一SOM 网络对TE 数据的测试效果图，由图中可以看出故障点4和故障点5 的测试数据并不能很好地映射在对应区域内。因此对于单一的SOM 算法在故障诊断中的精度还不能够满足化工安全生产需要，还需要对SOM 算法进行改进。

3.1.2 KFDA-DE-SOM组合算法

由于KFDA算法能够将不同种类数据之间的距离增大，因此用该算法对故障数据集进行特征提取，增大不同类别故障点间的距离，以便获得更好的分类效果。其次SOM 算法本身的框架在训练过程中易产生“死神经元”陷入局部最优，利用DE算法对该网络的权值动态的调整在很大程度上避免了这个问题。

利用改进后的KFDA-DE-SOM 算法对数据集训练，训练后的结果如图6所示，故障点1、故障点2、故障点4、故障点5、故障点6和故障点14 可以很好地区分开。与图5(a)相比，图6(a)的矩阵图边界线的区分程度大大增加，能够清晰地分辨出每类故障点所属的区域。图6(c)为测试效果图，测试数据都分布在对应的区域内，同时根据表2算法的诊断精确度验证了该算法在故障诊断方面的有效性。

图6 基于KFADA-DE-SOM算法对故障点1、2、4、5、6、14数据的映射

表2 不同算法的故障诊断精确度 单位：%

3.2 PX歧化工艺单元

PX 生产过程中，歧化反应过程属于高危单元，单元中参与反应的化学物质多为有毒的危险性物质，且在高温高压条件下易发生爆炸，因此对PX歧化单元的故障诊断至关重要。图7为PX生产过程的歧化单元工艺流程图，该工艺主要是以来自抽提装置和吸附分离装置的甲苯和芳烃分馏装置的C芳烃以及压缩机升压后的氢气为原料，混合后经换热器、加热炉等装置反应后，最后进入歧化反应器反应。反应产品部分返回到原循环系统，部分进入下一阶段反应单元。

图7 PX歧化单元

PX 歧化单元工艺常见的故障为歧化反应进料变化、汽提塔气体流速过快、氢气补充量不足、歧化反应压力变化以及加热炉温度过高五种，如表3所示。

表3 过程故障点

3.2.1 单一SOM算法

将PX 歧化单元中选定的5 个故障点数据组成一个矩阵，利用单一的SOM 网络对其进行训练，训练映射效果如图8 所示。根据图8(a)、(b)可以看出整个区域被分割为4部分，其中故障点4和故障点5分布的区域有重合的部分，在图中不能够清晰地辨别两故障。图8(c)为PX 测试集的映射效果图，从图中可以看出故障点4和故障点5并不能很好地区分开。因此单一的SOM 网络分类效果并不是很理想。

图8 基于SOM算法对故障点1、2、3、4、5数据的映射

3.2.2 KFDA-DE-SOM组合算法

首先将PX 歧化单元选定的五种故障数据组成的矩阵经改进后的KFDA 算法进行特征提取，得到新的数据矩阵，其次将数据矩阵输入到DE-SOM网络进行训练。

训练映射结果如图9 所示，从图9(a)可以看出整个区域被边界线分割成5 部分，与图8(a)相比，改进后算法映射的矩阵图故障点4 和故障点5 之间的边界线清晰度较高，通过图9(b)可以清晰地看出歧化反应进料F(1)、汽提塔气体流速过快F(2)、氢气补充量不足F(3)、歧化反应器压力变化F(4)以及加热炉温度过高F(5)五类故障所属的区域，验证了该算法对于PX歧化单元故障分类诊断的有效性。图9(c)为测试效果图，5 类故障点测试数据分布在对应的区域，表4为不同算法的诊断精度，与以往算法相比，精确度提高，说明诊断模型的有效性。

图9 基于KFDA-DE-SOM算法对故障点1、2、3、4、5数据的映射

表4 不同算法的故障诊断精确度 单位：%

4 结论

本文所提出的KFDA-DE-SOM 故障诊断方法有效结合了KFDA对高维非线性数据特征提取的能力，DE算法的优化局部极值的能力以及SOM网络聚类可视化的能力。首先利用欧氏距离对KFDA算法的类间距进行改进，改善数据投影重叠的问题，然后利用DE算法全局寻优的能力对SOM网络的权值进行动态调整优化，最后基于优化的DE-SOM网络对故障数据进行分类。运用TE过程与PX歧化反应过程的数据进行了验证，实验结果表明，本研究提出的KFDA-DE-SOM 算法相比于传统SOM 故障诊断方法，诊断精度明显提高，能够明显诊断出故障类型。

对于一些复杂的故障，本文所提出的算法诊断精度仍相对较低，在今后的研究中可以考虑与其他的故障诊断算法相融合以提高诊断精度。