变化技能在数学教学中的应用
2022-04-25常玉宝于小辉
常玉宝,牟 欣,于小辉
(1.白城师范学院 数学与统计学院,吉林 白城137000;2.白城市第四中学,吉林 白城137000)
0 引言
当前课堂教学中,仍然存在着学生的主体地位被忽视、以教师为中心、学生被动接受等现象[1].要改变这种状况,教师就要运用教学技能,促使学生主动学习.
变化技能的运用能够提高学生的学习效率,从而调动学生的学习积极性.因此,教师在课堂教学中通过转变技能方式来吸引学生的注意力,即教学方法要多种组合,教学手段要多种并用,这样才会引起学生的兴趣,能够有效激发学生的学习热情并维持学习动机,也能使学生较好地掌握知识与技能,促进学生核心素养的达成.
1 变化技能的涵义
“事物产生新的状况,初渐谓之变,变时新旧两体俱有;变尽旧体而有新体,谓之化.”这是《礼记·中庸》中对变化的解释[2].凡事变则通,通则久,课堂教学也是如此.在教学中,所谓变化是指灵活运用不同的刺激,引起学生的兴奋点,把学生的无意注意向有意注意转化,是教师教学风格形成的主要因素.
变化技能是指教师在教学过程中,通过不同的教态、教学媒体、师生相互作用方式等的变化刺激学生,高效地传递知识和交流情感,引起学生有意注意和兴趣,减轻学生的疲劳,引导学生愉快、主动地建构数学认知结构及维持良好的学习秩序的一类教学行为方式.
2 变化技能的教学意义
(1)引起注意、激发兴趣.教学过程是学生有意注意与无意注意交替运用、共同发挥作用的认知过程.课堂教学中,获得学生的注意是保证教学效率的基本条件.学生较长时间在同一种教学方式、教学氛围和教学媒体中活动过久,他们的思维兴趣、参与热情、灵感和注意程度就都会陷入低迷状态.长时间的单调刺激极易引起大脑疲劳和心理疲劳,使学生产生厌学情绪从而影响教学效果.教师运用变化技能,使教学活动和信息刺激学生而使其大脑兴奋中心转移,引起学生的惊觉反应,激发学生学习兴趣,引发无意注意,并使之转向有意注意.
(2)因材施教、构建新知.学生的数学知识基础和认知水平各不相同,教师的教学不应是一成不变的.教师应根据学生的实际情况,适时对教学内容做出调整,尽可能地照顾到每一个学生,这是因材施教的教学原则的体现,也是数学新课程理念的要求.
学生的原有认知结构各不相同,对同一数学知识的看法也不尽相同.通过变化技能的运用,教师可以调动学生从不同角度、用不同的方法认识数学知识,便于学生构建起新的认知结构.这样构建起来的认知结构才是牢固的,因为它适合学生个性化认知结构.
3 变化技能的类型
在实际课堂教学中,变化技能是多种多样的,从不同的角度可以分为不同的类型.
(1)教态变化.主要是指教师讲话的声音、手势、眼神、身体姿势的变化以及位置上的变化等.教师不仅可以运用讲授、演示、提问和练习等有形、显性的信息传递方式进行教学,还可以通过自己的语态、神态和姿态等一系列无形、隐性的信息传递方式潜移默化地达到教学目的.教态的变化是教师最基本、最常用的变化技能[3].
(2)教学媒体变化.在教学中,教师运用教科书、录音、录像、板书、板画、实物、模型和实验等媒体进行信息传递,引起学生的不同感官反应,从而实现教学信息多样化呈现.例如,某教师在椭圆及其标准方程教学设计中,就体现了这种变化.首先,丰富学生的感性认识,学生观察汽车油罐的横截面、橄榄球截面和行星运行轨迹等椭圆的图片;其次,用多媒体动画演示椭圆的形成过程;最后,学生在教师带领下,分别在画图板和黑板上用细绳和铅笔画出椭圆的图形.在经历了上述教学活动后,教师开始提问,总结椭圆形成的条件和椭圆存在的条件.这样的教学,教学媒体不断变化,兴奋点不断转换,学生参与度高,注意力持久,教学效果好.
(3)师生相互交流方式的变化.师生相互交流方式具有多种形式的.在教学中,对不同的教学内容,应选择不同的师生交流方式.以学生的参与程度可以分为五种交流模式,即教师讲授、师生谈话、学生讨论、学生活动和学生独立探究.这五种交流模式在教学过程中既可以单独使用,也可以几种模式合理组合使用,每种模式的持续时间范围可从几分钟到一节课[4].
从以上对变化类型的评述可以看到,关于变化技能的讨论主要集中在教态变化、教学媒体变化和师生交流方式变化,而对教学内容本身的研究不足.下文主要针对数学教学内容方面的变化进行探讨,以充实课堂教学变化技能的研究,为其他学科教学中变化技能的运用提供借鉴.
4 数学教学内容的变化方法
在数学教学中,教师要强调某知识点的重要性或突出问题的本质,需要多次重复讲解.如果教师只是简单的语言重复,学生容易产生懈怠与厌倦情绪.此时应尝试改变讲解内容与方式,从而给学生留下深刻的印象.
4.1 变换表达方式
4.1.1 阐释角度的变化
对同一数学内容或问题,从代数、几何和三角等不同角度讲解,加强知识间的横向联系,拓展学生的视野[5].这种变化在概念教学时运用较多,最典型的就是导数概念.导数本身是函数,而它的几何意义就是曲线上某点切线的斜率.也就是说,在进行代数式或方程、函数等代数内容教学时,教师要挖掘由其所抽象成的几何图形和几何语言,两者结合进行讲解,提升学生认识层次.
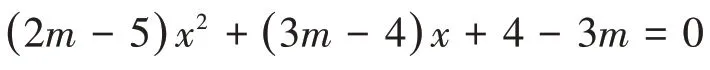
解法1:从函数与方程角度分析,一元二次方程会产生两个根,并且两根情况可由判别式的情况来判断,从而转化为解不等式的问题.
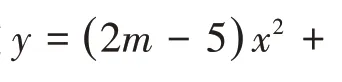
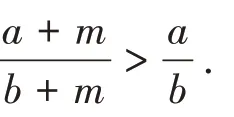
解法1:从代数角度分析,不等式的问题,可由作差法证明得到.
解法3:转化为浓度问题求解.用生活实例来印证该不等式,可表述为给咖啡加糖变甜的问题.
例3 解不等式3 < |
|2x- 3 <5.
解法1:根据绝对值的定义,进行分类讨论求解:(1)当2x- 3 ≥0 时,不等式可化为3 <2x- 3 <5,解得:3 <x<4;(2)当2x- 3 <0 时,不等式可化为-5 <2x- 3 <-3,解得:- 1 <x<0;所以,不等式的解集为{x|-1 <x<0或3 <x<4} .
4.1.2 改变非本质特征的形式变化
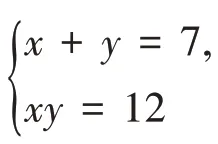
再如,在讲授函数单调性时,可以设计一些非概念变式的判断题:设f(x)是定义在R上的函数,判断:①若存在x1,x2∈R且x1<x2,使得f(x1)<f(x2)成立,则函数f(x)在R上单调递增;②若存在x1,x2∈R且x1<x2,使得f(x1)≤f(x2)成立,则函数f(x)在R上不可能单调递减;③若存在x2∈R,对于任意x1∈R,都有f(x1)≤f(x1+x2)成立,则函数f(x)在R上单调递增;④对任意x1,x2∈R且x1<x2,都有f(x1)≥f(x2)成立,则函数f(x)在R上单调递减.
通过上述变式,强调了函数单调性的x1,x2有三个特征:一是x1,x2同属于一个单调区间;二是任意性,即任意取x1,x2,“任意”二字绝不能丢掉;三是有大小,通常规定x1<x2,三者缺一不可.
4.2 变换解题方法与策略
在解题教学过程中,常常要寻求问题的多种解法,即做一题多解的训练,以开拓学生的视野.在文中已讨论过在不同知识范围内的一题多解,不再赘述.而在同一知识范围内,对已知条件的不同运用,也可以得到多种解法.

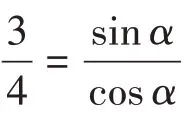

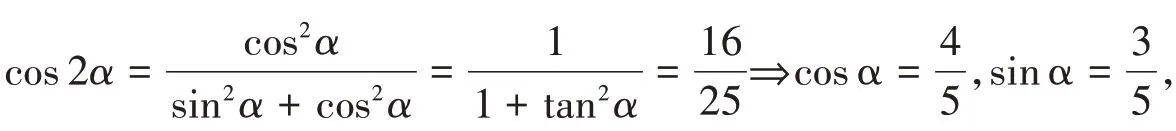
由于解题方法多种多样,不能一一列出.因此,解题教学中运用变化技能不妨采取以下策略,即陌生问题熟悉化、复杂问题简单化和抽象问题直观化.
4.2.1 陌生问题熟悉化
在解题过程中,将学生感到陌生的问题,变换为相对熟悉的或与学生已有的认知结构中的知识和经验有关联的问题来解决.
例如,解方程x3+( 1+)x- 2 = 0,这是关于变量x的三次方程,其一般解法学生可不掌握,但如果能够将其转化为学生熟悉的一元二次方程,则问题就会得到解决.因此,设y=,则原方程改写成:x3+(1+y)x2-y2= 0,即x3+x2+yx2-y2= 0,解关于y的方程得:y=-x或y=x+x2,从而将三次方程问题转化为熟悉的一元二次问题.
4.2.2 复杂问题简单化
在解题过程中把表达较复杂、繁琐的问题,通过变形、化简变更为若干相对简单的问题,然后逐个解决.
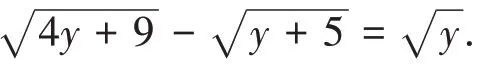
4.2.3 抽象问题直观化
在解题过程中,把比较抽象的问题找到其几何表示,以便应用数形结合的方法解题.
例如,求函数z=
5 结语
在数学课堂教学中,教师要深入研究教学内容,探究在教学中恰当运用变化技能,运用多种方式拓展知识,形成多方位的信息交流网络,丰富教学内容,增强教学趣味性,进而促进学生良好数学思维的形成.
