7075-T651铝合金铣削参数与刀具几何参数的多目标同步优化方法

陈良骥，魏子森

7075-T651铝合金铣削参数与刀具几何参数的多目标同步优化方法

陈良骥1,2，魏子森1

（1.天津工业大学 机械工程学院，天津 300387；2.桂林理工大学 机械与控制工程学院，广西 桂林 541006）

降低铣削力和铣削热，以减小7075-T651铝合金工件的加工变形，并提高金属去除率。提出一种面向2类参数（铣削参数和刀具几何参数：转速、进给量、径向切深、轴向切深、前角、后角）旨在实现多个目标（铣削力、铣削温度和金属去除率）同步优化的方法。基于偏最小二乘法回归模型和7075- T651铝合金工件铣削有限元仿真模型，建立关于2类参数的铣削力、铣削温度及金属去除率的函数关系，并采用8种典型多目标优化算法进行求解。通过Pareto前沿曲面的可视化和HV性能指标，筛选出适合解决本文问题的优化求解算法，获得的部分铣削参数，转速为5 966.30 r/min，进给量为0.08 mm/z，径向切深为4.53 mm，轴向切深为4.99 mm。刀具几何参数分别为前角17.95°、后角2.00°，此时对应的铣削力为232.12 N、铣削温度为22.56 ℃、金属去除率为33.08 mm3/min。上述优化结果可实现较低铣削力和铣削温度以及较高金属去除率等综合控制目标，对7075-T651铝合金工件铣削加工时降低工件变形量和提高加工效率等方面具有实际应用价值。

铣削参数；刀具几何参数；铣削力；铣削温度；多目标优化

在金属切削过程中，铣削参数与刀具几何参数是影响切削效果的最直接因素[1-4]。虽然目前国内外学者在对铣削参数与刀具几何参数进行优化时所使用过的算法种类较多，但是由于尚缺少同时可以针对铣削力、刀具铣削温度和金属去除率3个优化目标的最优算法，因而无法获得可达到满意切削效果的铣削参数和刀具几何参数，并且不能实现对上述3个目标进行同步优化及三维可视化[5-7]。由此可见，面向铣削力、刀具铣削温度和金属去除率多目标协同优化的铣削参数和刀具几何参数优化选取问题，已逐渐成为铣削仿真优化领域亟待解决的重要问题之一。

国内外研究学者在铣削力、刀具铣削温度和金属去除率的建模和提出优化算法等方面开展了相关研究工作。Saglam等[8]对不同切削参数和不同刀具几何形状下加工40HRC淬硬AISI 1040钢时，刀尖切削力和温度变化的测量结果与计算结果进行了比较，获得了最优加工时的刀具几何参数，这一结论同时考虑了切削力和刀具温度，也印证了刀具几何参数对切削力和切削温度有显著影响。潘永智等[9]研究了刀具几何参数和切削参数对铣削的影响，使用多元线性回归建立了预测模型，最后使用遗传算法优化刀具几何参数和切削参数，在保证较大的金属去除率情况下，获得更小的切削力。Yi等[10]针对传统多目标进化算法计算量庞大的问题，利用一个基于人脑电信号处理的大规模优化问题，对NSGA-Ⅲ算法3个交叉算子的性能进行了基准测试，证明了NSGA-Ⅲ算法的优越性。齐红等[11]针对使用传统加工技术切削后的工件无法达到精密要求的问题，从工艺流程角度出发，提出了一种基于改进粒子群算法和BP神经网络的优化算法，以实现微米木纤维的精密切削加工，其改进后的优化算法可以给出最优化的切削参数，保证了加工质量。赵荣荣[12]运用现代切削理论，建立了数控铣削加工切削参数优化的数学模型，并利用数学方法和仿真软件对加工参数进行优化，寻求铣削加工参数的最优组合。最终加工结果表明，运用人工神经网络对切削参数进行优化，能有效缩短切削加工时间，提高切削效率，验证了优化方案的正确性与可靠性。徐玲等[13]为预测刀具寿命，也引入人工神经网络技术，建立了刀具寿命预测神经网络模型，同时对切削参数进行优化选择，从而为刀具需求计划制定、刀具成本核算以及切削参数制定提供理论依据，节约了制造执行系统中的生产成本。李许庆等[14]以相对低的刀具最高温度和相对高的金属去除率为优化目标，利用NSGA-Ⅱ多目标优化算法获取了Pareto最优解集，在未考虑切削液的情况下，通过NSGA-Ⅱ优化算法能够有效地获取优选的粗铣叶片加工工艺参数组合，达到了控制刀具成本、提高加工质量和提高加工效率的目的。岳彩旭等[15]对不同前角、后角、螺旋角及刃口半径的球头铣刀铣削拼接模具的过程进行了模拟仿真，采用遗传算法优化铣刀结构，将优化后的结构参数与传统结构参数引入刀具磨损、工件表面质量的对比试验，从而验证了优化结构的有效性。Mustafa[16]研究了车削工艺参数对AISI316Ti钢表面粗糙度、刀具振动和温度的影响，通过验证试验确定了田口法的最佳参数组合，结果表明，表面粗糙度、刀具温度和振动都得到了良好的控制。Abdelnasser等[17]对Ti6Al4V合金采用聚晶金刚石（PCD）刀片进行车削（包括常规和高速切削）时的可加工性进行了试验研究，考察了进给量、切削速度和切削深度（每5个层次）及其相互作用对切削温度的影响。结果表明，无论是常规加工还是高速加工，切削温度均随切削速度的增加而升高。栗方[18]对6种多目标优化算法进行了测试，选择了4种不同性质的测试函数，安排了12组试验，为寻找最优的算法提供了一种思路。

然而，上述研究方法虽然分别开展了对铣削参数或刀具几何参数的数学建模工作，但由于多在研究每种参数各自对铣削力、刀具铣削温度和金属去除率的影响规律，忽略了这2种参数共同作用下将对切削效果产生的综合性影响规律，存在铣削力和刀具铣削温度建模不完整、不完善的不足之处。同时，在优化目标函数方面，上述研究方法多采用的是单目标优化（铣削力）或双目标优化（刀具铣削温度和金属去除率）算法，尚未综合考虑铣削力、刀具铣削温度和金属去除率之间的关联耦合性，而且在求解铣削参数或刀具几何参数时，分别使用了各自不同的优化算法，铣削力、刀具铣削温度和金属去除率3个目标不能同步获得最优化，铣削参数、刀具几何参数不能进行三维可视化选取。

针对以上问题，本文拟引入正交组合设计参数集，采用AdvantEdge软件对7075-T651铝合金工件铣削过程进行有限元仿真。通过仿真结果，分析铣削力、刀具铣削温度和金属去除率随铣削参数和刀具几何参数的影响变化规律，建立铣削参数和刀具几何参数到铣削力、刀具铣削温度、金属去除率的回归函数模型，实现以相对低的铣削力、刀具铣削温度及相对高的金属去除率为目标，使用多种典型算法（NSGA-Ⅱ、SPEA2、NSGA-Ⅲ、MOPSO、GDE3、AGE-MOEA、SRA、VAEA）对上述模型进行优化。最后通过Pareto前沿曲面的可视化分析和HV性能指标评定最优的优化算法，并获得Pareto最优解集和优选后的铣削参数组和刀具几何参数组。

1 7075-T651铝合金铣削有限元模拟

7075-T651铝合金工件铣削加工时，铣削力在不同阶段会呈现出不同的波动变化。当铣削力上升时，会使得铣削热上升，进而导致工件的热软化效应；而当铣削力下降时，铣削热也随之下降，此时金属材料又开始硬化。金属材料重复出现热软化和硬化的热力耦合交替过程。本文利用仿真软件AdvantEdge建立包括铣削参数和刀具几何参数（转速、进给量、径向切深、轴向切深、刀具前角和刀具后角）的二维综合铣削模型。根据工件在机床中的装夹实际情况，约束7075-T651材料基体（长为5 mm，宽为2 mm）底部边线的自由度，设置工件为可变形体，采用自适应网格。假定刀具为解析刚体，保留其沿水平方向运动的自由度，其速度等于铣削速度，如图1所示。

材料模型选用Johnson-Cook（J-C）本构模型，J-C本构将影响流动应力的应变硬化效应、应变率效应与温度效应。本文将3种效应用连乘的形式联系在一起，构建出可综合反映变形热力参数之间的数量关系表达式，见式（1）。

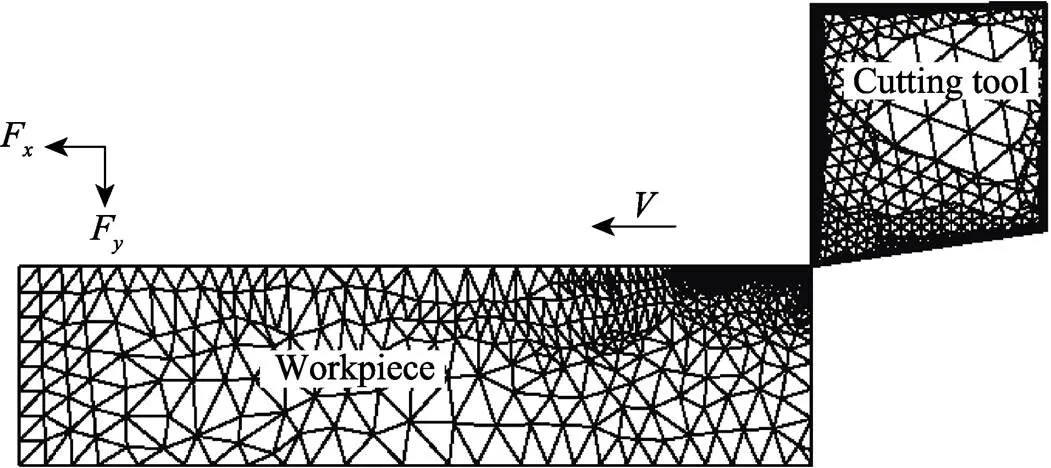
图1 二维铣削

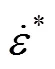
使用J-C失效准则建立切屑和工件的分离断裂失效标准，由J-C失效准则定义的单元损伤为：

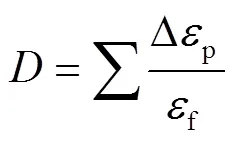
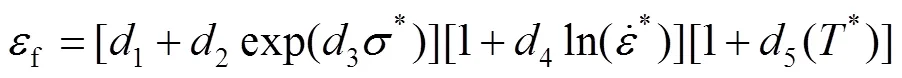
式（1）和式（2）中所需的7075-T651铝合金材料的J-C本构模型参数和J-C损伤模型参数分别见表1和表2中，后续仿真试验部分所需的7075-T651铝合金材料的力学性能参数和热力学参数见表3。

表1 7075-T651 J-C本构模型参数

Tab.1 Parameters of the 7075-T651J-C constitutive model

表2 7075-T651 J-C损伤模型参数

表3 7075-T651力学性能参数和热力学参数

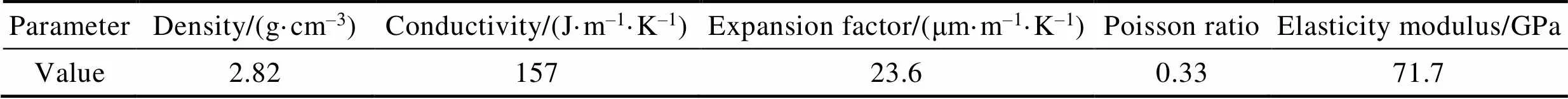
Tab.3 Mechanical property parameters and thermodynamic parameters of 7075-T651

1.1 铣削仿真正交试验

在7075-T651铝合金材料铣削过程中，转速（）、进给量（）、径向切深（e）、轴向切深（p）、刀具前角（）和刀具后角（）等铣削参数和刀具几何参数是影响铣削力和刀具铣削温度的主要因素。本文以上述6个参数为自变量，以铣削力（）和刀具铣削温度（）（刀具铣削温度采用“Peak Tool Temp”功能调用，为刀具与工件接触第一变形区的最高温度）为响应量，设计了六因素五水平正交试验，其设计参数见表4。通过仿真正交试验，获得6个参数的正交排列和仿真值，见表5。其中，F、F和分别为通过仿真获得的进给方向铣削力值、径向铣削力值和刀具铣削温度值。选取第9组参数仿真的温度场云图如图2所示。

表4 正交试验设计

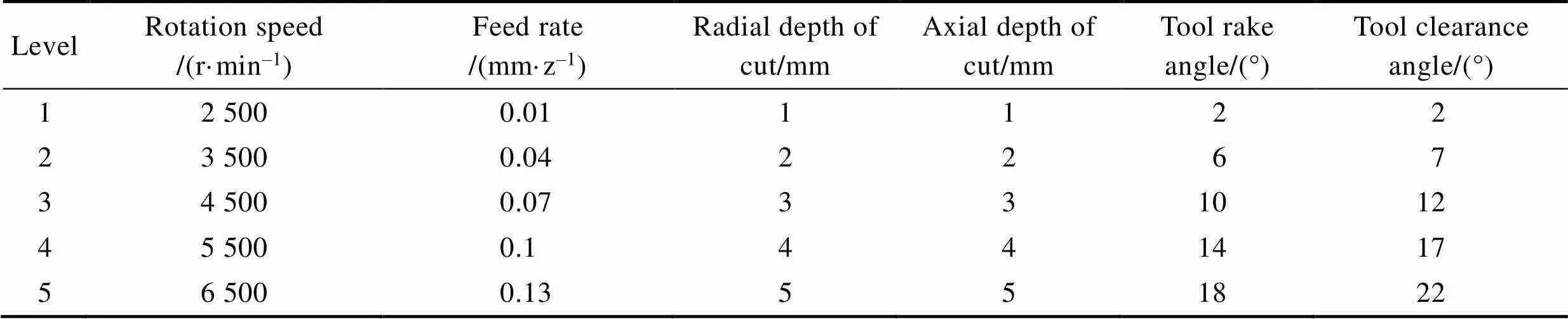
Tab.4 Orthogonal experimental design

表5 25组正交排列和仿真值

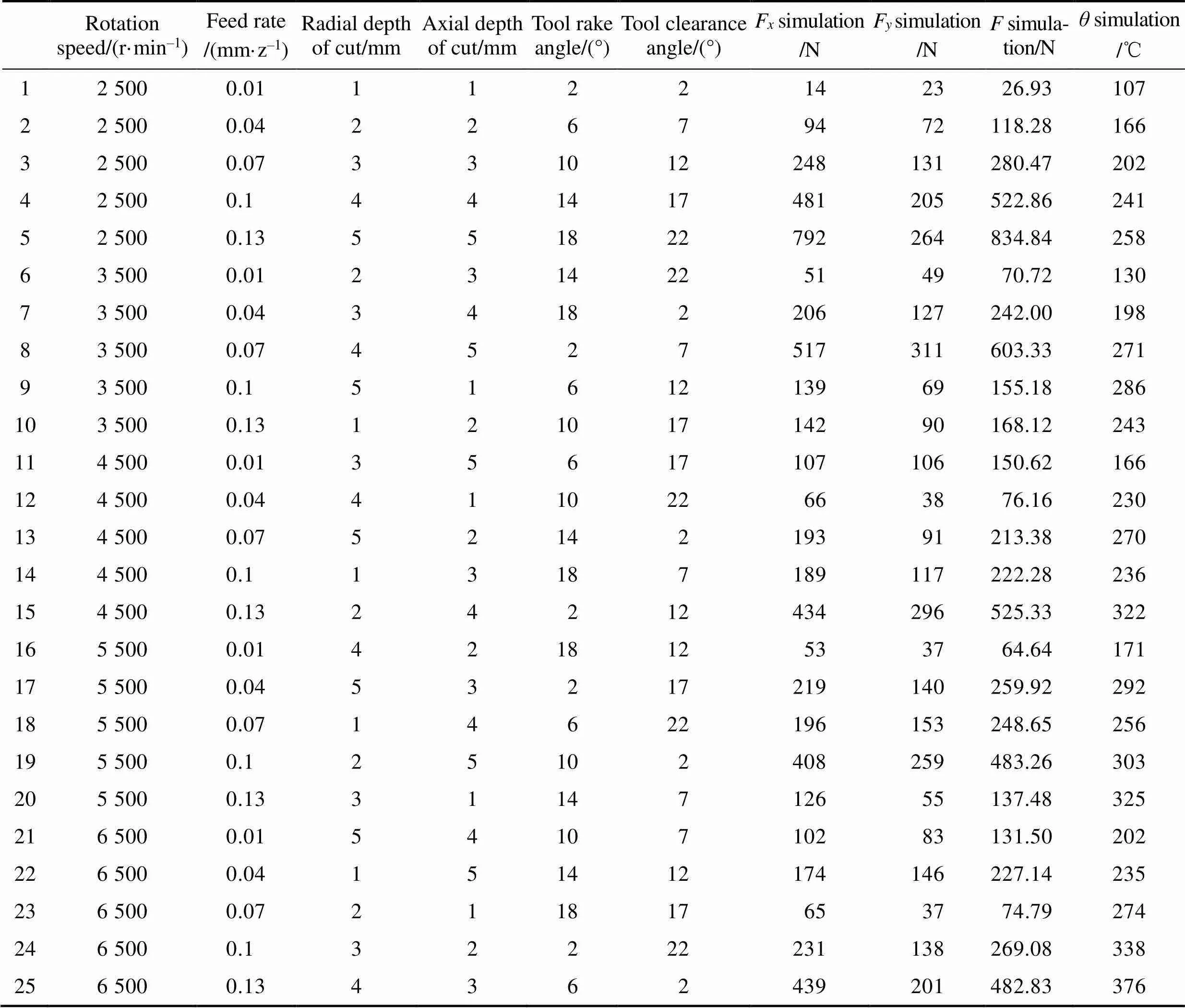
Tab.5 25 groups of orthogonal arrangement and simulation data values

图2 第9组仿真正交试验温度场云图

为更好地评判单个铣削参数和刀具几何参数对铣削力和刀具铣削温度的影响，本文进行了显著性分析。在表5中25组仿真值的基础上，加入了25组函数预测值，对以上50组数值进行方差分析，进而求解出每个参数对铣削力和刀具铣削温度的显著性贡献率，见表6、表7和表8。可以看出，铣削参数中的进给量和轴向切深对铣削力F和F的影响最大，而前角和后角等刀具几何参数对铣削力的影响则相对较小，但这种影响仍然不容忽视，刀具几何参数对铣削力和刀具铣削温度的综合贡献率分别为0.063（F）、0.112 9（F）、0.045 7（）。它们与铣削参数产生强烈的交互作用（如图3所示），共同影响着铣削力和刀具铣削温度，充分表明本文在铣削参数基础上引入刀具几何参数进行仿真分析的合理性。

表6 6个参数对F的贡献率

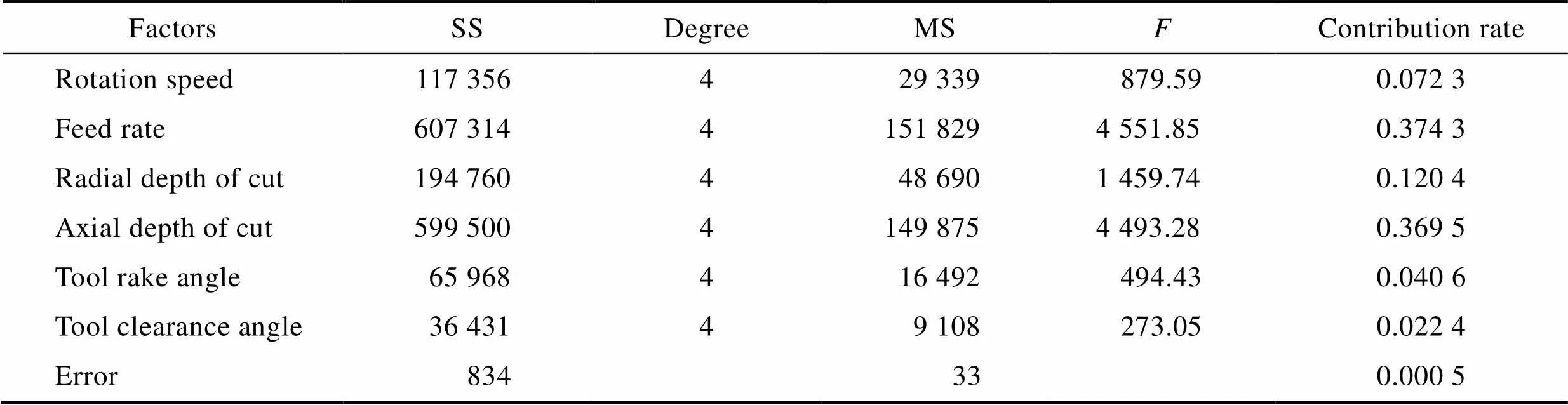
Tab.6 Contributions of six factors to Fx

表7 6个参数对F的贡献率

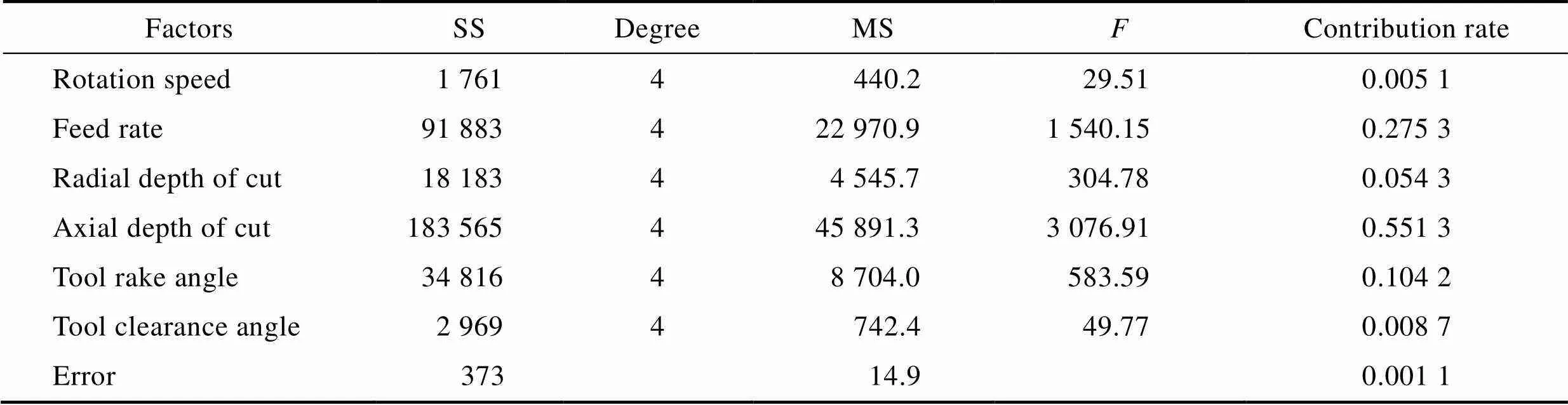
Tab.7 Contributions of six factors to Fy

表8 6个参数对的贡献率

Tab.8 Contributions of six factors to θ

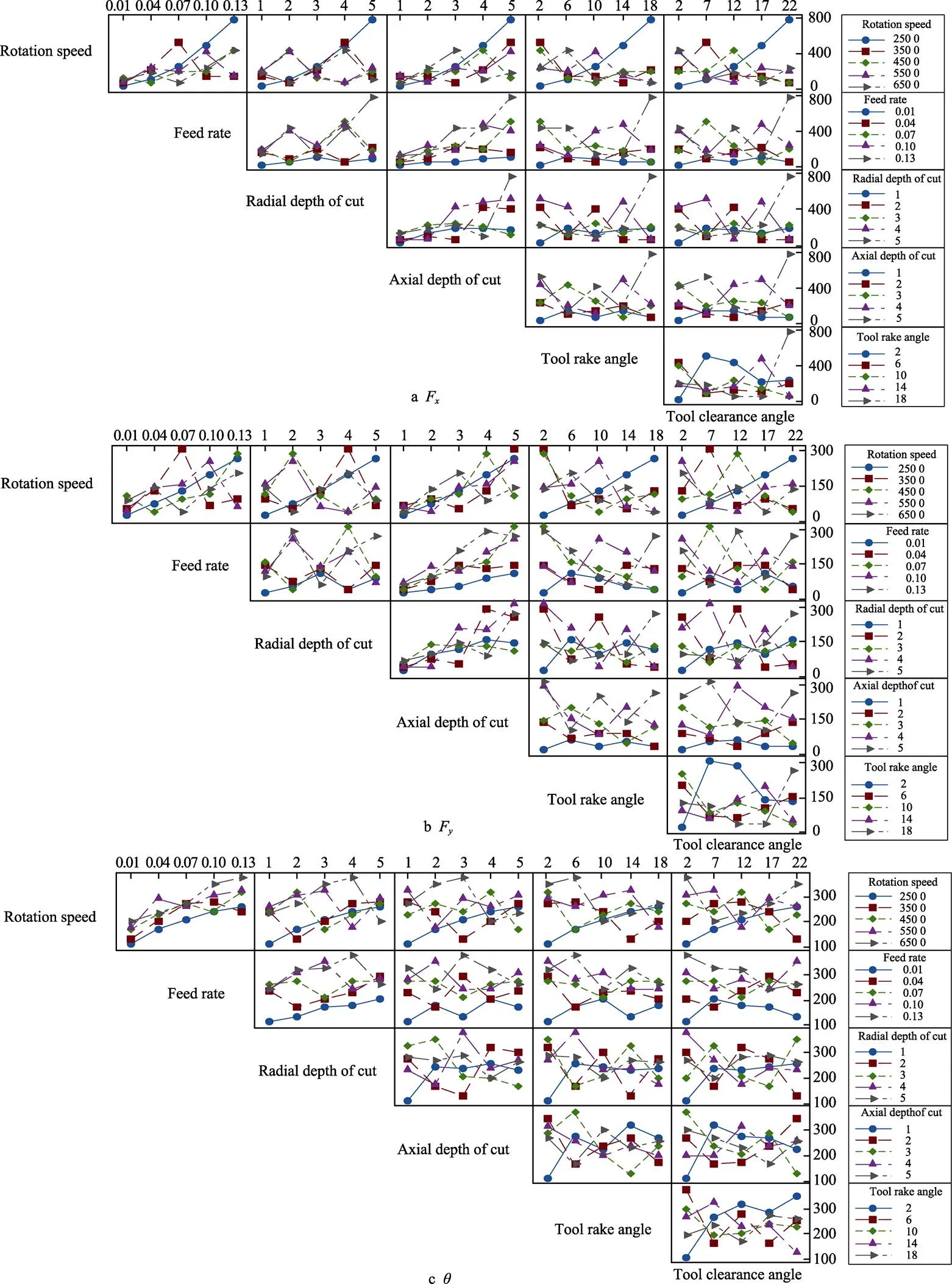
图3 6个参数间的交互作用

1.2 铣削力和刀具铣削温度仿真

为获悉铣削参数和刀具几何参数6个参数对铣削力和刀具铣削温度的交互影响规律，本文在传统铣削参数单因素仿真分析的基础上，增加了对刀具几何参数的单因素分析，如图4所示。该仿真结果的铣削条件：转速为4000 r/min、进给量为0.08 mm/z、径向切深为3 mm、轴向切深为3 mm、刀具前角为10°、刀具后角为14°。

由图4a可以看出，随着铣刀前角的增加，铣削力和刀具铣削温度都会有所降低。这是因为在铣削过程中，刀具前角增大，刀具更为锋利，切割金属材料时，金属变形减小，产生的热量较少，所以铣削力和铣削温度降低。

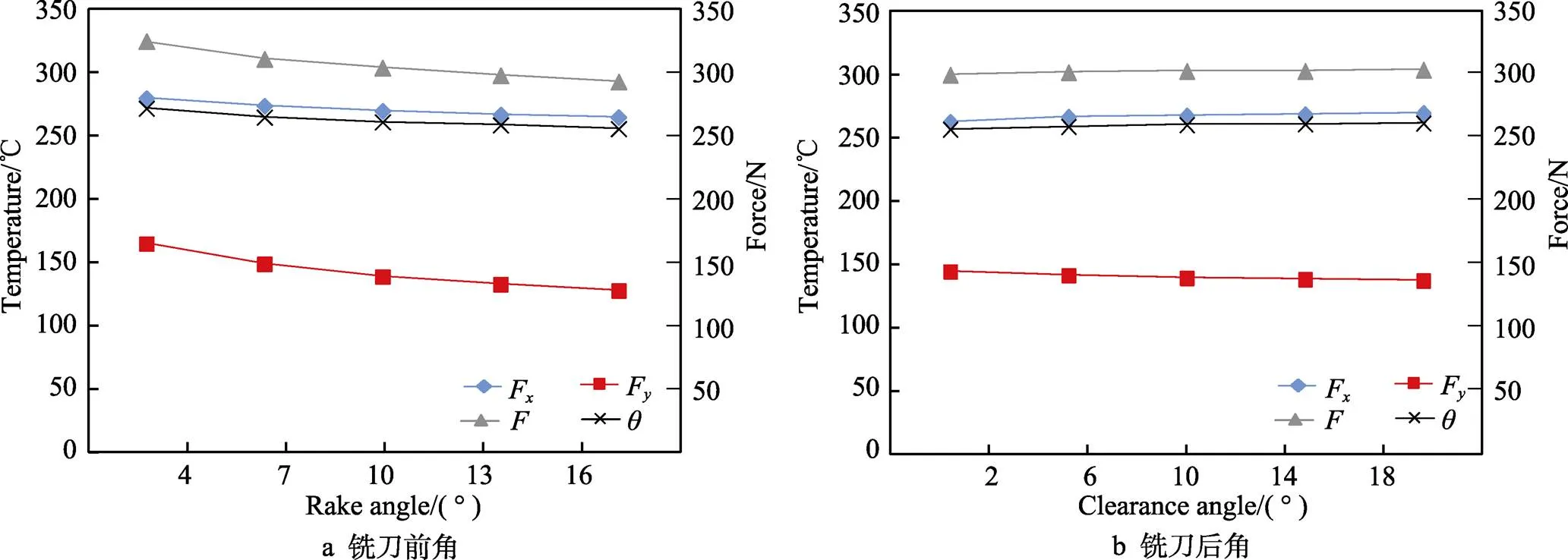
图4 单因素条件下不同刀具几何参数的铣削力和刀具铣削温度仿真值

由图4b可以看出，随着铣刀后角的增加，总铣削力和刀具铣削温度只是稍有变化，说明铣刀后角对于铣削力和刀具铣削温度的影响不大。刀具铣削温度在前刀面和刀尖处最高，后角的作用是减小刀具后刀面和已加工表面的摩擦，提高刀具寿命和提高加工质量。也可能是后角增大后，刀刃变薄，造成刀具自身的热传导能力下降，热量在刀具聚集，所以刀具切削温度稍有上升。

2 铣削参数和刀具几何参数优化模型

在7075-T651铝合金材料铣削仿真时，按表1和表2所列材料的J-C本构参数和J-C损伤参数，建立有限元铣削仿真模型，应用有限元铣削仿真结果中获得的铣削力值和刀具铣削温度值，分别使用回归分析方法建立铣削力和刀具铣削温度关于铣削参数和刀具几何参数的数学模型。相较于传统的最小二乘回归方法，偏最小二乘回归方法（PLS）能够在自变量存在严重多重相关性的条件下进行回归建模运算，因此本文采用了PLS方法进行回归分析，以便能更好地保证回归模型的准确性。

2.1 回归方程的选定

常规的回归方程选定方法使用铣削力和铣削温度的经验公式描述铣削力和铣削温度的变化趋势，见式（3）和式（4）。

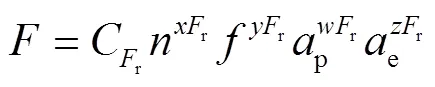
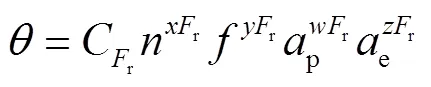
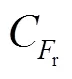
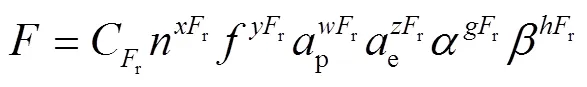
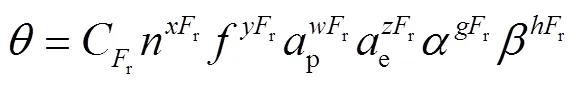
2.2 铣削力与刀具铣削温度建模

因为式（5）、（6）为指数方程形式，可在方程两边同时取对数，将两式分别转换为线性回归方程：

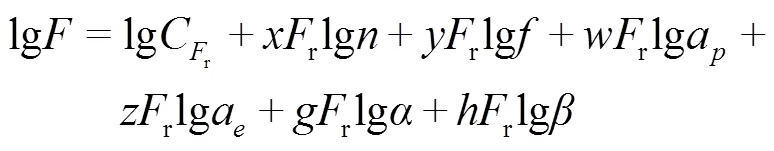
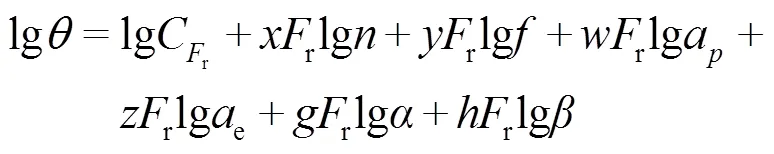
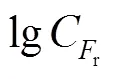
将样本数量扩充至个（如本文中的样本数量为25个），可获得扩展后的样本空间矩阵，令：

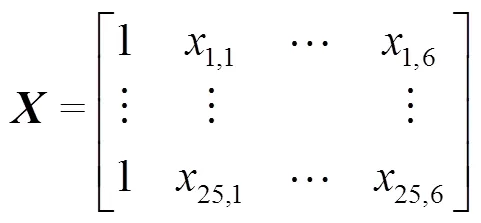
使用偏最小二乘法进行回归分析时，假定有个因变量和个自变量（本文共25个自变量和因变量），为了研究这些因变量与自变量的统计关系，可观测获得的个样本，最终分别形成关于自变量、因变量的数据表（为包含自变量的表）和（为包含因变量的表）。在与中分别提取出和，要求：和应尽可能大地携带它们各自数据表中的信息；和的相关程度能够达到最大。

当提取样本空间中的第一个样本后，使用偏最小二乘回归分别实施对的回归以及对的回归。如果回归方程已经达到满意的精度，则算法终止；否则，将利用被解释后的残余信息以及被解释后的残余信息进行样本空间的第二个样本提取。如此往复，直到能达到一个较满意的精度为止，然后再表达出关于原自变量的线性回归方程，最后需将线性回归方程再变换为指数回归方程。

基于专业统计分析类软件Minitab得到了线性回归方程，最后经指数变换得到铣削力和刀具铣削温度关于铣削参数和刀具几何参数的偏最小二乘回归方程：

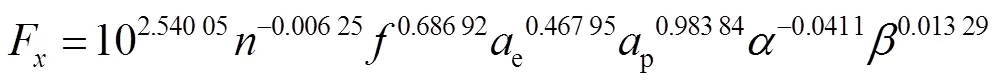
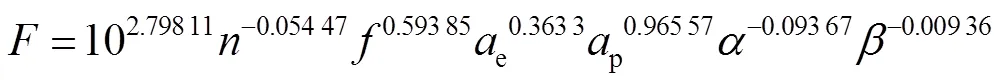
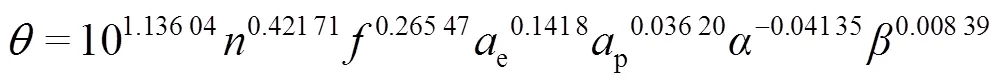
2.3 铣削力和刀具铣削温度模型的试验验证

通过六因素五水平正交仿真试验和偏最小二乘回归，得到了在正交排列表范围内时铣削参数和刀具几何参数到铣削力和刀具铣削温度的数学模型。使用铣削力和刀具铣削温度函数公式（式（10）—式（13））对25组正交排列组合的铣削力和刀具铣削温度进行预测，预测值见表9。

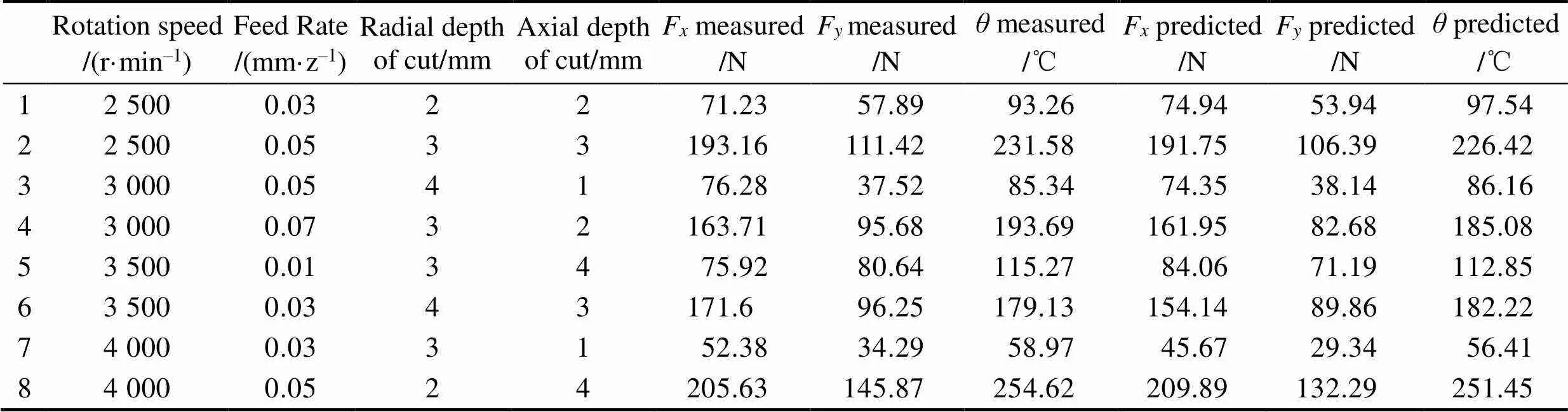
为验证回归函数模型的正确性，设计了8组试验，使用五轴数控加工中心进行7075-T651铝合金材料的铣削加工，使用硬质合金YG8铣刀（三刃、前角15°、后角10°），采用瑞士Kistler测力仪进行铣削力的测量和ABOSUD高精度红外测温仪进行刀具铣削温度的测量。试验测量获得的8组数据结果见表10，这8组实测数值与函数预测值的对比如图5所示。

表9 25组函数预测值

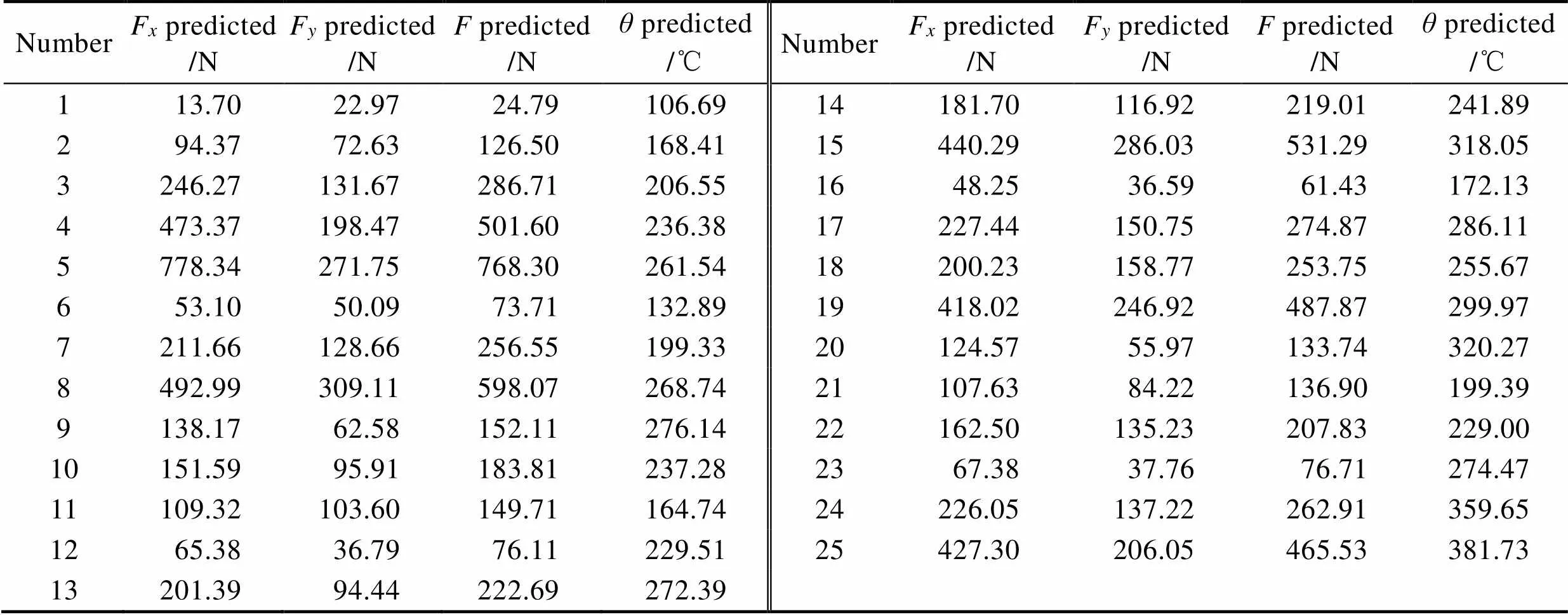
Tab.9 Predicted values of 25 groups of functions

表10 8组试验验证值

Tab.10 Validation values of 8 groups of experiments

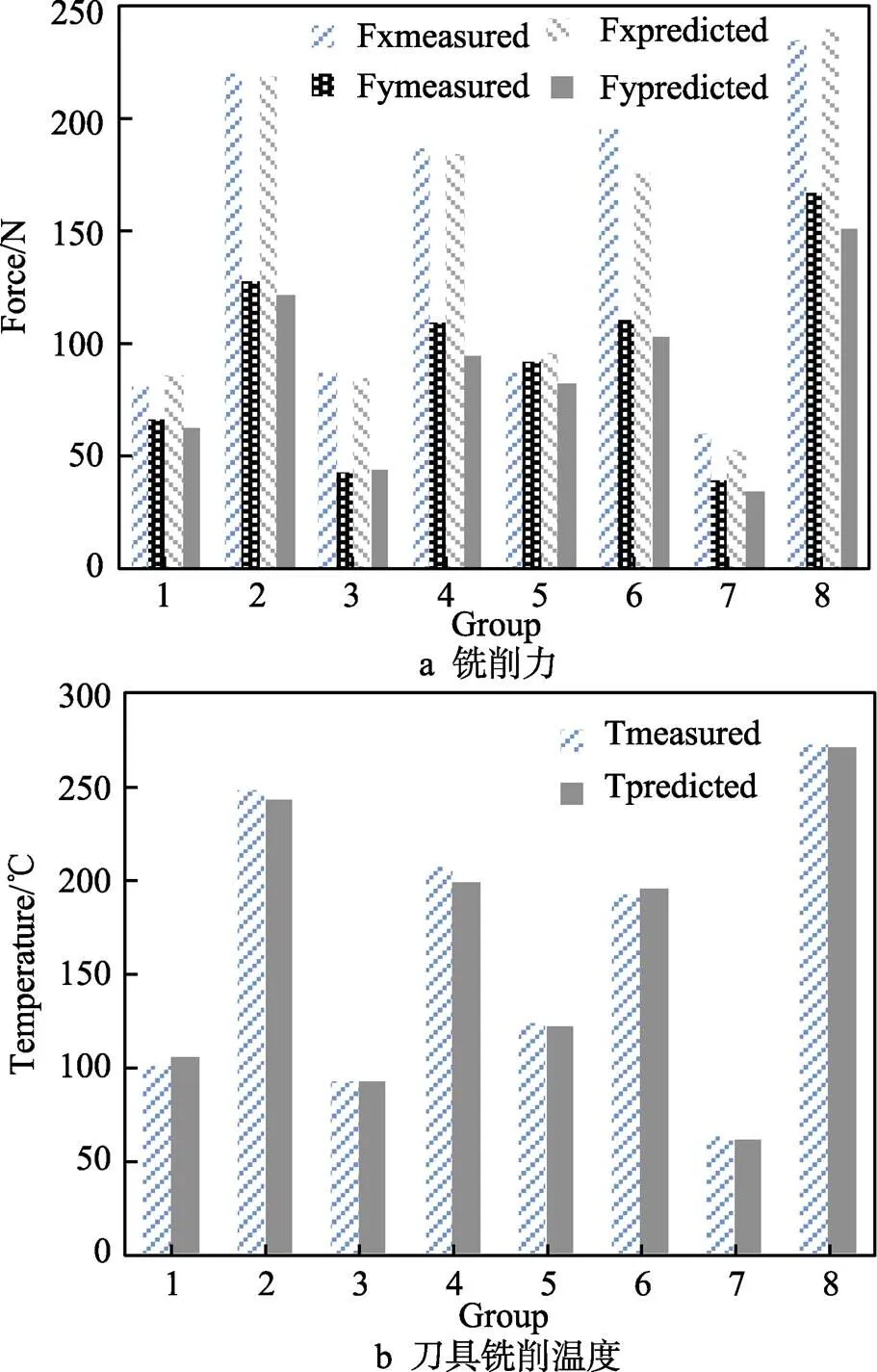
图5 8组实测数据与函数预测数据对比

上述试验测量值与函数预测值的最大差值均没有超过10%，可以认为关于铣削参数和刀具几何参数的偏最小二乘回归方程对铣削力和刀具铣削温度的预测准确可行。

3 多目标优化铣削参数和刀具几何参数

优化问题大多数是多目标优化问题[19-21]。一般情况下，多目标优化问题的各个子目标之间是矛盾的，一个子目标的改善有可能会引起另一个或者另几个子目标的性能降低，也就是要同时使多个子目标一起达到最优值是不可能的，而只能在它们中间进行协调和折中处理，使各个子目标都尽可能达到最优化。多目标优化问题与单目标优化问题的本质区别在于：它的解并非唯一，而是存在一组由众多Pareto最优解组成的最优解集合，该集合中的每个元素称为Pareto最优解或非劣最优解。多目标优化问题的数学表达形式可描述为：

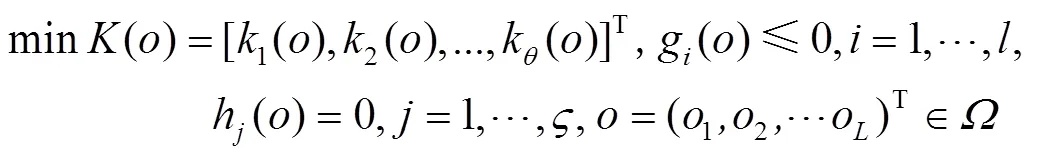
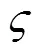
3.1 多目标同步优化与可视化

本文提出的同步优化多目标为：更小的铣削力、更低的刀具铣削温度和更高的金属去除率（为了统一多目标优化为最小值，金属去除率取负值），其数学描述和约束条件为：

设铣刀齿数为，铣刀直径为，铣削速度=π/1 000，则金属去除率的计算公式为：

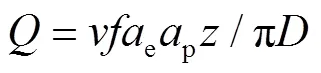
将式（14）变化为：

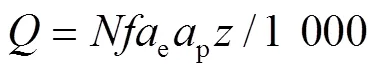
以上数学描述具有4个目标函数，无法通过三维可视化显示，这对于本文优化结果的评定造成了困难。针对薄壁件加工过程中，变形主要集中在径向方向上，由于引起工件变形的切削力沿工件厚度方向，90%的变形是由引起的，因此在进行薄壁件加工仿真时，大多只输入F，变形仿真准确率同样可以达90%[22-23]。鉴于此，可以忽略掉目标，转变为3个目标函数。在多目标优化领域主要有8种多目标优化算法：NSGA-Ⅱ、SPEA2、NSGA-Ⅲ、MOPSO、GDE3、AGE-MOEA、SRA、VaEA（Vector angle-based Evolutionary Algorithm）[24]。为了挑选出适合本文拟解决问题的多目标优化算法，对以上8种典型优化算法进行对比分析，算法设置均为200个种群，迭代500代。其中，NSGA-Ⅱ、SPEA2、NSGA-Ⅲ、AGE- MOEA的交叉概率为0.9，变异概率为0.1；GDE 3算法的CR参数和CF参数分别为0.8和0.5；MOPSO中的学习因子1、2均取为1.5，惯性常量取0.8；SRA中的随机排序参数c为0.5；VaEA的参数比率取0.01。各种算法的Pareto前沿如图6所示，各种算法独立运行30次的平均耗时如图7所示。

综合分析图6和图7可知，NSGA-II和NSGA-III作为典型非支配排序遗传算法，在解决本文多目标优化问题时，并没能生成完整的Pareto前沿曲面，获得的解仅在1～2个目标的最优值处拥挤排布，无法获得3个目标的最优值。GDE3虽然生成了众多解，但同样拥挤在单个目标最优值处，没有生成完整的Pareto前沿曲面。SPEA2、MOPSO、VaEA、SRA和AGE-MOEA生成了比较完整的Pareto前沿曲面，但其中MOPSO、AGE-MOEA和SRA获得的解的分布性稍差，SPEA2和AGE-MOEA耗费的计算时间较多。VaEA不但生成了比较完整的Pareto前沿曲面，其解具有良好的分布性，同时计算解的耗时居于中位。

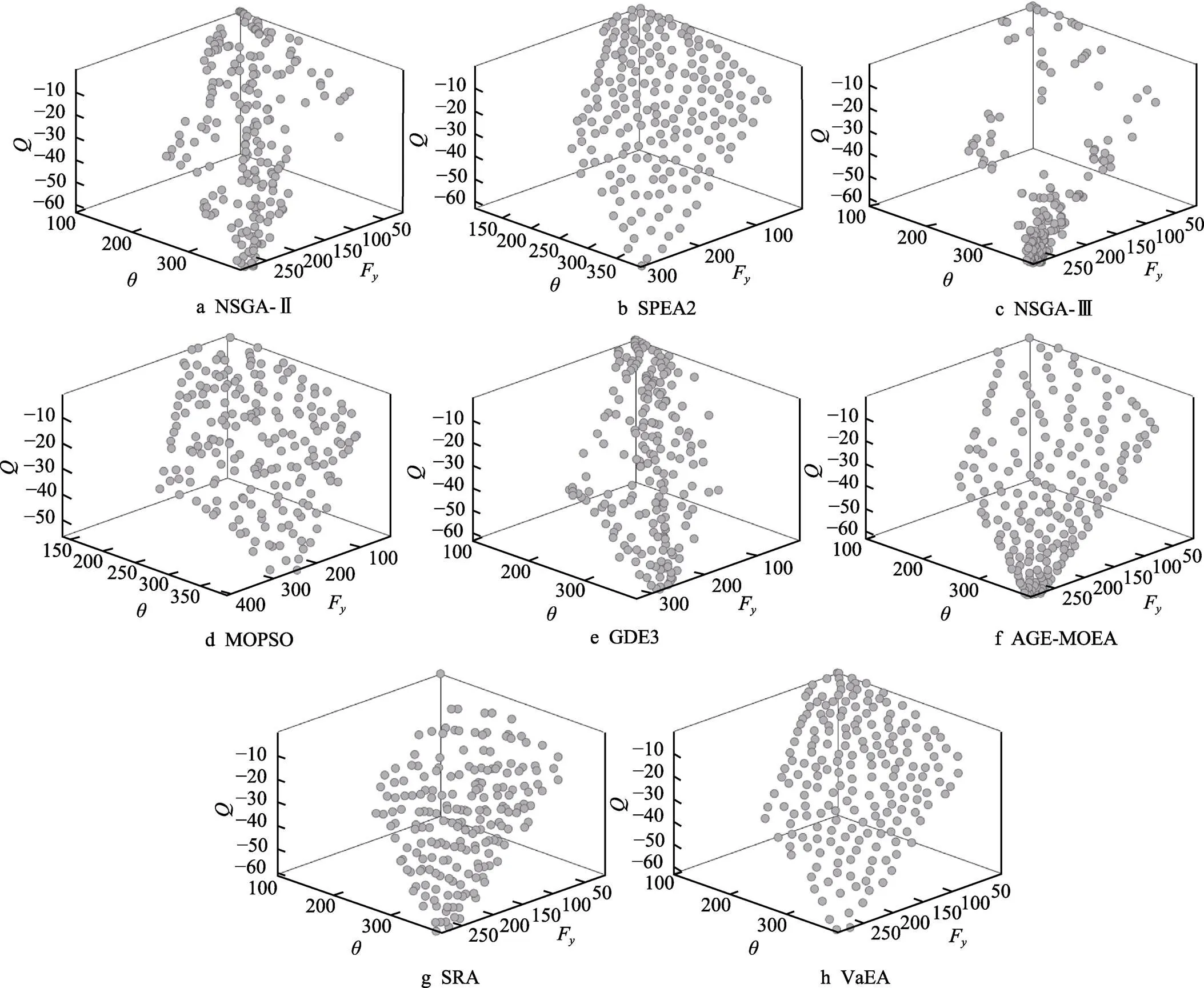
图6 8种算法的Pareto前沿曲面

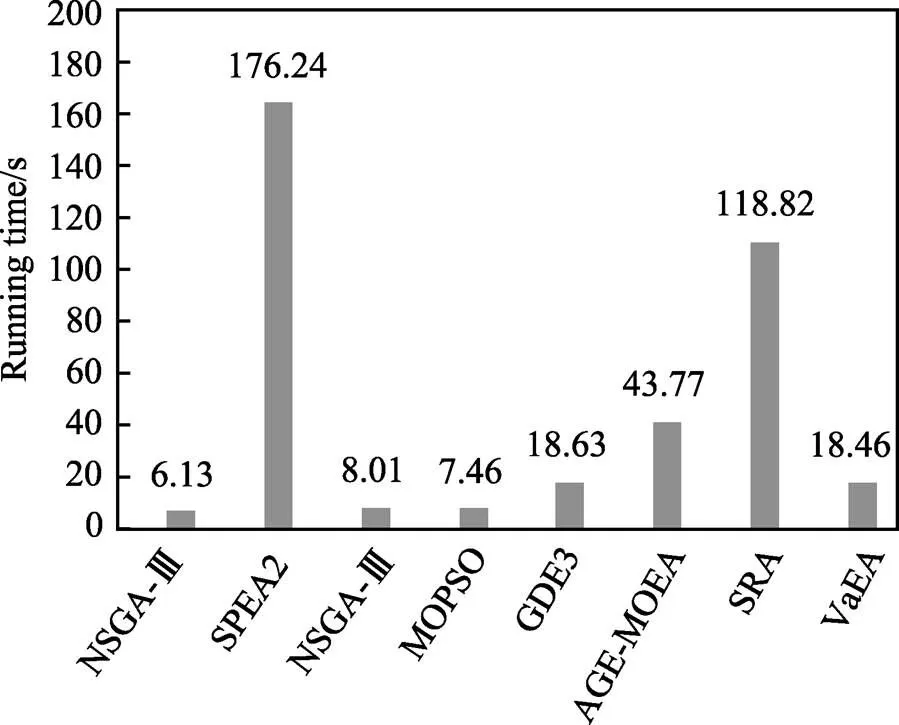
图7 算法耗时

3.2 HV性能指标评价

为了更好地评定各种算法在本文多目标优化方面的性能，本文引入了超体积指标（HV，Hypervolume）。HV指标评价方法最早是由Zitzler等[25]提出，它表示由解集中的个体与参考点在目标空间中所围成的超立方体的体积，它是一种与Pareto一致的评价方法。也就是说，如果一个解集优于另一个解集′，那么解集的HV指标亦会大于解集'的HV指标。这同时也意味着HV值越大，算法的综合性能越好。HV指标评价方法可以同时评价算法的收敛性和多样性，并且无需知道Pareto前沿或参考集，多用于高维多目标优化问题。HV指标公式为：

式（13）中：表示Lebesgue测度，用来测量体积；表示非支配解集的数目；v表示参照点与解集中第个解构成的超体积。

应用HV性能评价各种算法在独立计算30次后的最好值（HV best）和平均值（HV average）如图8所示。由图8可以看出，无论是HV best还是HV average，VaEA在8种算法中的HV指标均最大。

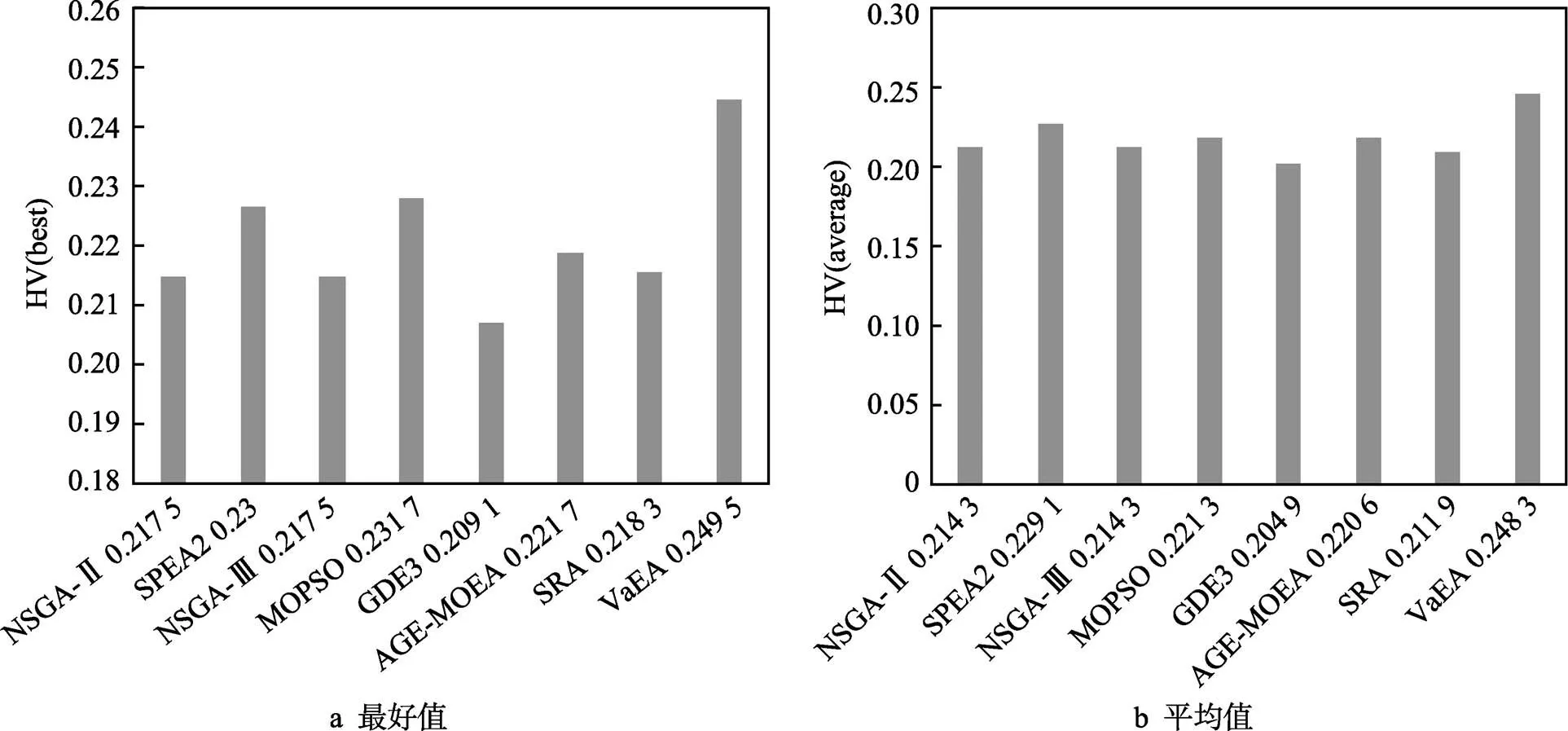
图8 HV指标值

3.3 优化结果提取分析

经过对铣削力、刀具铣削温度和金属去除率3个目标优化Pareto前沿曲面可视化对比和HV指标评定，综合考虑，可以使用VaEA算法处理本文的多目标优化问题。使用VaEA算法提取多目标优化后的部分结果见表11。结果表明，为提高7075-T651铝合金工件的铣削加工效率，可使用表11中第3、4组的铣削参数和刀具几何参数；为提高7075-T651铝合金工件的铣削加工质量，可使用表11中第1、2组的铣削参数和刀具几何参数；为获得金属去除率、铣削力、刀具铣削温度间的平衡，可使用表11中第5、6组的铣削参数和刀具几何参数。

表11 部分优化结果

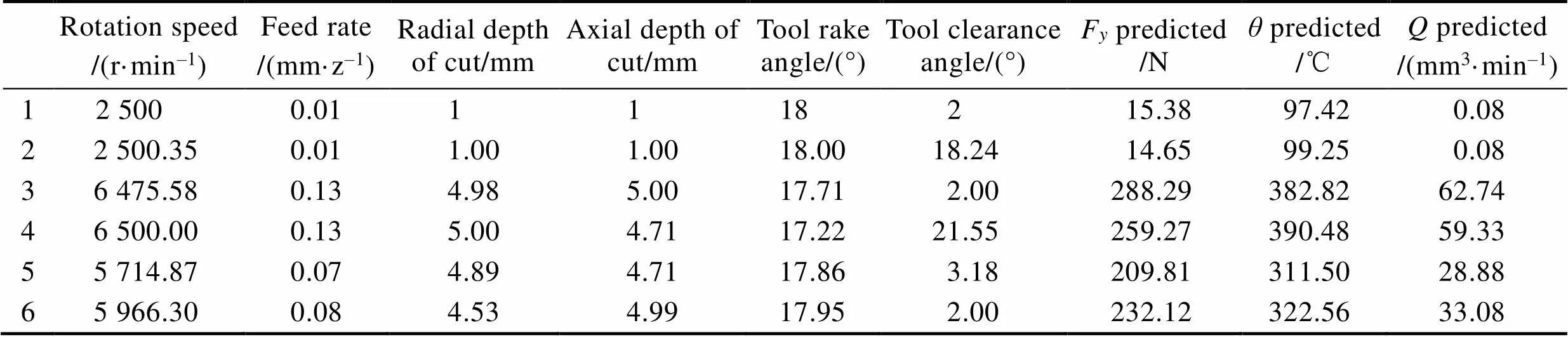
Tab.11 optimization results

4 结语

基于对单一目标的单因素分析和正交实验并结合偏最小二乘法回归模型，可以建立2类参数（铣削参数和刀具几何参数）到3个目标（铣削力、刀具铣削温度和金属去除率）的函数关系。分别利用8种典型的多目标优化算法对本文提出的2类参数、3个目标优化问题进行优化求解，并分别实现三维Pareto前沿曲面可视化，结合可视化结果和指标评价的综合分析，结果表明，VaEA优化算法的Pareto解分布比较均匀、具有优越的Pareto前沿曲面和性能指标，更适合作为求解本文多目标优化问题的优化算法。提取VaEA算法优化计算获得的铣削参数和刀具几何参数组合，可实现对不同铣削目标的优化控制，表明将VaEA算法用于本文铣削参数和刀具几何参数的多目标优化是可行的，在降低7075-T651铝合金工件铣削时的铣削力、铣削温度，并提高金属去除率等方面具有实际应用价值。

[1] DUAN Zhen-jing, LI Chang-he, DING Wen-feng, et al. Milling Force Model for Aviation Aluminum Alloy: Aca­demic Insight and Perspective Analysis[J]. Chinese Jour­nal of Mechanical Engineering, 2021, 34: 18-52.

[2] 岳修杰, 张平, 宋爱利, 等. 7075铝合金高速铣削表面质量及刀具磨损机理[J]. 有色金属工程, 2021, 11(2): 9- 16.

YUE Xiu-jie, ZHANG Ping, SONG Ai-li, et al. Study on Surface Quality and Tool Wear Mechanism of High- Speed Cutting of 7075 Aluminum Alloy[J]. Nonferrous Metals Engineering, 2021, 11(2): 9-16.

[3] MA Wei, WANG Rong-qi, ZHOU Xiao-qin, et al. The Finite Element Analysis-Based Simulation and Artificial Neural Network-Based Prediction for Milling Processes of Aluminum Alloy 7050[J]. Proceedings of the Institu­tion of Mechanical Engineers, Part B: Journal of Enginee­ring Manufacture, 2021, 235(1-2): 265-277.

[4] RAMNATH R A, THYLA P R, HARISHSHARRAN A K R. Machining Parameter Selection in Milling Epoxy Gra­ni­te Composites Based on AHP[J]. Materials Today: Proceedings, 2021, 42: 319-324.

[5] 邓聪颖, 杨凯, 苗建国, 等. 基于加工位置不确定的多工步数控铣削工艺参数优化研究[J]. 仪器仪表学报, 2020, 41(4): 111-118.

DENG Cong-ying, YANG Kai, MIAO Jian-guo, et al. Process Parameters Optimization of Multi-Pass CNC Mil­ling Considering Uncertain Machining Position[J]. Chine­se Journal of Scientific Instrument, 2020, 41(4): 111-118.

[6] 李体仁, 王心玉, 马超超. 基于混沌粒子群算法的钛合金薄壁筋铣削变形优化[J]. 组合机床与自动化加工技术, 2020(1): 59-63.

LI Ti-ren, WANG Xin-yu, MA Chao-chao. Milling Defor­med Optimization of Titanium Alloy Thin Wall Bars Based on Chaotic Particle Swarm Optimization[J]. Modu­lar Machine Tool & Automatic Manufacturing Technique, 2020(1): 59-63.

[7] 胡瑞飞, 殷鸣, 刘雁, 等. 切削稳定性约束下的铣削参数优化技术研究[J]. 机械工程学报, 2017, 53(5): 190- 198.

HU Rui-fei, YIN Ming, LIU Yan, et al. Optimization of Milling Parameters under Constrain of Process Stabi­lity[J]. Journal of Mechanical Engineering, 2017, 53(5): 190-198.

[8] SAGLAM H, UNSACAR F, YALDIZ S. Investigation of the Effect of Rake Angle and Approaching Angle on Main Cutting Force and Tool Tip Temperature[J]. International Journal of Machine Tools and Manufacture, 2006, 46(2): 132-141.

[9] 潘永智, 艾兴, 唐志涛, 等. 基于切削力预测模型的刀具几何参数和切削参数优化[J]. 中国机械工程, 2008, 19(4): 428-431.

PAN Yong-zhi, AI Xing, TANG Zhi-tao, et al. Optimiza­tion of Tool Geometry and Cutting Parameters Based on a Predictive Model of Cutting Force[J]. China Mechanical Engineering, 2008, 19(4): 428-431.

[10] YI Jiao-hong, XING Li-ning, WANG Gai-ge, et al. Beha­vior of Crossover Operators in NSGA-III for Large-Scale Optimization Problems[J]. Information Sciences, 2020, 509: 470-487.

[11] 齐红, 任洪娥, 贾鹤鸣, 等. 基于改进PSO神经网络的微米木纤维切削参数优化[J]. 中山大学学报(自然科学版), 2018, 57(2): 116-122.

QI Hong, REN Hong-e, JIA He-ming, et al. Optimization Study of Cutting Parameters of Micron Wood Fiber Based on Improved PSO Neural Network[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2018, 57(2): 116- 122.

[12] 赵荣荣. 基于人工神经网络的铣削参数优化研究[D]. 西安: 西安建筑科技大学, 2015.

ZHAO Rong-rong. Studies on Milling Parameters Opti­mi­za­tion Based on Artificial Neural Network[D]. Xi'an: Xi'an University of Architecture and Technology, 2015.

[13] 徐玲, 杨丹, 王时龙, 等. 基于进化神经网络的刀具寿命预测[J]. 计算机集成制造系统, 2008, 14(1): 167-171.

XU Ling, YANG Dan, WANG Shi-long, et al. Prediction of Cutting Tool Life Based on Evolutionary Neural Net­work[J]. Computer Integrated Manufacturing Systems, 2008, 14(1): 167-171.

[14] 李许庆, 石艳, 胥云, 等. 基于NSGA-Ⅱ的航发叶片粗铣加工工艺参数优化研究[J]. 组合机床与自动化加工技术, 2020(9): 162-166.

LI Xu-qing, SHI Yan, XU Yun, et al. Study on the Opti­mization of Rough Milling Process Parameters of Aeroen­gine Blades Based on NSGA-Ⅱ[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2020(9): 162-166.

[15] 岳彩旭, 刘鑫, 刘智博, 等. 基于有限元仿真的拼接模具铣削用刀具优化[J]. 中国机械工程, 2020, 31(17): 2085-2094.

YUE Cai-xu, LIU Xin, LIU Zhi-bo, et al. Tool Optimi­zation for Splicing Die Milling Processes Based on Finite Element Simulation[J]. China Mechanical Engineering, 2020, 31(17): 2085-2094.

[16] AY M. Effect of Cutting Parameters on Surface Rough­ness, Tool Temperature and Vibration in Turning of AISI 316 Ti Stainless Steel[J]. Materials Testing, 2019, 61(1): 71-79.

[17] ABDELNASSER E, BARAKAT A, ELSANABARY S, et al. Precision Hard Turning of Ti6Al4V Using Polycrystal­line Diamond Inserts: Surface Quality, Cutting Tempera­ture and Productivity in Conventional and High-Speed Machining[J]. Materials (Basel, Switzerland), 2020, 13(24): 56-77.

[18] 栗方. 多目标优化算法标准测试函数寻优研究[J]. 电脑知识与技术, 2020, 16(23): 203-206.

LI Fang. Research on Standard Test Function Optimiza­tion of Multi-Objective Optimization Algorithm[J]. Com­puter Knowledge and Technology, 2020, 16(23): 203-206.

[19] JIANG Shou-yong, YANG Sheng-xiang. A Strength Pa­re­to Evolutionary Algorithm Based on Reference Direction for Multiobjective and Many-Objective Optimization[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(3): 329-346.

[20] 冯茜, 李擎, 全威, 等. 多目标粒子群优化算法研究综述[J]. 工程科学学报, 2021, 43(6): 745-753.

FENG Qian, LI Qing, QUAN Wei, et al. Overview of Multiobjective Particle Swarm Optimization Algorithm[J]. Chinese Journal of Engineering, 2021, 43(6): 745-753.

[21] 岳彩通, 梁静, 瞿博阳, 等. 多模态多目标优化综述[J]. 控制与决策, 2021, 36(11): 2577-2588.

YUE Cai-tong, LIANG Jing, QU Bo-yang, et al. A Survey on Multimodal Multiobjective Optimization[J]. Control and Decision, 2021, 36(11): 2577-2588.

[22] 刘建宁, 李占锋, 司宇. 一种航空薄壁件铣削加工变形补偿算法[J]. 组合机床与自动化加工技术, 2015(11): 33-36.

LIU Jian-ning, LI Zhan-feng, SI Yu. A Method of Ma­chining Deformation Compensation for Aeronautical Thin-Walled Parts[J]. Modular Machine Tool & Auto­matic Manufacturing Technique, 2015(11): 33-36.

[23] 韩振宇, 金鸿宇, 付云忠, 等. 基于有限元数值模型和进给速度优化的薄壁件侧铣变形在线控制[J]. 机械工程学报, 2017, 53(21): 190-199.

HAN Zhen-yu, JIN Hong-yu, FU Yun-zhong, et al. FEM Numerical Model and Feedrate Optimization Based On- Line Deflection Control of Thin-Walled Parts in Flank Milling[J]. Journal of Mechanical Engineering, 2017, 53(21): 190-199.

[24] XIANG Yi, ZHOU Yu-ren, LI Mi-qing, et al. A Vector Angle-Based Evolutionary Algorithm for Unconstrained Many-Objective Optimization[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(1): 131-152.

[25] ZITZLER E, THIELE L, LAUMANNS M, et al. Perfor­mance Assessment of Multiobjective Optimizers: An Analysis and Review[J]. IEEE Transactions on Evolu­tionary Computation, 2003, 7(2): 117-132.

Multi-objective Synchronous Optimization Method for Milling Parameters and Tool Geometric Parameters of 7075-T651 Aluminum Alloy

1,2,1

(1. School of Mechanical Engineering, Tiangong University, Tianjin 300387, China; 2. College of Mechanical and Control Engineering, Guilin University of Technology, Guangxi Guilin 541006, China)

This paper aims to reduce the milling force and milling heat in order to reduce the deformation of the 7075-T651 aluminum alloy workpiece and improve the metal removal rate. In this paper, a method for simultaneous optimization of two kinds of parameters (milling parameters and tool geometric parameters: rotation speed, feed rate, radial depth of cut, axial depth of cut, rake angle and clearance angle) was proposed, which could achieve multiple objectives (milling force, tool milling temperature and metal removal rate). Based on the partial least squares regression model and the finite element simulation results of milling 7075-T651 aluminum alloy workpiece, the functional relationship model between milling force and tool milling temperature and metal removal rate of two types of parameters were established, and 8 typical multi-objective optimization algorithms were used to solve the above models. By visualizing the Pareto front surface and HV performance index, the optimal solution algorithm that can solve the problems in this paper was screened. The optimal solution values of milling parameters and tool geometric parameters were obtained, such as rotational speed 5 966.30 r/min, feed 0.08 mm/z, radial cutting depth 4.53 mm, axial cutting depth 4.99 mm and rake angle 17.95°, clearance angle 2.00° for tool geometric parameters. At this time, the corresponding milling force is 232.12 N, tool milling temperature 3 is 22.56 ℃, and the metal removal rate is 33.08 mm3/min). The optimization results can achieve comprehensive control objectives such as lower milling force and milling temperature and higher metal removal rate, and have practical application value in reducing workpiece deformation and improving machining efficiency during milling of 7075-T651 aluminum alloy workpiece.

milling parameters; tool geometric parameters; milling force; milling temperature; multi-objective optimization

TG714

A

1001-3660(2022)04-0263-12

10.16490/j.cnki.issn.1001-3660.2022.04.027

2021-04-27；

2021-10-15

2021-04-27；

2021-10-15

广西自然科学基金（2021GXNSFAA220019）；国家自然科学基金（52075110）

Guangxi Natural Science Foundation (2021GXNSFAA220019); The National Natural Science Foundation of China (52075110)

陈良骥（1978—），男，博士，教授，主要研究方向为复杂曲面CAD/CAM、五轴CNC精密轨迹控制和精密加工。

CHEN Liang-ji (1978—), Male, Doctor, Professor, Research focus: complex surface CAD/CAM, five-axis CNC precision trajectory control and precision processing.

陈良骥, 魏子森. 7075-T651铝合金铣削参数与刀具几何参数的多目标同步优化方法[J]. 表面技术, 2022, 51(4): 263-274.

CHEN Liang-ji, WEI Zi-sen. Multi-objective Synchronous Optimization Method for Milling Parameters and Tool Geometric Parameters of 7075-T651 Aluminum Alloy[J]. Surface Technology, 2022, 51(4): 263-274.

责任编辑：刘世忠