极值点偏移问题的通法探究

广东省湛江一中培才学校(524037) 魏 欣

本文通过2021 年新高考Ⅰ卷、2021 年广州一模和2021年广东一模导数压轴大题解法分析,列出极值点偏移问题在高考中的常考设问形式,总结出极值点偏移问题的通法:构造对称函数法、对数平均值不等式法、差值换元法、比值换元法,并得到与函数F(x)=相关的极值点偏移的性质,对问题与一般性结论的推广,揭示极值点偏移问题的本质.

一、经典试题展示

二、解法探究

题目1 的解法探究

先证x1+x2>2.构造函数g(x)=f(2−x)=(2−x)(1−ln(2−x))(x <2),如图1 虚线所示,下面比较f(x)与g(x)在极值点左侧的大小,令h(x)=f(x)−g(x),(00,故h(x)在(0,1)上单调递增.则h(x)1,2−x1>1,函数f(x) 在(1,+∞)上单调递减,故x2>2−x1,即x1+x2>2 得证.

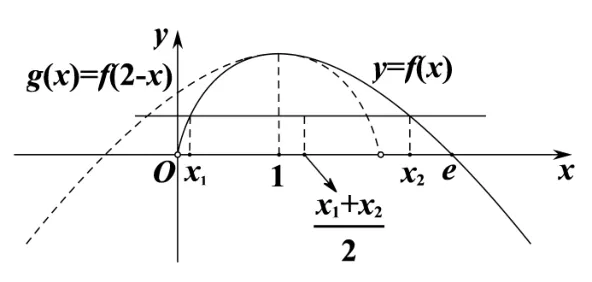
图1

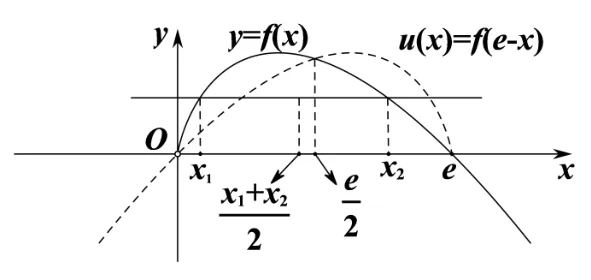
图2

题目2 和3 的解法探究

分析2021 年广州一模第22 题中f(x)=xlnx −ax2+x(a ∈R)有两个零点x1,x2,实质等价于2021 年广东一模第21 题g(x)=lnx −ax+1 有两个零点x1,x2,因此本题的题源实质是下面两个:

图3

三、极值点偏移问题在高考题中的常考设问形式

(一) 极值点偏移问题设问形式

极值点偏移问题在高考中的常考的设问一般有三种形式:函数含参的变化,要证的不等式的变化,对x1,x2作进一步的范围限制.如:

(二) 极值点偏移经典例题

例1 设函数f(x)=lnx −ax,函数f(x)有两个不同的零点x1,x2(x1

四、极值点偏移问题的通法

(一)构造对称函数法

利用构造对称函数法解极值点偏移问题的步骤:

(1)求出函数f(x)极值点x0;

(2)利用对称性构造函数:g(x)=f(2x0−x)(xx0));

(3)证明:f(x)>g(x)(或f(x)

(4) 由单调性脱f:由f(x1)=f(x2)>g(2x0−x2)(或f(x1)=f(x2)2x0(或x1+x2<2x0).

利用构造对称函数法解极值点偏移问题是将自变量转移在极值点同侧,再利用单调性比较大小.如前文用构造对称函数法解2021 年新高考Ⅰ卷第22 题、2021 年广州一模第22 题、2021 年广东一模第21 题.

(二)对数平均值不等式法

(三)差值换元法

依据已知条件f(x1)=f(x2)列方程组,将问题转化为只含x1,x2的双变量问题,再利用差值换元(即t=x2−x1)解题.

(四)比值换元法

依据已知条件f(x1)=f(x2)列方程组,当原函数中含有参数时,通过两方程作差或求和可消去参数,将问题转化为只含x1,x2的双变量问题,再利用比值换元(即t=)解题.

五、极值点偏移问题的相关性质