椭圆焦点三角形内切圆性质与应用

杭州外国语学校(310023) 王金震

椭圆的焦点三角形指的是椭圆上一点与椭圆的两个焦点所连接成的三角形.椭圆的焦点三角形问题,可以将椭圆定义和性质、三角形的几何性质以及解三角形等进行有机结合[1].圆是平面几何中非常重要的研究对象,焦点三角形的内切圆问题对于问题转化能力、几何性质的应用能力、数形结合能力提出了更高维度的要求,是解析几何综合问题重点考察内容之一.

一、椭圆焦点三角形内切圆的重要性质

如图1,椭圆C的标准方程为=1,(a >b >0),F1,F2为椭圆C的左右焦点,P为椭圆上不与左右顶点重合的任意一点,∆PF1F2的内切圆圆心为I与∆PF1F2相切于点D,E,H,设点P的坐标为(x0,y0),点I的坐标为(xI,yI).则有如下性质:

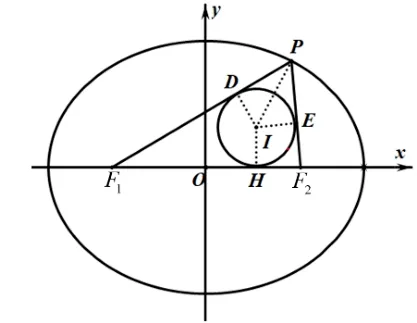
图1

设∆PF1F2的内切圆半径为r,由内切圆性质得IH⊥x轴,当点P在第一象限时则xI=OH,yI=r.根据切线长定理,

性质1 和性质2 的证明采用的是“算两次”的方法.性质1 中对算式(PF1+PF2)−F1F2先利用切线长定理进行化简,再根据椭圆定义进行整理,从而构造方程并求解.性质2 内心横坐标利用切线长定理和椭圆焦半径公式对PF1−PF2算两次构造方程,内心纵坐标利用焦点三角形面积的两种表述算两次求解.

二、椭圆焦点三角形内切圆的重要性质的应用

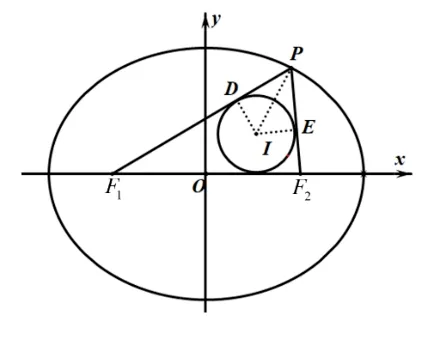
图2

(一)定值问题

例2 已知椭圆=1(a>b>0) 的左右焦点为F1,F2,P为椭圆上不与左右顶点重合的任意一点,I,G分别为∆PF1F2的内心和重心,当IG垂直于x轴时椭圆的离心率为_____.

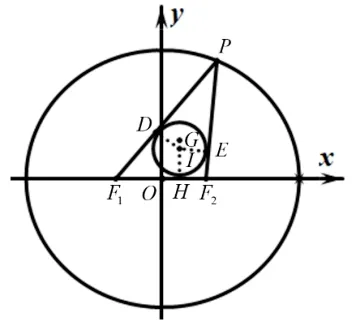
图3

分析本题的难点是对重心和内心进行综合考察.因为性质2 中内心坐标和点P坐标的关系是利用离心率e进行刻画的,所以解决本题的关键是要了解重心和三角形三个顶点之间坐标的数量关系,结合性质2 构造方程求解.

例3 已知椭圆=1左右焦点分别为F1,F2,P为椭圆上一点,∆PF1F2的内心为I,若内切圆半径为1,则|PI|等于

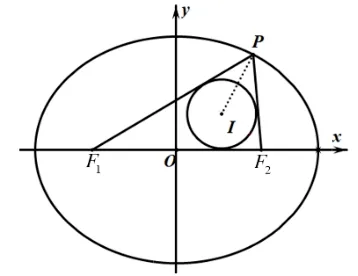
图4

分析本题是对内心坐标和点P坐标关系的直接考察,利用性质2 轻松求解.

(二)轨迹问题

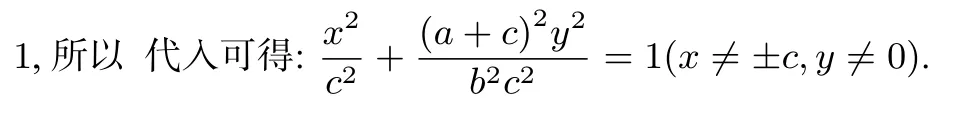
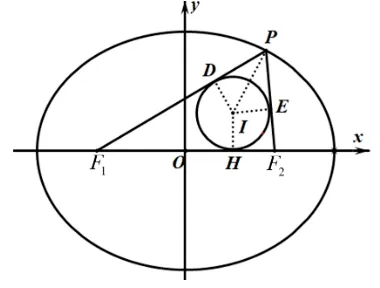
图5

图6

(三)在双曲线上的性质与应用

圆锥曲线的定义、曲线方程、性质存在着诸多联系,很多性质并不是孤立的,所以我们可以试着将椭圆焦点三角形内切圆性质研究思路应用到双曲线中,得到类似的性质.

因为IH⊥x轴,所以F1H=F1O+OH=c+xI.由性质3 得:F1H=a+c=c+xI,即xI=a,性质4 得证.

性质3 和性质4 的证明逻辑同样是利用“算两次”构造方程求解.同理可得,P为双曲线C的左支上异于实轴端点的任意一点,F2D=F2H=a+c,xI=−a.若点P为双曲线C的上异于实轴端点的动点,∆PF1F2内心I的轨迹为x=a或x=−a,且0.

三、结语

解析几何是数学中最有魅力的内容之一,方程是描述曲线性质的语言,曲线又是方程特征的直观体现.圆锥曲线作为解析几何的核心内容,包含特有的对称美和统一美,其离心率是圆锥曲线统一美的集中体现,随着离心率的量变,圆锥曲线的形状也会随之发生质变[2].本文所研究的椭圆的焦点三角形的内心坐标和椭圆上点P的坐标关系同样与离心率相关,展示着圆锥曲线的美妙和神奇.结合椭圆的焦点三角形的重要性质可以解决很多比较棘手的定值问题以及轨迹问题,同样可以将研究方法进行推广来探究双曲线是否也有类似的结论和性质.解析几何的魅力在于本身知识体系的深度、交叉内容的广度以及思想方法的灵活多样,相信随着研究的深入可以得到更多有趣且优美的结论.