一道椭圆中直线过定点问题的探究与溯源

重庆市长寿中学(401220) 田 鹏 王海辉

1 试题呈现

(I)求a的值;

(II) 设线段AF,BF的延长线分别交椭圆于D,E两点,当k变化时,直线DE是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.

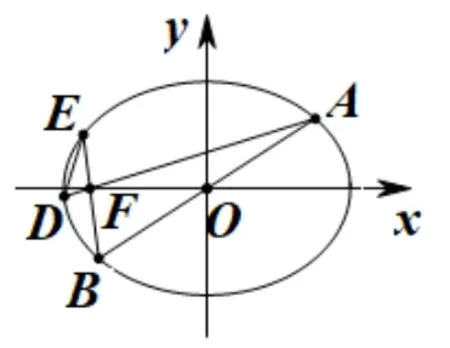
图1

试题着眼于直线与椭圆的位置关系的研究.问题(I)考查基础知识,起点低,结合向量数量积的运算,易得a=问题(II)兼顾基础与创新,“低起点,多层次,高落差”,设计直线过定点问题,与常见的直线过定点问题的类型不尽相同.本题中的图形涉及的点、线较多,这给问题的解决带来了困难.解题过程中数值计算和多字母计算及推理能够很好地检验学生“用代数方法研究几何问题”的能力,有效地考查了学生的逻辑推理能力和数学运算素养,是一道区分度较高的试题.

2 试题解答

评注由对称性不难得到直线DE所过定点在x轴上.解法一依循解决解析几何的通性通法,遵循“设——列——解”的程序化套路.由于解法一根据条件“顺路走”,侧重于将几何位置关系直接代数表示,因而计算量(其中涉及多元代数运算)不可谓不大.欲求证直线DE过定点,理所当然应先求出D,E的坐标,再由直线的点斜式方程求得直线DE的方程,进而求得定点坐标.

评注解法二实际上依赖于解法一中的结论,即直线DE的斜率为直线AB的斜率的5 倍.不同的是解法一注重设点解点,而解法二注重设线整体代换,先假设直线DE的方程为x=my+n,进而寻找m和n的方程关系,求得定点坐标.另外,还得注意n=要舍去.从运算过程来看,解法二比解法一优化了不少,其最关键的就是设而不求的方程思想的运用,可以看出解法二有两个难点,一个是斜率间的关系,另一个是m和n的方程的寻找,如果这个两个难点中的任何一个没有得到解决,要得到最终的结果无疑是困难的.下面我们介绍第三种方法,有目的的寻找方程:

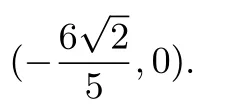
评注解法三构造二次曲线的方法通常适用于圆锥曲线的相交弦的问题,这种解法虽然计算量很大,但是解决问题的目标是很明确的,即寻找直线系数的一次方程关系,进而求得直线过定点.

值得注意的是,从本题的三种解法的解题过程来看,运算量实际上都较大.不过,用代数方法研究几何问题有时候难免运算量较大.因此,在没有更好的方法解决问题时,要求学生鼓起勇气计算下去,培养和提高学生的运算能力与推理能力是很有必要的,这也是培育学生数学运算素养的重要途径.至于本题是否还有更优化的方法,在此先不过多地探讨.

著名数学家波利亚说过:“好问题同某种蘑菇有些相似,它们大都成堆地生长,找到一个以后,你应当再在周围找一找,很可能在附近就有几个.”而获得“蘑菇”的方法就是不断反思题目中的条件和结论,尝试提出新问题.深入思考本题的题干条件和解答过程,有以下几个反思:

反思1 将题干中的椭圆C换成任意椭圆(椭圆的中心在原点,且关于坐标轴对称,后面所说的任意椭圆都有这个限制),焦点F变为Q(t,0)(0,±a),其余条件不变,则直线DE的斜率与AB的斜率比值还是定值吗?

反思2 将题干中的椭圆C换成任意椭圆,焦点F变为Q(t,0)(0,±a),其余条件不变,则直线DE还过定点吗?

反思3 将题干中的椭圆C换成任意椭圆,直线AB所过定点为P(s,0),焦点F变为Q(t,0)(0,±a),其余条件不变,则直线DE的斜率与AB的斜率比值还是定值吗?

反思4 将题干中的椭圆C换成任意椭圆,直线AB所过定点为P(s,0),焦点F变为Q(t,0)(0,±a),其余条件不变,则直线DE还过定点吗?

反思5 命题者是以什么背景命制的本试题呢?

3 性质探究

解决问题时,除了正确地解决问题,更重要的是通过问题的解决提高能力,积累经验,拓展数学思维.而对试题进行一般化推广就是一种锻炼数学思维的重要途径.从前面的解题归纳总结中,我们获得了如下的一些性质.

性质1 如图2,已知椭圆C:=1(a >b >0),直线AB过原点O,Q(t,0)(0,±a)为x轴上的定点,过Q的直线AD与椭圆交于D,过Q的直线BE与椭圆交于E,记直线DE的斜率为k1,直线AB的斜率为

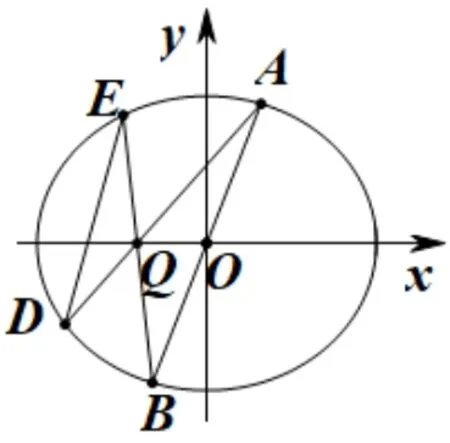
图2

将题干中的椭圆C推广为任意椭圆,将焦点F推广为任意一点Q(t,0)(0,±a),得到了性质1 和性质2.进一步一般化条件,可得到下面的性质3 和性质4.

性质3 如图3,已知椭圆=1(a >b >0),直线AB过定点P(s,0),且交椭圆于A,B两点,Q(t,0)(0,±a)为x轴上的定点,过Q的直线AD与椭圆交于D,过Q的直线BE与椭圆交于E,记直线DE的斜率为k1,直线AB的斜率为k2,则有

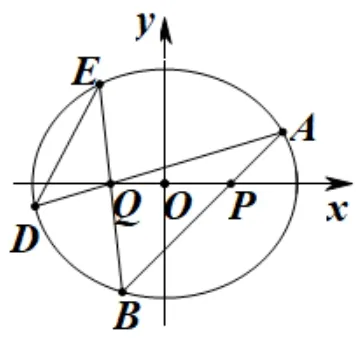
图3

将题干中的椭圆C推广为任意椭圆,将直线AB所过原点推广为任意一个定点P(s,0),将焦点F推广为任意一个定点Q(t,0)(0,±a),得到了性质3 和性质4.可以发现,运用解析法证明这些性质时,运算量非常地大.那么此题还能进一步推广吗? 答案是肯定的.

虽然前面我们将问题进行了初步推广,得到了几条性质.然而,到目前为止,我们还是没发现命题者命制本题的背景.为了更加清楚地揭示此题的背景,我们给出下面的定理1,并运用定理1 结合直线的参数方程证明定理2,最后用定理2再次证明性质2 和性质4.

4 背景溯源

图4

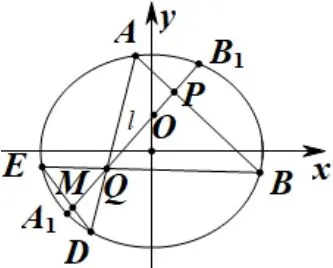
图5

由于P,Q为定点,故t4和t0是定值,而t1+t2与t1t2可由直线l的参数方程与椭圆的方程联立,再结合韦达定理求解而得出结果(特殊的可直接写出),且t1+t2与t1t2是定值,故t3也是定值,这说明M为定点,即直线DE过定点M.

下面,用定理2 来证明性质2 和性质4.

由此可见,命题者应是以定理1 作为背景来命制的这道试题,只不过是取了其中最特殊的一种情况,即定理1 和定理2 中的直线为直角坐标系中的轴.如果将一般的情形作为考试试题,那么不熟悉这个背景的学生将会面临很大的运算困难.事实上,从前面试题的解答来看,即使是特殊的情形,其运算量都已经相当大了.文献[1]中将定理1 称为二次曲线中的蝴蝶定理,其特殊情况为二次曲线中的坎迪定理[2].本文所证结论皆可以推广到双曲线和抛物线,感兴趣的读者可自行探究.

值得一说的是,解题是最能体现教师专业素质的一项活动,更是一项基本功.常言道:“教师教给学生一碗水,自己要有一桶水.”教师解题不能只停留在做出了答案,还得深挖试题背景,做到知其然,更要知其所以然.虽然未必要把所有的知识传授给学生,但是看清问题的本质本身也是一件令人赏心悦目的事.