星状河渠网络中非稳定流的精确边界能控性
2022-04-24于立新
史 琨,于立新
(烟台大学数学与信息科学学院, 山东 烟台 264005)
1 引言及预备知识
考虑如下一阶拟线性双曲型方程组
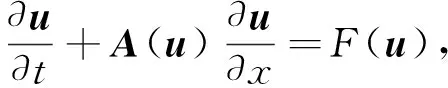
(1)
其中u=(u1,…,un)T是关于(t,x)的未知向量函数,A(u)是一个n×n的矩阵,并且带有光滑项aij(u) (i,j=1,…,n),且F(u)满足
F(0)=0。
(2)
由双曲型的定义, 在所考虑的区域上, 对任意给定的u,A(u)有n个实特征值λ1(u),…,λn(u), 满足
λr(u)<0<λs(u) (r=1,…,m;s=m+1,…,n),
(3)
且具有一组线性无关的左特征向量li(u)=(li1(u),…,lin(u))(i=1,…,n)即
li(u)A(u)=λi(u)li(u),det|lij(u)|≠0。
(4)
设vi=li(u)u,vi被称为第i个特征值所对应的对角变量。
给定边界条件
x=0:vs=Gs(t,v1,…,vm)+Hs(t)(s=m+1,…,n),
(5)
x=L:vr=Gr(t,vm+1,…,vn)+Hr(t)(r=1,…,m),
(6)
其中Gi和Hi(i=1,…,n)是关于其变量的适当光滑的函数,不失一般性,假设
Gi(t,0,…,0)≡0(i=1,…,n)。
(7)
给定初始条件
t=0:u=φ(x),0≤x≤L。
(8)
为了保证精确边界能控性,需要在区域R(T)={(t,x)|0≤t≤T,0≤x≤L}上有一个经典解,这里T>0可能是一个适当大的数。这种经典解被称为半整体经典解,它不同于整体经典解,也不同于局部经典解。为了后续的证明,引入如下两个引理。
引理1[2]假设lij,λi,fi,Gi,Hi(i,j=1,…,n)和φ关于其变量都是C1函数。进一步假设式(2)—(4)和(7)成立, 且在点(t,x)=(0,0)和(0,L)处分别满足C1相容性条件。 则对于任意给定T0>0, 混合初边值问题(1),(5),(6)和(8)在区域R(T0)={(t,x)|0≤t≤T0,0≤x≤L}上存在唯一的半整体C1解u=u(t,x),其C1模充分小,只要||φ||C1[0,L]和||H||C1[0,T0]足够的小(依赖于T0)。
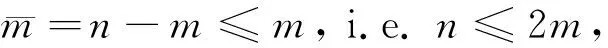
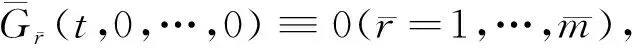
t=T:u=Φ(x), 0≤x≤L。
(9)
在实际生活中, 很多问题可以转化为数学中的拟线性双曲型方程问题,例如, 石油运输管道、河渠模型中的能控性问题。 最初, CIRIN[1-2]考虑了带有线性边界条件的拟线性双曲型方程组的精确边界能控性问题,之后, 文献[3-5]对具有一般非线性边界条件的一阶拟线性双曲型方程组的精确边界能控性建立了完备的理论。 基于此理论, 文献[6-8]实现了波动方程的精确边界能控。 同时, LI[5,9]和GU等[10]得到星状河渠网络的精确边界能控性结果。
在对于星状河渠网络中Saint-Venant方程组能控性研究的过程中, LI[5,9]对于n条河渠构成的星状河渠网络的能控性结果主要分为两种情况:其一, 实现了n个控制全部施加在简单结点处的能控性;其二, 受制于复结点处的边界条件, 实现了在复结点处施加一个控制, 其余n-1个控制施加在简单结点处的能控性。 文献[10]将LI[5]的第二种情况推广, 实现了在n条河渠构成的星状河渠网络中, 仅在n-1个简单结点处施加控制的能控性,而在实际应用中, 某些情况下全部简单结点或部分简单结点不可施加控制。本文首先改变原先在复结点处的边界条件, 使得边界条件更为一般化, 从而控制不再受限, 且改变后的边界条件仍可被等价改写为一般的非线性边界条件, 在下文第2部分有详细证明。 本文中, 首先得到了将n个控制全部施加在复结点的能控性结果。 其次, 对于文献[5]中的第二种能控性和文献[10]中的能控性, 本文分别将其推广, 在相同控制数量和控制时间的情况下, 施加在复结点与简单结点的控制数量可以任意分配, 依然可以实现河渠网络的能控。
本文安排如下: 第2部分得到关于具有一般边界条件的Saint-Venant方程组的半整体C1解的存在唯一性,第3部分给出了关于星状河渠网络仅在复结点处施加控制和在复结点与部分简单结点任意分配控制的精确边界能控性结果。
2 混合初边值问题的半整体C1解
考虑Saint-Venant方程组
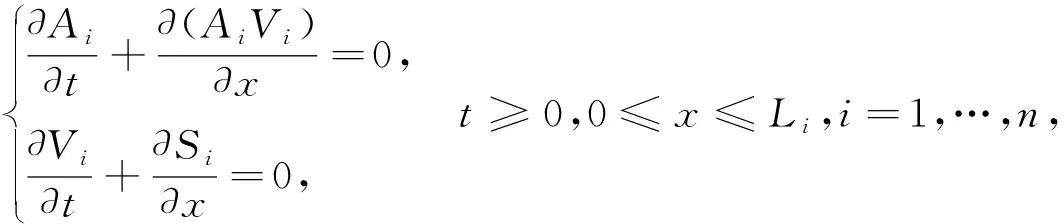
(10)
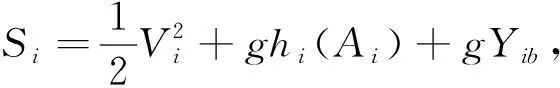
初始条件
t=0:(Ai,Vi)=(Ai0(x),Vi0(x)),0≤x≤Li,i=1,…,n,
(11)
当x=Li是简单结点时,给定边界条件
x=Li:AiVi=qi(t),
(12)
当x=0是复结点时,给定边界条件
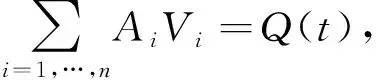
(13)
Sk=S1(k=2,…,m),
(14)
Aj=aj(t)(j=m+1,…,n)。
(15)
若
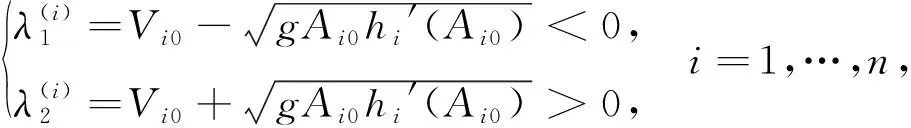
(16)
则称平衡状态(Ai,Vi)=(Ai0,Vi0)(i=1,…,n)是亚临界的。
在亚临界的平衡状态(Ai,Vi)=(Ai0,Vi0)(i=1,…,n)处, 边界条件(13)和(14)满足
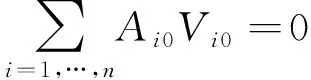
(17)
和
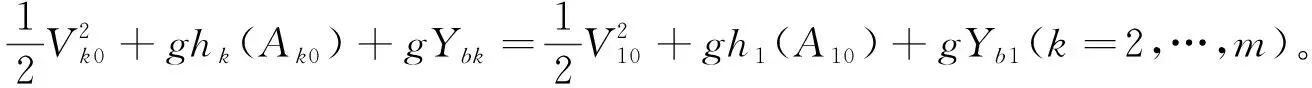
(18)
根据文献[3]中对于混合初边值问题的半整体C1解相关理论, 有如下定理:
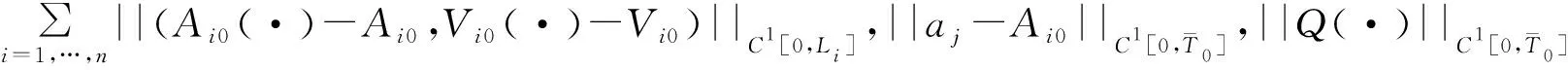
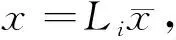
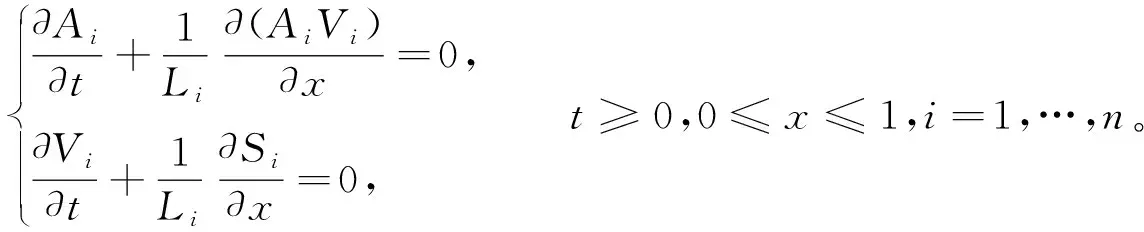
(19)
引入黎曼不变量ri和si, 其中
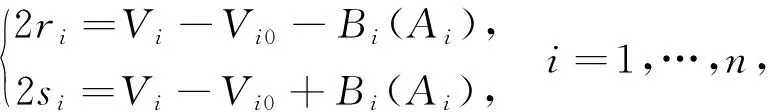
(20)
这里
由式(20), 可得到
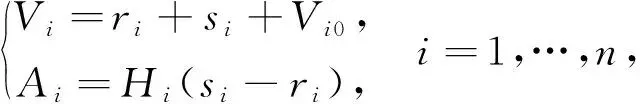
(21)
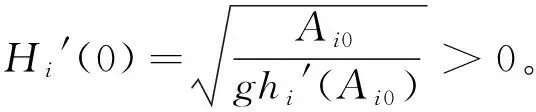
将(ri,si)(i=1,…,n)作为新的未知量, 则平衡态(Ai,Vi)=(Ai0,Vi0)等价于(ri,si)=(0,0), 方程组(19)能够被等价地改写为如下的对角形式
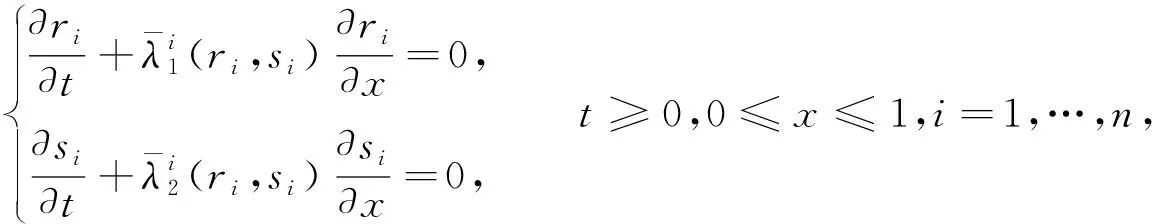
(22)
其中
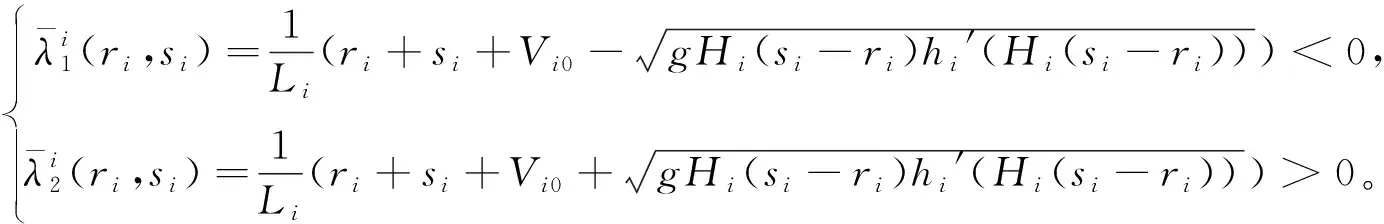
(23)
同时, 初始条件(11)可以被等价地改写为
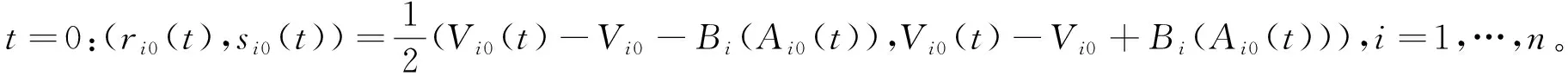
(24)
边界条件(12)能够被等价地改写为
x=1:Pi(t,ri,si)(ri+si+Vi0)Hi(si-ri)-q(t)=0,
(25)
计算易得
由隐函数存在性定理, 在(ri,si)=(0,0)(i=1,…,n)的某邻域内边界条件(25)能够被等价地改写为
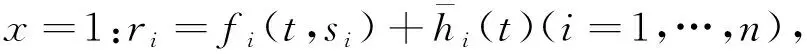
(26)
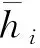
fi(t,0)≡0
(27)
和
(28)
由式(21), 在x=0处的边界条件(13)-(15)可以被等价地改写为
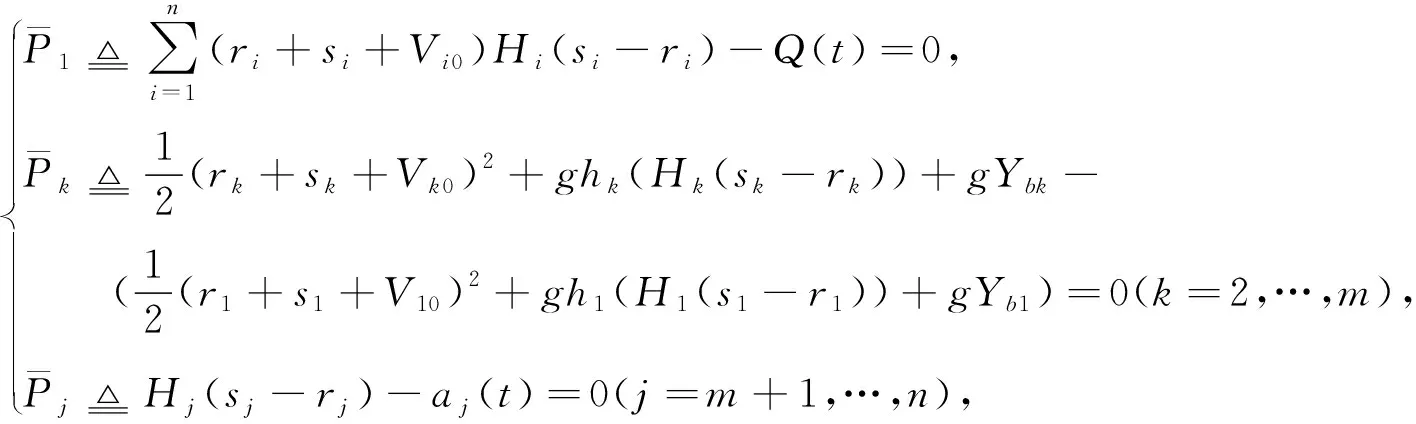
(29)
则有
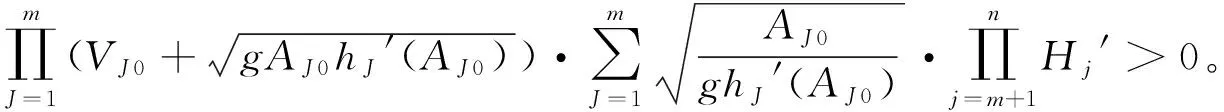
(30)
由隐函数存在性定理, 在(ri,si)=(0,0)(i=1,…,n)的某邻域内, 边界条件(29)能够被等价地改写为
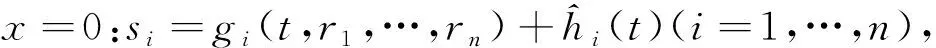
(31)
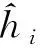
gi(t,0)≡0
(32)
和
(33)

注1 当m=n时, 在x=0处的边界条件(13)—(15)变为
Sk=S1(k=2,…,n)。
相应地,式(30)变为
注2 当m=1时, 在x=0处的边界条件(13)—(15)变为
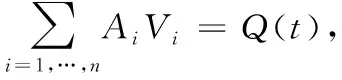
(34)
Aj=aj(t)(j=2,…,n)。
(35)
相应地,式(30)变为
3 星状河渠网络中不稳定流的精确边界能控性
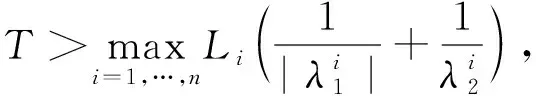
t=T:(Ai,Vi)=(AiT(t,x),ViT(t,x)),0≤x≤Li(i=1,…,n)。
(36)
证明由定理1的证明和注2, 在黎曼不变量下, 方程组(10), 初始条件(11)和边界条件(12)可被分别等价改写为式(22), (24)和(26)。
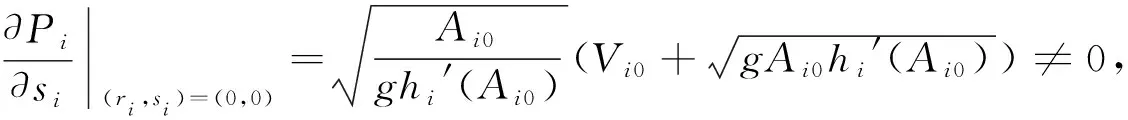
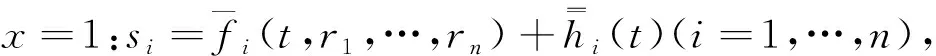
(37)
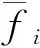
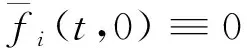
(38)
和
(39)
由式(21), 终端条件(36)可被等价地改写为
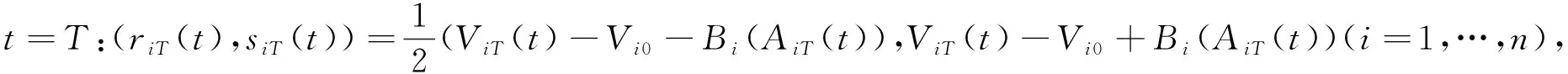
(40)
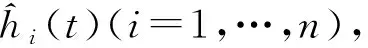
注3 LI在文献[5]中的定理7.6考虑了控制全部施加在简单结点的能控性。 在控制时间和数量不变的情况下, 本定理实现控制全部施加在复结点处的能控性。
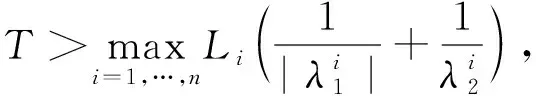
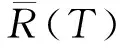
将解(r1,s1)=(r1(t,x),s1(x,t))代入式(29)中的第二式, 有
对于k=2,…,m,有
由隐函数的存在性定理, 在(rk,sk)=(0,0)(k=2,…,m)的某邻域内, 边界条件(14)能够被等价地改写为
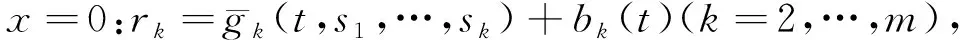
(41)
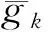
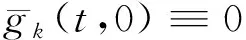
(42)
和
||bk||C1[0,T]<<0,
(43)
另一方面, 对于k=2,…,m,也可得到
由隐函数存在性定理, 在(rk,sk)=(0,0)(k=2,…,m)的某邻域内, 边界条件(14)能够被等价地改写为
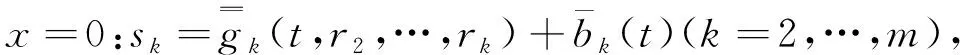
(44)
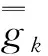
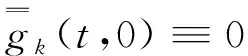
(45)
和
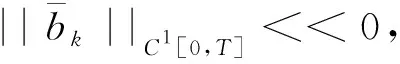
(46)
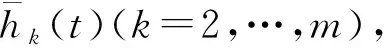
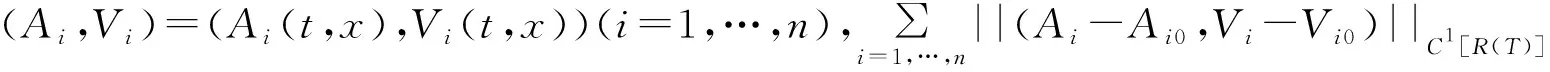
注4 在文献[5]中的定理7.7证明了当m=n时河渠网络的精确边界能控性。 定理3将其推广, 在控制时间与总量不变的前提下, 控制可以任意分配在复结点或者简单结点。
以上两个定理控制的数量都为n,而文献[10]在n-1个简单结点处施加控制, 实现由n条河渠构成的星状河渠网络的能控性。 下面我们在保证控制数量和时间不变的前提下, 证明了在简单结点与复结点任意分配n-1个控制亦可实现能控性。为后续定理的证明引入以下引理:
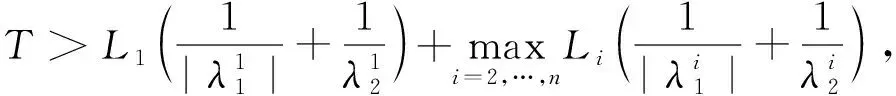
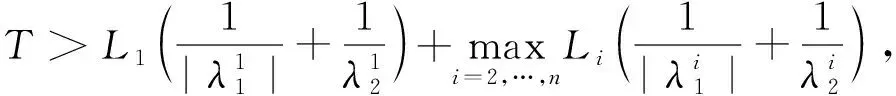
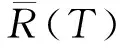
将解(Aj,Vj)=(Aj(t,x),Vj(t,x))(j=m+1,…,n)代入到边界条件(13), 有
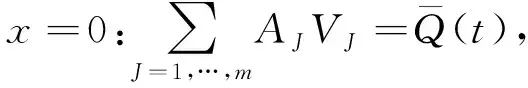
(47)
其中,