梳齿结构与振动梁复合的硅微谐振器的非线性分析

周春燕，胡博

（北京理工大学 宇航学院，北京 100081）

硅微谐振器通常作为传感器敏感元件，在MEMS中具有广泛应用. 硅微梁式谐振器以弹性梁作为敏感元件，通常采用梳齿电容进行动态扫频加载和频率检测[1]. 其原理是通过将被测物理量（压力、加速度、温度等）的改变转化为弹性梁轴向受力，从而改变梁的固有频率. 但随着MEMS 体积的减小，谐振器尺寸常在微米甚至纳米级别，系统与结构的力学特性表现出很强的尺度效应[2]，输出信号中的噪声干扰将越来越明显. KAAJAKARI 等[3]通过增大振动幅度的方式提高信噪比. 但是在微尺度下，振动幅度增大将使谐振梁的振动特性具有非线性，产生分岔不稳定性[4-6]. 机械非线性的产生，使得整个梁结构的幅频响应曲线右倾，弯曲到更高的频率，造成谐振器振幅受限，无法获得稳定振荡所需要的相位，造成大信噪比等不利影响[7-8]. 因此很有必要对谐振器结构的非线性展开研究分析，在设计中尽量增大振幅的同时避免非线性带来的负面影响.

YOUNIS 等[9]考察了两端固支的微机械谐振梁在平板电容激励下的非线性响应，讨论了不同振幅和阻尼条件下振动特性的理论解. SHAO 等[10]采用频闪扫描电子显微镜，实验观察了两端固支谐振梁，在中间连接分离式梳齿电容激励下的非线性响应.CHEN 等[11]研究了采用平板电容的反向静电力非线性，来降低微梁谐振器的非线性效应的方法，由于无法获得谐振梁的非线性解析方程，该方法只能采用盲试的方式进行. TSAIN 等[12]研究了环式谐振陀螺仪的两个变量耦合的非线性振动方程，并采用数值方法进行了非线性求解.

近年来，研究者们发现将梳齿结构直接加工在振动梁上的谐振器结构，可以获得更高的固有频率和灵敏度[13]. 对于特定尺寸下的梳齿结构与振动梁复合的硅微谐振器，刘梦霞等[14]通过有限元仿真分析，研究了不同振幅条件下非线性刚度与线性刚度的比例关系，并通过实验分析验证了有限元结果的正确性.

然而，为了进一步指导结构优化设计，需要从机理上分析这类谐振器的非线性行为给谐振器响应带来的影响，尤其是需要了解非线性响应与结构几何参数、激励电压、阻尼系数等的关系. 此外，准确理解非线性跳跃阶段后的结构动力学规律，也可以指导系统控制策略，以合理利用系统的强非线性段的高信噪比同时避免非线性带来的不确定现象. 本文将从力学分析入手，通过静力学和动力学理论推导，建立梳齿结构与振动梁复合的硅微谐振器的动力学方程. 并对方程进行理论分析和数值验证，最后通过实验数据验证理论结果的正确性.

1 原理及分析

1.1 工作原理

如图1 所示，以谐振式加速度计为例，整个结构通过锚点固定，主要由与折叠梁相连的检测质量块、双端固支音叉式谐振器、微杠杆以及支撑结构组成.

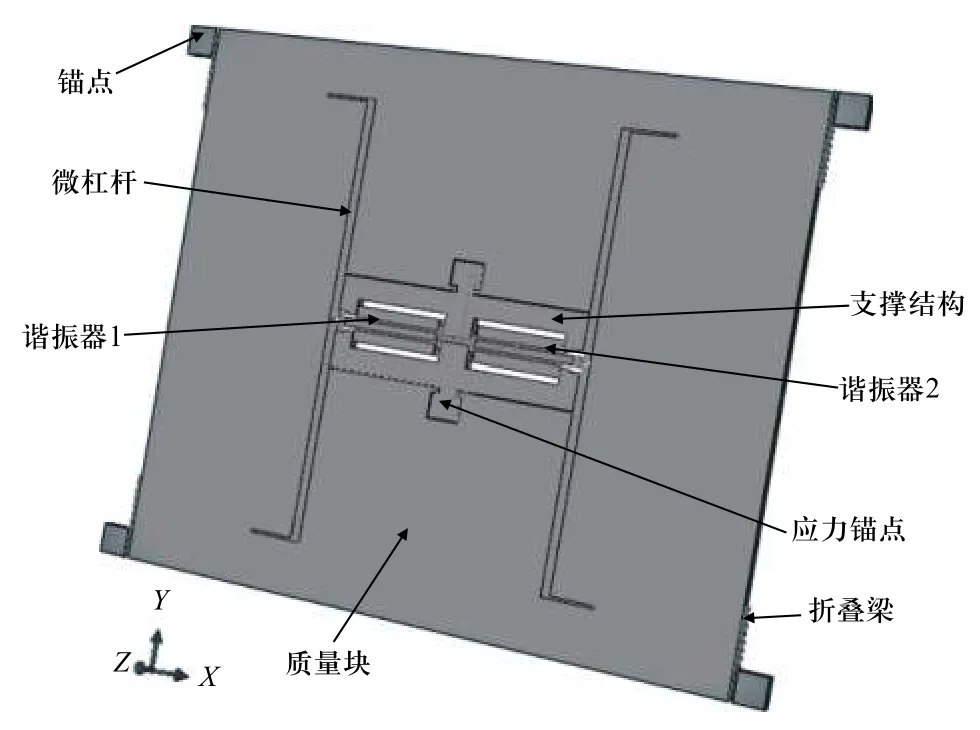
图1 谐振式加速度计示意图Fig. 1 Schematic diagram of resonant accelerometer

当谐振器工作时，电容使得左右谐振梁保持在其本征频率上. 当在检测方向上受到加速度的作用时，质量块发生横向移动，在微杠杆结构的作用下，使得左右两边的梁结构分别受到轴向的拉力和压力，从而使其频率一端增大，另一端减小，根据频率差推导求出待测加速度大小. 图2 为梳齿结构与振动梁复合的硅微谐振器的结构示意图，滑膜梳齿结构作为驱动电容和检测电容. 因为驱动电容与振幅的二阶导数等于0，所以静电刚度为0，在分析结构非线性时仅需考虑机械非线性的影响[14].

图2 梳齿结构与振动梁复合的硅微谐振器的结构示意图Fig. 2 Schematic diagram of silicon microresonator with vibrating beam integrated with comb fingers structure

1.2 动力学方程推导

如图3 所示，对梳齿结构与振动梁复合的硅微谐振器进行力学分析. 谐振器在振动时两端固定，左半梳齿电容上施加驱动力，右半梳齿电容进行检测.考虑到整根梁上梳齿的分布较为均匀，可以近似认为梁的左半部分受均布载荷的作用. 结构的受力情况简图如图3 表示，梁的长度为L，厚度为h，其中虚线部分为变形后的示意图.

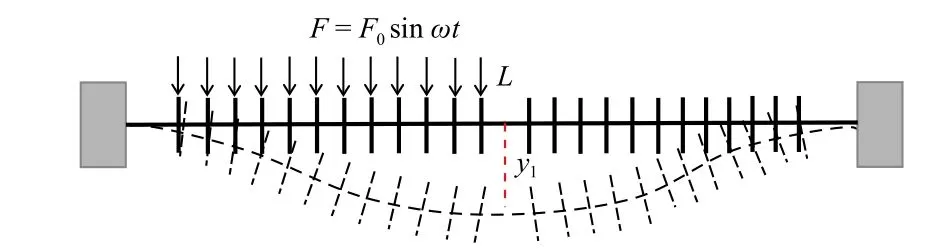
图3 结构受力示意图Fig. 3 Schematic diagram of structural forces

考虑到中心梁的长厚比通常大于10，可以采用欧拉-伯努利梁模型对结构进行分析.假设梁的各截面的中心主惯性轴在同一平面XOY内，外载荷也作用在该平面内，梁在该平面内做横向振动，这时梁的主要变形是弯曲变形.

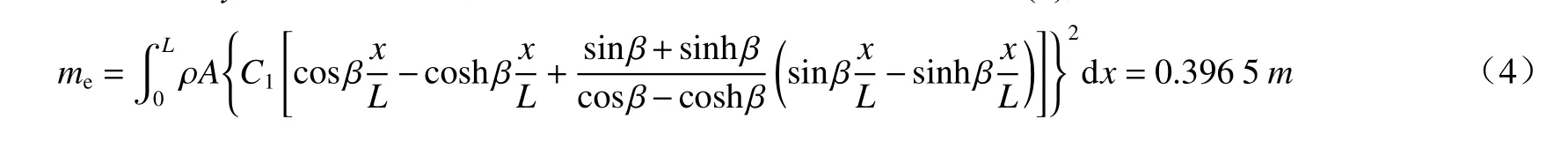
品质因数（Q值）是研究谐振器的一项重要参数，通过半功率带宽法可以对其进行求解. 考虑到该方法已经普及[17-19]，因此本文将同样使用该方法，通过多组实验测得的扫频数据求得阻尼比.

式（15）为梳齿结构与振动梁复合的硅微谐振器的一般动力学方程，可以看到结构具有广义位移的三次非线性关系. 对于不同尺寸参数的谐振器，只需要将对应数据代入公式，即可快速得到它的各项参数求解，实现了从理论上研究结构机械非线性的目的. 从刚度非线性的结果分析，可以发现给定位移（输出信号）条件下，结构的非线性力与中心梁的面积成正比. 考虑到MEMS 梁通常为矩形结构，因此非线性力与线性力的比值与梁的厚度的平方成反比，即梁越薄非线性效应越强.

为了进一步分析非线性刚度对于硅微谐振器的动态特性的影响，下面对结构进行动力学方程进行分析. 首先对方程进行量纲一化变换，令

在平均化时，与 Φ相比，Y和 φ随时间t的变化要慢得多.即在振动周期2π/ω0中，Y和 φ几乎不发生变化，这就可以在式（23）和（24）中对 Φ的变化取平均.因此，对这两个方程在周期2π/ω0内取平均，并在实行平均化时将Y、 φ、Y˙ 和 φ˙考虑作为常数，这样可以得到如下的描述Y和φ缓慢变化的方程

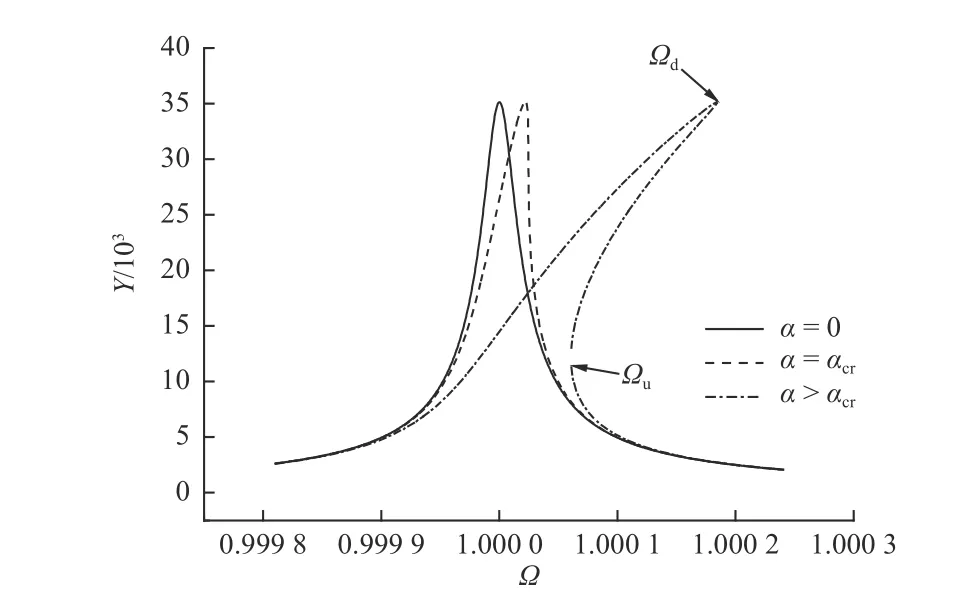
图4 不同α 下的幅频特性曲线Fig. 4 Amplitude-frequency characteristic curve under different α

1.3 实验验证

为了使验证理论分析结果，针对图2 所示的谐振器进行了扫频实验. 表1 为实验所用谐振器的基本参数，实验选取了激励电压从0.41～5.01 mV 的多组数据进行处理.

表1 谐振器尺寸参数Tab. 1 Resonator size parameters

为了验证理论曲线的合理性，利用Runge-Kutta法对方程（33）进行正向、反向扫频分析，得到该结构梁在不同输入电压时的量纲一幅频响应曲线，然后进行物理量分析，得到系统的幅频曲线数值解. 如图5 所示，由于非线性失稳，在 3.01 mV 激励下，正向扫频时在频率峰值( Ωd)处，系统振幅发生下跃；反向扫频时在 Ωu附近会发生振幅上跃. 谐振梁的振动微分方程扫频法求得的数值解与平均法求得的理论解具有极高的一致性，从而说明了平均法在求解该问题时具有一定的适用性，同时也说明了非线性理论振动分析的正确性.

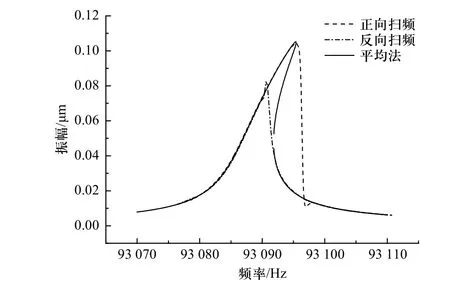
图5 驱动电压为3.01 mV 时的扫频曲线和平均法数值解曲线Fig. 5 Sweep frequency curve and averaging method numerical solution curve when the driving voltage is 3.01 mV

接下来，在不同输入电压的情况下，将平均法求得的幅频曲线理论解与实验数据进行比对. 如图6所示，沿着纵坐标方向由下往上，激励电压逐渐增大.其中实线为理论的数值解，虚线为实验反向扫频测得的数据.

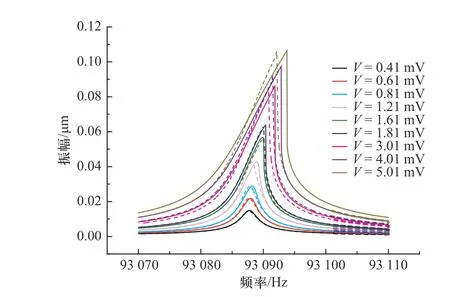
图6 不同电压下的幅频曲线Fig. 6 Amplitude-frequency curve under different voltage

由图6 可以看出，1.61 mV 接近系统发生跳跃的临界电压.当输入电压小于1.61 mV 时，幅频响应曲线不发生跳跃，理论曲线与实验数据几乎可以吻合；当电压继续增加时，谐振梁的频率发生偏移，进入非线性状态，且随着驱动电压的增加，幅频曲线向右偏移的幅度也不断增加，频率跳跃现象逐渐明显.式（32）给出的系统发生跳跃失稳的临界峰值振幅为0.054 μm，实际测量得到1.6 mV 振幅峰值为0.056 μm，误差为3.7%.

考虑到在实际工况中，对于两个对称的谐振梁，当其处于非线性的状态时，上下两根梁模态并不相同，产生的位移也并不对称. 而理论推导将其近似为对称变形，因此在结果上可能产生一点的误差，使得出现图6 中实验与理论结果的偏移情况.

由于系统反向扫频的实验曲线通常比较稳定，不容易受扫频参数的影响，因此也可以利用反向扫频得到的峰值频率进行系统设计. 对于图1 所示的差分结构，如果两端谐振器具有相同的幅频特性，那么发生非线性失稳后的频率差仍然能反映测量加速度的变化.

在对实验数据整理的过程中，发现在临界电压1.54 mV 附近时频率峰值会出现跳跃的现象，如图7点状图所示. 前面的理论研究表明，在小于临界电压时，测试得到的固有频率为峰值频率（黑色方型散点），即式（30a）表示的下跃频率；超过临界电压后，由于动力学失稳，测试得到的频率（黑色圆形散点）为式（30b）上跃频率. 为了验证理论结果，将式（30a）与（30b）所表达的理论曲线与试验结果比较如图7所示.

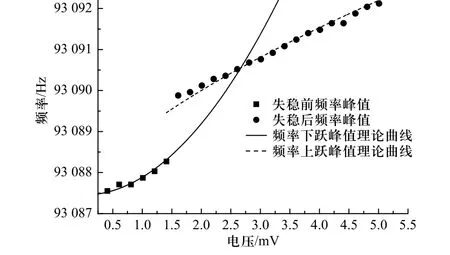
图7 输入电压-频率关系拟合曲线Fig. 7 Fitting curve of input voltage-frequency relationship

由图7 可以看出，即使是结构处在稳定状态，结构的固有频率随着激励幅值的增加而上升，因此在设计器件时需要精确控制结构的振幅，才能得到准确的固有频率. 此外，从实验结果看，当激励电压从1.4 mV 上升到1.6 V 后，频率发生了明显跳跃的现象.为了从理论上分析这一奇特现象，对临界激励条件下的结构上跃频率和下跃频率进行详细分析.联立方程（30a）、（30b）和方程（32）可得，在临界条件下

2 结 论

本文针对梳齿结构与振动梁复合的硅微谐振器，进行了非线性动力学分析. 首先采用能量法建立了结构的非线性动力学方程，然后采用平均化方法对方程进行了理论求解. 利用Runge-Kutta 数值积分法对振动微分方程的扫频求解以及平均法求得的理论解进行比对，结果较好地吻合说明了平均化方法对求解该问题的及适用性. 然后，通过不同激励电压下解析解的曲线与实验曲线对比，验证了理论分析的准确性.

理论分析表明：①结构的机械非线性刚度，主要受谐振梁的厚度影响，与梳齿的数量、间距、厚度等无关；②在结构发生非线性失稳的临界状态，理论和实验表明的固有频率会发生跳跃，这个现象会给差分式谐振传感器带来较大的误差；③结构发生失稳前的最大振幅与梁的厚度以及阻尼比的1/2 次方成正比，因此，适当中心梁的厚度或增加结构阻尼能有效增大系统稳定响应的位移和输出电压信号；④发生失稳的上跃频率更容易测量，且非线性误差相对于峰值频率要小很多，因此采用上跃频率设计器件能得到更高的精度和更高的信噪比.

相比以往在仿真和实验过程中逐个调整参数大小以观察谐振器非线性特性，而实际工况无法满足低压激励等弊端，该理论推导提供了一个普遍适用的参考，仅需将不同的参数代入公式，即可求解出该结构不同尺寸在使用时的力-位移曲线、幅频曲线、固有频率以及阈值电压，进而研究非线性效应，既可以有效避免谐振器在非线性的状态下工作，又极大地简化了研究过程，降低了仿真和实验带来的成本.这项工作也对接下来研究三自由度差分型谐振器在实际使用时振动串扰的研究、非线性效应的优化提供了基础.