破片式战斗部对预警机毁伤评估研究

张睿文，裴扬，侯鹏，葛玉雪

（1. 西北工业大学 航空学院, 陕西，西安 710072；2. 西安航天动力研究所 液体火箭发动机技术重点实验室，陕西，西安 710100；3. 航空工业光电所 光电控制技术重点实验室, 河南，洛阳 471023）

预警机能够在复杂的战场环境下监视、跟踪和识别目标，向各作战单元分发情报，指挥引导飞机和导弹执行攻击任务，是现代空中战场的管理中心，也是作战体系的核心和枢纽节点[1-2]. 预警机的重要性使其成为体系作战的首要攻击目标，导弹对预警机的毁伤效果也成为体系作战的重要问题.

用于攻击预警机的地空或空空导弹通常采用破片式战斗部. 已有文献研究了破片式战斗部对攻击机[3]、战斗机[4]、武装直升机[5]、运输机[6]等多种类型飞机的毁伤评估问题，建立了这些飞机气动[7]、结构[8-9]、飞控[5]、燃油[10]、动力[5]、液压[5]等系统的易损性模型. 除上述典型系统外，预警机还包含雷达、敌我识别、电子侦察、通信、导航和指挥控制等任务系统[11]，这些系统是执行任务的重要保障，也是易损性建模和毁伤评估的关键要素. 熊森才等[12]研究了相控阵雷达天线的毁伤机理和判据. 郭淼等[13]研究了破片和冲击波对雷达天线罩的复合毁伤模型. 李超等[14]研究了破片式战斗部对地面雷达系统的毁伤评估问题，构建了雷达系统的毁伤树模型. 陶灵姣等[15]研究了地面机动指挥系统的毁伤模型. 上述研究了雷达、指挥控制等关键系统的毁伤机理，但尚未研究包含这些系统的预警机整体的易损性模型. 赵宏伟等[16]在杀爆弹打击预警机的引战配合研究中建立了预警机的易损性模型，但其模型经过了较多的简化，缺少各系统的毁伤模型.

在飞机易损性模型基础上，结合战斗部威力场模型和弹目交会条件，可以分析战斗部对飞机的毁伤效果. 梁斌等[10]研究了不同脱靶量、交会参数和爆炸点距离下离散杆和EFP 组合战斗部对飞机的毁伤效果. 司凯等[4]研究了破片式战斗部在飞机顶部、侧向等不同位置对飞机的毁伤效果. KONOKMAN等[17]研究了典型攻击方向下破片式战斗部对飞机的毁伤效果. 上述研究大多在给定的爆炸点计算毁伤概率. 破片式战斗部通常采用近炸引信，爆炸点与引信探测起爆的动态过程密切相关. ZHAO 等[18]建立了激光近炸引信的探测起爆过程模型，分析了战斗部的最佳起爆时间. 张合等[19]研究了周视激光引信的探测起爆过程，分析了最佳起爆时间和起爆角的影响因素. 吉阳等[20]研究了相控阵引信的扫描探测过程和起爆控制优化问题. 但上述文献未能考虑目标系统层面的毁伤特性，且忽略了目标实际外形对起爆计算的影响.

针对上述问题，本文对预警机的易损性建模以及考虑引信探测起爆过程的毁伤评估问题开展研究.构建了典型预警机的易损性模型，在以往飞机易损性模型的基础上，根据预警机任务系统的特点，进一步建立任务系统的毁伤树模型. 然后，构建近炸引信探测起爆模型，采用扫描线法计算引信探测到目标的位置，并给出相对速度坐标系下、考虑目标外形的起爆延迟计算方法. 最后，采用蒙特卡洛方法计算毁伤概率，通过仿真算例分析交会条件、起爆延迟、制导精度和瞄准中心等因素对毁伤效果的影响.

1 预警机易损性模型

本文以采用涡桨发动机、起飞质量约25 t、载5名乘员的典型中型预警机为研究对象. 飞机毁伤分为KK、K、A、B 和C 5 个等级[21]，本文主要研究KK、B和C 级毁伤. 易损性模型包含致命性部件分析、几何模型、部件属性与毁伤准则、毁伤树模型等[22].

1.1 致命性部件分析

预警机由载机和任务系统两大部分组成，部件分为外形、结构和系统三类. 预警机以运输机作为载机平台. 常规运输机的外形部件主要有机身、机翼、平尾、发动机舱等. 结构部件主要有机身的梁、框，机翼和尾翼的梁、肋，发动机悬挂支架等. 载机系统主要包含飞行控制、电力、液压、燃油、动力、环控、起落架等子系统.

在常规运输机部件的基础上，预警机的外形部件还有雷达罩，且机身分为机头舱段、设备舱段、任务舱段和机尾舱段4 个舱段. 结构部件还包括雷达罩的横、纵梁和支架. 载机系统中的环控系统还包括支持电子设备工作的蒸汽循环系统和散热器. 除载机系统部件外，预警机还包含任务系统部件，进一步分为若干分系统. 雷达、敌我识别、通信、电子侦察和导航系统均由天线和信息处理设备两部分组成.雷达天线和敌我识别天线均在雷达罩内；电子侦察天线位于机头、机尾和左右机翼；HF、UHF、VHF/UHF 3 组频段的通信天线位于机身、机翼等处；全球定位系统（global positioning system，GPS）、雷达测高、战术空中导航系统（tactical air control and navigation，TACAN）和自动定向机（automatic direction finder，ADF）等不同功能的导航天线位于机身、雷达罩外等处. 将雷达系统的信息处理设备简化为收发设备和信号处理设备两个部件，敌我识别、通信、电子侦察和导航系统的信息处理各自简化为一个部件. 指挥控制系统由雷达指挥官、作战情报中心指挥官和空中管制指挥官3 名任务员，3 名任务员对应的工作站，以及两台任务计算机组成. 此外，还有雷达旋转轴、电机、传动箱等雷达系统的支持部件.

预警机的气动布局和飞行控制系统通常有较高的稳定性，翼面受到一定程度损伤后仍能飞行返航.机身桁梁、翼梁等主要结构部件也有较高的抗毁伤能力，少量破片的打击难以造成致命毁伤. 目前文献对此类飞机毁伤的研究主要考虑系统部件的毁伤，将外形和结构部件作为非致命性部件，仅考虑它们对其他致命性部件的遮挡作用[3-4,10].

1.2 几何模型

将机身、机翼、雷达罩等舱段的梁、肋模型简化为平板，供油管路和操纵系统的传动线路模型简化为空心管，其他设备模型简化为壳体. 任务系统中，雷达天线为八木天线，简化为空心管；其余系统天线简化为平板；计算机、操作台以及信息处理设备简化为壳体. 预警机及其部件的三维模型如图1 所示，其中图1(b)进一步区分了任务系统中各子系统的模型.

图1 预警机三维模型Fig. 1 3D model of early-warming aircraft

将三维模型离散化，用四边形面元拼接成各部件，建立预警机外形、结构和系统的面元模型，用于引信探测和战斗部毁伤计算，如图2 所示.

图2 预警机面元模型Fig. 2 Surface element model of early-warming aircraft

1.3 部件属性与毁伤准则

翼梁、机身桁梁等重要结构部件材料等效为钛合金，发动机部件、液压作动器、操纵系统线路、供油管路等部件材料等效为均质钢，其他部件材料等效为铝合金. 参考典型运输机的部件参数，翼面、机身舱段等外形部件等效厚度为2.0～3.5 mm；翼梁、机身桁梁等重要结构部件等效厚度为4～7 mm，其他结构部件等效厚度为3 mm；发动机部件等效厚度5～10 mm；油箱等效厚度10 mm；操纵线路等效直径4～6 mm；载机系统和任务系统部件厚度2～3 mm；预警雷达天线等效直径10～16 mm，其他天线阵元等效厚度2 mm[11,23]. 导弹战斗部对部件的毁伤包括冲击波毁伤和破片毁伤，本文主要考虑破片毁伤.

油箱毁伤采用引燃准则判定，破片对易燃类部件的引燃概率pi为[24]

式中：Sa为威胁与靶板的期望接触面积；ka为威胁形状系数；h为面元击穿情况下的侵彻厚度；θfrg为破片的打击方向与面元法线的夹角；δ为面元实际厚度.

任务系统中，雷达和敌我识别天线的面积较大，其毁伤采用面积消去准则判定. 文献研究表明，对于平面阵列天线，当超过50%的阵元失效时，天线将失效[12,25]. 目前缺少八木天线的毁伤准则研究，采用面积消去准则近似，即天线受损面积超过50%则失效.其他系统的天线面积较小，其毁伤采用穿透准则判定.

1.4 毁伤树模型

根据预警机的功能建立毁伤树模型. 以任务级毁伤为例，毁伤树如图3 所示. 在任务级毁伤下，根据不同功能的毁伤，进一步分为升力毁伤、动力毁伤、结构完整性毁伤、稳定性/操纵性毁伤和任务功能毁伤等分支. 与部件毁伤准则中的考量类似，忽略升力和结构完整性毁伤，仅考虑动力、稳定性/操纵性和任务功能毁伤. 各功能毁伤再细分出相关部件的毁伤. 各功能毁伤之间、每个功能毁伤下的部件毁伤之间为或门逻辑：任一功能毁伤，即无法执行任务；任一部件毁伤，即导致相关功能毁伤.

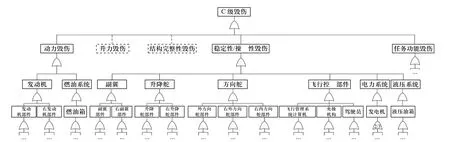
图3 任务级毁伤树Fig. 3 Mission level kill tree

对于任务功能毁伤，根据预警机任务系统的组成，进一步细分出各任务系统的毁伤，如图4 所示.其中，天线或信息处理设备二者之一的毁伤，都导致该系统的毁伤. 对于有多组天线的系统，多数天线毁伤即导致天线分系统的毁伤. 电子侦察系统至少需要3 副天线工作，以测定信号源的方位. 预警机执行任务需要3 个任务乘员及其设备的协作，其中之一毁伤则导致指挥控制系统毁伤. 两台任务计算机互为备份，同时毁伤则指挥控制系统无法正常运行.

图4 任务功能毁伤树Fig. 4 Mission function kill tree

B 级和KK 级毁伤树的构建方法与此类似. B 级毁伤树进一步分为安全性毁伤、动力毁伤和稳定性/操纵性毁伤，其中安全性毁伤采用引燃准则判定机翼油箱毁伤. KK 级毁伤树进一步分为安全性毁伤和动力毁伤.

2 战斗部威力场模型

与预警机的尺寸相比，战斗部的尺寸相对较小，假设战斗部沿中心轴对称，采用预制破片，所有破片均由一点飞散. 设破片数为nfrg，单枚破片质量为mfrg，破片初速为vfrg0，破片静态飞散角为Ω，破片静态飞散方位角为Φ. 如图5 所示，假设破片沿周向均匀分布，沿轴向在静态飞散区[Φ-Ω/2,Φ+Ω/2]内近似服从正态分布，均值为Φ，标准差按飞散区内包含90%以上破片估算，约为σΦ=Ω/6. 破片在空中运动时的速度衰减公式见文献[24].

图5 战斗部威力场示意图Fig. 5 Diagram of warhead power field

3 引信探测起爆模型

当导弹与目标进入交会终端时，引信开机探测目标. 探测到目标并积累足够强度的信号后，为提高毁伤概率，延迟一定时间，在最佳位置起爆. 引信探测起爆模型即在给定的交会条件和制导误差下，计算实际起爆的位置.

3.1 弹目交会与制导误差参数定义

设交会终端飞机和导弹分别以速度VA和VM匀速直线运动. 忽略导弹滚转角的影响，则弹目交会条件可用交会角Γ和交会方位角Λ 2个参数描述. 如图6 所示，交会角Γ定义为导弹速度反向矢量-VM与VA的夹角；交会方位角Λ定义为目标速度坐标系OXavYavZav中-VM在OYavZav面的投影与OYav轴的夹角，以绕OXav轴右手定则旋转方向为正.

图6 弹目交会参数定义Fig. 6 Definition of missile-target intercept parameters

导弹相对于飞机的速度为VR=VM-VA，定义以目标瞄准中心为原心的相对速度坐标系OXrYrZr，OXr轴与VR同向，OYr轴位于目标对称面内、垂直于OXr向上，OZr轴垂直于OXrYr平面向右，如图7 所示.OYrZr平面为脱靶平面，战斗部在OXr轴的坐标为径向距离. 设VR所在直线Lr与脱靶平面的交点为MH=(yMr,zMr)，脱靶距离ρ为O点与MH点的距离，脱靶方位φ定义为OMH与OYr轴的夹角，以绕OXr轴按右手定则旋转方向为正.

图7 制导误差参数定义Fig. 7 Definition of guidance error parameters

3.2 基于扫描线的引信探测计算方法

假设引信波束为锥体，波束宽度λ和引信作用距离Rfz均为定值. 如图8 所示，定义引信探测坐标系OXfYfZf，坐标轴平行于导弹机体坐标系的对应坐标轴，原点为引信中心. 定义波束中心OF与OXf轴的夹角为波束倾角η，最大波束倾角为ηmax. 从而引信的最大探测范围简化为半顶角等于ηmax+λ/2 的锥体包络.

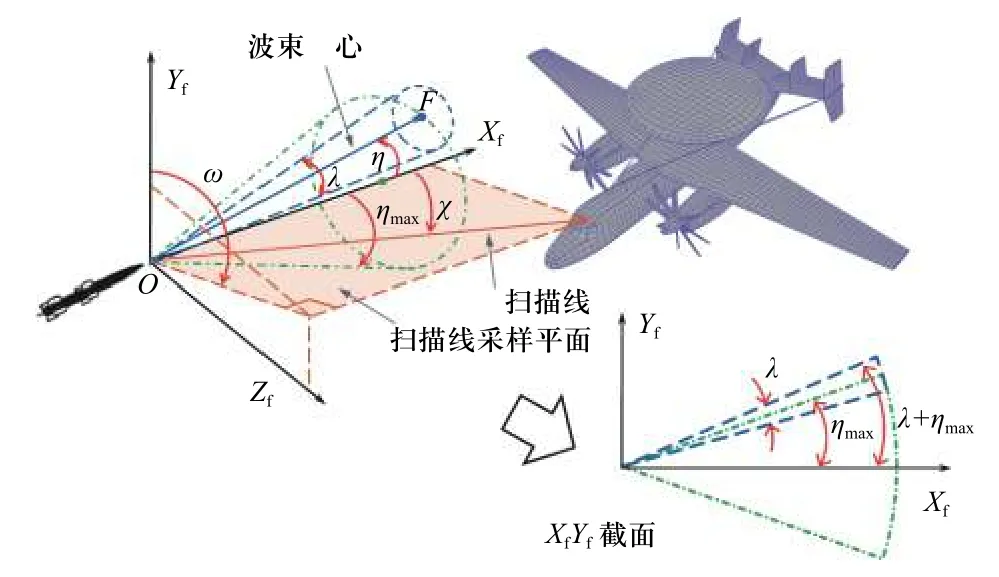
图8 引信探测示意图Fig. 8 Diagram of fuse detection

扫描线是为以引信中心为起点的射线. 定义扫描线与OXf轴的夹角为扫描线倾角χ，扫描线在OYfZf平面的投影与OYf轴的夹角为扫描线旋转角ω.给定目标与引信位置，在半顶角为ηmax+λ/2 的探测包络锥内，首先按照间隔Δω生成2π/Δω个经过OXf轴、垂直于OYfZf平面的采样截面. 然后，在每个采样截面内，按照间隔Δχ再生成(ηmax+λ/2)/Δχ个扫描线. 外加沿OXf轴的探测线，扫描线的总数nsl为

假设面元能够完整反射探测信号. 对每一条扫描线，遍历计算目标各个外形面元是否被探测线穿过；若任一面元被穿过，且交点距引信中心的距离小于引信作用距离Rfz，则认为在该位置下引信能够探测到目标.

根据面元的方向向量和其中一个节点的坐标，构建面元所在平面的点法式方程；根据扫描线的方向向量，构建扫描线的参数方程；联立这两个方程，解出扫描线与面元所在平面交点C的坐标. 根据余弦定理计算C点与面元各节点的夹角，若夹角之和等于2π，则C点在面元内，即扫描线与面元相交，C点为二者交点.

弹目交会时，在相对速度坐标系下，导弹沿直线Lr、自OXr负向朝正向运动. 给定弹目交会和制导误差参数，即可构建相对速度坐标系和战斗部运动线Lr. 采用固定步长采样的方法计算引信探测到目标的位置（简称探测位置）. 设定一个径向距离的计算区间[xMrd_min,xMrd_max]，径向距离xMr从xMrd_min开始，逐次增加ε，判断引信是否探测到目标：若是，则此径向距离为引信探测位置的径向距离xMrd，通过坐标变换得到此时导弹和目标在地面坐标系位置；否则再增加ε，继续判断；若增加到xMrd_max仍未探测到目标，则在此交会条件和制导误差下无法起爆.

3.3 自适应延迟起爆计算方法

最佳起爆点的准则是，当战斗部在该位置起爆时，目标瞄准中心落在破片飞散区的中心. 图9 为导弹和目标在相对坐标系中由OXr轴和MH点形成的平面上的运动分析. 在相对坐标系下，目标静止，导弹沿直线Lr向OXr轴正向运动. 静态飞散区域中心的破片速度矢量为Vfrg_s，其大小等于vfrg，与OXr轴正向的夹角为Φ. 相对速度坐标系下动态飞散区域中心的破片速度矢量是Vfrg_d与相对速度矢量之和，即：

图9 自适应起爆延迟示意图Fig. 9 Diagram of self-adaptive detonation delays

以往引战配合计算将目标简化为一个质点，但近炸引信通常在战斗部碰撞目标之前起爆，通过上述方法计算得到的起爆位置可能在战斗部触碰目标之后，需考虑目标的外形予以修正. 类似地，采用扫描线法计算战斗部触碰目标时的位置. 在计算得到引信探测位置的径向距离xMrd后，生成一个沿OXf轴，即倾角χ=0°、旋转角ω=0°的扫描线，然后计算与目标外形交点的距离dcld，则碰撞位置的径向距离xMrc=xMrd+dcld. 引信探测位置的径向距离为xMrd，设经过信号积累延迟tdf后径向距离为xMrs. 引信起爆位置的径向距离应在[xMrs,xMrc]区间内. 若计算得到的xMrb在区间外，则予以修正. 引信最佳起爆延迟为：

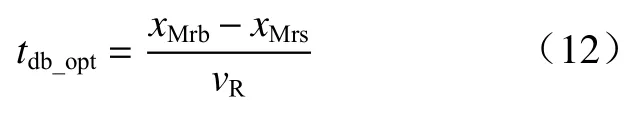
4 毁伤概率计算方法

采用蒙特卡洛方法计算给定交会条件和制导精度下的平均毁伤概率. 导弹的制导精度用圆概率误差（circular error probable，CEP）描述，定义为脱靶平面上，以目标瞄准中心为圆心，MH点落入圆内的概率为50%的圆半径. 毁伤概率计算的流程如图10 所示. 计算的初始条件是预警机在地面坐标系下的位置分量(xAg,yAg,zAg)、速度vA、偏航角ψA、俯仰角φA、滚转角φa、迎角αA和侧滑角βA，导弹的速度vM、迎角αM、侧滑角βM，弹目交会角Γ、交会方位角Λ，导弹制导精度CEP，以及预警机的易损性模型.

图10 平均毁伤概率计算流程Fig. 10 Calculation process of average kill probability

首先计算导弹相对于预警机的速度，然后将预警机易损性模型的节点坐标变换至相对速度坐标系.根据预警机的尺寸，设置引信探测起爆计算中径向距离的计算区间[xMrd_min,xMrd_max]；根据计算的精度需求，设置蒙特卡洛模拟的爆炸点样本数Nbp和引信探测起爆计算的步长ε. 假设MH点在脱靶平面y、z方向分别服从正态分布yMr～N(μH_y,σH_y)，zMr～N(μH_z,σH_z)，且μH_y=μH_z=0，σH_y=σH_z=σH，则MH点与目标瞄准中心的距离服从瑞利分布，CEP≈1.774σH[26]. 按概率分布生成MH的第i个样本点(yMr_i,zMr_i)，i=1,2,···,Nbp. 径向距离的样本点从xMrd_min开始，则第j个样本点为xMrd_j=xMrd_min+jε. 在(xMrd_j,yMr_i,zMr_i)处进行引信探测计算，判断是否探测到目标. 若探测到目标，则进一步计算起爆延迟和爆炸点的径向距离xMrb_j，转换至地面坐标系后，根据易损性模型和战斗部威力场计算毁伤概率. 若未探测到目标，则径向距离增加一个步长ε，在下一个样本点上继续进行引信探测计算. 若径向距离增大至xMrd_max仍未探测到目标，则该MH样本点的毁伤概率Pk=0. 完成第i个MH样本点的毁伤概率计算后，继续下一个样本点，直至计算完所有Nbp个样本点的毁伤概率，然后将这Nbp个样本点毁伤概率的均值作为给定交会角Γ、交会方位角Λ和制导精度CEP 下的平均毁伤概率Pk.

单个爆炸点的毁伤概率计算方法如下. 单枚破片打击下的毁伤概率采用射击线法计算[27]. 根据破片威力场，按照单枚破片的飞散方位生成射击线. 根据射击线和飞机面元模型，计算射击线穿过的部件.按照无余度无重叠、无余度有重叠、有余度无重叠和有余度有重叠4 种模型计算射击线的毁伤概率，部件之间的余度根据毁伤树模型判断，单个部件的毁伤概率按照部件的毁伤准则计算. 计算中考虑破片的入射速度、入射方向、质量等参数，以及致命性部件和非致命性部件之间的遮挡效应. 破片侵彻过程中的速度和质量衰减采用THOR 方程计算，以弹道极限v50作为单条射击线的停机准则.

多枚破片打击下的毁伤概率采用马尔科夫链法[27].马尔科夫链法根据打击的先后次序逐步求出飞机累积毁伤概率. 当余度部件较多时，为避免马尔科夫转换矩阵维数增长造成的组合爆炸现象，采用蒙特卡洛方法，通过随机均匀抽样计算多击毁伤概率. 最终，单个爆炸点的毁伤概率是所有破片对应扫描线的累积毁伤概率.

5 仿真算例与分析

本文选择4 组典型交会条件进行毁伤效果分析，如表1 所示. 弹道1、2 从上方攻击，导弹速度较高，其中弹道1 从预警机的左后方攻击，弹道2 从前方攻击. 弹道3、4 从下方攻击，导弹速度较低，其中弹道3 从右下方攻击，弹道4 从后攻击.

表1 导弹交会参数Tab. 1 Intercept parameters of the missile

在给定的交会弹道条件下，毁伤概率还受到制导误差和瞄准中心位置等因素的影响；若采用预设的固定起爆延迟，还受到预设起爆延迟的影响. 以下对上述因素的影响进行分析. 其余的引信与战斗部参数如表2 所示. 引信探测起爆计算中，径向距离计算步长为0.1 m，计算范围为-20～20 m；扫描线倾角和旋转角的采样间隔分别为7°、30°. 每组交会条件随机生成500 个爆炸点.

表2 引信与战斗部参数Tab. 2 Fuze and warhead parameters

5.1 起爆延迟的影响分析

两条弹道下，CEP 为10 m，瞄准中心为几何中心，分别采用0，5，10，15，20 ms 固定延迟起爆和采用自适应延迟起爆的毁伤概率如图11 所示. 自适应延迟起爆的毁伤概率高于固定延迟起爆，证明了自适应延迟起爆的优越性. 采用固定延迟时，毁伤概率随延迟先增大后减小，存在一个最佳值. 3 个毁伤等级的变化规律相近，整体上C 级高于B 级高于KK 级. 4条弹道的毁伤概率差异较大，弹道2 的最佳延迟在5 ms 左右，其余在10 ms 左右. 采用自适应延迟时，弹道1、2、3 的毁伤概率相近，弹道4 的毁伤概率更高.

图12 是弹道1 采用自适应延迟起爆和5 ms 固定延迟起爆的爆炸点云图对比. 自适应起延迟爆的爆炸点呈漏斗状分布：离瞄准中心远的爆炸点脱靶距离大，起爆延迟小，起爆位置靠后；离瞄准中心近的爆炸点则起爆位置靠前. 由于目标瞄准中心处在破片飞散区中，这些爆炸点都有较高的毁伤概率，大多在80 %以上. 此时，平均毁伤概率主要取决于起爆概率，即成功探测并起爆的样本点比例. 图11 中弹道1 和弹道2 自适应延迟的起爆率分别为82.8 %和83.0 %，较为接近，从而毁伤概率也较为接近，分别为82.1 %和81.6 %. 固定延迟的爆炸点形成了一个围绕目标的包络，探测位置离瞄准中心较远的爆炸点，其命中目标的破片数少，毁伤概率也就较小. 不同交会条件下形成的包络不同，起爆概率不再是决定毁伤概率的唯一因素，因此图11 中两条弹道的毁伤概率曲线也有所差异.

图11 不同起爆延迟的毁伤概率Fig. 11 Kill probabilities for different detonation delays

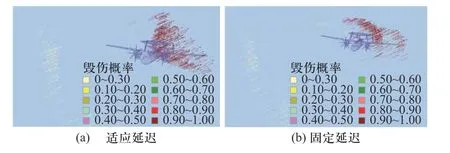
图12 固定延迟与自适应延迟的炸点云图对比Fig. 12 Comparison of detonation point nephogram between fixed delays and self-adaptive delays

5.2 制导误差的影响分析

4 条弹道下，采用5 ms 固定延迟起爆，瞄准中心为几何中心，CEP 分别为5，10，15，20 m 时的毁伤概率Pk如图13 所示. 整体上，毁伤概率随CEP 的升高而降低. 但弹道3、4 在CEP 为5 m 时的毁伤概率反而低于CEP 为10 m 的概率，这是由于其特定的交会方位使得当CEP 增大时，制导误差较大、处于外围爆炸点的破片威力场反而覆盖了更多的致命性部件. 4条弹道的毁伤概率差异较大，且CEP 越小，差异越大.

图13 固定延迟不同制导误差的毁伤概率Fig. 13 Kill probabilities for different CEPs with fixed-delay detonation

4 条弹道下，采用自适应延迟起爆，其余条件同上，毁伤概率Pk和起爆概率Pdet如图14、图15 所示.起爆概率与C 级毁伤概率基本一致，说明引信成功探测和起爆的样本点，其毁伤概率接近1，起爆概率是决定毁伤概率的主要因素. 与固定延迟起爆相比，4 条弹道之间的差异显著缩小；CEP 越小，差异越小.相同CEP 下，各等级、各弹道的毁伤概率也显著高于相应固定延迟起爆的毁伤概率. 与图11 的结果一致，弹道4 的毁伤概率高于其他弹道. 4 条弹道的暴露面积分别为72.68，73.35，69.12，98.05 m2，由此可见暴露面积对起爆和毁伤概率起到了重要影响. 弹道4 的暴露面积更大，从而有更多的样本点可以探测到目标并起爆，毁伤概率也就更大.

图14 自适应延迟不同制导误差的毁伤概率Fig. 14 Kill probabilities for different CEPs with self-adaptively-delayed detonation

图15 自适应延迟不同制导误差的起爆概率Fig. 15 Detonation probabilities for different CEPs with self-adaptivelydelayed detonation

5.3 瞄准中心的影响分析

导弹通常以目标的几何中心或重要部位作为瞄准中心. 对预警机任务级毁伤而言，重要的部位有驾驶舱、设备舱段、任务舱段和雷达天线. 两条弹道下，采用自适应延迟起爆，CEP 为10 m，瞄准中心分别为驾驶舱中心、设备舱段中心、任务舱段中心、雷达罩中心以及飞机几何中心时的毁伤概率如图16 所示.

图16 不同瞄准中心的毁伤概率Fig. 16 Kill probabilities for different CEPs

对于KK 级和B 级，瞄准中心为几何中心中时的毁伤概率均为最高. 对于C 级，4 条弹道毁伤概率最高的瞄准中心分别为任务舱段中心、几何中心、雷达罩中心. 弹道1、2、3 瞄准中心为几何中心时，毁伤概率与最高毁伤概率的差距不超过3%，因此几何中心仍是毁伤概率最高的瞄准中心之一.

对同一条弹道而言，弹道方向上的暴露面积相同，但不同瞄准中心的起爆概率和毁伤概率不同，瞄准中心靠近机头时毁伤概率较低. 这是因为，瞄准中心靠近中部时，脱靶距离较大的样本点仍有可能探测到目标；而靠近头部时，脱靶距离较大的样本点会掠过目标，无法起爆. 以弹道2 为例，图17 是OXrYr平面的二维示意图，当瞄准中心在几何中心时，以脱靶距离ρ0限定的阴影区域内的样本点均能探测到目标. 当瞄准中心在驾驶舱中心时，绿色阴影内的样本点无法探测到目标，从而起爆概率较低，毁伤概率也较低. 因此，起爆概率不仅取决于暴露面积，还受到瞄准中心的影响.

图17 瞄准中心对起爆概率的影响Fig. 17 Effects of aiming centers on detonation probability

6 结 论

本文研究了近炸引信和破片式战斗部导弹对典型预警机的毁伤效果及其影响因素. 建立了预警机的KK、B 和C 级易损性模型以及引信探测和自适应延迟起爆模型，以此计算单个爆炸点的毁伤概率，并采用蒙特卡洛方法计算给定交会条件和制导精度下的平均毁伤概率. 通过仿真分析了交会条件、起爆延迟、制导误差和瞄准中心等因素对毁伤概率的影响.得到的主要结论如下.

① 除运输机典型的致命性部件外，预警机任务级致命性部件还包括雷达、敌我识别、电子侦察、通信、导航、指挥控制等任务系统的天线、信息处理设备和任务人员. 致命性部件在中、前机身较为集中.

② 自适应延迟起爆的毁伤概率高于固定延迟起爆，且减小了交会条件对毁伤概率的影响.

③ 采用自适应延迟起爆时：毁伤概率主要取决于起爆概率，起爆概率主要受暴露面积和瞄准中心的影响；制导精度的提高可以减小交会条件的影响；以几何中心为瞄准中心的毁伤概率较高.

本文主要研究了破片对系统部件的毁伤，并在引信探测模型中假设面元能够完整反射信号. 今后研究需要进一步分析冲击波毁伤，以及战斗部对气动外形和结构传力的破坏造成的毁伤，并在引信探测模型中进一步考虑面元的散射效应，从而更准确地评估战斗部对预警机的毁伤效果.