复杂结构飞行器的飞行载荷建模方法研究
2022-04-24陈致名唐宁范华飞
陈致名,唐宁,范华飞
(中国飞行试验研究院飞机所,西安710089)
0 引言
根据国军标及相关适航条例要求,飞行载荷测量试验是验证飞机结构设计、完成新机定型必须完成的试验项目。飞行载荷的测量方法有两种:应变法和压力测量法,应变法用于测量结构载荷,压力测量法用于测量气动载荷,由于压力测量法对环境要求较高,因此飞行载荷测量常选用应变法。应变法利用在蒙皮、梁腹板及上下缘条等结构改装的应变片,通过地面载荷校准试验建立结构载荷与应变之间的关系,在飞行数据处理过程中,结合应变数据及相关飞行参数,可以计算飞机各剖面结构载荷,并估算出气动载荷。
基于应变法载荷测量的传统建模方法分为穷举法和遗传算法。T.H.Skopinski 等采用穷举法建立了简单双梁结构机翼的载荷模型;赵燕等在遗传算法的基础上结合飞行载荷建模原理提出了改进遗传算法,并利用其建立载荷模型,得到了较好的结果;唐宁等考虑了概差对载荷模型的影响,同时通过支持向量机方法给出了基于飞行参数的飞行载荷模型建立方法,该方法将传统建模方法所得数据与飞行参数相关联,充分利用了飞行数据,在采用传统方法建立载荷模型后,可用于飞行载荷测量架机同型号其余架机的载荷监控;金鑫等通过深度学习方法基于有限元计算结果给出了通过少量应变采样点反演全局载荷分布的方法。由于目前技术条件限制,国内外鲜见测量翼面全局结构载荷分布的方法,因此尚无实测数据与该方法基于有限元结果计算所得数据相验证,且由于应变实测坐标与对应节点坐标存在偏差,同时实际测得应变并非节点绝对应变,该方法用于飞行载荷实测尚需其余技术支持。
随着作战需求日益提高,为了满足刚度与强度的要求,大量战斗机的机翼、尾翼采用多梁多墙等复杂结构,全机载荷的传力路径极为复杂,无法通过相关理论准确分析各结构受载情况。为了避免遗漏载荷的主传力路径,会在多梁多墙结构飞行器的所有可能受载部位(梁与墙的交点处)布置应变计,导致载荷模型可选的电桥数量大幅度提升。穷举法由于对电桥筛选能力较差,所得载荷模型误差变大;遗传算法在其产生种群过程中为保证精度产生大量个体,计算个体拟合度时耗时较长,效率降低。
基于此,本文通过改进飞行载荷建模过程中载荷模型的迭代方法,提出一种适用于复杂结构飞行器的飞行载荷改进建模方法,将改进方法与传统方法所得载荷模型的误差进行对比,并基于试飞数据对改进方法所得载荷模型进行验证。
1 飞行载荷建模原理
建立载荷模型的基础是地面载荷校准试验,通过寻找结构载荷与应变之间的关系,进而建立载荷模型。通常外载荷与应变计输出信号之间的关系可以认为是线性的,但是加载时结构会受到拉压力、剪力、弯矩和扭矩的综合影响,不同的外载荷可能会使某个电桥产生同样的信号输出,可以通过不同应变计电桥的惠斯通电桥形式及载荷校准试验所建立的载荷方程将载荷进行解耦。
由于复杂结构中结构载荷的传力路径难以准确分析,需要将剖面上不同位置的电桥所感受到的力特性综合分析,计算剖面的结构受载情况。载荷方程的广义形式如下:
=++…+kμ+…+kμ(1)
式中:为结构载荷;k为载荷方程中电桥对应的拟合系数;μ为电桥的输出。
理想的载荷方程应符合以下关系:
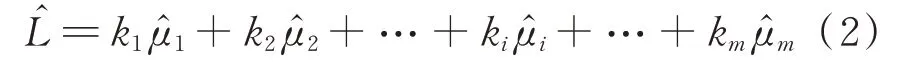
式中:̂为飞机在飞行中实际受到的外载荷;̂为电桥的输出。
2 飞行载荷建模方法
2.1 传统方法
穷举法的建模原理是在利用所有电桥获得载荷方程后,通过逐轮淘汰电桥的方式给出载荷方程集。筛选过程中由算法分析淘汰电桥,利用剩余电桥重新建立载荷方程,重复进行电桥筛选与模型建立,直到剩下两个电桥时停止筛选,形成电桥数量由多到少的载荷方程集。总电桥数为时,穷举法计算过程中所形成的方程集数量如式(3)所示。

遗传算法的建模原理是将单个电桥进行组合,定义指标判断电桥组合后载荷方程的优劣,实行优胜劣汰制逐步添加新的电桥,形成电桥数量由少到多的载荷方程集。总电桥数为、遗传比例为时,遗传算法计算过程中所形成的种群数量如式(4)所示。

穷举法和遗传算法在方程迭代的过程中分别考虑了电桥及载荷方程的优劣。但是对于复杂结构,由式(3)~式(4)可知,电桥数量的增加使遗传算法中种群数量急速增加,后续拟合度计算尤为复杂,相比于穷举法计算耗费时间较长,在处理大量数据时效率较低;穷举法的计算效率虽然可以满足要求,但是随着电桥数量的增加,电桥间的差异性降低,通过筛选淘汰单个电桥易积累误差,在淘汰多个电桥后使最后的载荷方程误差大于最优载荷方程误差。
2.2 改进方法
2.2.1 建模
以穷举法为基础,改进方法的流程框图如图1所示。

图1 改进方法流程框图Fig.1 Improved method flow diagram
相比于穷举法,改进方法在方程迭代的过程中给出了将某电桥淘汰后新方程的筛选指标,将其定义为方程筛选指标。令方程筛选指标与电桥筛选指标融合为新的综合指标,利用该指标筛选电桥,生成新方程。
电桥筛选指标的定义为

式中:k为电桥响应系数;λ为电桥响应与校准载荷之间的相关系数;β为载荷模型中电桥的拟合系数;γ为电桥复相关系数;τ为电桥的冗余度。
方程筛选指标的定义为
=S+V++(6)
式中:S为方程的建模误差;V为方程的检验误差;为方程的不相关性;为方程的冗余度。
由于改进方法以穷举法为基础,增加的方程筛选指标在电桥较少时对各个电桥影响较小,因此对于简单结构飞行器,结果与穷举法相似。通常情况下改进方法同样适用于简单结构飞行器的飞行载荷测量。
2.2.2 无量纲处理
在融合电桥筛选指标和方程筛选指标之前,需要将两者进行无量纲处理。

在式(7)~式(8)中,假设当前载荷方程由一组电桥构成,则min与min为这组电桥中最小的电桥筛选指标与方程筛选指标,max与max为这组电桥中最大的电桥筛选指标与方程筛选指标。
这种处理方法使电桥筛选指标与方程筛选指标都在[0,1]之间。
3 飞行载荷模型对比
对某型机的机翼开展载荷校准试验,由于该型机机翼为多梁多墙结构,因此布置较多的剪力、弯矩及扭矩电桥,由于机翼载荷主要为弯矩及剪力,且受目前技术限制,应变法测量扭矩载荷误差较大,因此本文主要比较穷举法和改进方法计算弯矩及剪力的结果。
利用机翼上、、剖面的试验数据,从剖面上所有电桥都用于建立载荷方程开始,分别使用两种方法循环筛选电桥,并利用检验工况计算误差,误差计算方法为


目前测量多梁多墙结构飞行器飞行载荷时,弯矩测量结果较为理想,而剪力测量结果较差,不同方法测量结果区别较大,因此本文主要关注两种方法对剪力方程产生的影响。剖面的弯矩测量结果误差对比如图2 所示,方程1 为选用所有可选电桥的初始载荷方程。

图2 两种方法所得c剖面弯矩方程误差对比Fig.2 Error comparison ofc-section moment equation obtained by two methods
在、、剖面上,两种方法所得剪力测量结果误差对比如图3 所示(图中误差已做取整处理)。
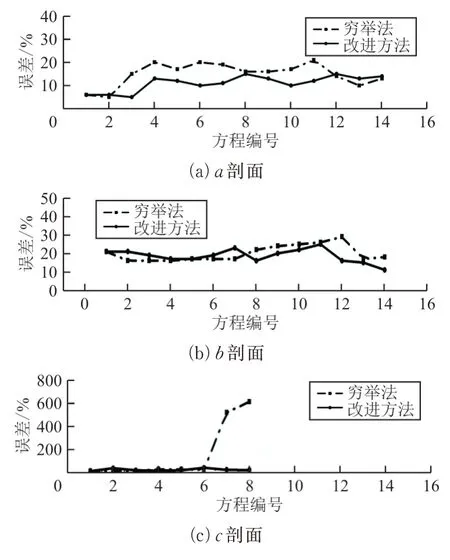
图3 两种方法所得a、b、c剖面剪力方程误差对比Fig.3 Error comparisons in the shear equations of profilesa,bandcobtained by two methods
图2~图3 中的误差值如表1 所示(由于剖面电桥较少,因此迭代产生的方程也较少)。

表1 各剖面方程检验误差Table 1 error of each profile equation单位:%
从表1 可以看出:在方程迭代过程初期,各剖面改进方法算得的结果误差较大,随着循环次数增加,改进方法算得的结果误差均小于穷举法或与其接近。其原因为受改装工艺限制,当电桥数量较多时会产生个别电桥特性较差的问题,由于穷举法的筛选依据只有电桥特性,因此可在首轮筛选过程中将特性较差的电桥剔除掉,而改进方法的筛选依据考虑了方程误差、方程特性等因素,电桥可能会在随后几轮筛选过程中被剔除掉。由于飞行载荷实测时,某些应变计会受各种因素影响发生零漂或温漂等现象,影响数据精度,因此通常情况下为了保证载荷模型稳定度,电桥数量需确保在6 个以内,即表1 内各剖面倒数3 个方程为可用方程,其余方程不能应用于飞行载荷监测,因此对于复杂结构飞行器,改进方法所得载荷模型可以减小个别特性较差电桥引起的影响。
从表1 也可以看出:随着电桥的筛选,剖面穷举法算得剪力方程结果误差急剧增加。其原因为穷举法算得方程7 由3 个弯矩电桥构成,改进方法算得方程7 由2 个剪力电桥1 个弯矩电桥构成,由于弯矩电桥对剪力敏感度低,因此全选用弯矩电桥建立的载荷方程误差较大。但是为了将剪力与弯矩对载荷方程的影响进行解耦,建立剪力方程时两种电桥均需考虑。电桥筛选指标中考虑了电桥对载荷的相应系数及电桥特性,其权重接近,而改进方法中加入了方程筛选指标,使方程误差对电桥筛选逻辑产生影响,所得载荷方程精度与可信度更高。
4 飞行载荷实测与分析
将该型机飞行中得到的实测应变数据代入改进方法所得的载荷模型,即可对改进方法所得模型进行验证。以剖面为例,采用改进方法所得剪力模型的方程5 以及弯矩模型的方程5 计算实测载荷,将其与真实飞行参数进行对比。在俯仰机动下,剖面弯矩、剪力、法向过载、迎角及纵向杆位移的时间历程如图4 所示。
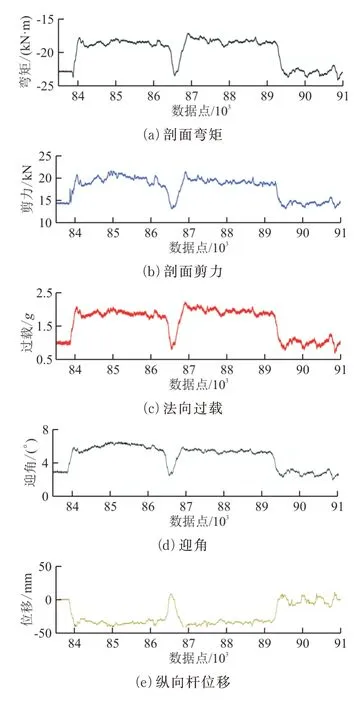
图4 某型机俯仰机动的剖面载荷与飞行参数的时间历程Fig.4 Time history of profile loads and flight parameters of a certain aircraft in pitch maneuver
从图4 可以看出:飞行员配平飞机后急剧拉杆并进行了一次回弹,使飞机达到目标过载,完成俯仰机动。
在滚转机动下,剖面弯矩、剪力、法向过载、滚转角及横向杆位移的时间历程如图5 所示。

图5 某型机滚转机动的剖面载荷与飞行参数的时间历程Fig.5 Time history of profile loads and flight parameters of a certain aircraft in roll maneuver
从图5 可以看出:飞行员配平飞机后先后向两个方向倾斜操纵杆,使飞机达到目标滚转角,完成滚转机动;飞行器在俯仰、滚转机动飞行时,剖面弯矩减小,俯仰机动过载提升时,剖面剪力显著增加,机动中改进方法算得的载荷结果变化趋势符合预期。
基于飞行参数分析载荷方程的适用性,在图4~图5 中,两机动中1过载平飞状态下,剖面外侧剪力接近,将对应状态下飞机设计数据中剖面外侧气动载荷换算为结构载荷,并与两机动中1过载平飞时剖面外侧载荷进行对比,改进方法算得的误差为16%,低于20%的剪力误差要求,穷举法所得剪力方程7 算得的误差为24%,因此对于剖面来说,改进方法算得的载荷方程更适于监控飞行载荷。
5 结论
(1)本文提出的飞行载荷改进建模方法适用于复杂结构飞行器的飞行载荷建模,模型精度及迭代稳定性较好。
(2)改进方法迭代生成的剪力方程误差较小,对于弯矩方程来说,两种方法误差相近,都可以满足要求。
(3)飞行实测中,改进方法所得载荷模型的精度有一定的提升,改进方法对该型机后续飞行载荷测量有一定的借鉴意义。
