新型双纤芯大模场光纤传感特性研究

张 辉,周仁龙,杨 飒,李 勇

(广东第二师范学院物理与信息工程学院，广东 广州 513030)

1 引 言

随着纳米技术的发展,表面等离子体(Surface Plasmon Polaritons,SPPs)越来越引起纳米光子学的兴趣[1]。由于粒子的可操纵性[2],自成像[3],学术界已经提出了各种非衍射表面等离子体束,例如艾里光束[4-5],贝塞尔光束[6]和余弦高斯光束[7]。石墨烯作为新型的二维(2D)材料,在太赫兹和远红外频率中其表面电导率几乎是纯虚数,其化学势可通过化学掺杂或控制栅极电压来动态调节[8-9]。石墨烯的单一碳原子层能通过外部施加的电压来吸引其独特的光电性能,具有极宽的波长范围。这些优异性能显示石墨烯是实现包括光电探测器[10],宽带宽的光学偏振器[11],高速光调制器[12-13]等光子和光电器件的良好材料。此外,石墨烯还是用作等离子体应用的材料。混合涂覆的等离子体微腔和石墨烯在实现可调光调制上有着非常好的前景。表面等离子体共振(Surface Plasmon Resonance,SPR)是电磁波在金属界面出现全反射时激发的自由电子密度振荡[14-16],因其检测周围介质的折射率(Refractive Index,RI)变化的高灵敏度而备受关注。这些属性提供了动态操控基于石墨烯平台中光纤表面等离子体共振传感器的可能性。因此,将石墨烯材料集成到传统的光学等离子体波导传感器中[17-18],形成的光纤表面等离子体共振传感器不仅体积小,能耗低,检测速度快,抗电磁干扰强,支持实时在线检测,还具备SPR检测技术的高效灵敏[19],检测时无需标记即可进行实时动态检测的优点,日益成为生化检测传感领域的研究热点。

作为典型应用之一的光纤激光器,其光束质量高,亮度高、阈值低,在医疗设备、激光武器、遥感测控、光纤通信等重要领域都有广泛的应用。2006年,John M.Fini报道说,抛物面型纤维具有天然弯曲的电阻特性,在弯曲下具有大模场面积和良好的抑制高阶模特性[20]。然而传统的制造技术难以制造很大面积的纤芯。2013年,Deepak Jain等报道称,多沟道光纤可以实现超大模场面积和良好的高阶模抑制[21]。然而,在弯曲的情况下,多沟道光纤的性能变差。随着激光器功率的提升,非线性效应和模式不稳定的缺点成为进一步提升光纤输出光功率的最大障碍。由于非线性效应产生的阈值功率与光纤的有效模场面积成正比,所以提高有效模场面积能降低光纤中光功率密度,从而减小非线性效应。保持激光器的单模运行,可以提高激光器输出光束的质量。

在这项工作中,研究了二维材料对杂化等离子体光子结构的表面等离子体极化激发的影响,以及该杂化等离子体传感器的传感性能。具体地,提出了一种由双纤芯的组成的等离子光纤模型,应用有限元分析方法进行特征模型分析[22],研究石墨烯层附加在金属膜上引起的谐振耦合。探究了石墨烯-金属传感膜辅助光纤结构的详细特性,并计算了模型的有效模场指数和有效模场面积。因光纤的性能特征在于其泄漏损失,因此研究了泄漏损耗如何取决于光纤的物理参数。结果揭示了石墨烯层强化了表面等离子体极化(SPP)的电场。高阶的入射光波模式会为传感器带来高的灵敏度,但同时也带来了低的品质因子;在传感层厚度分布不均匀的情况下,传感区长度对传感器性能的影响较为明显。

2 设备结构与理论分析

图1 石墨烯-金属双纤芯结构的示意性结构图

石墨烯-金属感测膜辅助纤芯结构的折射率分布是通过径向有效折射率法(Radial Effective refractive Index Method,REIM)获得的。由于折射率差Δn≪1,因此电场的横向分量满足标量波。用有限元方法(Finite Element Method,FEM)讨论光纤性能。有限元是最广泛应用于建模复杂的、高精度的光纤结构,因此,我们结合使用完整的矢量有限元方法与完美匹配层(Perfect Matching Layer,PML)的边界条件,将20 μm厚的圆形PML设置在包层外侧。方程在圆柱坐标系中表示为[18-19]:

(1)

其中,φ是相关的电场或磁场;k0=2π/λ表示自由空间波数;n(r,θ)是折射率分布;r表示径向坐标。模场分布可以用以下表达式表示:

φ(r,θ)=R(r)Θ(r,θ)

(2)

结合方程(2),方程(1)可以进一步简化为:

(3)

光纤的两个主要性能分别是模场面积和模式损耗,主要指的是基模的模场面积,在入射功率恒定的前提下,可以反应光纤的功率密度值。大模场面积可以有效地减小受激拉曼散射之类的非线性效应。有效模场面积Aeff是用于描述的光纤激光器的功率密度的重要参数。它可以通过公式(4)计算:

(4)

其中,E是横向电场的Ex分量的大小。

光纤中各模式的泄漏损耗可以由传输常数的虚部求解而得,公式由(5)给出:

(5)

其中,neff是各模式的有效折射率;λ是入射波长,用高阶模损耗与基模损耗的比值来判断光纤是否实现了单模运转,其公式定义为(6)所示:

(6)

其中,分子Loss(lowest-HOMs)指的是最小高阶模损耗;分母Loss(FM)指的是基模损耗,当两者的比值达到某一个参考值时,可以认为光纤中的高阶模全部泄漏只剩下了单模传输。

根据所采用的介质结构层参数:纤芯的折射率n_core=1.4460,包层的折射率n_cladding=1.4453,石墨烯上部覆盖物样品的折射率n_sample=1.333,单层石墨烯的厚度t_G=N×0.34 nm,石墨烯的层数N=1,纤芯的半径r_core=8 μm,包层的边长r_cladding=15 μm,金属层的厚度t_metal=30 nm,光纤中的传播波长λ=600 nm,通过数值计算得到光纤基模的模场特性,其模式分布如图2所示,下角标a和b分别表示双纤芯结构中的两个纤芯。从能量流密度可以看出,该模式在纤芯与石墨烯和金属之间具有着强耦合,电场呈现典型的高斯分布,SPP的电场在金属薄膜表面最强,然后以指数规律衰减。图中的黑色箭头表示归一化的金薄膜激发的SPP的电场分布。零位置是金属膜和侧面抛光小平面之间的边界。

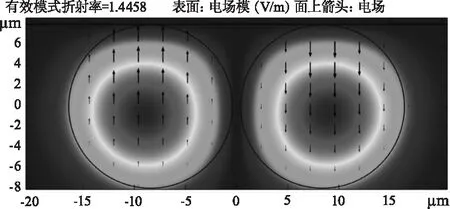
(a)LP01a模模场分布

3 数值模拟与结果分析

3.1 不同石墨烯层数激发的归一化电场强度

考虑石墨烯厚度不同,对电磁波的吸收能力也相应不同,研究石墨烯层数的改变对归一化电场强度的影响。根据所采用的介质结构层参数:纤芯的折射率n_core=1.4478,包层的折射率n_cladding=1.4453,石墨烯上部覆盖物样品的折射率n_sample=1.333,单层石墨烯的厚度t_G=N×0.34 nm,纤芯的半径r_core=8 μm,包层的边长r_cladding=15 μm,金属层的厚度t_metal=30 nm,光纤中的传播波长λ=600 nm,通过数值计算在图3(a)中绘制了包括电介质、金属膜、纤芯、光纤包层的模型的电场分布,显示了涂覆在30 nm金属层上的单层石墨烯、五层石墨烯和十层石墨烯的LP01模式的归一化电场强度,由图3(a)可见,在0～0.04 μm的位置,SPP的归一化电场强度有所增强,说明涂覆了石墨烯层之后,增强且激发了SPP,研究显示,在金属层上增加单层石墨烯,SPP的强度大约能提高30.2 %。继续增加石墨烯的层数,反而会降低SPP的强度,而不是进一步提高。这是因为额外的石墨烯层会引起较大的电子能量损失,从而导致SPP的逐渐降低。由此可见,单层石墨烯对电介质的变化提供了最佳的灵敏度。图(b)是LP01模式在整个模拟几何图形上沿着y方向的归一化电场强度的分布图。

(a)

3.2 涂覆石墨烯-金属的双纤芯结构参数与波长的关系

介质结构层参数设定为:纤芯的折射率n_core=1.4478,包层的折射率n_cladding=1.4453,石墨烯上部覆盖物样品的折射率n_sample=1.333,单层石墨烯的厚度t_G=N×0.34 nm,纤芯的半径r_core=8 μm,包层的边长r_cladding=15 μm,石墨烯的层数N=1,金属层的厚度t_metal=30 nm,光纤中的传播波长λ=600 nm,对于涂覆石墨烯-金属的双纤芯结构,其基本纤芯模式LP01a模和LP01b模与高阶纤芯模式LP11模的有效模指数neff随波长变化的关系如图4(a)所示。由于双纤芯结构的对称性,LP01a模和LP01b模的线型有相似性。有效模指数随着波长的增加而减小。图4(b)显示了不同波长下,基本纤芯模式和高阶纤芯模式的衰减率dB(rad/m)变化情况。由于纤芯和石墨烯-金属之间有很强的耦合,衰减常数在波长为630～660 nm之间的范围有很大的波动,基本纤芯模式LP01模达到了350 dB的衰减率,高阶纤芯模式LP11模则达到了160 dB的衰减率。

(a)有效模指数与波长关系

图4(c)进一步显示了基本纤芯模式LP01模和高阶纤芯模式LP11模的有效模场面积特性。对应于不同波长的石墨烯区域的有效模场面积,以波长630 nm为界,小于630 nm时,有效模场面积急速随着波长的增大而增大；大于630 nm时,有效模场面积只缓慢随波长的增大而增大。在图4(d)中,还用不同的波长绘制了光纤区域的两种模式的有效模场面积,两种模式的面积均随着波长的增加而增加,但是基本纤芯模式LP01模的有效模场面积增加速率明显比高阶纤芯模式LP11模的有效模场面积增加速率要快很多。由于非线性效应和模式不稳定这两个因素限制了激光器功率的提升以及激光器输出的光束质量,故提高光纤区域的摸场面积能降低光纤中光功率的密度,进一步能减少非线性带来的不利影响,同时可以避免功率密度过大造成的物理影响。另外,保持激光器的单模运行能提高激光器的稳定性,保证高质量的输出光束。图4(d)中显示了基本纤芯模式LP01模的有效模场面积增长速率比高阶纤芯模式LP11模的增长速率要快,表明在满足单模运行的前提下,获得了大模场面积,这对激光器功率的提升大有益处。

3.3 不含金属层的石墨烯双纤芯结构参数与波长的关系

考虑不含金属层的石墨烯双纤芯结构的性能,研究其结构参数和波长的关系。介质结构层参数设定为:纤芯折射率n_core=1.4478,包层折射率n_cladding=1.4453,石墨烯上部覆盖物样品的折射率n_sample=1.333,单层石墨烯厚度t_G=N×0.34 nm,纤芯半径r_core=8 μm,包层边长r_cladding=15 μm,石墨烯层数N=1,金属层厚度t_metal=0 nm,光纤中的传播波长λ=600 nm,由图5(a)可知,同样是在波长600～1000 nm区间,不含金属层的有效模指数与含有金属层的有效模指数变化不大,而衰减率的变化就相当的大,如图5(b)所示,这是由于不含金属层时,石墨烯与光纤之间的耦合较弱,导致与金属-石墨烯的双纤芯结构相比,衰减率dB降低。

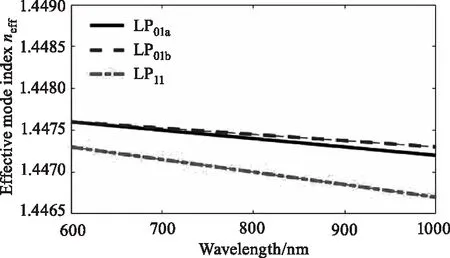
(a)有效模指数与波长关系

图5(c)中显示的是两种模式下的石墨烯区的有效模面积与波长的关系。与石墨烯-金属双纤芯结构的石墨烯区的有效模面积明显不同的是,两种模式的有效模面积在波长600～1000 nm区间的增长速率保持一致,没有发生增长速率的突变。图5(d)纤芯区有效模面积曲线与石墨烯-金属双纤芯结构的纤芯区有效模面积曲线基本一致,变化不大。

3.4 纤芯折射率对光纤性能的影响

为了抑制高阶模,保证基模传输,通过改变纤芯的折射率分布是光纤结构设计的方法之一。为此,我们对纤芯折射率从1.4460到1.4496区间的有效模指数、衰减率、石墨烯的有效模场面积和纤芯区的有效模场面积做了分析。不同纤芯折射率对光纤性能的影响如图6所示,其中,光纤参数设定为包层折射率n_cladding=1.4453,纤芯半径r_core=8 μm,包层边长r_cladding=15 μm,金属层厚度t_metal=30 nm,光纤中的传播波长λ=600 nm。通过数值计算结果表明:纤芯折射率的改变对基模衰减率的影响很小,由图6(b)可见,衰减率基本保持不变。而从图6(d)可见,当纤芯折射率是1.4460时,基模的有效模场面积为275 μm2,此面积大于之前不含金属层的波长为600 nm时基模的有效模场面积250 μm2,也大于含有金属层的波长为600 nm的基模有效模场面积249 μm2,说明选择恰当的纤芯折射率,能有效提高模场面积,减小光纤的非线性效应。在实际使用中,应根据实际情况进行纤芯折射率的选择。

(a)有效模指数与纤芯折射率的关系

3.5 金属层厚度、石墨烯层数和纤芯折射率对品质因子的影响

品质因子Q是研究传感性能的一项重要指标参量,光学微腔由于其高品质因子特性具有广泛的应用前景。考虑影响品质因子Q的几种因素,包括金属层厚度、石墨烯层数和纤芯的折射率,介质结构层参数设定为:纤芯折射率n_core=1.4478,包层折射率n_cladding=1.4453,石墨烯上部覆盖物样品的折射率n_sample=1.333,单层石墨烯厚度t_G=N×0.34 nm,纤芯半径r_core=8 μm,包层边长r_cladding=15 μm,石墨烯层数N=1,金属层厚度t_metal=30 nm,光纤中的传播波长λ=600 nm,经数值模拟计算可知在23层石墨烯时品质因子能达到1.99×108,金属层厚度在90层时,品质因子大约是2.03×108,而纤芯的折射率与品质因子呈单调上升的关系,如图7所示。

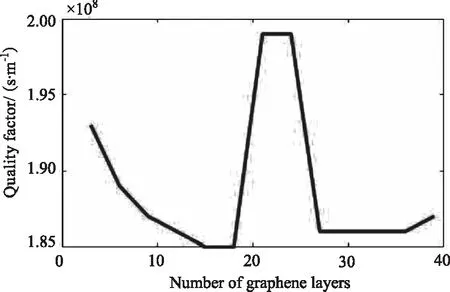
(a)石墨烯层数与品质因子的关系

4 结 论

针对金属-石墨烯结构的双纤芯结构,通过数值模拟研究了等离子体光子结构的变化对表面激励(SPP)的影响以及该等离子体传感器的感测性能。并且对涂覆金属层和不涂覆金属层两种情况下,不同波长范围内的纤芯区的有效模指数、衰减常数、石墨烯的有效模面积和纤芯区的有效模面积进行了分析。数据表明选择合适的纤芯折射率,能在600 nm波长段提高基模的有效模场面积到275 μm2,高于同等600 nm波长情况下其他纤芯折射率数值的有效模场面积,达到了减小光纤非线性效应的效果。文中提出的双纤芯结构的传感器具有独特的传感性能,具备实现感测应用中的高度敏感,高度集成,灵活和小型化的前景。