基于直观想象的“全等三角形的复习课”教学思考
2022-04-23陈黎雨
陈黎雨

关键词:直观想象;对称性;全等三角形
一、培养直观想象能力的重要性
培养学生的直观想象能力,是数学学科核心素养落地的重要标志之一。直观想象是发现和提出问题、分析和解决问题的重要手段,是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础。
直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素養。主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路。[1]
只有学生具有了良好的直观想象能力,并且将这种能力迁移到所有领域的问题解决过程中,其他五个核心素养的落地才更具有可行性。[2]
二、培养直观想象能力的方法
直观想象能力的培养离不开训练学生识图构图的思维方式,看问题的角度决定了学生是否能够发现和提出问题。在新课程标准中,“图形与几何”的设置包含了三个专题:“图形的性质”、“图形的变化”、“图形与坐标”,平时教学中,学生对于基本图形性质中的“元素之间的关系”与“对称性”的学习较为割裂,学生在复杂的图形中难以区分基本图形,根据图形的变化想象构造图形并探索解决问题的方向,因此教师应在日常教学中从“图形的变化”的角度引导学生观察基本图形,进一步理解“图形的性质”,再从“图形的性质”解释“图形的变化”,相互融合,最后总结模型,从而促进学生能够主动运用基本图形的对称性分析问题,能通过直观想象猜想、构造图形并探索解决问题的方向.
在组织具体教学的过程中,可以选择“全等三角形的复习课”等课程,以“角”是一个轴对称图形为切入点,将“图形的变化”和“图形的性质”融合在教学过程始终。
(一)从“图形的变化”的角度想象基本图形
学生的直观想象能力的提升并不是一蹴而就的,需要在几何学的课程上培养数学思维方式,识图的方向是很重要的一步,要做到有向有序地识图、分析图,这与教师的在最开始的几何学看图的思维方式有很重要地关联,主要是从“图形的对称性”的角度识图,观察图形与图形之间的位置关系、大小关系,然后再观察元素与元素之间的位置关系、大小关系。
“几何作图”是一个好的载体,作图过程中能分析“图形元素之间的关系”,对培养直观想象能力中的识图构图起着重要的作用。
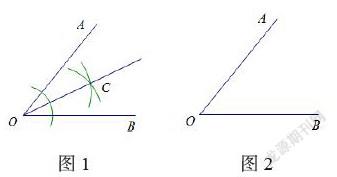
例如:全等三角形的复习课中,如图1,若点C是锐角∠AOB内一点,分别在射线OA和射线OB上确定点E,F,使得△OCE≌△OCF,用尺规确定点C,E,F的位置并说明理由。
直观想象能力首先是对图形有直观的感受,通过画示意图先引导学生观察图形,借助位置关系、大小关系看图形的变化,然后再合理想象图形。画完示意图后引导学生观察这两个三角形△OCE和△OCF的位置关系,观察出共边的全等三角形可以折叠得到,再结合“角是轴对称图形”想象点C的位置,并不是一个固定的点,而是点的集合,在∠AOB的平分线上,如图2。
2.基本“图形的变化”对三角形进行分类讨论
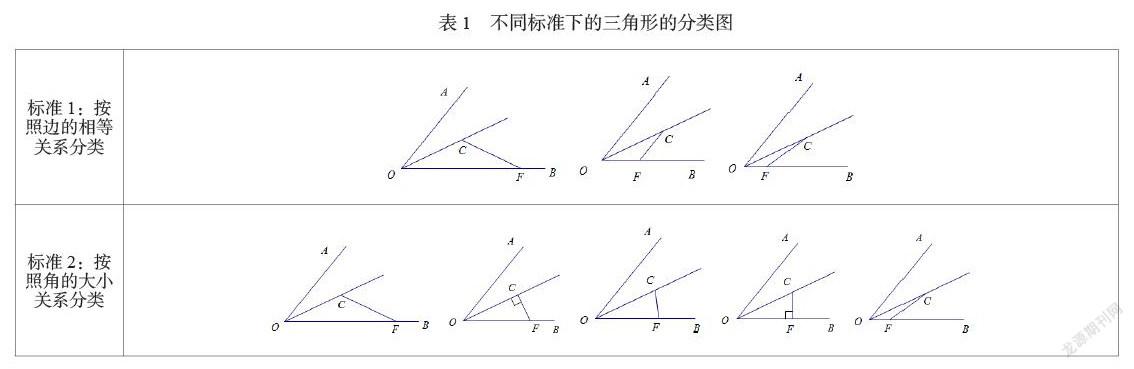
引导学生想象折叠前后的两个三角形会构成什么图形,也就是△OCF沿OC折叠后的△OCE与△OCF会构成什么图形,而这与△OCF的大小和形状有关。由于点F是在射线OB上的动点,△OCF的大小和形状也是不确定的,因此需要进行分类讨论,引导学生根据不同的标准进行讨论,并画出相应的图形。
标准1:按照边的相等关系分类,结合图形可以得到三边都不相等的三角形、等腰三角形;
标准2:按照角的大小关系分类,结合图形可以得到钝角三角形、直角三角形、锐角三角形如下表1.
引导学生根据条件△OCE≌△OCF思考这两个三角形的元素关系,不难看出点E和F是一对对应点,通过追问学生如何在图形上体现对应点引导他们将对应点转化为对应线段或者对应角思考,这样学生的思维也就发散开了。
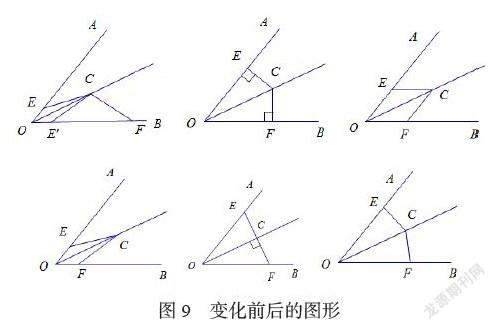
从对应线段来看,可以通过思考OE和OF的关系,不难想到利用圆规分别在OA和OB上截取两条相等的线段就可以确定点E和F的位置,如图3, 再追问学生这样画法下的两个三角形全等的依据,这样也就复习了全等三角形的其中一种判定方法SAS. 还可以通过思考CE和CF的关系,学生会想到以及类比截取OA=OB的方法,以点C为圆心,适当的半径画弧,分别交OA,OB于点E,F,如图4. 再引导观察图形,判断这种画法中点E的位置是否是唯一确定的,如果是,说明判定方法,如果不是,则说明点E的位置还可以在哪里,画出图形如图5. 说明此种画法中线段CE和CF的位置关系并不是对应的,也可以说明SSA不能证明两个三角形全等。
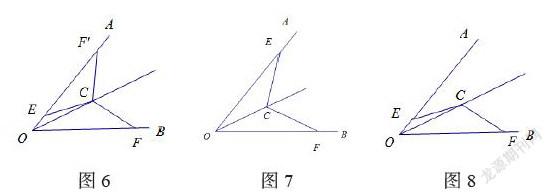
复习了全等三角形的判定后,可利用“角具有对称性”,可用变式题目引导学生从图形变化的角度来构图,例如:如图6,已知OC是∠AOB的平分线,,与之间有怎样的数量关系?引导学生将△OCE沿OC翻折得到如图7,或者将△OCF沿OC翻折得到如图8,探究解题方向后从而有向有序地解决问题。
(三)从“图形的变化”的角度总结模型
具有特殊位置关系的两个全等三角形需要引导学生从图形的变化的角度来识图构图,更重要的是需要进行总结,逐步构建基本图形群以加深学生对基本图形的理解,从而促进学生能够主动运用基本图形分析问题,探求解决问题的方向,最终提升学生的直观想象能力。
综上所述,学生直观想象能力的培养与学生的全面发展有着密不可分的关系。在倡导核素理念下,让学生有向有序地分析几何图形需做到引导学生根据“图形的变化”理解“图形的性质”,根据“图形的性质”解释“图形的变化”,将几何学的三个专题互相融合,最后总结几何模型,因为在几何教学中,如果能经常借助特殊模型,让学生直观感知特殊模型中点、线、面的位置关系,积累图形的表象,增强直观感,养成由直观到想象的思维习惯,则对培养学生的直观想象能力有明显的促进作用[]。
參考文献:
[1] 中华人民共和国教育部制定.普通高中数学课程标准(2017年版). 北京:人民教育出版社, 2018
[2] 许彬城. 基于直观想象素养培养管窥核心素养培育[J]. 数学教学通讯, 2020, 02: 32-33
[3] 徐德同,樊向阳. 例谈初中生直观想象能力的培养[J]. 教育研究与评论(中学教育教学), 2019, 08: 10-13
