破解立体几何动态问题的策略

刘大伟 李勇霞

(重庆市江津中学校)

2021年新高考试题注重对高中数学基础知识、基本技能、基本方法及基本数学思想的考查,具备起点低、跨度大、层次多、角度广的特点,具有学科特点的基础性、综合性、应用性、创新性的考查要求.作为必考知识点的立体几何板块,对点、线、面动态问题的考查力度有增加的趋势,而且该类型试题题型多变、综合性较强、涉及知识面较广、难度相对较大.本文对立体几何中的动态问题进行了梳理归纳,并总结了不同类型试题的解题策略,希望对广大读者有所帮助.

1 借助补形法解决动态问题

利用补形法解决立体几何问题,要围绕已知条件来进行,往往会涉及将棱锥补成棱柱、将台体补成锥体等,即将不规则几何体补成规则几何体进行求解.利用补形法往往起到化繁为简、化难为易的作用.

例1已知三棱锥P-ABC三条侧棱PA,PB,PC两两互相垂直,且PA＝PB＝PC＝2,M,N分别为该三棱锥的内切球和外接球上的动点,则M,N两点间距离的最小值为( ).

由已知可将该三棱锥补成正方体,如图1所示.设三棱锥内切球球心为O1,外接球球心为O2,内切球与平面ABC的切点为G,易知O1,O2,G三点均在PD1上,且PD1⊥平面ABC.设内切球的半径为r,由等体积法可得

图1

本题的求解采用了补形法,通过作出图形,找出内切球,外接球球心,由几何关系知,M,N两点间距离的最小值为PG-2r,结合等体积法可求出内切圆半径r和PG,最终求得结果.

2 借助轨迹方程解决动态问题

对于立体几何中的轨迹问题有两种常见处理方法:1)借助曲线的定义或几何图像的特征识别轨迹类型,如圆、椭圆、双曲线和抛物线等,同时还需关注截面的类型,如平面、柱面和锥面等.2)通过建立合适的空间或平面直角坐标系,结合已知条件建立方程化简得到截面曲线的轨迹方程.

如图2 所示,连接DM,因为DD1⊥平面ABCD,ME⊂平面ABCD,故DD1⊥ME,而D1M⊥ME,DD1∩D1M＝D1,所以ME⊥平面DD1M,而DM⊂平面DD1M,故ME⊥DM.

图2

在平面ABCD中,建立如图3 所示的平面直角坐标系,则A(0,0),B(2,0),C(2,2),D(0,2),E(2,1),因为ME⊥DM,故M在以DE为直径的圆上且圆的方程为

图3

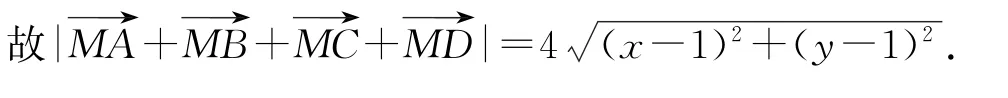
对于空间中动点的轨迹问题,往往需要利用空间中位置关系的判断方法找到平面上动点满足的轨迹方程.本题先考虑M的轨迹,求出轨迹方程,从而把空间问题平面化,再结合该轨迹平面直角坐标系求出的取值范围.

3 借助空间想象能力解决动态问题

空间想象能力是对客观事物的空间形式进行观察、分析和抽象的思维能力.因此,解决动态问题时需要学生具备将形状简单的实物转化为立体几何图形的能力,即将复杂的几何体分解出简单几何体,在简单几何体中找出基本元素及其关系.

例3我国魏晋时期的数学家刘徽创造了一个称为“牟合方盖”的立体图形来推算球的体积.如图4-甲所示,在一个棱长为2a的立方体内作两个互相垂直的内切圆柱,其相交的部分就是牟合方盖.如图4-乙所示,设平行于水平面且与水平面距离为h的平面为α,记平面α截牟合方盖所得截面的面积为S,则函数S＝f(h)的图像是( ).

图4

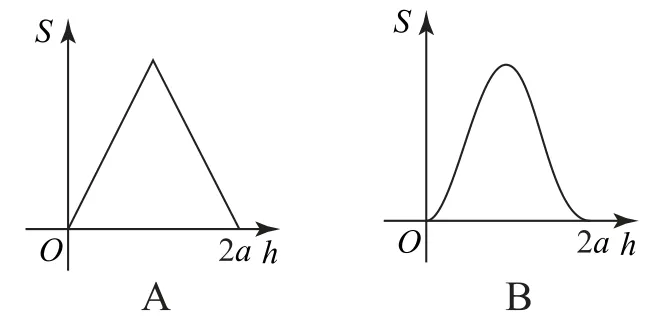
正方体的内切球也是“牟合方盖”内切球,用任意平行于水平面的平面去截“牟合方盖”截面均为正方形,并且此正方形是平面截内切球截面圆的外接正方形,内切球的半径为a,设截面圆的半径为r,则(a-h)2＋r2＝a2,解得r2＝-h2＋2ah.设截面圆的外接正方形的边长为b,则b＝2r,正方形的面积S＝b2＝4r2＝-4h2＋8ah,h∈[0,2a],由函数形式可知,图像应是开口向下的抛物线,故选D.

本题考查了空间想象能力,首先由图4-甲得正方体的内切球也是“牟合方盖”内切球,由图4-乙可知截面均为正方形,此正方形是平面截内切球截面圆的外接正方形,由此计算得到函数解析式,进而求得最终结果.

4 借助向量法解决动态问题

空间向量法适合解决立体几何中的平行、垂直、夹角、距离等问题.此外,空间向量法还适用于解决立体几何中的探索性问题,如:“是否存在”类问题,该类问题经常转化为“点的坐标是否有解,是否在条件限定范围内有解”等,利用向量可以使得问题的解决避免复杂的作图和推理论证等,从而简化求解过程.

例4已知正方体ABCD-A1B1C1D1的棱长为1,点P为其对角面ABC1D1内(含边界)一动点,点P到直线AA1的距离为1,点M,N分别在线段AB,AD1上,且四边形AMPN为矩形,则矩形AMPN面积的最大值为________.

如图5 所示,建立空间直角坐标系,则D(0,0,0),A(1,0,0),B(1,1,0),A__1(1,0,1),D1(0,0,1),则(0,0,1),可设＝(-x,0,x)(0,y,0),x,y∈[0,1],则

图5

本题利用向量法研究点到线的距离,涉及转化思想.首先建立空间直角坐标系,不妨设(-x,y,x),根据点P到直线AA1的距离为1,可得x2＋y2＝1,再根据S矩形AMPN＝AM·AN结合基本不等式即可求出答案.

5 借助函数性质解决动态问题

解决圆锥曲线中的范围或最值问题时,若题目的条件和结论能体现出明确的函数关系,则可先建立目标函数,再求这个函数的最值.利用代数法解决最值与范围问题时常从以下几个方面考虑:

1)利用判别式构造不等关系,从而确定参数的取值范围;2)利用已知参数的范围,求出新参数的范围,解题的关键是建立两个参数之间的等量关系;3)利用基本不等式求出参数的取值范围;4)利用函数值域的求法,确定参数的取值范围.

例5已知椭圆1的左、右焦点分别为F1,F2,经过点F1且倾斜角为θ(0＜θ＜)的直线l与椭圆交于A,B两点(其中点A在x轴上方).如图6所示,将平面xOy沿x轴折叠,使y轴正半轴和x轴所确定的半平面(平面AF1F2)与y轴负半轴和x轴所确定的半平面(平面BF1F2)互相垂直.

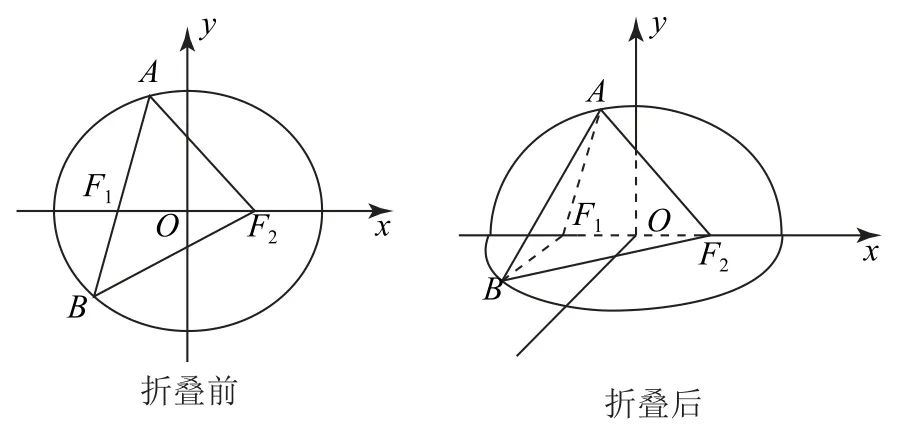
图6

(1)若θ＝,求折叠后|AF1|＋|BF1|-|AB|的值;

(2)求折叠后的线段AB长度的取值范围,并说明理由.

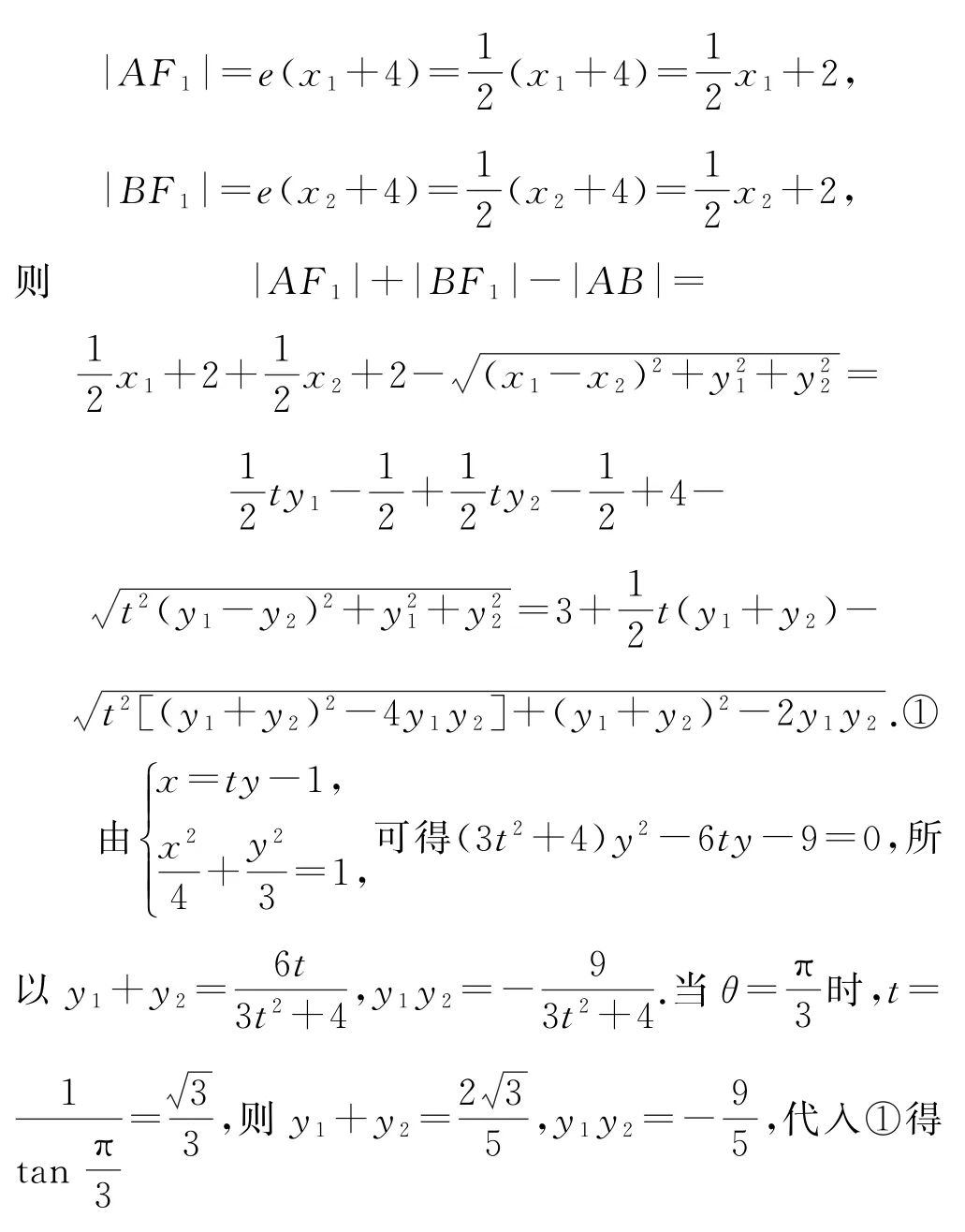
综上,折叠后的线段AB长度的取值范围为

(1)设折叠之前A(x1,y1),B(x2,y2),直线AB的方程为x＝ty-1,与椭圆方程联立可得y1＋y2,y1y2,建立空间直角坐标系,求出A,B,F1三点坐标,结合椭圆的焦半径公式和两点间距离公式将|AF1|＋|BF1|-|AB|表示成关于y1＋y2,y1y2的代数式,代入t得y1＋y2,y1y2的值;(2)结合(1)可将|AB|表示成关于t的函数,t∈(0,＋∞),再利用换元法结合二次函数的单调性即可求解.

6 借助对称性解决动态问题

动态问题中的对称性问题往往涉及点关于点成中心对称,点关于直线成轴对称,曲线关于点、曲线关于直线的中心或轴对称问题等,其中:点关于直线成轴对称问题,该对称轴即为两对称点连线的中垂线,利用“垂直”和“平分”建立方程组即可求解.

例6如图7所示,在长方体ABCD-A1B1C1D1中,|AA1|＝|AD|＝|AB|＝2,E为线段B1C的中点,F是棱C1D1上的动点,若点P为线段BD1上的动点,则|PE|＋|PF|的最小值为______.

图7

如图8 所示,连接BC1,则BC1∩B1C＝E,点P,E,F在平面BC1D1中,且BC1⊥C1D1,|C1D1|＝2,|BC1|＝2,如图8所示.在Rt△BC1D1中,以C1D1为x轴,C1B为y轴,建立平面直角坐标系,如图9所示,则D1(2,0),B(0,2),E(0,1).

图8

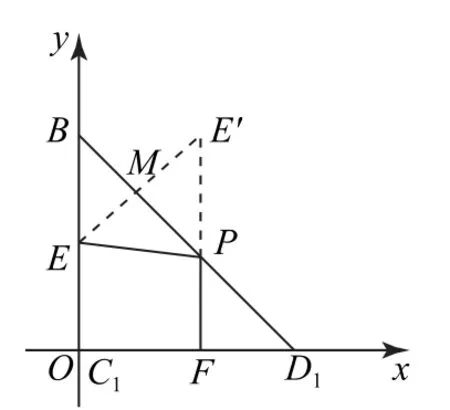
图9

设点E关于直线BD1的对称点为E′,因为BD1的方程为

所以kEE′＝1,直线EE′的方程为

联立①②得x＝,y＝,直线EE′与BD1的交点.对称点E′(1,2),|PE|＋|PF|＝|PE′|＋|PF|≥|E′F|＝2,则|PE|＋|PF|的最小值为2.

首先连接BC1,得出点P,E,F在平面BC1D1中,从而问题转化为在平面内的直线BD1上取一点P,求点P到定点E的距离与到定直线的距离的和的最小值问题,通过建立平面直角坐标系,求出点E关于直线BD1的对称点的坐标.

在立体几何中,关于点、线、面动态问题的试题具有题型多变、综合性较强、涉及知识面较广等特点,需要学生在备考复习过程中加大对高中数学基础知识、基本方法和基本思想的复习力度,重视回顾教材,强化基础知识,剖析知识的本质,挖掘知识的适用情境.

(完)