高考统计试题的考点分析与预测

李智胜 张志强

(山东省淄博市淄博机电工程学校)

高考统计问题多以图表、实际生产生活背景为载体,给出数据,让学生分析和求解相关统计量.本文主要对往年的真题进行分析,并对考查方向进行预测.

1 数据分析

统计试题的考查主要包含两个部分,一是以统计初步为考查对象,对随机抽样、样本的数字特征和统计图表等内容进行考查,有时也可能结合用频率估计概率进行综合考查;二是以统计案例为考查对象,以回归方程和独立性检验为命题内容,这里需要关注非线性回归方程的考查和独立性检验问题的实际意义.若此类问题与概率知识交会命题,则常在解答题中以中低档题出现.

2 考点分析

2.1 统计图表

例1(2021年天津卷4)从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8 组:[66,70),[70,74),…,[94,98),并整理得到如下频率分布直方图(如图1),则评分在区间[82,86)内的影视作品数量是( ).

图1

A.20 B.40 C.64 D.80

由频率分布直方图知,评分在区间[82,86)内的影视作品的频率为(86-82)×0.050＝0.2,故评分在区间[82,86)内的影视作品数量是400×0.2＝80.

对于统计图表问题,要明确图表中数据所代表的意义,要能够分析图表中的数字和图像的走势及实际意义.

2.2 用样本估计总体

例2(2021年全国乙卷理17)某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据,如表1所示.

表1

旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为和

(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).

本题考查了样本特征数的计算,解题的关键是掌握平均数与方差的计算公式,考查的素养主要有数学运算、逻辑推理.

2.3 统计案例

例3(2021年全国甲卷理17)甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如表2所示.

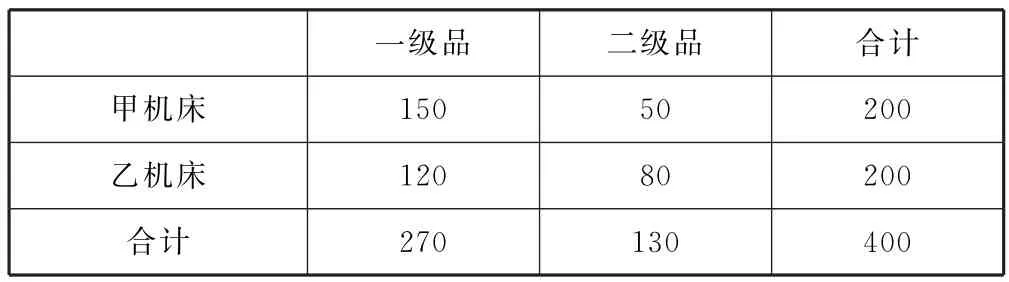
表2

(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?

(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?

表3

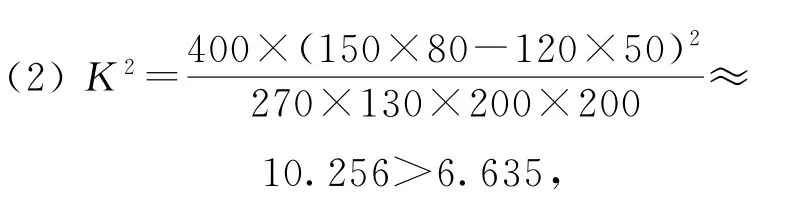
故能有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异.

本题主要考查了频率统计和独立性检验,考查学生的数据分析能力和应用意识,考查的素养主要有数学建模、数据分析.

3 预测练习

1.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图(如图2)和90后从事互联网行业者岗位分布图(如图3,其中90后指1990 年及以后出生,80 后指1980—1989 年之间出生,80前指1979年及以前出生),则下列结论中不一定正确的是( ).

图2

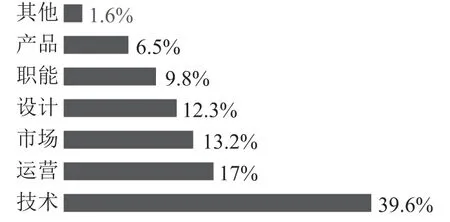
图3

A.互联网行业从业人员中90后占一半以上

B.互联网行业中从事技术岗位的人数90 后比80后多

C.互联网行业中从事设计岗位的人数90 后比80前多

D.互联网行业中从事市场岗位的90后人数不足总人数的10%

答案B.

2.已知数据x1,x2,…,xn的平均数为,方差为s2,则2x1＋3,2x2＋3,…,2xn＋3的平均数和方差分别为( ).

答案B.

通过以上几道例题,相信大家已经对高考统计问题的考查方向有所了解,其实此类问题主要考查学生的计算能力,只要记好公式,掌握规律,按步骤来,一般的问题都能迎刃而解.

(完)