基于小波神经网络的飞行到达时刻预测研究

郑方圆，张光明

（中国民用航空飞行学院，广汉 618307）

0 引言

2020年全年中国民航完成运输总量717.1亿公里，旅客运输量37532.0万人，货邮运输量606.1万吨。在高密度的终端和进近空域，管制员的管制压力随之增强，进而安全隐患也随之增加。因此，基于航迹的运行（trajectory based operation，TBO）应运而生，在TBO的概念下，可以充分利用自动化系统进行航迹运行信息共享，实现空管的精细化运作。根据文献［2］，进场航班的预计到达时间在终端管制空域内起着至关重要的作用。

国内外学者在飞行预计到达时刻的预测主要采用运动学模型和大数据机器学习的方法。顾晓辉等对于直升机的航迹预测建立起灰色预测模型；彭瑛等在研究动态航迹预测算法时，结合了大圆航迹以及等角航迹的实际情况，并用实例验证表明预测误差在0.5分钟内；倪育德等利用ADS-B包含航空器运行的意图信息，将其应用在航迹预测算法的研究中；李阳等采用最小二乘支持向量机（LS-SVM）对历史航迹数据进行训练，建立各轨迹特征与时间的映射关系来进行进场飞行时间的预测；Tastambekov等采用小波分析的方法，将航迹视作函数，对其进行线性回归分析。

基于运动学的模型在建模时过于依赖诸多动力学参数，如大气阻力、风向风速等，这些参数在实际运行中很难精确获取到。在数据机器学习方面，基于本机的历史数据进行回归训练，没有考虑实际突发状况对本机的影响。同时，对于到达时刻的预测，目前的研究多是航迹特征点或重要航路点的过点时间研究，研究条件大多数是在平稳飞行的状况（没有考虑管制员管控、重大天气变化、机动飞行等突发状况）。随着航空器数量的增加，自由航行概念的提出，这对空域内航空器的监视和预测的实时性和精准性都有更高的要求，因此目前来讲仅简单对平稳条件下某些航路点的信息预测是不够的。

针对以上问题，本文考虑到ADS-B数据比传统雷达数据信息种类丰富、获取方便的特点，同时考虑到前机的ADS-B数据能反映当前空域的实际运行状况，将大量的航迹数据应用到神经网络中，用文献提出的系统参数可自适应修正的预测方法，将处理好的ADS-B数据进行网络学习与外推，在实际预测时用同条航路前机的ADS-B数据更新训练数据库，提高预测准确度。

1 航迹数据预分析

1.1 数据特征提取

ADS-B下发数据包括飞机识别信息、ICAO 24位飞机地址码、经纬度、气压/几何高度等。对于本文研究的问题，只考虑以航班号、高度和经纬度为特征的信息数据。因此，对于以时间序列为基础的航迹数据是一个多维向量。假设：

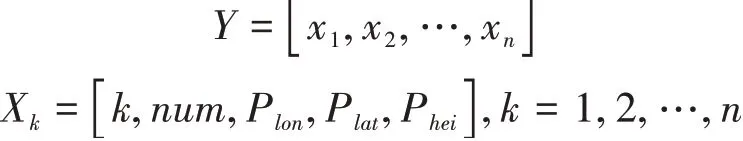
其中，表示过去个时刻航空器的信息时间序列，X表示第时刻航空器的时间、航班号、经度、纬度和高度信息。

1.2 数据预处理

航空器在实际飞行时可能会因为天气影响或设备问题，导致接收机接收到的飞行航机数据往往会出现数据缺失、数据噪声、离群点/异常点，这样的脏数据在投入机器学习模型后会严重影响分析结果和分析效率。因此，补充起飞和降落之间航路点的经纬度，保留航路中线的点迹信息，通过设定阈值，将偏离大的异常数据进行去除。同时由于ADS-B数据发送的时间间隔参差不齐，发送的频率也较高，对于时间间隔小于1 s的数据进行保留，对大于2 s的数据进行差值补充。同时数据采用离差标准化进行归一化处理，统一映射到（0，1）区间，以消除水平数量级差异。

2 基于小波神经网络的飞行ETA预测

2.1 小波神经网络

小波神经网络充分利用小波分析在变换时能够突出问题某些方面的特征，感受奇异点或不连续方向的主要变化，将信号分解为近似部分和特征部分，然后重构该信号。更重要的是，可以在模型中使用尽可能多的点，以提高控制模型的泛化行为。

研究航空器过点时间预测方面使用小波神经网络的优点在于：

（1）和傅里叶变换相比，小波变换在变换时保留了时间信息，即小波变换在时域中拥有分辨能力，这在航迹这种时序数据中尤为重要。

（2）与神经网络理论结合后，小波神经网络算法具备较为理想的函数拟合能力。因为分析时小波分解能够进行平移，因此在理论上能够逼近任意复杂函数函数。

小波神经网络的拓扑图如图1所示。

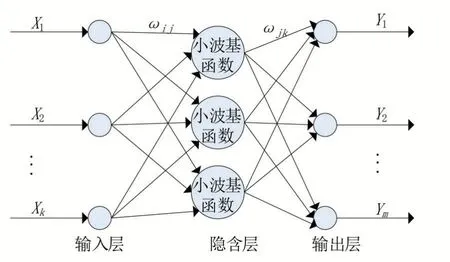
图1 小波神经网络拓扑

其中，，…，X是神经网络的输入，，，…，Y是神经网络的预测输出，ω、ω代表网络的权值。当输入信号序列为x（=1，2，…，）时，输入层的输出为

隐含层的输出为

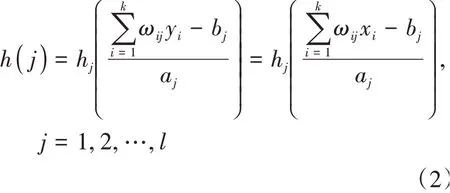
ω为输入层和隐含层的连接权值，b为小波基函数的平移因子，a为小波基函数的伸缩因子，h为小波基函数。本问题采用的小波基函数为Morlet母小波基函数，其公式为

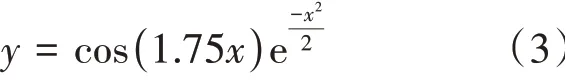
小波神经网络输出层的输出为

式中ω为隐含层到输出层权值，()为第i个隐含层的输出层节点的输出；为隐含层节点数；为输出层节点数。本文将前期得到的数据进行处理，以为采样间隔将航迹进行采样，获得航空器到达每个采样点的时刻。

本文小波神经网络的输入输出参数是：输入为相同航班的历史轨迹采样点的到达时刻、同条航路不同航班的历史轨迹采样点的到达时刻、前机在每个采样点的到达时刻和本机上段航路在每个采样点的到达时刻，输出为本机之后每个采样点相对应的到达时刻。本文的模型结构为3层，由前文的分析可知，航空器的到达时刻预测选用了4个输入参数，因此输入层节点数为4，输出层节点数为1，即输出为航空器的预达时刻，隐含层节点数根据经验公式=++（为输入层节点数，为输出层节点数，为1—10之间的调节因子），比较预测误差将隐含层节点数设为9。

2.2 小波神经网络预测模型构建

研究表明，航空器飞行时某个位置的到达时刻与本航段前几个位置的过点时间有关，并且航班在航路上的过点时间在一定的时间内具有准周期的特性。在一般情况下，航空器的飞行是按照FPL进行的，实际飞出来情况与飞行计划相差不大，但是当面对特殊天气或空域管制时，飞行计划与实际航迹偏差加大，仅依靠历史数据来预测到达时刻是远远不够的。因此，用深度学习的方式挖掘航迹历史数据中和具体的位置、时间没有关系的变化规律。同时，考虑到实时性的需要，将新接收的前机ADS-B数据作为最新预测数据源，实时更新模型，算法流程图如图2所示。

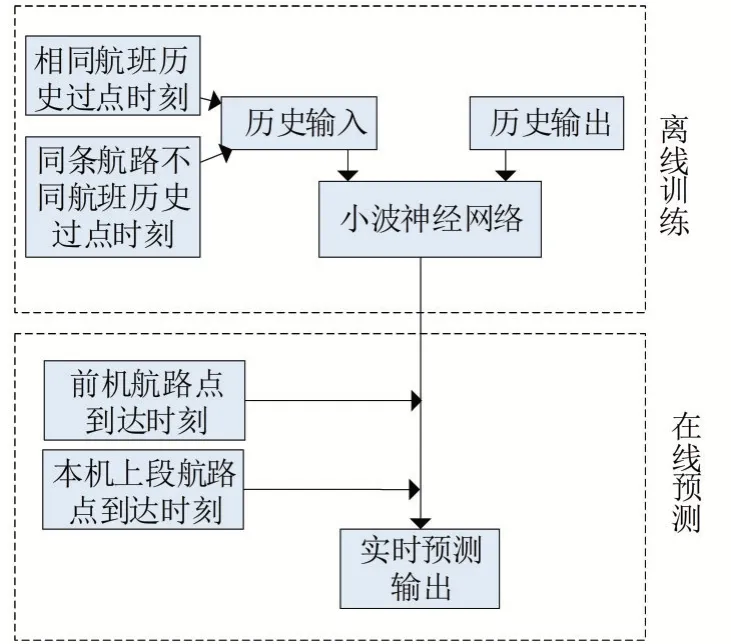
图2 算法流程

3 模拟仿真

3.1 时间预测试验

从FlightAware获取ADS-B数据，该数据是由航路附近ADS-B地面站采集到的。选取某航线进行仿真试验，该航路上涉及的航班有69条航迹数据。其中航迹时长最长的约有110 min，由4400个时刻点组成，平均时间间隔为1.5 s。仿真实验中采集15天的数据，将前14天的数据用于训练，最后一天的数据用于预测。为了反映本文提出的模型的适用性，特意将当天有特殊管制情况的航迹作为测试集数据，该航班15天时间内采集到的每组数据包含航班号、高度、经度和纬度。

本文将预先下载处理好的数据进行预处理，为了降低时间数据处理的复杂性，先将航空器的到达时刻统一转换为时间戳，并对训练的航迹数据进行归一化处理。

基于以上数据，对所构建神经网络使用小波分解方法进行回归预测，所得结果如图3和图4所示。

图3 传统小波神经网络预测结果

图4 传统小波神经网络预测误差

图3中横坐标代时间间隔为1.5 s的不同步长，起点为航空器目前所在位置，纵坐标为到每位置点数据归一化后的时间戳值。图4中横坐标代表每个预测位置点，纵坐标为到达相同位置点时预测值与实际值的误差。从图中可以看出，前85个位置信息的预测性能较好，而在第85个位置点左右时逐渐偏离。分析认为原因是对于时间序列数据，小波神经网络在预测与测试步长过长时，过于滞后的历史数据与最新的运行状况可能有较大差异，用该“老”数据再进行训练预测势必会影响预测精度。

因此本文在原来模型的基础上，添加滑动窗口来进行数据更新，用最新的前机ADS-B数据补充更新数据集，给模型增加了增量学习的功能。在算法的具体实现上，将时序数据划分为独立的时间片段，随着新数据集的增加而向前滑动。

在空-空监视范围上，1090ES为4～50 nmile，雷达管制水平航路间隔为10 km。因此本机最多能接收前方9架航空器的运行数据。以航路间巡航速度大约为800 km/h为例，两机时间间隔至少为45 s。考虑到仅用前方一架航空器的运行数据来判断前方空域状况过于片面化，所以本文同时接收本机前方两架航空器的运行数据，因此观测时间在90 s左右。

而在预测步长和观测点个数的选择方面，本文参考文献［8］和文献［13］，比较观测点个数为10、20、40、60、80，预测步长为20、50、100、200、300时的预测误差，实验结果如表1和表2所示。

表1 观测点数目对误差的影响

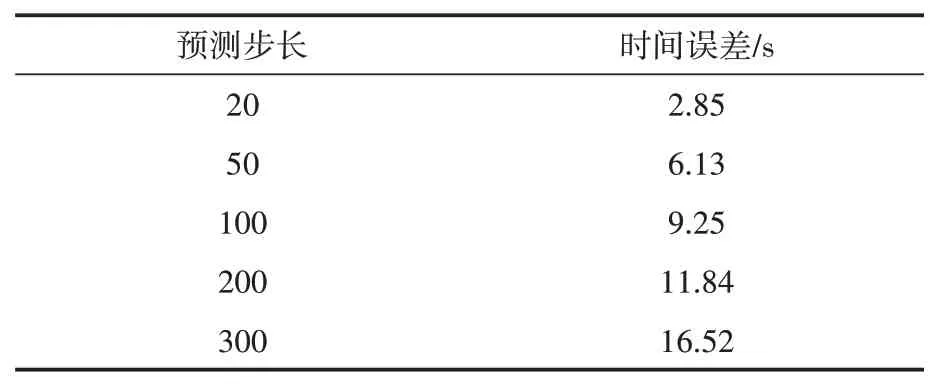
表2 预测步长对误差的影响

由表中数据可知，观测点数目在增加到60个后时间误差基本没有减少，预测步长在5 min时的精度已经较高，并且对于巡航时速在800 km/h的民航客机来说，5 min的航迹相当于66 km左右的航程，这对机组和管制员已经有足够的时间来采取措施进行调整。因此本模型的滑动窗口观测点数为20（30 s），预测步长为200（5 min）。

改进后的模型预测结果如图5—图8所示。其中图5和图6是用滑动窗口改进后bp神经网络的预测结果，图7和图8是用滑动窗口改进后小波神经网络的预测图。从图中可以看出预测值没有出现大的偏离，说明滑动窗口预测改进的有效性。

图5 改进BP神经网络预测

图6 改进BP神经网络预测误差

图7 改进小波神经网络预测

图8 改进小波神经网络预测误差

同时从图中可以看出，在第90个位置点附近，原始数据出现了比较大突变跳跃，原因是可能是当天空管对该空域进行了管制，对于这种情况，从图5中可以看出传统BP神经网络对突变信号不敏感，突变后的初期预测误差较大，不能满足精细化管控的要求。从图7中可以看出，相同情况下小波神经网络敏感地捕获到了突变，并将该信息应用到预测后期数据，突变初期的预测数据与原始数据几乎一致，说明小波神经网络在该问题的适用性。在第170个点附近出现两个值的跳变，分析认为是在实时系统中，并不知道未来的数据是密集的还是缺失的，当数据密集时，数据处理阶段已经完成平均1.5 s时间间隔的过滤，而当数据缺失比较严重时，若没有对数据进行有效插值，时间误差便会比较大。

3.2 预测误差评价指标

为了直观地判断该方法的预测效果，需要为ETA的预测结果选择适当的评价指标，通过比较预测值和实际值的结果，现选用均方根误差（root mean square error，RMSE）和平均绝对误差（mean absolute error，MAE）做评价能更好地对预测的准确性做评价，所得结果如表3所示。

表3 预测时间误差分析

从表中可以看出，改进后小波神经网络的预测均方根误差为19.938 s，平均给绝对误差为14.563 s，预测误差较小。小波算法建立的预测模型能能敏感地捕捉到突变，高效地应用到突发状况时的到达时刻预测。

4 结语

本文基于ADS-B数据采用小波神经网络方法，对航空器的飞行时间进行预测。在代入小波神经网络进行预测前先将得到的位置数据进行预处理。同时考虑到航迹数据为时间序列的特点，采用滑动窗口动态预测的方法，将最新的前方航路运行数据考虑在内，摒弃过于老旧的数据。以某航班为例进行模拟仿真，结果表明改善了预测步长较长时误差变大的问题。同时，小波神经网络在能处理航迹数据突变的情况下，各项预测指标优于BP神经网络，并且预测误差小于现阶段的30 s。但是，本文的数据来源完全是ADS-B提供的航迹数据，没有考虑到气象风的影响，在有大风的情况下，预测经度会大幅度下降，这也将是以后研究的方向和重心。