基于高斯过程的航迹片段关联算法*

2022-09-16郭云飞何苗苗申屠晗

火力与指挥控制 2022年8期

周硕，郭云飞，何苗苗，申屠晗

（杭州电子科技大学自动化学院通信信息传输与融合技术国防重点学科实验室，杭州 310018）

0 引言

在目标跟踪过程中，航迹中断是一个经常发生的问题。航迹中断会使得航迹连续性降低，大量的航迹片段造成传感器存储负担，使得长期跟踪管理不善，进而威胁资源分配，影响传感器跟踪性能。为克服航迹中断带来的挑战，亟需一种能够有效处理中断航迹的方法。

航迹片段关联（track segment association，TSA）方法是一种常见的处理中断航迹的方法。文献［1］最早提出TSA 概念，即通过保持一致的航迹标识来减少中断轨迹的数量并提高整体跟踪器性能。文献［2］提出了一种结合交互式多模型的TSA 方法以提高机动目标航迹的连续性。文献［3］进一步改进TSA 算法，解决了目标停-走情况下的航迹中断问题。针对弹道目标航迹中断的问题，文献［4］提出了一种实时的离散最优TSA 算法。文献［5］对发生航迹中断的场景进行深入研究，提出了目标的类别信息筛选的TSA 方法，将其应用于多普勒盲区下的航迹中断问题。文献［6］进一步考虑新旧航迹的实际终止和起始时间，利用多维分配方法解决航迹片段多义性的问题。

上述TSA 算法都是基于先验模型对目标运动进行预测和回溯，其效果很大程度上依赖于假设的先验模型和未知实际运动模式的匹配程度。当假设的先验模型与实际运动模式不匹配时会导致TSA算法产生较大误差，航迹片段关联正确率下降，关联效果变差。

针对上述问题，提出了一种基于高斯过程的航迹片段关联算法（gaussian process-TSA，GP-TSA）。GP 是基于统计学习理论和贝叶斯理论发展起来的一种机器学习方法。通过在线训练和参数学习，GP 可用于目标跟踪递归预测。在GP 框架下，利用已知航迹片段的量测数据，通过GP 对目标的运动状态函数进行学习，根据学习后的模型对航迹片段进行预测与回溯。在航迹缝合时对于满足关联的新旧航迹，基于航迹片段的先验量测结合GP 将中断区间的预测航迹和回溯航迹融合得到完整航迹。仿真表明，GP-TSA 算法在先验模型与目标实际运动模式不匹配的情况下具有更高的航迹正确率，平均航迹寿命也明显提升。相比于递推缝合方法，所提算法的位置均方根误差更小，且更加平滑。

1 问题描述

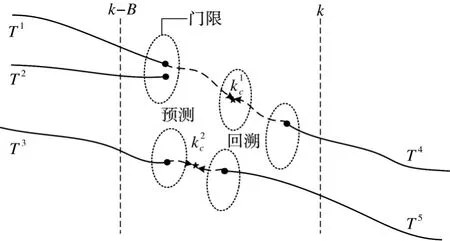
图1 TSA 示意图

对于跟踪器，希望同一个目标从进入探测区域到离开保持一致的航迹标识，而由于目标机动性强、检测概率低、目标被遮挡等原因，在跟踪过程中目标航迹会错误终止或多次起始，即同一目标的航迹标识在有效时间内会产生多个。TSA 算法旨在：1）将源自同一目标的航迹片段关联使航迹标号进行统一。2）将源自同一目标的航迹片段进行缝合得到完整航迹。

2 基于高斯过程的航迹片段关联算法

由于环境的未知影响或随时间的变化，通常会导致先验信息缺失，很难获得精确的运动模型，使传统的TSA 算法正确关联率下降。

本文采用GP-TSA 算法进行航迹片段关联，GP-TSA 算法的流程图如图2 所示。对航迹片段进行分类，将新旧航迹两两组合得到新旧航迹集合。根据初关联得到候选航迹集合。选取关联点，基于GP 分别对旧新航迹进行预测和回溯。经过假设检验对初始候选航迹集合筛选，并通过二维分配算法得到最优新旧航迹集合。基于上述最优解，利用GP融合对中断区间进行缝合获得完整航迹。接下来将介绍GP-TSA 算法的具体步骤。

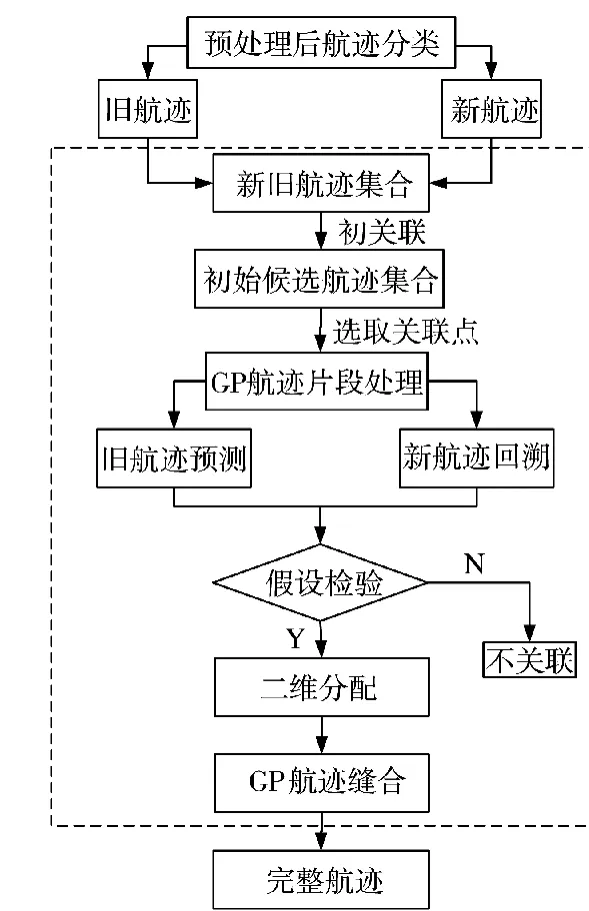
图2 GP-TSA 流程图

2.1 初始候选航迹集合

2.2 高斯过程航迹片段处理

2.2.1 旧航迹的预测

2.2.2 新航迹的回溯

2.3 航迹筛选与配对

在将新旧航迹回溯至k后，引入了二元假设检验的思想，两种假设如下：

2.4 基于高斯过程航迹缝合

根据最优分配结果将关联的航迹对进行航迹缝合。常见的一种缝合方法是将旧航迹预测至k时刻，新航迹回溯至k+1 时刻，从而得到完整航迹。但这种递推的缝合方法会使得到的缝合航迹平滑性较差。本文利用高斯过程融合的方法对中断区间进行缝合，航迹缝合示意图如图3 所示。

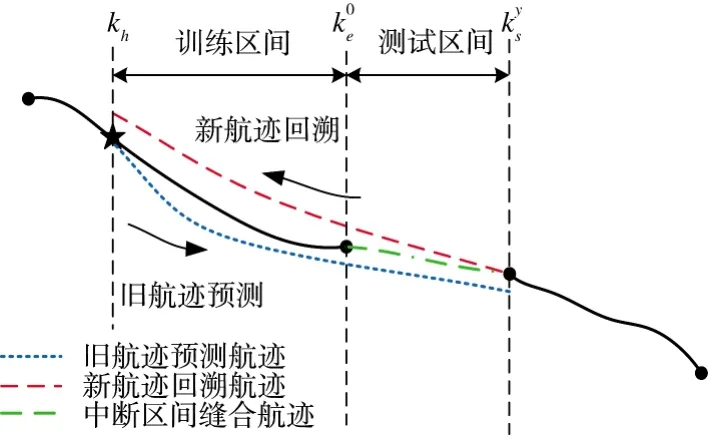
图3 航迹缝合示意图

3 仿真分析

本文设置了两种航迹中断场景，分别利用基于先验模型的TSA 方法和GP-TSA 方法进行航迹片段关联，并在同等条件下对中断航迹运用不同方法进行缝合。通过分析航迹关联正确率、平均航迹寿命和位置均方根误差，验证了GP-TSA 算法的有效性。

3.1 仿真评估指标

本文采取以下性能指标对所提算法进行评估。

1）平均正确关联率r：

其中，n为目标正确关联的数目；M为蒙特卡洛次数。

2）总航迹寿命（total track life，TTL）：

其中，l为同一个目标的航迹片段长度；l目标寿命长度。

3）平均航迹寿命（mean track life，MTL）

其中，n是航迹片段数目。

此外假设航迹片段需要满足：雷达采样间隔为T=1 s，且每个航迹片段至少包括6 个点迹。

3.2 仿真分析

3.2.1 场景1

假设雷达静止，且位于（0 m，0 m），在3 000 m×3 000 m 的探测区域内存在8 个目标，表2 给出了目标初始状态。

表1 文中常见符号及意义

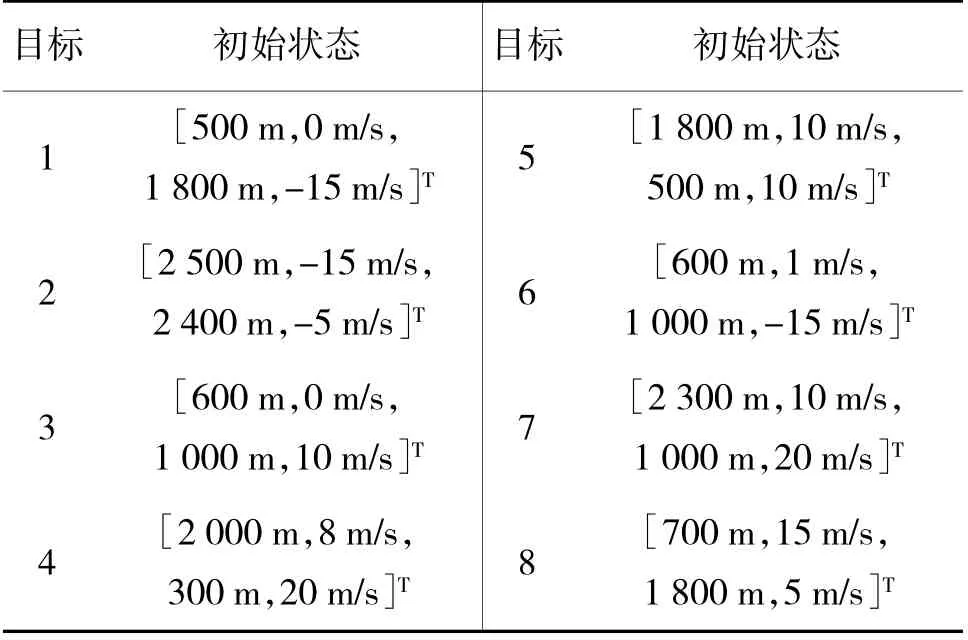
表2 场景1 目标初始状态

图4 为场景1 仿真结束后的航迹片段图。从图中可以看出，由于过程噪声较大，导致实际目标运动轨迹并不完全符合标准的CV 运动模型，在没有进行TSA 处理的情况下雷达共观测到12 条航迹片段，各航迹片段的起始时刻（其中，k表示起始时间，k表示终止时间）如表3 所示。经过50 次蒙特卡洛后，统计不同算法的正确关联率及MTL 情况。

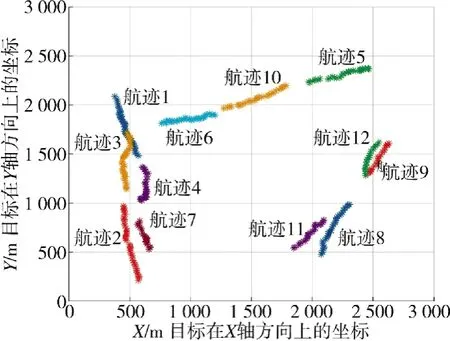
图4 场景1 航迹片段图

表3 场景1 下航迹起止时间表（s）

图5 为GP-TSA 处理后的航迹片段关联结果。从图中可以看到，通过GP-TSA 能够有效的将同一目标的航迹片段关联进行关联。结合图4 可以得到，实际发生航迹中断的是目标1、目标2、目标3和目标4，计算可以得到目标1～4 的平均TTL 分别为0.826、0.793、0.822、0.797。

图5 场景1 GP-TSA 的关联效果图

综合表4、表5 可以得到，在场景1 下，CV-TSA算法和GP-TSA 算法的航迹正确关联率和MTL 明显高于CV-TSA1 算法。这是由于CV-TSA 算法，其先验模型及噪声与实际运动模相匹配，而GP-TSA算法的关联效果与先验模型无关，因此，两种算法都能够达到减少航迹片段数量，提高航迹寿命的效果。在利用CV-TSA1 算法进行航迹片段关联处理时，目标2 和目标4 的运动模式与CV 模型匹配程度较高，关联效果较好，而目标1 和目标3 的运动模式与标准CV 模型匹配程度有一定的偏差，因此，再进行航迹片段处理时会产生较大偏差，进而影响航迹片段的关联效果，导致目标平均正确关联率较低。统计GP-TSA 算法单次耗时为5.037 s，CV-TSA算法和CV-TSA1 算法单次耗时分别为2.931 s 和3.101 s。由于GP-TSA 算法需要进行数据训练，因此，耗时略大于CV-TSA 方法。

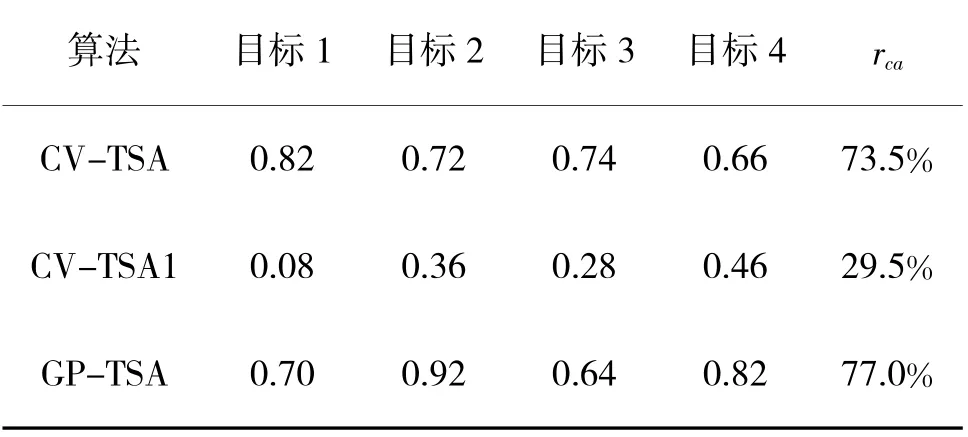
表4 不同算法正确关联率统计

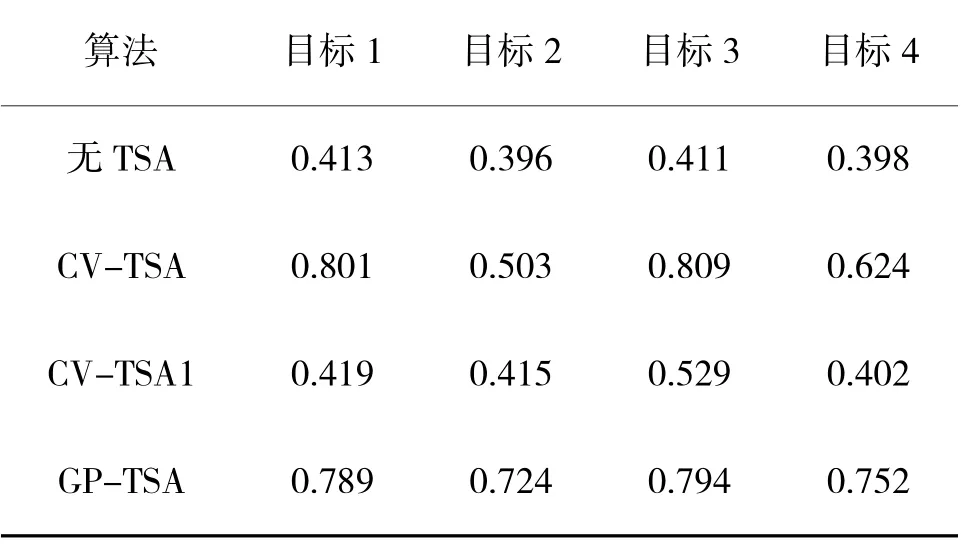
表5 不同算法下目标的MTL 统计

表6 为50 次蒙特卡洛后，根据递推缝合的航迹和基于GP 融合的缝合航迹的位置均方根误差（root mean square error，RMSE）。从表中可以看出，GP-TSA 算法相比于将新旧航迹预测至中点缝合航迹的方法位置RMSE 更小，能够有效地将中断航迹进行缝合得到完整航迹，从而提高了航迹的连续性。

表6 目标中断处缝合航迹位置RMSE（m）

3.2.2 场景2

假设雷达静止，且位于（0 m，0 m），在3 000 m×3 000 m 的探测区域内存在9 目标，表7 给出了目标初始状态。目标在仿真时间N=100 s 内均作ω=0.5°的匀速转弯（constant turn，CT）运动。航迹中断时间主要发生在42 s～65 s。其他参数与场景1 相同。分别利用先验模型为CV，Q=diag（［5 m，0.001 m/s，5 m，0.001 m/s］）的TSA 算法（记CV-TSA3）和GP-TSA算法进行航迹片段关联处理。

表7 场景2 目标初始运动状态

图6 为目标在场景2 下未进行TSA 算法时雷达观测到的航迹片段图。从图中可以看出，目标运动结束时共产生了14 个航迹片段，雷达实际观测到的各航迹的起止时间如表8 所示。结合图7 可以看出实际发生中断的目标为目标1～5，其TTL 分别为0.639、0.769、0.648、0.616、0.759。

表8 场景2 下航迹的起止时刻（s）

图6 场景2 航迹片段图

图7 为场景2 下GP-TSA 算法处理后的航迹关联效果图。经过GP-TSA 处理后，由目标产生的航迹片段均已正确关联，结合图6 可以看出，实际发生中断的目标为目标1、目标2、目标3、目标4、目标5，通过计算可以得到发生中断的5 个目标的TTL 分别为0.639、0.769、0.648、0.616、0.759。

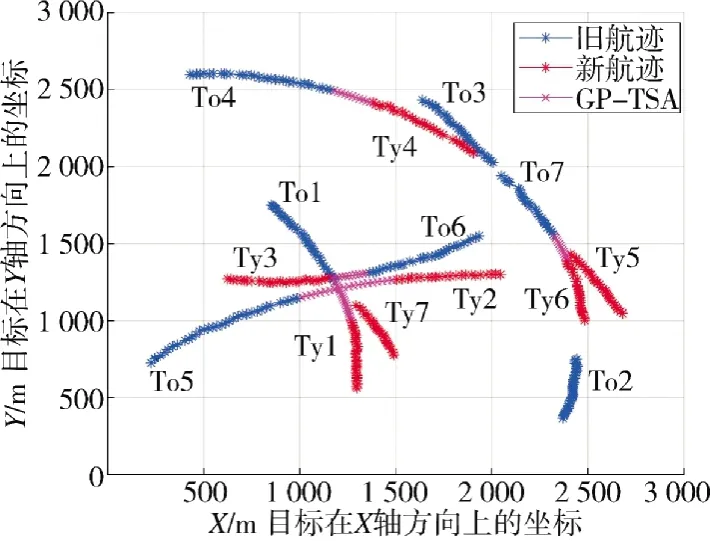
图7 场景2 GP-TSA 的关联效果图

从表9 中可以看出，GP-TSA 算法处理后的单个目标的航迹关联正确率和平均关联正确率均明显高于CV-TSA 算法。表10 的MTL 统计情况看出相比于没有TSA 处理时，GP-TSA 算法在场景2 下能够有效的提高航迹的MTL，而CV-TSA 算法对于目标MTL 几乎没有明显的改善效果。

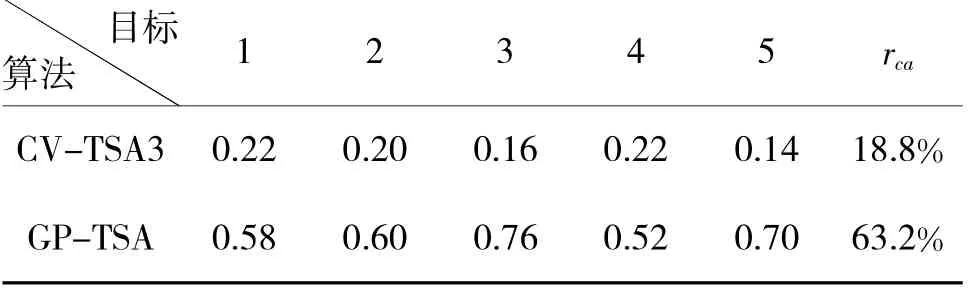
表9 场景2 两种算法正确关联率统计

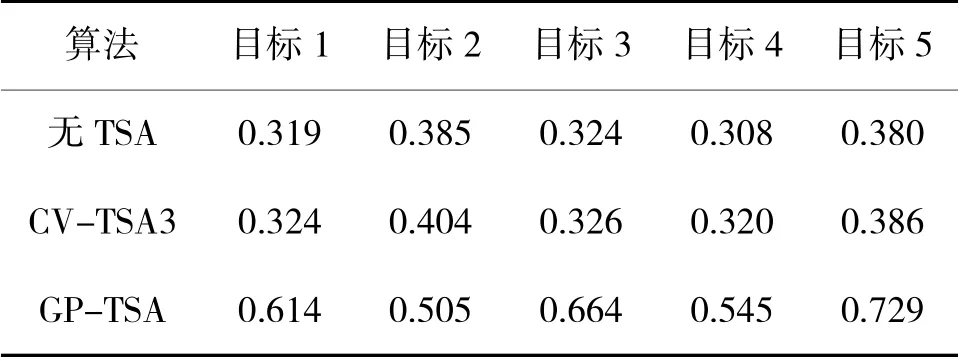
表10 场景2 不同算法MTL 统计

综上所述，在场景2 下GP-TSA 算法能够有效对航迹片段进行关联处理，提高航迹的平均寿命，且整体关联效果优于CV-TSA 算法。这是由于目标实际的运动模型为CT，而进行TSA 处理时假设先验模型为CV，在利用CV-TSA 算法处理航迹片段时产生的偏差较大，会使得目标的航迹片段与虚假航迹关联，从而导致关联错误或关联失败。而GP-TSA 算法则是通过航迹片段的量测数据进行训练学习，不受目标运动模式的影响，在场景2 下的航迹片段关联效果更好。