RNP离场程序航路点优化方法研究

任思潜，张光明

（中国民用航空飞行学院飞行技术学院，广汉 618307）

0 引言

近年来，所需导航性能（required navigation performance，RNP）已经广泛应用于我国越来越多的机场，特别是用于导航精度较高的机场。随着我国民航运输业高速发展，空中交通流量急剧增加，导致终端区有限空域资源与极速增长空中交通流量之间的矛盾不断地加大，这不仅增大了航空公司运营成本，也造成了大量航班的延误。因此，在满足航空器安全运行的前提下，合理地规划终端区空域以及优化RNP离场程序对于提高终端区运行效率、节省飞行时间和缩短飞行距离具有很大意义。

目前，有关终端区飞行程序设计与优化，国内外已经有不少学者专家对其进行相关研究，并都提出了相应可参考的优化方法，南京航空航天大学钱戈等，从飞行程序设计所要求的安全性、经济性、简便性及噪声影响四个方面构建了多目标的飞行程序优化模型，并运用改进的多目标蚁群算法对其求解，实现对终端区空域合理科学地规划。上海华东民航飞行程序设计研究院左凌等，对飞行程序设计的限制因素和设计要求两方面进行着重分析，为飞行程序设计提供了一种技术方法。中国民用航空飞行学院黄邦菊等，通过运用三次样条插值法对复杂地形机场仿真以及使用一种改进的A*算法对云南普洱机场4条离场程序分别进行设计研究，为复杂地形机场离场程序设计提供了一种方法。但是，关于针对航路点布局及航路点特征对仪表离场程序优化问题相关研究却很少。严伟、王瑛等通过考虑几种不确定因素对北京飞行情报区航路网络建立多目标优化模型，并采用粒子群优化（PSO）算法对其求解，解决了航路网络的运行成本与安全性之间冲突矛盾问题，实现了情报区航路网航路点布局优化，但未涉及到针对终端区IFP航路点布局的研究。

针对现有基于航路点的RNP离场程序优化研究较少的现状，本文以某机场离场程序为例，以跑道末端上方15 ft位置为起始点，以离场结束位置为终点，在起始点和终点之间搜寻一条最优标称航迹，将其作为该离场方向的最优飞行程序并与原有飞行程序做对比，研究航路点对飞行距离影响。具体研究思路为：首先给出了规划区域障碍物评估原则以及航路点选取方法，在此基础之上，根据规章规定相关限制要求构建终端区离场程序优化方法；再者，针对某机场离场程序提出了一种优化方案，并采用遗传算法（Genetic Algorithm，GA）对其进行求解，最后通过实验对比优化前后的飞行程序。

1 规划区域障碍物评估原则

判定障碍物是否在保护区区域内是进行仪表离场程序优化的首要步骤，其中保护区区域分为多边形区域与圆形区域。其次，在判定之后，还需对保护区内障碍物进行越障评估，并计算新的程序设计梯度（PDG）。

1.1 障碍物在多边形区域

若保护区区域为多边形形状，则研究考虑使用射线法进行判定，其核心思想是以任意一个障碍物作为起点，朝着某一个水平方向作一条射线，计算该射线与多边形的交点个数，如果为奇数则障碍物在多边形区域内，反之，不在则表示在多边形区域外。

1.2 障碍物在圆形区域

若障碍物区域为圆形形状，则计算当前障碍物与该圆形区域中心的距离是否小于半径。

保护区内障碍物评估分为直线保护区障碍物评估和转弯保护区障碍物评估，障碍物评估方法如下。

1.2.1 直线保护区

假设该保护区内存在一障碍物，高米，位于中线右侧米，且其投影在标称航迹上距离跑道末端米。

判定障碍物是否穿透障碍物鉴别面（OIS）计算式如式（1）所示。

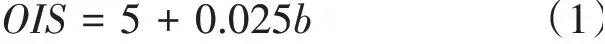
式（1）中，若计算得OIS值小于，则判定该障碍物未穿透，反之则穿透。如果穿透OIS面，则对该障碍物进行超障计算，方法如下。

最低超障高计算表达式如式（2）所示、

RH值计算如式（3）所示。

根据式（3）得到的RH值计算新的PDG值。如式（4）所示。式（4）中，为障碍物至跑道末端水平距离。

1.2.2 转弯保护区

本文中，考虑的是在指定高度转弯的情形。该情形下转弯保护区内最小超障余度计算方法采用的是K-K线法。

不考虑H类直升机，规章规定，K-K线前障碍物最小超障高度应满足表达式（5）。

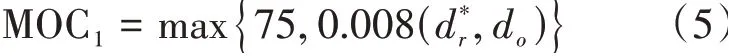
K-K线后障碍物最小超障高度应满足表达式（6）。

式（6）中，d 表示从DER至K-K线的水平距离；d 表示从转弯起始区边界至障碍物的最短距离。

根据式（5）和式（6）则得该转弯保护区内允许的最小超障高如式（7）所示。

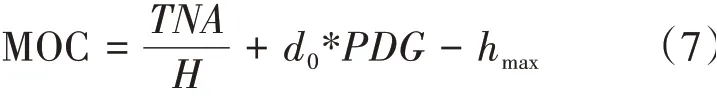
式（7）中，为指定高度处转弯高；为最高的障碍物标高。

1.3 最短稳定距离航路点选取准则

传统飞行程序由于受到障碍物及地形的限制，且其保护区范围随着航空器与导航台间距离增加而增加，因此，相对于传统飞行程序的航路点来说，PBN飞行程序中的航路点与其存在一定差异，即只要是处在信号的有效覆盖区域内，就可自由灵活的设置航路点位置。

本文考虑采用最短稳定距离（MSD）来选取航路点，具体方法是以MSD为半径，以当前位置为圆心确定圆周，在该圆周上选定一个点作为前方航路点并再将其作为圆心，依次类似选取前方航路点。

2 离场飞行程序优化方法

后续离场程序优化模型构建过程中，都必须满足于以下假设条件。

（1）待优化飞行程序起始点与终点位置均已知。

（2）不考虑飞行限制区，只考虑保护区内越障要求。

（3）不考虑ATC管制特殊要求。

（4）不考虑H类直升机。

2.1 地理信息网格化

离场程序设计前，需对机场地图数据进行预处理。以机场ARP点为中心将其120 km半径区域进行网格化，将2度跨度近似地划分为7202×7202网格，显然网格精度间隔取6.73e-10 rad。

××机场（ARP点坐标：E109°42'19″,N27°26'38″）为例划分，结果如图1所示。

图1 ××机场120km半径区域

由于数字高程DEM的存储和计算机矩阵的存储是沿中线上下翻转对称，因此，在使用之前需预处理。如图2所示是DEM数字地形存储位与计算机存储位关系。

图2 ××机场数字地形存储方式

通过等距采样625个点位置及高程信息形成25×25的采样矩阵，并结合邻近样条插值法对某机场120范围内三维地形进行还原，还原得到地形如图3所示。

图3 ××机场三维地形地貌图

2.2 优化约束条件

根据航空器运行目视和仪表飞行程序设计规范及民用航空器性能限制要求，在构建离场程序优化数学模型时，需考虑航空器最低飞行高度、IFP航段保护区、最短航段距离、最大转弯角度、最大转弯离场角度及最大爬升梯度等约束条件。

2.2.1 最低飞行高度

在对离场程序进行设计或优化过程中，航空器需满足规章所规定的最低飞行要求。即航空器最低飞行高度与障碍物高度差值必须大于最小超障余度，如式（8）所示。

式（8）中，表示航迹上任意一点所对应的飞行高度；表示障碍物实际高度；示航迹上任意一点所需满足的最小超障余度。

2.2.2 IFP航段保护区

式（9）中，点表示航迹上任意一点；示航空器飞行在某一点上最大偏移值；表示航迹上某一点处对应的保护区半宽。

2.2.3 最短航段距离

当航路点属性为Fly by时，此时该航段的最短距离应满足式（10）。

式（10）中，表示航路点转弯所需的MSD。

当航路点属性为Fly over时，此时该航段的最短距离应满足式（11）。

式（11）中，表示航路点转弯所需的MSD。

2.2.4 最大转弯角度

转弯角度表示的是下一航段相对上一航段偏转角，在理论上，其取值范围介于0°～180°之间，如式（12）所示。

2.2.5 最大转弯离场角度

航空器性能限制其在起飞离场时爬升至某一高度，再转弯加入离场航线的最大角度，如式（13）所示。

2.2.6 最大爬升梯度

根据规定，离场程序设计时，航空器爬升梯度不应超过10%，如式（14）是航空器爬升梯度约束表达。

式（14）中，Δ表示航迹上前后两点之间的高度差，即h-h；表示航空器从前一航迹点至后一航迹点之间的水平距离。

2.3 优化目标函数

在飞行程序优化过程中，优先考虑安全余量最大作为优化目标，在满足安全余量最大情形下，再分别考虑航空器飞行距离最短、航路点个数最少以及转弯次数最少作为次优化目标，目标函数如式（16）—式（18）。

2.3.1 安全余量最大

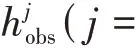
根据式（15），可得航迹相对障碍物最大安全余量和目标表达式如式（16）。

2.3.2 飞行距离

2.3.3 航路点个数最少

在起始点至终点之间采取逐个添加航路点方法。假设从起点至终点之间可取=(=1,2,3,…)个航路点，按最短稳定距离将个航路点分别划分至K个阶段，然后分别求解=取值时，在K阶段下满足最短飞行距离及越障要求的航路点。

2.3.4 飞行路径平滑程度

在进行飞行程序优化时，应减少飞行转弯次数，尽量保证航空器直线飞行。针对此，如式（18）给出了飞行路径平滑程度评价表达式。

2.4 优化仿真流程

运用上述构建的离场飞行程序优化方法，借助于遗传算法，沿大圆航线对原有飞行程序进行寻优改进。

2.4.1 染色体编码

在这里，是将遗传算法中的染色体看作空间中的一个航路点，即一个染色体对应一个航路点。显然，若染色体个数越多，航路点的个数也越多，则最后搜寻得到航迹就越接近于理论上最优解。

在生物进化过程中，生物DNA存在4种碱基对，DNA上4种碱基对的不同排列方式则表示不同的DNA编码，从而导致基因的表现出来的性状不同。同理，在计算机就算过程中，模仿生物DNA编码方式，将0、1两种取值看作两种不同碱基对，由0、1两种碱基对构成的不同的二进制字符串则可表示不同实数。

2.4.2 个体

个体表示的是航路点，也表示一个染色体，且计算机求解过程中将其编码为一串由0、1二进制数构成的向量。

2.4.3 种群及种群初始化

种群表示的是个体的集合，在这里则代表所有航路点集合。

种群的初始化是可行区域中满足约束条件下所有可能的航路点集合。在本文计算中，种群初始大小取值为50。

2.4.4 适应度计算与选择

选择的主要目的是将通过种群初始化得到种群利用给定的适应度规则把优秀个体保留下来，即就是通过适应度值选择出最佳的航路点。在这里，适应度值是以飞行距离、安全余量及飞行路径平滑程度作为评价指标，并进行加权得到个体选择适应度函数，如式（19）所示。

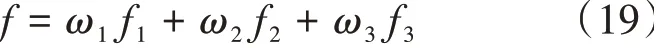
式（19）中，权重、、均是根据具体需求给定，其中计算所得适应度值越大越好。

确定每个个体适应度值后，根据式（20）计算每个个体相对适应度，该值用于估计个体被保留下来的概率。

式（20）中，=1，2，…，，表示初始化后种群个体数。

2.4.5 交叉和变异

经过选择得到了当前看来最符合的航路点，但这有可能并不是最优的。为防止出现局部最优情况，需通过生物进化繁殖后代即交叉与变异过程来不断地更新产生比当前更优的个体。

交叉操作是将两个个体的染色体上的基因型进行交换，在这里，即就是将航路点、、坐标序列进行两两互换。而变异操作就是改变某个个体的染色体上的基因。也就是将航路点、、坐标取值用另一个数值替代。一般来说，交叉概率值通常取0.8，变异概率值通常取0.005。

最后，多次反复进行选择、交叉、变异这一过程，迭代出最优个体，即找到当前最优的航路点，并将航路点连接起来，即可获得从起始点至终点的一条最优飞行路径。

3 仿真实验与结果分析

图4表示××机场××跑道一条离场程序，航空器沿040°方向从跑道末端起飞，飞越CJ411航路点至CJ505航路点，然后再按航路点P167、P159、LLC顺序飞行，至离场结束位置。

图4 ××跑道××离场程序

优化前的××跑道××离场程序如图5所示。

图5 优化前××离场飞行路径

仿真条件：假设航空器此次最大转弯角度为75°；最大爬升梯度为4.8%，且梯度为均匀增加；路径搜索过程中最大迭代次数为5500次。优化后飞行路径如图6所示。

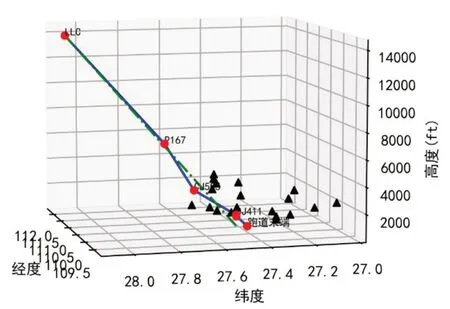
图6 优化后飞行路径

从起点至终点沿大圆航迹距离为137.85 NM，相比优化前程序，航图距离减少了9.37 NM，安全余量增加了0.13 NM，航路点个数减少了1个。优化前后飞行路径距离及安全余量对比如表1所列。

表1 优化前后飞行程序对比

4 结语

本文在不考虑飞行限制区和ATC管制要求的前提下，对某机场现有飞行程序进行优化改进，仿真结果可以看出，在满足约束条件情形下，本文提出的离场程序优化方法可以实现从跑道末端至离场结束时的飞行路径规划，并且规划后的结果相比原有飞行程序路径更加平直、飞行距离更短、安全余量更大。