剖析线性化处理后的化学平衡常数与温度关系
2022-04-21晏雄
晏雄
(湖南省浏阳市第一中学)
1 问题的提出
化学反应原理中最核心的物理量是化学平衡常数,可用来定量描述可逆反应的程度.化学平衡常数只受温度影响,由于升高温度平衡向吸热反应方向移动,故升高温度吸热反应的平衡常数增大,放热反应的平衡常数减小.
其实化学平衡常数与温度也存在定量关系,由范特霍夫等温方程ΔG=ΔG⊖+RTlnK⊖与吉布斯-亥姆霍兹方程ΔG⊖=ΔH-TΔS可知,平衡时ΔG=0,即有RTlnK⊖=-ΔH+TΔS,两边同除以T变形可得RlnK⊖=-+ΔS,假定ΔS不受温度影响,可视为常数(K⊖为相对分压表示的平衡常数).在高考试题中常以信息形式给出lnK⊖或lgK⊖与的线性关系,或者给出线性方程:
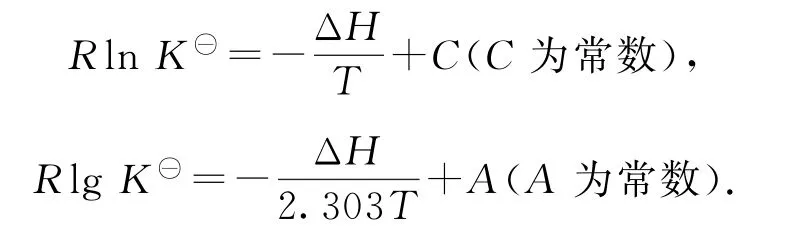
如果将K⊖换成分压表示的平衡常数Kp或物质的量分数表示的平衡常数Kx,也依然存在线性关系.这类试题信息量大,对数理逻辑能力要求较高.
2 由线性方程判断ΔH 的符号与相对大小
例1(2021 年广东卷,有删改)我国力争于2030年前做到碳达峰,2060年前实现碳中和.CH4与CO2重整是CO2利用的研究热点之一.该重整反应体系主要涉及以下反应:
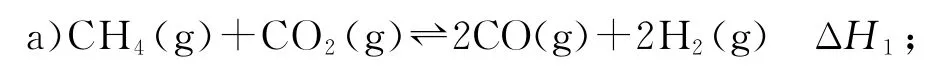

设为相对压力平衡常数,其表达式写法:在浓度平衡常数表达式中,用相对分压代替浓度.气体的相对分压等于其分压(单位为kPa)除以p0(p0=100kPa).反应a、c、e的ln(温度的倒数)的变化如图1 所示.反应a、c、e中,属于吸热反应的有_________(填字母).

图1
分析①随着温度的升高减小,反应a和c的ln增大,说明的数值增大,反应向正反应方向进行,反应a和c为吸热反应,同理反应e的ln减小,说明减小,反应向逆反应方向进行,反应e为放热反应,故属于吸热反应的有ac.
如果给出的是线性方程:
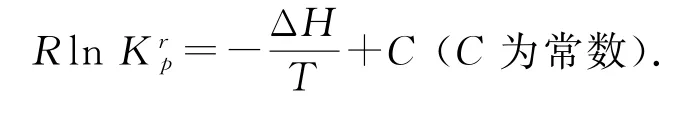
由直线方程可知-ΔH/R为该直线的斜率,直线单调递增ΔH<0,直线单调递减ΔH>0,直线越陡|ΔH|越大,反应a、c、e中e为放热反应,a、c为吸热反应,3个反应的ΔH大小为a>c>0>e.
3 由线性方程计算ΔH
例2(2021年八省联考湖南卷,有删改)氨基甲酸铵(H2NCOONH4)为尿素生产过程的中间产物,易分解:H2NCOONH4(s)⇌2NH3(g)+CO2(g).
已知:RlnKp=-+C(C为常数).根据实验数据得到图像(如图2-甲),则该反应的反应热ΔH=________kJ·mol-1.

图2
分析由直线方程可知-ΔH为该直线的斜率,直线下降,斜率为负值,即ΔH>0,为吸热反应;或升高温度,减小,横坐标往左移动,纵坐标值RlnKp增大,即Kp增大,升高温度平衡常数增大,故反应为吸热反应(ΔH>0).由直线上任意两点的坐标可求出斜率如图2-乙所示,先找出Δy与Δx再进行计算:

4 由线性关系综合分析ΔH
如果信息不足,只给出线性关系而不给线性方程,就只能判断ΔH的符号而不能判断ΔH的相对大小,需要根据其他条件综合分析ΔH.
例3(2021年山东卷,有删改)2-甲氧基-2-甲基丁烷(TAME)常用作汽油添加剂.在催化剂作用下,可通过甲醇与烯烃的液相反应制得,体系中同时存在如下反应.

反应Ⅰ、Ⅱ、Ⅲ以物质的量分数表示的平衡常数Kx与温度T变化关系如图3所示.据图3判断,A 和B中相对稳定的是_________(填符号);的数值范围是________(填标号).
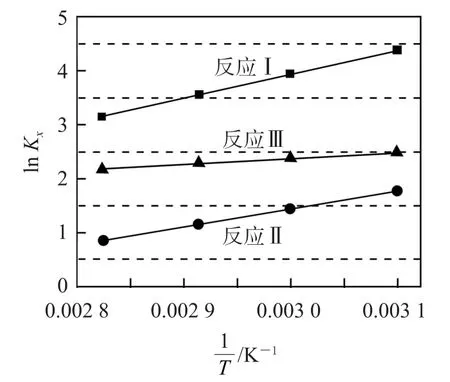
图3
A.<-1 B.-1~0
C.0~1 D.>1
分析如果给出了线性方程可根据斜率直接得出:ΔH1<ΔH2<ΔH3<0.由lnKx与的线性关系图可知,3个反应在升高温度时,减小,横坐标往左移动,纵坐标lnKx值均减小,即Kx减小,升高温度平衡常数减小,故3个反应都为放热反应(ΔH<0),由反应Ⅲ可知,A 的能量高于B,故相对稳定的是B.又由盖斯定律可知,反应Ⅱ与反应Ⅲ相加可得反应Ⅰ,则ΔH1=ΔH2+ΔH3,因此ΔH1<ΔH2<0,由于放热反应的ΔH越小,其绝对值越大,则的数值范围是大于1,答案为D.
例4(2021 年全国乙卷,有删改)一氯化碘(ICl)是一种卤素互化物,具有强氧化性,可与金属直接反应,也可用作有机合成中的碘化剂.一定条件下发生分解反应:2ICl(g)=Cl2(g)+I2(g).McMorris测定和计算了在136~180 ℃范围内下列反应的平衡常数Kp.
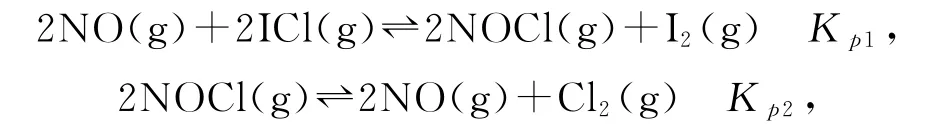
得到lgKp1~和lgKp2~均为线性关系,如图4所示.
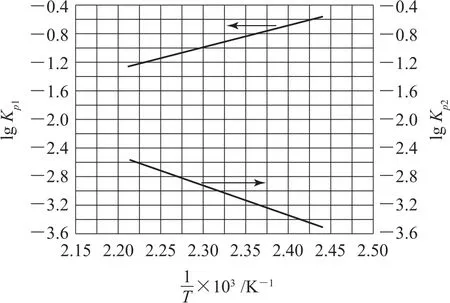
图4
①由图可知,NOCl分解为NO 和Cl2反应的ΔH_________0(填“大于”或“小于”).
②反 应2ICl(g)=Cl2(g)+I2(g)的K=________(用Kp1、Kp2表示):该反应的ΔH0(填“大于”或“小于”),写出推理过程_________.

高考中要解答好这类试题,需要学生有较强的数理推理能力,须结合直线的单调性、斜率、截距等,应用已有的反应热ΔH与平衡常数K相关概念的内涵与外延进行定量计算,再运用计算结果进行证据推理解决实际问题,这些都需要深度探究与思考如何进行模型认知与证据推理,因此提升数理逻辑能力是培养化学学科核心素养必由之路.
(完)
