用角平分线定理找有界磁场轨迹圆圆心

杨天才

(重庆市高新区教师进修学院)

1 问题的提出

求有界磁场的最小范围问题,对学生的平面几何知识与物理知识的综合运用能力要求较高.其难点在于带电粒子进入有界磁场后一般只运动一段圆弧后就飞出磁场边界,其运动过程中的临界点(如运动形式的转折点、轨迹的切点、磁场的边界点等)难以确定,如何确定轨迹圆弧的圆心就成了解题关键.笔者发现借助角平分线定理(角平分线上的点到这个角两边的距离相等),通过尺规作图可轻松确定圆心的位置,使问题得以简化.该方法的应用依据是已知初、末速度所在的直线,则所有轨迹圆的圆心均在初、末速度所在的直线延长线(或反向延长线)相交所成夹角的角平分线上.如果还知道下列某一条件,圆心就能进一步确定了:1)轨道半径大小;2)入射点;3)出射点.如表1所示.

表1

2 实例分析

2.1 已知轨道半径

例1如图1所示,在倾角为30°的斜面OA的左侧有一竖直挡板,其上有一小孔P,OP＝0.5m.现有一质量m＝4×10－20kg,带电荷量q＝＋2×10－14C 的粒子,从小孔以速度v0＝3×104m·s－1水平射向磁感应强度B＝0.2 T、方向垂直纸面向外的一圆形磁场区域,且在飞出磁场区域后能垂直打在OA面上,粒子重力不计.

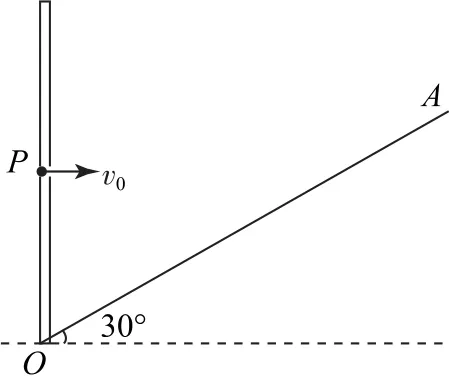
图1

(1)求粒子在磁场中圆周运动的半径;

(2)求粒子在磁场中运动的时间;

(3)求圆形磁场区域的最小面积;

(4)若磁场区域为正三角形且磁场方向垂直纸面向里,粒子运动过程中始终不碰到竖直挡板,其他条件不变,求此正三角形磁场区域的最小面积;

(5)若磁场区域为矩形且磁场方向垂直纸面向里,粒子运动过程中始终不碰到竖直挡板,其他条件不变,求此矩形磁场区域的最小面积.

解析

(2)已知入射方向垂直挡板,出射方向垂直斜面,将入射方向延长,出射方向反向延长,二者相交成一角度,角平分线上到两速度所在直线距离等于半径的点即为圆心,画出粒子运动的某个轨迹如图2所示,由几何知识得轨迹对应的圆心角θ＝60°,又T＝,则粒子在磁场中运动的时间

图2

(3)显然,当粒子的轨迹圆直径正好是PQ时,圆形磁场区域的半径最小,根据几何知识知PQ＝r,由数学知识可得圆形磁场区域的最小半径R＝＝0.15m,最小面积S1＝πR2＝2.25×10－2·πm2.

(4)已知入射方向垂直挡板,出射方向与挡板相切,所以圆心O1在过P点与水平方向成45°角的射线上,在射线上取到挡板距离等于半径的点为O1(圆心),画出粒子的运动轨迹如图3所示,由数学知识可得三角形的边长L＝,得

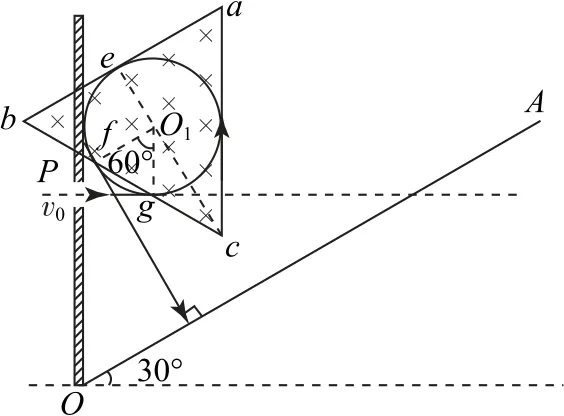
图3

(5)与上一问类似,画出粒子的运动轨迹如图4 所示,矩形的长x＝2r＝0.6 m,宽y＝r＋rcos30°＝,所以面积

图4

点评

这道题中粒子运动轨迹和磁场边界临界点的确定比较困难,必须将入射速度方向与从OA边射出速度的反向延长线相交,根据运动半径已知的特点,在夹角平分线上找圆心,画运动轨迹.另外,在计算最小边长时一定要注意圆周运动的轨迹并不是三角形磁场的内切圆.

2.2 已知入射点

例2一质量为m、带电量为＋q的粒子以速度v0从O点沿y轴正方向射入磁感应强度为B的一圆形匀强磁场区域,磁场方向垂直于纸面,粒子飞出磁场区后,从b处穿过x轴,速度方向与x轴正向夹角为30°,如图5 所示(粒子重力不计).

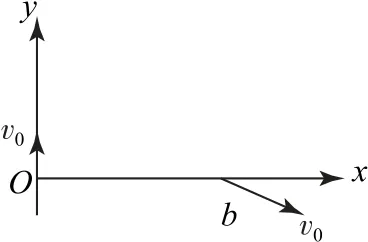
图5

(1)求圆形磁场区的最小面积;

(2)求粒子从O点进入磁场区到达b点所经历的时间;

(3)求b点的坐标;

(4)若磁场区域为矩形且磁场方向垂直纸面向外,其他条件不变,求此矩形磁场区域的最小面积;

(5)若磁场区域为正三角形且磁场方向垂直纸面向外,其他条件不变,求此正三角形磁场区域的最小面积.

解析

(1)由题可知,粒子不可能直接由O点经半个圆周偏转到b点,其必在圆周运动不到半圈时离开磁场区域后沿直线运动到b点.可知,其离开磁场时的临界点与O点都在圆周上,到圆心的距离必相等.如图6所示,过b点逆着速度v0的方向作虚线,与y轴相交,由于粒子在磁场中偏转的半径一定,且圆心位于x轴上,作夹角的平分线与x轴交于O1,O1点即为圆周运动的圆心,则圆的半径R＝OO1＝O1a.由qv0B＝,得R＝.弦长Oa为l＝,要使圆形磁场区域面积最小,半径应为l的一半,如图6所示,即,面积

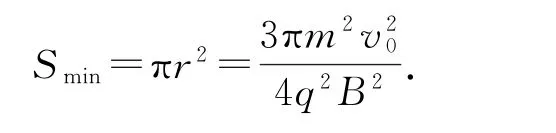
图6

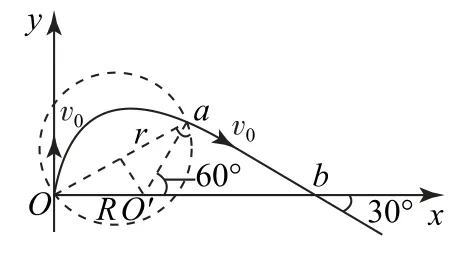
图7

(4)若为矩形磁场,要使矩形磁场区域面积最小,则轨迹圆半径的一半刚好为矩形磁场的宽,弦长Oa刚好为矩形磁场的长,那么其面积为

(5)若为正三角形磁场,要使磁场区域面积最小,则轨迹直径应为正三角形磁场的边长,那么其面积为

点评

此题关键是找到圆心和粒子射入、射出磁场边界的临界点,注意圆心必在两临界点速度垂线的交点上且圆心到这两临界点的距离相等;还要明确所求最小圆形磁场的直径等于粒子运动轨迹的弦长,最小矩形磁场的长边等于粒子运动轨迹的弦长,最小正三角形磁场的边长等于粒子运动轨迹的弦长.

2.3 已知出射点

例3如图8 所示,直角坐标系xOy第一象限的区域存在沿y轴正方向的匀强电场.现有一质量为m,电荷量为e的电子从第一象限的某点P(L,),以初速度v0沿x轴的负方向开始运动,经过x轴上的点进入第四象限,先做匀速直线运动,然后进入垂直纸面的矩形匀强磁场区域,磁场左边界和上边界分别与y轴、x轴重合,电子偏转后恰好经过坐标原点O,并沿y轴的正方向运动,不计电子的重力.

图8

(1)求电子经过Q点的速度v;

(2)求该匀强磁场的磁感应强度B和磁场的最小面积S;

(3)若磁场区域为圆形,其他条件不变,求此圆形磁场区域的最小面积;

(4)若磁场区域为正三角形,其他条件不变,求此正三角形磁场区域的最小面积.

(2)如图9所示,电子以与x轴负方向成30°角进入第四象限后先沿QM做匀速直线运动,然后进入匀强磁场区域做匀速圆周运动.恰好以沿y轴向上的速度经过O点.过Q点延长速度所在的直线,与y轴负半轴相交,夹角的角平分线与x轴相交于O′点,以O′为圆心作半圆与过Q点的速度延长线相切于M点(M点即为磁场的边界点),弧MNO即为粒子在矩形磁场中运动的轨迹,所以磁场的右边界和下边界就确定了.显然O′点到O点的距离与到直线QM上M点的垂直距离相等且为轨迹圆的半径,设偏转半径为,由图9可知＝3R,解得B＝,方向垂直纸面向里.矩形磁场的长度LOC＝,宽度,矩形磁场的最小面积

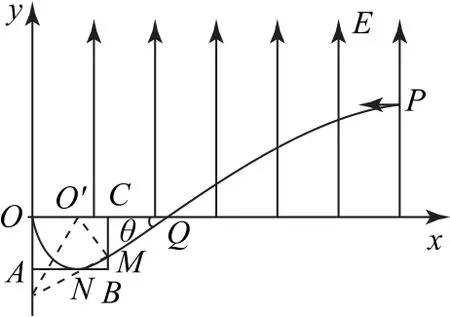
图9

(4)同理,若为正三角形磁场,则正三角形磁场区域面积最小时边长为弦长OM,其面积为

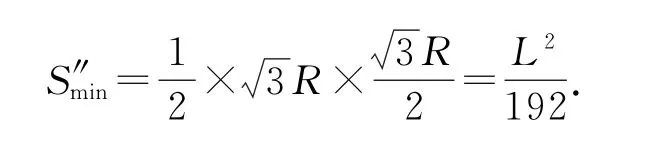
小结解决带电粒子在磁场中运动的问题,一般有两条思路:一是平面几何法,即先根据平面几何知识,利用尺规作图画出粒子的运动轨迹,其他问题自然迎刃而解.对于如何画出粒子的运动轨迹,本文探讨了如果已知入射方向和出射方向所在的直线,可先将两直线延长(或反向延长)相交,确定圆心在其夹角的平分线上,再根据其他条件画圆的方法.二是解析几何法,如果不能确定粒子的具体运动轨迹,可以先假设轨迹圆的存在,然后利用代数的方法,逐步推证轨迹圆满足的规律直至求解.

(完)