“平抛运动”典型考点例析
2022-04-21任东超
任东超
(安徽省濉溪县第二中学)
“平抛运动”是高考的重点内容之一,在历年考试中都有考查,因此也是一个常考考点.“平抛运动”试题要求学生在牛顿运动定律的基础上结合运动的合成与分解思想进行思考,并熟练掌握从一维向二维的情境转换,因此也是考试的难点之一.论题型,其在高考选择题、实验题和计算题三种题型中都有出现,若单独考查该知识点,通常作为选择题出现,试题难度一般不大;若出现在实验题或计算题中,则通常属于中高难度题.
1 基础知识归纳
1)定义:物体只在重力作用下,初速度沿水平方向的运动.
2)特点:a)平抛运动是物体同时经历水平方向的匀速直线运动和竖直方向的自由落体运动的合运动.b)平抛运动的轨迹可用表达式y=ax2+bx+c表示,因此是一条抛物线.c)平抛运动在竖直方向上的分运动的加速度为g(类平抛运动加速度不为g)且恒定,匀加速直线运动的所有公式都适用.
3)重要推论:a)在同一时刻,平抛运动的速度(与水平方向的夹角为α)方向和位移方向(与水平方向的夹角为θ)是不同的,且满足关系式tanα=2tanθ(如图1).b)任意时刻速度的延长线必交于此时物体位移的水平分量的中点(如图中B点为OC的中点).

图1
4)常见类型:单体平抛、多体平抛、类平抛、斜抛等,其中后两者难度相对较大.
5)常用解题思路:a)利用速度分解求解;b)利用位移分解求解;c)利用运动的对称性和可逆性求解.
2 常见类型例析
2.1 单体平抛类型
一个物体以一定的初速度被水平抛出,如果除其自身重力外其他力可忽略不计,则这个物体所做的运动就是典型的平抛运动.对这个物体进行分析,需要结合运动的分解思想:水平方向上的匀速直线运动和竖直方向上的自由落体运动.这就是开篇所提到的“从一维向二维的情境转换”.掌握了以上知识,再应用分运动的相应规律和推论,就能够轻松解题了.
例1小明是一名跳台滑雪爱好者,他为了能够更好地欣赏北京冬奥会比赛,结合自己所学的物理知识对跳台滑雪进行了一些研究.他将跳台滑雪运动抽象为一个在斜坡上的平抛运动.如图2所示,当滑雪运动员从助滑道滑出瞬间,认为其初速度v0的方向为水平向右,着陆坡为倾角为θ的斜面,运动员最终落到M点.若测得点O、M的距离为s,运动员在空中运动的时间为t,则下列选项中,有关s、t和v0的关系正确的是().
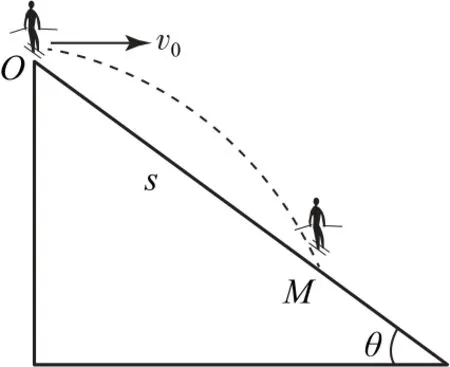
图2

解析
本题属于结合实际问题对平抛运动最简单直接的考查,解题关键是“运动的分解”.平抛运动的“分解”涉及位移的分解和速度的分解,由于本题运动的起点和终点已经明确,故利用位移的分解即可快速解题.

点评
平抛运动的两个重要推论:1)做平抛运动的物体在任一时刻、任一位置处,其末速度和水平方向的夹角α与位移和水平方向的夹角θ,满足关系tanα=2tanθ;2)做平抛运动的物体在任一时刻的瞬时速度方向的反向延长线一定通过此时水平位移的中点.
2.2 多体平抛类型
多体平抛属于综合性题目,相对于上面的单一的平抛运动,多体平抛题型中又增加了数个研究对象和新的运动形式,通常会与竖直上抛、匀变速直线运动相结合,解题的关键是要对多个研究对象作出正确的分析,并找到不同运动在时间、位移、速度等方面的内在联系.
例2(多选)如图3所示,在水平地面上方h处有小球A和B,它们之间的距离为l.若将小球A以速度v水平向右抛出,同时将小球B由静止释放,且知道两个小球在与水平地面碰撞后竖直分速度方向相反而大小不变.忽略空气阻力和碰撞时间,下列说法正确的有().

图3
A.A、B一定能相碰
B.A、B不可能运动到最高处相碰
C.A、B在第一次落地前若不碰,此后就不会相碰
D.A、B在第一次落地前能否相碰,取决于A的初速度
解析
本题学生容易错选C 而漏选D,究其原因是对小球A、B在运动方面的内在联系分析不准确.根据题意,我们可以发现,在竖直方向上两个小球其实是同步运动的,水平方向上,可认为B球不动,A球匀速向B球靠近.因此两个小球一定能相碰,且可能在B球运动到最高处相碰.
由题意可知,小球A做平抛运动,小球B做自由落体运动.对小球A的运动进行分解可知,其在水平方向做匀速直线运动,在竖直方向做自由落体运动;因此两个小球在与地面碰撞前运动时间t1相同,且.若第一次落地前相碰,只要满足A运动时间,选项D 正确;因为A、B在竖直方向的运动同步,始终处于同一高度,且A与地面相碰后水平速度不变,所以A一定会经过B所在的竖直线与B相碰,碰撞位置由A球的初速度决定,选项B、C错误,选项A 正确.
点评
1)若将两物体同时抛出,且抛出时的高度相同或处在同一点,则运动过程中两物体的高度始终相等,两物体的距离只由水平分运动决定;2)若抛出时两物体存在高度差,则在物体落地之前两物体的高度差始终不变,两物体的间距由水平分运动和高度差决定;3)若两物体从同一点不同时刻抛出,两物体间的高度差随时间匀速增大,两物体的间距由两物体的水平分运动和竖直分运动决定.
2.3 类平抛运动类型
类平抛运动可以看作物体在与初速度方向垂直的恒定合外力作用下所做的曲线运动.类平抛运动的轨迹仍然是抛物线,分析方法也跟平抛运动类似,其与平抛运动的最大区别在于垂直初速度方向上的分运动(注意,类平抛运动的初速度方向未必是水平的).我们可以将类平抛运动分解为沿初速度方向上的匀速直线运动和垂直于初速度方向上的初速度为0的匀加速直线运动.
类平抛运动问题的求解思路:根据物体受力特点和运动特点判断该问题属于类平抛运动问题→求出物体运动的加速度→根据平抛运动知识,结合具体问题选择所需要的规律.
例3如图4 所示,在一个与水平面夹角为θ的光滑斜面的端点上,将两个可视为质点的小球A、B以相同的速度v水平抛出,其中小球A在竖直平面内运动,落在水平面的点P1处;小球B在斜面上运动,落在水平面的点P2处.若空气阻力忽略不计,下列选项中判断正确的是().
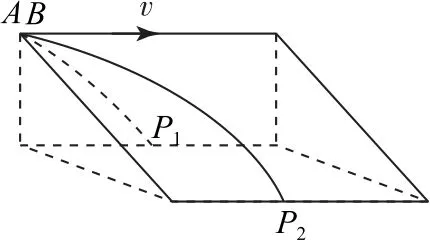
图4
A.小球A、B运动的时间相同,但水平方向上的位移不同
B.小球A、B运动的时间不同,且水平方向上的位移不同
C.小球A、B沿水平方向上的位移相同
D.小球A、B的运动时间相同
解析
由题意可知小球A做平抛运动,设其运动时间为t1,水平运动位移为x1,竖直运动位移为h,则有x1=vt,h=.小球B在斜面上的运动为类平抛运动,可将其运动分解为沿水平方向的匀速直线运动和沿斜面的匀加速直线运动,设其运动时间为t2,水平运动位移为x2,由几何知识可知小球B沿斜面的加速度为g·sinθ,运动位移为,则有.因为t1≠t2,所以x1≠x2.故选项B正确,选项A、C、D 错误.
点评
确认研究对象做类平抛运动的条件是研究对象受恒定外力作用且力的方向与初速度方向垂直.解决类平抛运动的问题完全可以按照平抛运动来处理,即将运动分解为两个方向的运动,其中垂直初速度方向的运动是初速度为0的匀加速直线运动.
2.4 斜抛运动类型
斜抛运动是指以与水平方向成一定角度的初速度将物体斜向上抛出,物体在只受重力作用下所做的曲线运动.斜抛运动是匀变速曲线运动,其加速度为g.初速度与水平方向的夹角叫抛射角.解决斜抛运动,除了运动的分解外,还可以利用运动的对称性进行分析.
例4小明是一个运动健将,尤其擅长立定跳远.在一次立定跳远中,测得他离开地面时的速度方向与水平地面的夹角为θ,距离地面的最大高度为h,跳出的成绩为5h,若不计空气阻力,小明可被看作质点,求tanθ的值.
解析
按照题意可作出小明立定跳远的运动示意图如图5 所示,其中A点为起跳点,B点为最高点,整个运动过程可分为对称的两部分.做平抛(或类平抛)运动的物体在任一时刻任一位置处,设其末速度方向与水平方向的夹角为θ,位移与水平方向的夹角为α,则tanθ=2tanα,由几何知识可得tanα=,得tanθ=2tanα=0.8.

图5
点评
斜抛运动最大的特点是对称性和可逆性.就如例4所示,小明的运动可从最高点B处分成两个除方向不同其他均相同的平抛运动.另外,斜抛运动中能达到的最高点和水平位移的大小与初速度和抛射角都有关,且存在规律:当初速度不变时,抛射角等于45°时,水平位移有最大值.
(完)
