例析解决“关联速度”模型的几种方法

胡东明 周尧

(湖北省武汉市新洲区第一中学(阳逻校区))

所谓关联速度模型,就是两个物体通过绳、杆或直接接触发生联系,求两物体速度之间的关系.解决问题的基本方法是微元法,即两物体在相同的极小时间内发生极小位移,由于绳、杆不可伸长,或直接接触的物体不可形变,两物体沿绳、杆或垂直于接触面方向的分位移相同,即分速度相同.在微元法的基础上,还可以衍变出效果分解法、瞬时功率法、相对运动法等方法,这些研究方法适用于经典物理学中一般绳、杆和刚体模型.通过对此类问题的研究,可以加深对运动的合成与分解方法的理解.下面举例分析.

1 绳连接物体模型

用轻绳连接的两物体,将两物体的速度沿绳方向和垂直于绳方向正交分解,由于轻绳不可伸长,两物体沿绳方向速度相同.

例1如图1 所示,某人站在岸上通过绕过定滑轮的绳子向岸边拉船,他拉绳子的速率v不变,当拉船的绳子与水平面成θ角时,船前进的速度u为多大?

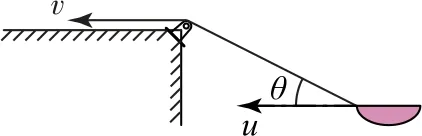
图1

解析

解法1效果分解法

将船的速度u沿绳和垂直于绳两个方向正交分解,沿绳方向的分速度与人拉绳的速度相同,即ucosθ＝v,解得u＝.

点评

为什么要将船的速度正交分解?船有沿绳斜向上运动和垂直于绳绕定滑轮的接触点转动的效果.以绳与定滑轮的接触点为参照物,船在沿绳方向的分速度与绳的速度相同,另一分速度使船绕接触点顺时针旋转,即垂直于绳方向.

解法2微元法

如图2,取极短的时间Δt,在这一小段时间内,人和船的速度都不变,船从A运动到B,位移为Δx＝uΔt,绳拉过的位移为Δl＝vΔt.这个运动可设想为由两个分运动合成:小船先被绳拉过Δl到C点,再随绳绕滑轮O点做圆周运动到B点.在OA上取OC＝OB,则AC＝Δl,由于时间Δt极短,∠BOC趋近于零.

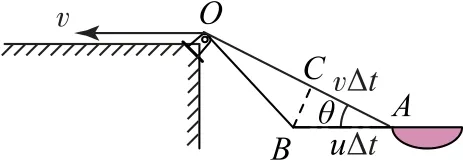
图2

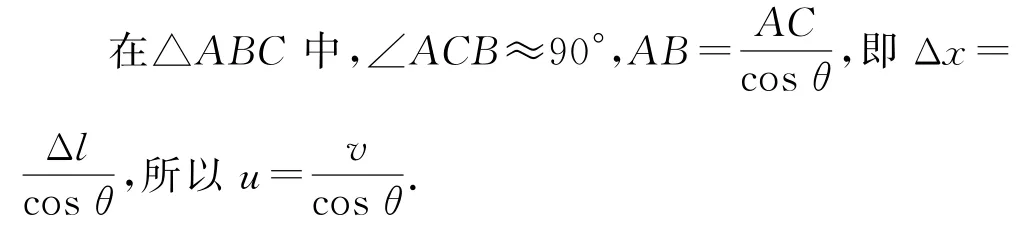
点评

微元法很有说服力,能让学生从运动的角度很好地理解船速与绳速的关系.

解法3瞬时功率法

从能量的角度理解,绳既不会提供能量,也不会消耗能量,即绳两端弹力的瞬时功率大小相等.设人对绳的拉力和绳对船的拉力大小均为T,人对绳的拉力的瞬时功率大小为P1＝Tv,绳对船的拉力的瞬时功率大小为P2＝Tucosθ,由P1＝P2可解得u＝.

点评

根据能量守恒,绳或杆连接体间相互作用力的瞬时功率相等.如果中间是用弹簧或橡皮筋连接,由于有弹性势能变化,两端连接体间的相互作用力的瞬时功率就不相等了.

例2如图3 所示,悬线一端固定在天花板上的O点,另一端穿过一张光盘的中央小孔后拴着一个小球,小球静止时,竖直悬线刚好挨着水平桌面的边缘.现将光盘按在桌面上,并沿桌面边缘以速度v匀速移动,移动过程中,光盘中央小孔始终紧挨桌面边缘,当悬线与竖直方向的夹角为θ时,小球移动的速度大小为().

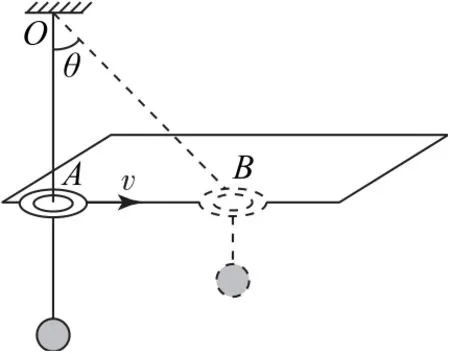
图3

解析

解法1效果分解法

光盘有沿悬线方向斜向下运动和垂直于悬线绕O点转动的效果.将光盘水平向右移动的速度v分解为沿悬线方向的速度和垂直于悬线方向的速度,而小球上升的速度大小与光盘沿悬线方向斜向下的分速度大小相等,为vsinθ,故小球的运动速度大小为,故选项A 正确.

解法2微元法

如图4 所示,取极短的时间Δt,在这一小段时间内,光盘和小球的速度都不变,光盘从B点运动到C点,位移为Δx＝vΔt,在OC上取OD＝OB,则小球上升的位移为Δl＝uΔt,u为小球竖直方向的分速度,且CD＝Δl,由于时间Δt极短,∠BOD趋近于零,∠BCD趋近于90°－θ.

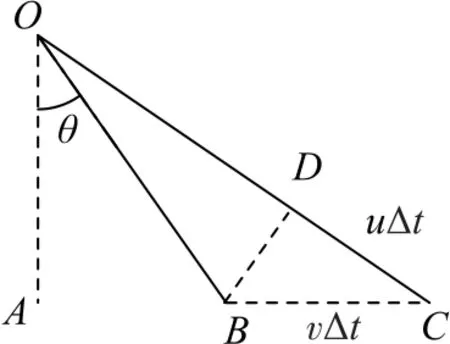
图4

在△BCD中,∠BDC≈90°,CD＝BCcos(90°－θ),即u＝vsinθ.

小球在水平方向与光盘同步,速度为v,故小球的实际速度为水平方向速度v与竖直方向速度u的合成,即为,故选项A正确.

点评

微元法虽然复杂些,但是能将原理分析得清清楚楚,注意本题只分析出了小球竖直方向的分速度u.由于小球合速度方向不容易分析,因此,本题用瞬时功率法求解难度较大.

例3(多选)(2013年上海卷)如图5为在平静海面上,两艘拖船A、B拖着驳船C运动的示意图.A、B的速度分别沿着缆绳CA、CB方向,A、B、C不在一条直线上.由于缆绳不可伸长,因此C的速度在CA、CB方向的投影分别与A、B的速度相等,由此可知C的().

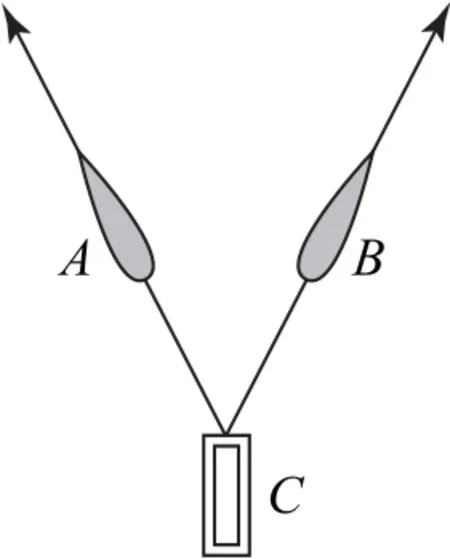
图5

A.速度大小可以介于A、B的速度大小之间

B.速度大小一定不小于A、B的速度大小

C.速度方向可能在CA和CB的夹角范围外

D.速度方向一定在CA和CB的夹角范围内

解析

将C的速度沿CA方向和垂直于CA方向正交分解,根据C的速度在CA、CB方向的投影分别与A、B的速度相等可知,C的速度沿CA方向的分速度等于A的速度,所以C的速度大小一定大于A的速度大小;同样的,将C的速度沿CB方向和垂直于CB方向正交分解,可知C的速度大小一定大于B的速度大小.故选项A 错误,选项B正确.若C的速度方向在CA和CB的夹角范围外,如图6-甲所示,将C的速度沿CA方向及垂直于CA方向正交分解,也可以如图6-乙所示,将C的速度沿CB方向及垂直于CB方向正交分解,这两种分解都是满足题意的,故C的速度方向可能在CA和CB的夹角范围内,也可能在CA和CB的夹角范围外,故选项C正确,选项D 错误.

图6

点评

有同学想当然地认为将C的速度沿两绳方向分解,这是不对的.根据微元法分析可知,这里只能正交分解,即C速度应该分别沿着两绳的方向和垂直于两绳的方向分解,这是因为从效果上看,C既有沿CA运动和垂直于CA运动的效果,又有沿CB运动和垂直于CB运动的效果,这就是效果分解法.

2 杆连接物体模型

用轻杆连接的两物体,将两物体的速度沿杆方向和垂直于杆方向正交分解,由于轻杆不可伸长,两物体沿杆方向速度相同,垂直于杆方向角速度相同.

例4如图7所示,一轻杆连接两个小球A和B(可视为质点),在一竖直直角形墙角开始运动,当杆与竖直墙壁的夹角为θ时,球B的速度大小为vB,求此时球A的速度大小vA.

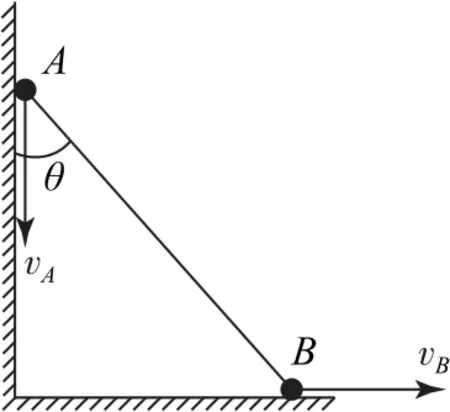
图7

解析

解法1效果分解法

小球A、B分别具有沿杆运动和垂直于杆转动的效果.将vA、vB均沿杆和垂直杆方向分解,由图8知两球沿杆方向速度大小相等,即vAcosθ＝vBsinθ,得vA＝vBtanθ.

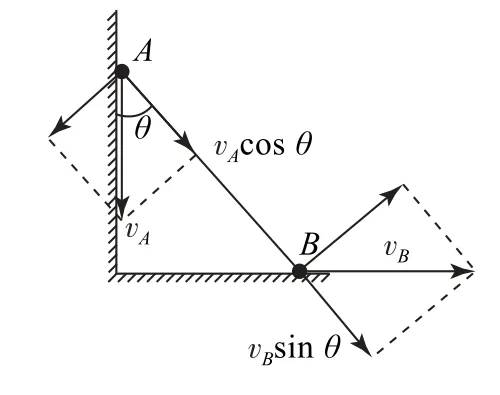
图8

解法2相对运动法

以球B为参考系,即假定B球静止,则A球绕B球做圆周运动.将A球的速度vA沿vB的方向和垂直于杆方向分解如图9所示,其沿vB方向的分速度与vB相同,由矢量图可知,vA＝vBtanθ.

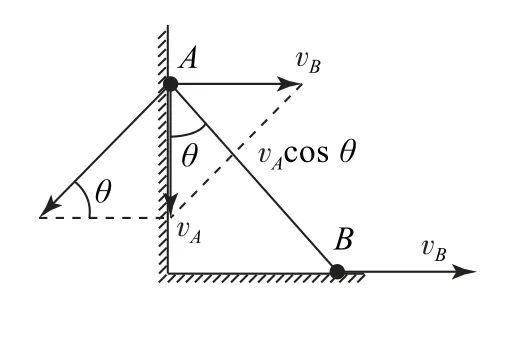
图9

点评

许多同学认为运动的合成与分解一定要正交分解,从这一例子可以看出,不一定要正交分解.同样的,斜抛运动也可以分解成沿初速度方向的匀速直线运动和竖直向下的自由落体运动.

例5一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点),将其放在一个光滑球形容器中从位置1开始下滑,如图10所示,当轻杆到达位置2时,球A与球形容器球心等高,其速度大小为v1,已知此时轻杆与水平方向成θ＝30°角,球B的速度大小为v2,则().

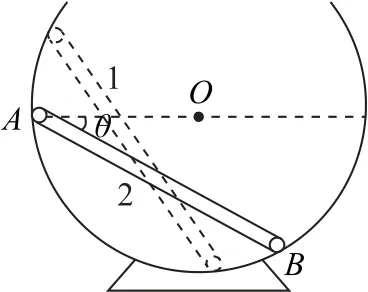
图10

解析

解法1效果分解法

小球A、B分别具有沿杆运动和垂直于杆转动的效果.将v1、v2分别沿杆和垂直于杆方向分解,由图知两球沿杆方向速度大小相等,即v1sinθ＝v2sinθ,得v1＝v2,故选项C正确.

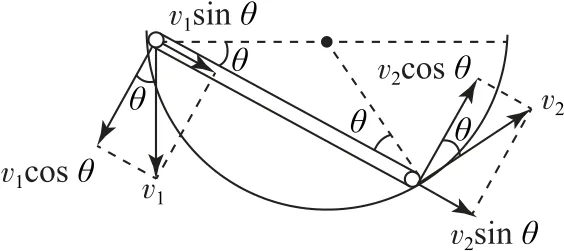
图11

解法2相对运动法

以球B为参考系,即假定B球静止,则A球绕B球做圆周运动.将A球的速度v1沿v2方向和垂直于杆方向分解如图12所示,其沿v2方向的分速度与v2相同,由矢量图可知v1＝v2.

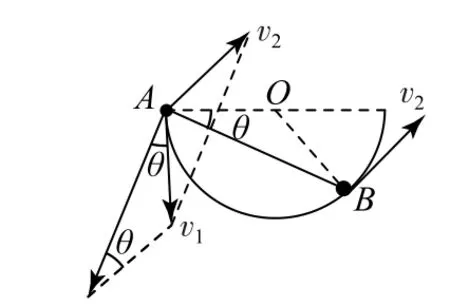
图12

解法3瞬时功率法

如图13所示,杆对两球的作用力大小分别为F1和F2,由牛顿第三定律知F1＝F2.两个力的瞬时功率的大小分别为P1＝|F1v1cos(90°＋θ)|,P2＝F2v2cos(90°－θ),由P1＝P2得v1＝v2.

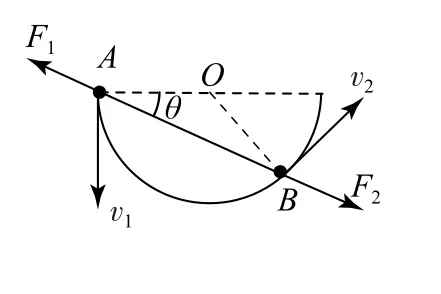
图13

例6如图14所示,一轻质细杆OA长为L,一端可绕固定在水平面上的轴转动,另一端固定一小球A.一高为h的木块B夹在水平面与细杆之间,此时杆OA与水平面成θ角,木块向右的速度为v,求此时A球的速度.

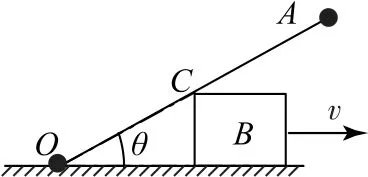
图14

解析

杆与木块的接触点是C点,C点的速度与木块B的速度相同,如图15所示,将木块B的速度沿杆和垂直于杆方向分解,得v1＝vsinθ,v2＝vcosθ,在任意时刻,细杆OA上各点绕O转动的角速度相同,可得,解得

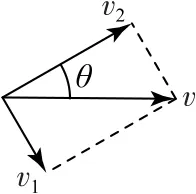
图15

点评

杆连接物体在沿杆方向速度相同,垂直于杆方向角速度相同.这就是效果分解法.

例7如图16 所示,细杆ABC靠在固定的半圆上,两者处于同一竖直平面内,杆的中点B恰好落在半圆上.已知A端沿半圆直径方向移动的速度大小为vA,试求C端的运动速度大小vC.

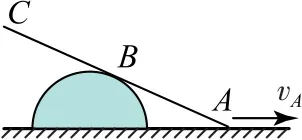
图16

解析

杆A端速度方向已知,此时杆中点B的法向速度为零,合速度方向沿杆方向,如图17 所示,分别作A、B速度垂线AD和BD交于D点,D点是A、C两点转动的瞬时圆心,即此时杆AC可认为在绕过D点且垂直于纸面的轴做定轴转动,杆上各点的速度方向均垂直于其到D点的连线.由速度公式有vC＝ω×rCD,vA＝ω×rDA,因为△CDB≌△ADB,所以rCD＝rAD,可得vC＝vA.

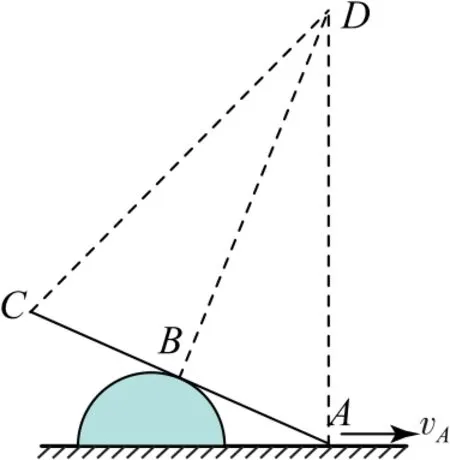
图17

点评

若某瞬时刚体上A、B两点的速度方向已知,且方向互不平行,可分别作两点速度矢量的垂线,使之交于一点,该点就是刚体转动的瞬时圆心,称为速度瞬心.

3 物物直接接触刚体模型

直接接触的两物体,由于两物体不发生形变,它们在垂直接触面方向的分速度和分加速度相等,若两物体在接触面无相对滑动,则它们沿接触面的切向分速度相同,反之,则不相同.

例8如图18所示,一个半径为R的半圆柱体沿水平方向以速度v0向右做直线运动,带动直杆沿竖直方向上升.杆与柱体的接触点为P,当P点和柱心O点的连线与竖直方向的夹角为θ时,求直杆的速度v.

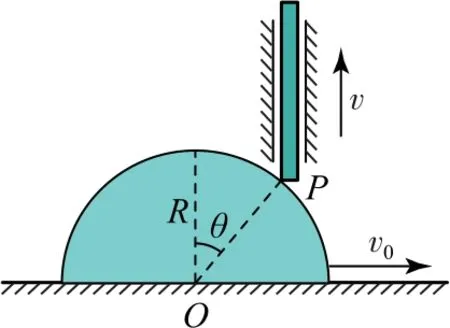
图18

解析

解法1效果分解法

杆上P点速度v沿OP方向的分量为vcosθ,柱体上P点的速度为v0,它沿OP方向的速度为v0sinθ,因杆与柱体始终接触,有vcosθ＝v0sinθ,得直杆的速度v＝v0tanθ.

点评

若两物体运动过程中是直接接触,则两物体在垂直接触面方向的分速度和分加速度相等,否则两物体将分离或形变.至于沿接触面的切向是否有相同的分速度,则取决于两物体在该方向上有无相对滑动,若沿接触面切向没有相对滑动,则接触双方将具有完全相同的分速度.

解法2相对运动法

以柱体为参考系,杆的速度沿切线向上,将杆的速度分解如图19所示.其水平分速度与柱体速度相同,另一分速度v1沿切线向上.由矢量图得,直杆的速度v＝v0tanθ.

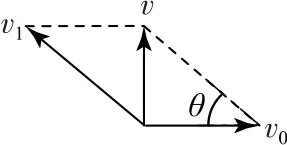
图19

解法3瞬时功率法

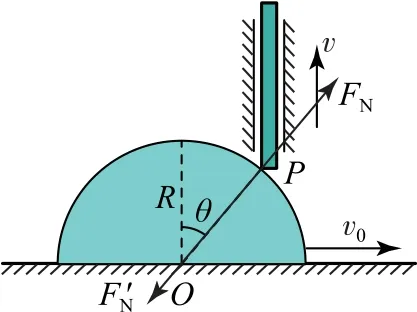
图20

设杆向上的速度为v,弹力FN对杆做功的瞬时功率大小为P1＝FNvcosθ,柱体克服弹力做功的瞬时功率大小为P2＝|0cos(90°＋θ)|,由P1＝P2得v＝v0tanθ.

4 小结

求解关联速度的方法一般有效果分解法、微元法、瞬时功率法,其中分解法主要基于绳或杆不可伸长,故沿绳或杆方向的分速度相同;微元法原理充分,但是相对复杂;瞬时功率法的根据是能量守恒定律,两连接体间的相互作用力的瞬时功率大小相等.当涉及杆转动问题时,要找到转动的瞬时圆心,杆上各点相对于圆心的角速度相同.直接接触的两物体沿接触面法向的分速度必定相同,沿接触面切向的分速度在无相对滑动时亦相同.

(完)