商业银行与第三方物流合作供应链金融的演化博弈研究

徐玲玲，丛雪薇

（哈尔滨商业大学 管理学院，黑龙江 哈尔滨 150028）

一、引言

党的十九届六中全会对习近平新时代中国特色社会主义思想做了系统概括，提出要“加快构建以国内大循环为主体、国内国际双循环相互促进的新发展格局”[1]，而发展供应链金融不仅仅是加快建设新发展格局的重要抓手，也是帮助受新冠肺炎疫情冲击的中小企业摆脱困境的重要方式[2]。供应链金融集金融管理、物流运作和商业运作于一体，将商业银行、第三方物流、融资企业等紧密地联系在一起，实现利用供应链运作盘活资金和用资金拉动供应链建设的目标[3]，同时解决中小企业因规模小、缺少健全的财务制度等长期面临的融资难题。在供应链金融运作中，中小企业多以存货质押作为融资方式，即中小企业将存货质押给商业银行，由商业银行指定的第三方物流对存货进行监督，商业银行依据第三方物流开具的存货证明为中小企业提供融资[4]。商业银行和第三方物流的密切合作能够帮助商业银行实现对融资企业的监管，显著降低融资风险，同时也给第三方物流带来了供应链金融增值业务，拓展客户群体和利润来源，整合供应链上下游物流业务，发挥规模经济效应，降低经营成本[5]，实现双方合作共赢。如商业银行与第三方物流合作，创新出优质的供应链金融产品，突破了以往供应链金融管理难度大的困难，实现了对货物的全程有效管控。

然而，在实际供应链金融业务中，由于信息不对称、中小企业和第三方物流的信用考核机制尚不完善，商业银行很难对质押标的物进行控制、对贸易真实性进行确认[6]，且商业银行与第三方物流往往是有限理性的，二者监督合约生效后，第三方物流可能会因为较大的投机收益选择与融资企业合谋，进行虚假交易或重复融资。如2013年虚假仓单质押骗贷案和2014年融资骗贷案等[7]，给商业银行造成了较大的经济损失，不利于双方形成良好的合作关系和供应链金融的稳定发展。二者只有良性合作才能降低第三方物流与融资企业的合谋风险[4]，从而形成健康的供应链金融网络生态系统[8]。因此如何在存货质押融资模式下建立并维持商业银行与第三方物流之间良好的合作关系，共同促进供应链金融发展，是亟待解决的关键问题。

目前，国内外学者们运用演化博弈方法对供应链主体间的合作问题展开了较多研究[9-12]，Li等（2018）[13]研究了全球供应链系统中供应商与制造商合作行为的演化博弈过程及影响因素。张琅等（2013）[14]构建了应收账款融资模式下商业银行与中小企业信贷行为的演化博弈模型，探究影响演化结果的因素。也有学者运用演化博弈方法揭示了供应链金融主体间的合作机理，李小莉和辛玉红（2017）[15]构建了银行与中小企业在供应链融资和传统融资模式下的信贷市场演化博弈模型。演化博弈方法克服了传统博弈的个体性以及纳什均衡的完全理性和完全信息的假设，参与主体根据其他参与方的策略采取行动，不断调整自身策略选择，实现动态平衡。随着电子商务的发展，学者们对电子商务与供应链金融结合的研究逐渐增多，徐鲲等（2017）[16]探究了电子商务背景下金融机构与供应链联盟的合作机制，探析演化均衡策略。杨青（2020）[17]研究了银行委托电商平台对融资企业进行授信管理时的银行监管问题。汪克峰和石岿然（2017）[18]构建了银行与电子商务平台的委托代理演化博弈模型，研究了二者的策略选择问题。近年来区块链技术兴起，学者将区块链技术引入供应链金融，黄海涛等（2021）[19]构建政府采购部门、中小企业和银行的三方博弈模型，对各主体的决策进行分析，并构建区块链技术下的演化博弈模型来分析链上主体的策略选择。周雷等（2021）[20]构建金融机构与小微企业、核心企业与小微企业的演化博弈模型，得出区块链能够促使核心企业与小微企业向“双守信”的理想状态演化的结论。由此可见，国内外学者运用演化博弈方法从主体合作、电子商务平台以及区块链技术等方面对供应链金融主体的演化策略进行了研究，多以商业银行与中小企业、商业银行与电子商务平台的策略选择作为研究重点，仅有少数学者运用演化博弈方法对商业银行与第三方物流的合作问题进行了研究，马娟和万解秋（2015）[21]从竞合角度研究金融机构与物流企业的合作机制，但没有考虑对退出协作方进行惩罚这一因素。柴正猛和段黎黎（2018）[4]对银行与物流企业仓单质押融资业务中的银行监督行为和物流企业包庇行为进行了分析，探究了影响演化稳定策略的因素。

鉴于此，本文拟在借鉴前人研究结果的基础上，运用演化博弈方法构建商业银行与第三方物流合作供应链金融的演化博弈模型，探究二者的演化稳定策略，明晰影响系统演化结果的关键因素，并提出加强供应链金融数字化生态化建设、提高第三方物流信用水平等建议，以确保二者良好合作，从而促进供应链金融的发展。本研究以促成商业银行与第三方物流良好的合作关系为目的，不同于以往学者探讨的商业银行与第三方物流之间的竞合行为、监督包庇行为，具有一定的创新性和理论贡献，并对商业银行与第三方物流合作供应链金融提出了具体的、有针对性的建议。

二、演化博弈模型构建与分析

（一）模型假设

假设商业银行B和第三方物流L是供应链金融系统中的两大主体。

假设B与L进行博弈策略选择时，双方的博弈策略均为合作或不合作。当商业银行采取合作策略时，商业银行会与第三方物流合作发展供应链金融业务，需要付出合作成本，同时也会获得额外的合作收益；商业银行也会因较大投机收益而选择退出协作，自行投入物流资源、开展相关物流活动，与第三方物流形成竞争关系，会给第三方物流带来一定的损失。当第三方物流采取合作策略时，第三方物流会加大业务开拓、资源投入的力度，与商业银行共同发展供应链金融业务，也需付出合作成本和获得合作收益；同时第三方物流也会因较大的投机收益而选择退出协作，不与商业银行合作供应链金融业务，如不再对其授信下的货物进行监督，不再向商业银行发出预警信号；或者自行开展供应链金融业务，甚至联合融资企业欺骗商业银行的信贷，给商业银行造成损失。

另外，本文还假设B与L组成的供应链金融合作系统是遵循自然选择法则演化的，没有政府等相关机构的干预。

（二）变量设定与博弈分析

1.变量设定

博弈的双方包括商业银行B和第三方物流L，双方的博弈策略分别为（合作，不合作）和（合作，不合作），选择合作策略的概率分别为x、y(0≤x≤1，0≤y≤1)，选择不合作策略的概率分别为(1-x)、(1-y)，且均是时间的函数，即x=x(t)、y=y(t)。

在不合作状态下，B与L单独进行供应链金融业务或物流服务时所获得的收益分别为WB、WL；B和L付出的合作成本分别为CB、CL，主要包括寻求成本和监督成本等；ΔW为B和L合作时所获得的额外收益，B为L提供了增信服务，拓宽业务群，吸收更多客户，L为B授信下货物的流通进行监督以及带来新的客户群体等，二者信息共享、优势互补，带来额外的收益，α为额外收益的分配系数；当B选择合作策略时，L方会因投机收益Δr而选择退出合作（此时的投机收益包括了为合作而付出的初始成本），而被迫退出合作的B方会遭受损失TB，包括信誉损失和利润损失（其中不包含初始合作成本），反之当L选择合作策略时，B会因投机收益Δs而选择退出合作，L将遭受损失TL；同时退出合作的一方将会受到惩罚P。

2.博弈分析

结合以上变量的设定情况，得到商业银行B与第三方物流L的收益矩阵如表1所示。

表1 B与L的博弈收益矩阵

根据表1的博弈收益矩阵，分别计算供应链金融中B与L采取合作策略的复制动态方程。

（1）计算B选择合作策略时的复制动态方程。

根据Malthusian方程[22]，B选择合作策略的复制动态方程为：

根据博弈收益矩阵可知B选择合作策略和不合作策略的期望收益分别为：

B的平均期望收益为：

由式（1）—式（4）可得B选择合作策略的复制动态微分方程为：

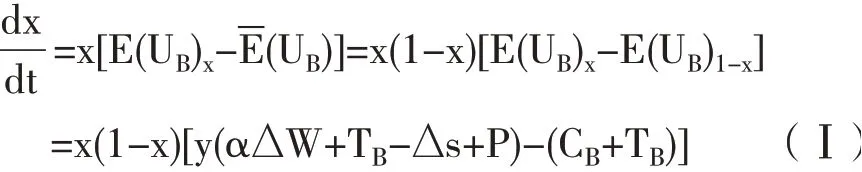
（2）计算L选择合作策略时的复制动态方程。

同理L选择合作策略的复制动态方程为：

L选择合作策略和不合作策略的期望收益分别为：

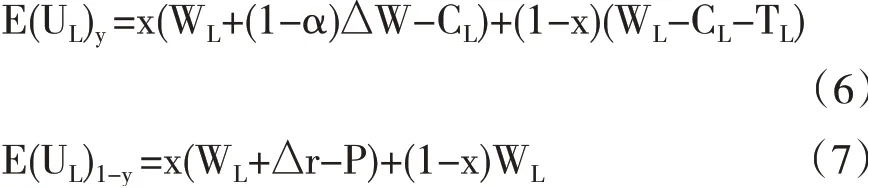
L的平均期望收益为：

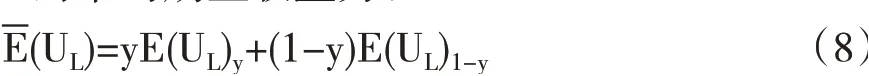
由式（5）—式（8）可得L选择合作策略的复制动态方程为：

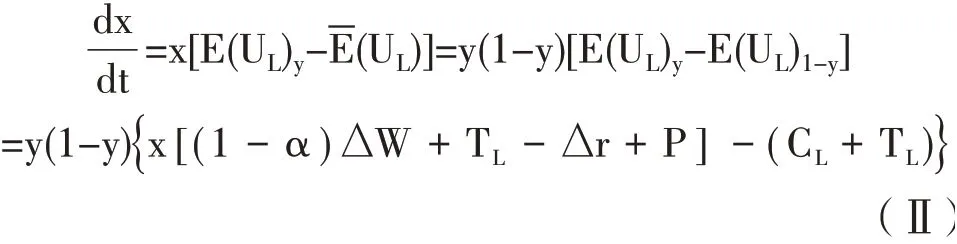
复制动态方程（Ⅰ）与（Ⅱ）描述了商业银行B与第三方物流L在供应链金融业务中选择合作策略或不合作策略的演化动态。依据以上两个方程，即可对B和L的供应链金融合作系统进行均衡分析和均衡点的稳定性分析。

三、演化博弈均衡分析

演化稳定策略（ESS）是群体经过反复博弈后选择的某个最优的稳定策略。演化稳定策略的确定要根据商业银行B和第三方物流L这两个群体的复制动态方程，得到纳什均衡点；再计算出雅可比矩阵的值detJ和迹trJ，进行均衡点的稳定性分析，得到演化稳定策略。

（一）求解复制动态方程（Ⅰ）与（Ⅱ）

令复制动态方程（Ⅰ）与（Ⅱ）等于0，得到商业银行B与第三方物流L行为策略的五个纳什均衡点

（二）式（Ⅰ）与（Ⅱ）分别对x、y求偏导

令（Ⅰ）与（Ⅱ）分别对x、y求偏导可得到雅可比矩阵J：

（三）计算雅可比矩阵J的值det J和迹tr J

（四）分别计算各纳什均衡点的det J和tr J

根据Friedman的判别方法[23]，如果均衡点ei(xi,yi)（其中i=1,2,…,5且0≤xi，yi≤1）的detJ＞0且trJ＜0，则该均衡点具有稳定性。在合作过程中，可能会出现一方退出协作的情况，是因为投机净收益（即投机收益-惩罚）大于额外净收益（即额外收益-成本），不合作的一方受投机净收益驱使选择退出协作，所以对以下四种情况下B与L合作系统的均衡点进行稳定性分析，如表2所示。

表2 均衡点分析条件

（1）当αΔW-CB＞Δs-P，(1-α)ΔW-CL＞Δr-P时，均衡点ei(xi,yi)，i=1,2,…,5，均满足0≤xi，yi≤1，所以e1～e5均为B与L合作系统的均衡点。条件（1）下均衡点稳定性分析如表3所示。

表3 条件（1）下B与L合作系统的均衡点稳定性分析

根据表3可知，B与L合作供应链金融业务时，若双方的额外净收益均大于投机净收益，则B和L合作系统存在e1(0,0)和e4(1,1)两个ESS。这意味着当系统达到稳定状态时，两个博弈主体存在（不合作，不合作）或（合作，合作）两种稳定策略。此时B和L的博弈动态演化图如图1所示。

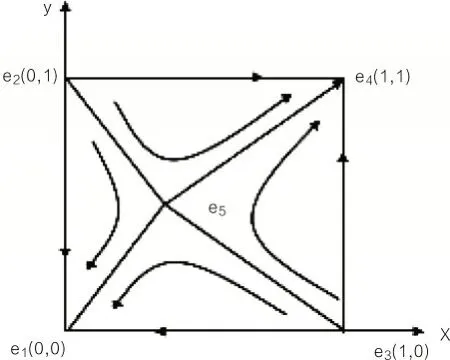
图1 条件（1）下的动态演化路径图

（2）当αΔW-CB≤Δs-P，(1-α)ΔW-CL≤Δr-P时，均衡点ei(xi,yi)，i=1,2,…,4，满足0≤xi，yi≤1，所以e1～e4均为商业银行B与第三方物流L的供应链金融合作系统的均衡点。

当αΔW-CB＜Δs-P时当(1-α)ΔW-CL＜Δr-P时不满足均衡点ei(xi,yi)中0≤xi，yi≤1的条件；当αΔWCB=Δs-P，(1-α)ΔW-CL=Δr-P时，均衡点e5与e4(1,1)重合，不再是均衡点。条件（2）下均衡点稳定性分析如表4所示。

根据表4可知，B与L合作供应链金融时，如果双方的额外净收益均小于投机净收益时，B和L均会选择不合作策略，e4(1,1)不具有稳定性。B和L合作系统存在唯一的ESS：e1(0,0)，意味着两个博弈主体存在（不合作，不合作）这一唯一的稳定策略。此时B和L的动态演化图如图2所示。

图2 条件（2）下的动态演化路径图

表4 条件（2）下B与L合作系统的均衡点稳定性分析

（3）当αΔW-CB＞Δs-P，(1-α)ΔW-CL＜Δr-P时，均衡点ei(xi,yi)，i=1,2,…,4，满足0≤xi，yi≤1，所以e1～e4均为商业银行B与第三方物流L的供应链金融合作系统的均衡点。

当(1-α)ΔW-CL＜Δr-P时不满足均衡点ei(xi,yi)中0≤xi≤1的条件，所以e5不再是均衡点。条件（3）下均衡点稳定性分析如表5所示。

表5 条件（3）下B与L合作系统的均衡点稳定性分析

根据表5可知，B与L合作供应链金融时，如果B获得的额外净收益大于投机净收益，而L获得的额外净收益小于投机净收益，此时L会选择不合作策略，e2(0,1)不具有稳定性。B和L合作系统存在e1(0,0)这一唯一的ESS，意味着博弈主体存在唯一的（不合作，不合作）稳定策略。此时B和L的动态演化图如图3所示。

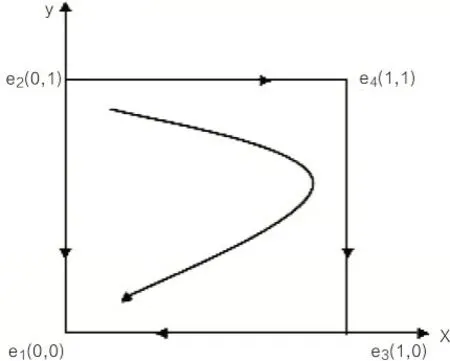
图3 条件（3）下的动态演化路径图

（4）当αΔW-CB＜Δs-P，(1-α)ΔW-CL＞Δr-P时，均衡点ei(xi,yi)，i=1,2,…,4，满足0≤xi，yi≤1，所以e1～e4均为商业银行B与第三方物流L的供应链金融合作系统的均衡点。

当αΔW-CB＜Δs-P时不满足均衡点ei(xi,yi)中0≤xi≤1的条件，所以e5不是均衡点。条件（4）下均衡点稳定性分析如表6所示。

表6 条件（4）下B与L合作系统的均衡点稳定性分析

根据表6可知，B与L合作供应链金融时，如果B获得的额外净收益小于投机净收益，而L获得的额外净收益大于投机净收益，此时B会选择不合作策略，e3(1,0)不具有稳定性。B和L合作系统存在e1(0,0)这一唯一的ESS，意味着博弈主体存在唯一的（不合作，不合作）稳定策略。此时B和L的动态演化图如图4所示。

图4 条件（4）下的动态演化路径图

综上所述，仅当商业银行和第三方物流的额外净收益（即额外收益-成本）均大于投机净收益（即投机收益-惩罚）时，存在两个ESS，为e1(0,0)和e4(1,1)。在其他三种情况下，任何一方的额外净收益小于净投机收益时，存在e1(0,0)这一唯一的ESS。即只有当B和L两参与方的额外净收益均大于投机净收益且额外收益得到合理分配的情况下，博弈主体才可能选择（合作，合作）的策略，否则合作系统将在长期演化过程中趋向于（不合作，不合作）。

四、商业银行与第三方物流合作策略的影响因素分析

由上述博弈均衡分析可知，当B和L的额外净收益均大于投机净收益时，B与L的稳定策略选择为（不合作，不合作）和（合作，合作），其他情况下的稳定策略为（不合作，不合作）。所以额外净收益、投机净收益是演化稳定策略的关键影响因素。B和L合作系统的演化结果趋向于e1(0,0)还是e4(1,1)，主要取决于博弈初始状态和鞍点e5的位置，这由e1e2e5e3的面积S1和e4e3e5e2的面积S2大小来决定。当S1＞S2时，S1面积更大，鞍点e5更接近于e4(1,1)，则B与L合作系统的初始状态落在e1e2e5e3的概率更大，意味着多次演化博弈的结果趋向于e1(0,0)，双方更倾向于选择（不合作，不合作）策略；当S1＜S2时，S2面积更大，鞍点e5更接近于e1(0,0)，则B与L合作系统的初始状态落在e4e3e5e2的概率更大，演化博弈的结果趋向于e4(1,1)，双方更倾向于选择（合作，合作）策略；当S1=S2时，面积相等，意味着双方选择合作与不合作策略的概率相等。

由图1可知，面积的计算公式为：

由式（Ⅲ）可知影响S1的因素有6个：额外收益、投机收益、损失、成本、惩罚、收益分配系数。进一步分析可得出以下结论。

结论1：商业银行与第三方物流合作供应链金融时获得的额外收益越大，双方选择合作策略的概率将增大。

证：

所以S1是ΔW的单调减函数，双方合作供应链金融业务时获得的额外收益越大，S1的面积将越小，系统向e4(1,1)方向演化的概率将增大，商业银行与第三方物流选择合作策略的概率将增大。

结论2：当一方选择合作策略而另一方选择不合作策略时，不合作的一方获得的投机收益越大，双方合作供应链金融业务的概率越小。

证：

所以S1是Δs的单调增函数，当第三方物流选择合作供应链金融，而商业银行不合作时，随着商业银行退出协作获得的投机收益越大，S1的面积将越大，系统向e1(0,0)方向演化的概率将增大，双方合作进行供应链金融的意愿就会减小。同理，当第三方物流退出协作获得的投机收益增加时，双方合作进行供应链金融的动机也会减小。

结论3：当一方选择合作策略而另一方选择不合作策略时，选择合作策略的一方受到的损失越大，双方合作进行供应链金融业务的概率越小。

所以S1是TB的单调增函数，根据演化博弈均衡分析可知，只有当αΔW-CB＞Δs-P，(1-α)ΔW-CL＞Δr-P时，双方才有可能选择（合作，合作）策略。当商业银行选择合作供应链金融，而第三方物流不合作时，随着第三方物流退出协作给商业银行带来的损失越大，S1的面积将越大，系统向e1(0,0)方向演化的概率将增大，双方合作进行供应链金融的意愿就会减小。同理，当商业银行退出协作给第三方物流带来的损失越大，双方合作进行供应链金融的动机就会越小。

结论4：商业银行与第三方物流合作供应链金融的概率随着寻求成本、监督成本等的增加而减小。

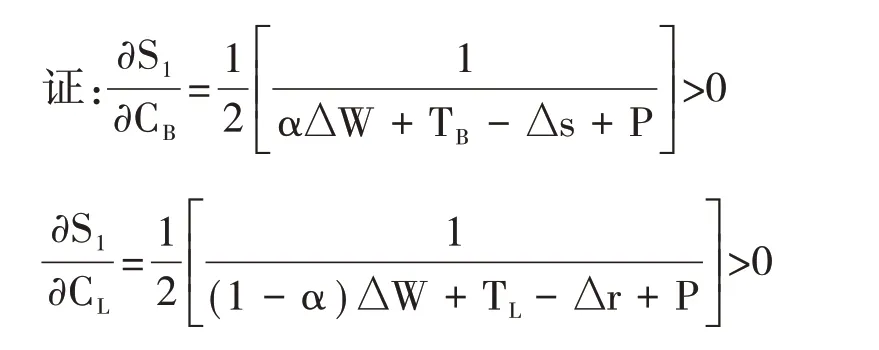
所以，S1是CB的单调增函数，当商业银行初始合作成本越大时，S1的面积将越大，系统向e1(0,0)方向演化的概率将增大，商业银行选择合作策略的概率将减小。同理，当第三方物流投入的成本增加时，第三方物流选择合作进行供应链金融的意愿也将减小。

结论5：当一方选择合作策略而另一方选择不合作策略时，不合作的一方受到的惩罚越大，双方合作进行供应链金融业务的概率越大。

证：

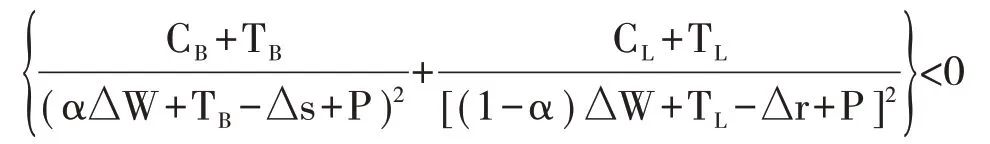
所以S1是P的单调减函数，当第三方物流选择合作供应链金融，而商业银行不合作时，随着商业银行退出协作受到的惩罚越大，S1的面积将越小，系统向e4(1,1)方向演化的概率将增大，双方合作进行供应链金融的概率就会增大。同理，当第三方物流退出协作受到的惩罚增加时，双方合作进行供应链金融的意愿就会增加。

结论6：当其他因素一定时，存在一个最优的额外收益分配比例，使得双方均选择合作策略的概率最大化。

证：

α对S1的影响是非单调的，所以S1要对α求二阶导数，得到：

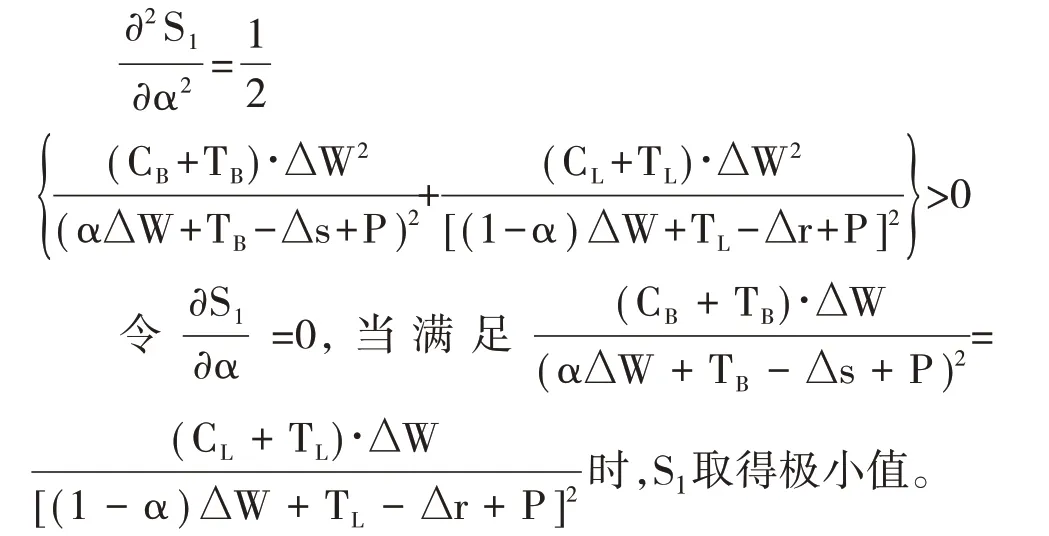
此时系统向e4(1,1)方向演化的概率最大，商业银行与第三方物流合作进行供应链金融的可能性最大，此时α为额外收益分配结果的最优解。

五、研究结论与建议

本文以构建商业银行与第三方物流良好的合作关系为目的，运用演化博弈方法对有限理性与不完全信息的商业银行与第三方物流的合作博弈行为进行分析，探究影响系统演化博弈均衡的因素，并提出促进商业银行与第三方物流形成良好合作关系的相关建议。研究表明：（1）只有当商业银行与第三方物流的额外净收益均大于投机净收益时，双方才有合作的可能性，任意一方的额外净收益小于投机净收益时，双方均向（不合作，不合作）的博弈均衡点靠拢，难以形成良好的合作关系以共同发展供应链金融业务。（2）额外收益、投机收益、损失、初始合作成本、惩罚等是影响商业银行与第三方物流形成良好合作关系这一演化结果的关键因素，同时还须制定合理的额外收益分配系数，保障额外收益在二者之间的合理分配。（3）商业银行与第三方物流合作获得的额外收益越大、所需初始合作成本越小，双方越倾向于选择合作策略；商业银行或第三方物流获得的投机收益越大、对方退出协作给自身造成的损失越大、退出合作一方受到的惩罚越小，双方越难达成合作关系。

据此，要想促成商业银行与第三方物流达成良好的合作关系，共同进行供应链金融服务，应该紧扣上述影响因素，有针对性地采取措施。

（1）加强供应链金融数字化生态化建设。

一是商业银行应着力打造“区块链+供应链金融”平台，创新数字化供应链金融产品。习近平总书记强调要“推动区块链和实体经济深度融合，解决中小企业贷款融资难、银行风控难、部门监管难等问题”。应充分利用区块链等数字技术实现对供应链金融业务总量、融资商品、监管企业合作情况等的分布式存储、统计，实现融资货物质押与解押操作、报表统计、风险提示信息、风险情况分析等工作的数字化，使业务操作流程化、透明化。二是商业银行需要建立“金融+区块链”的人才队伍。当前在数字经济时代，我国对金融人才、数字人才的需求逐年上升，应培养了解区块链技术原理、熟悉供应链金融业务模式和特点、掌握风控思维及风控方法的专业人才，同时设立相应的考核机制，保证从事供应链金融业务的人员水平，防止出现不合规的行为。三是商业银行应加强与第三方物流的资源共享与合作，与第三方物流的管理系统（如WMS仓库管理系统）实现信息互联互通，利用区块链技术整合物流、资金流、信息流，及时核验存货、仓单、订单的真实性和有效性，并建立数字化风控系统，实现实时监控，构建数字供应链金融新生态。

（2）守信激励与失信惩罚相结合。

在存货质押融资业务中，第三方物流企业发挥了重要作用，其业务能力与努力水平是决定存货质押业务能否有效运作和健康发展的关键因素。一是商业银行应给予第三方物流与其努力程度相匹配的激励报酬，对实施有效监督的第三方物流适当增加报酬比例，使第三方物流有足够的超过灰色报酬的净收益，促使第三方物流采取合规行为，促进双方良性合作关系的建立；二是商业银行应设置相应的违规惩罚机制，加大对第三方物流不合规行为的惩处力度，使其在较高的惩罚成本下减少投机行为，约束和规范第三方物流与融资企业的合谋骗贷行为；三是商业银行应及时跟踪存货质押货物的状态，实时监控第三方物流的动态，一旦发现违约行为立即采取惩处或终止融资业务合同、收回货款等措施，以减少自身损失。

（3）商业银行应完善资信核查制度。

从实质上看供应链金融是一种信用担保，当前，商业银行在开展供应链金融业务时最常涉及的是信用风险。目前我国尚未建立起完整的供应链企业资信核查制度及信用评价制度。一是商业银行应完善资信核查制度，建立第三方物流、融资企业的审核准入机制，建立专门的调查、审查部门，调查融资企业、第三方物流的运营情况、资信状况、偿债记录等以及审查贸易背景的真实性；二是商业银行应对融资业务的风险进行评级，根据不同的风险等级调整融资企业的授信期限，并建立针对融资企业、第三方物流的保证金机制；三是采用“评价模型+专家打分”方式对第三方物流的规模、职工队伍素质、管理水平、信用记录等进行严格评估，选择经营规模大、资信情况好、管理技术先进、监管程序严谨、员工素质高的优质第三方物流进行供应链金融业务的质押监管，加大对第三方物流的不定期检查制度。

（4）第三方物流应做好质押物监管，并提升自身信用。

一是存货质押融资业务多涉及产权转移、价格波动等问题，第三方物流应协助商业银行选择在产权、价格波动、变现能力等方面优质的质押物，在质押贷款期间，第三方物流应对仓单、质押货物进行有效监管，对质押物价格变动等异常情况进行有效观测和控制，预防出现重复质押或虚假仓单等骗贷行为；在融资企业违约时，第三方物流要协助商业银行做好善后的处理工作，提供有力的证据。二是在第三方物流完全竞争市场中，声誉对第三方物流具有较强的约束力，第三方物流应重视自身声誉的资产化，注重自身形象和信誉的树立，强化自身能力、责任和担当，不断提升自身核心竞争力，努力赢得商业银行的信任，从而赢得更多与商业银行合作供应链金融业务的机会。三是第三方物流应与商业银行保持长期的良好合作关系，由于商业银行与第三方物流的合作是多次的，只要第三方物流的短期利益小于长期利益，理性的第三方物流就会选择合作，减少机会主义行为。第三方物流应在信息不对称的情况下为商业银行提供融资企业和质押货物、仓单的可靠信息，拒绝发生因投机收益等利益引诱而与贷款企业合谋骗取商业银行融资的“背德”行为，努力促进自身业务的拓展和实现供应链金融良性发展。

（5）政府应加强对供应链金融业务的监管与支持。

目前我国对商业银行、第三方物流、融资企业的监管机制、金融制度尚不完善，缺少统一的融资担保登记制度。一是政府和相关监管部门应制定详细的监管机制，制定《供应链金融监督管理条例》等统一的监管标准，加大对商业银行、第三方物流、融资企业的监管力度，并出台《失信惩戒条例》等处罚性文件，进一步完善《担保存货第三方管理规范》《中华人民共和国物权法》《动产抵押登记办法》《中华人民共和国担保法》等细则，提供良好的法律环境；二是建立统一的登记制度和公共信息平台，避免多次登记、重复担保问题，政府应设立相应的金融风险监测与防控中心，构建更高层次的风控体系和制定完善的金融制度，为供应链金融发展营造健康良好的发展环境。