适用于网格状的交直流微网协调控制策略
2022-04-21牛茜张东王军龙
牛茜,张东,王军龙
(1.山西机电职业技术学院电气工程系,山西 长治 046000;2.太原理工大学电力系统运行与控制山西省重点实验室,山西 太原 030024;3.国网山西省电力公司计量中心,山西 太原 030024)
近年来,交直流混合微网由于具有两种微网的优点而受到广泛关注[1]。交直流混合微网的主要控制目标为功率分配[2]、电压/频率调节[3]和维持系统稳定[4]。在这些目标中,分布式电源之间的功率分配是关键问题之一。目前,下垂控制已广泛应用于微网功率分配控制[5-8]。例如,在文献[7]中,为实现交流和直流子网之间的比例功率共享,提出了一种双向下垂控制方案来控制互连转换器(interlink converters,ICs)。多个微网间的功率互济可有效提升电网运行的可靠性和灵活性。近年来,针对这一问题,国内外专家开展了一定研究,如文献[3]、文献[9-11]。但这些研究仅考虑了直流微网[9]或交流微网[11]集群,而未考虑通过双向DC-AC互连转换器连接的混合交直流微网[10]。因此,本文针对采用DC-AC和DC-DC互连转换器的多端直流系统(multi-terminal direct current,MTDC)连接的交流/直流微网间的功率分配问题进行研究。
由于功率变流器的高穿透性大大降低了微网的惯性,给系统稳定性带来了很大威胁。惯量[12]和调速器响应速度[13]是决定系统稳定性的两个关键因素。目前,虚拟同步发电机(virtual synchronous generator,VSG)技术[14]等惯量仿真技术对解决这一问题有着十分广阔的前景。已有的研究可以分为两类,即固定惯量和自适应惯量。第一类方法主要集中在虚拟同步发电机本身和微网的应用上[14-16]。例如,文献[15]提出了一种基于双向并网变换器的直流永磁同步电动机虚拟惯量控制策略,为直流母线电压提供惯量。然而,当微网离网时,这种方法便无法提供惯量。对于混合交/直流系统,已有文献开展了相关研究。文献[17-18]提出了基于VSGs和微分控制的控制策略,以提高负载变化时系统稳定性。文献[19]通过MTDC电网和海上风电场开发了基于比例的选择惯性和主频率支持。然而,这些工作主要集中在无法根据系统干扰进行自适应调整的固定惯性上,因此,无法获得良好的控制效果。
基于此,本文将重点放在网格状交直流微网的体系结构和控制方案上,从而实现可再生能源的优化利用,提高系统的稳定性,同时保持适当的功率分配。
1 网格状交直流微网的自适应控制策略
图1为基于低压多端直流系统的网格状交直流微网结构图。
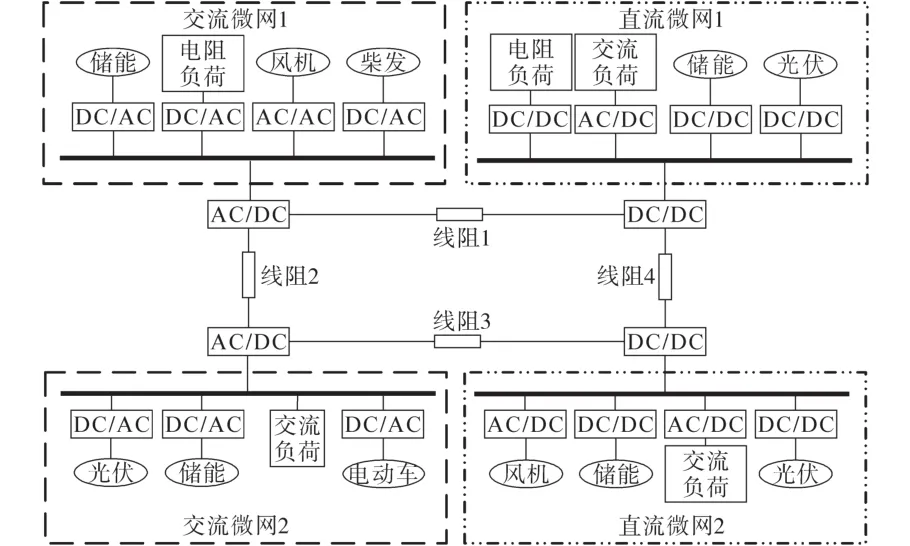
图1 基于低压多端直流系统的网格状交直流微网结构图Fig.1 Structure diagram of grid AC-DC microgrid based on low-voltage multi-terminal DC system
由图1可知,上述交直流微网系统含有两个交流微网和两个直流微网,且每个微网都有自己的电源、存储和负荷。相邻位置的交流或直流微网通过多端直流变流器相互连接,网格状交直流微网系统既可以与大电网并网运行,也可以独立运行。本文主要讨论网格状交直流微网系统的独立运行模式。
1.1 基于自适应虚拟惯量和虚拟调速器增益的连接变流器的控制器
图2为交直流微网连接变流器的控制方框图。
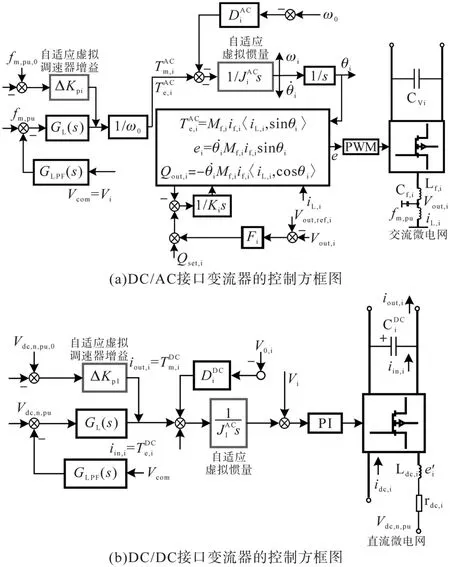
图2 网格状交直流微网连接变流器的控制方框图Fig.2 Control block diagram of grid-like AC/DC microgrid connected converter
由图2可知,除了功率分配控制器,本文所提控制方法还包括2个部分:自适应虚拟惯量调节策略和自适应虚拟调速器增益调节策略。直/交流连接变流器的控制器数学表达式为
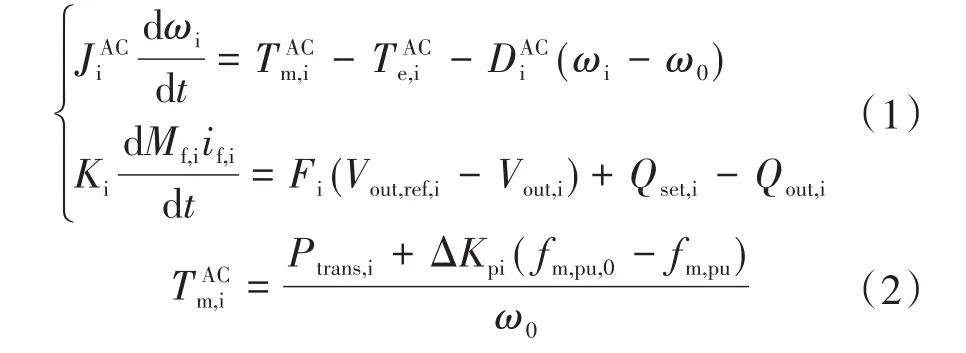

1.2 自适应虚拟惯量和虚拟调速器增益的设计
1.2.1 自适应虚拟惯量的设计
众所周知,频率变化率和直流电压变化率既反映了大量负载或大量电源变化所引起的扰动规模,也反映了系统的惯性水平。较大的扰动会导致较高的频率变化率和直流电压变化率,这意味着频率或直流电压在开始阶段下降迅速。因此,为了抑制系统在受到扰动后频率变化率和直流电压变化率迅速下降,提升系统的惯性将提升系统的稳定性,此外,较好的系统惯性可以保障系统在受到扰动后相关参数能快速恢复到正常范围内。根据以上分析,Ji可以给出为

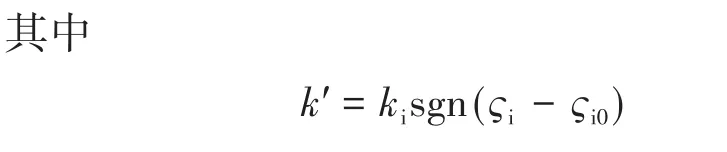
式中:ki为交/直流接口变流器kac,i或直/直流接口变流器kdc,i;kac,i,kdc,i均为可调节常数;Ji0为Ji的稳态值;Ji,max,Ji,min分别为Ji的最大值和最小值。
由式(5)可知,当系统受扰时,频率变化率或直流电压变化率为最大值。k′dςi/dt位于水平轴的最右端,惯性系数较大,证明满足上述分析。当频率变化率或直流电压变化率减小时,惯性系数也慢慢减小到Ji0,直到频率变化率或直流电压变化率等于零。当k′dςi/dt<0时,惯性系数继续减小,这就保证了系统在反弹期间具有良好的动态响应。
1.2.2 自适应虚拟调速器增益的设计
为了进一步提高系统的稳定性,本文设计一种方法来自适应地调整这些在多端直流系统中变换器的虚拟调速器的响应速度。每个变流器在受到扰动时都可以运行在两种不同的模式下,即发电机模式(generator mode,GM)或电机模式(motor mode,MM)。例如,当一个互联的交直流微网中的负载发生突变时,如果与之相连的变流器向受干扰的微网注入电能,它就工作在GM模式,反之亦然。因此,对于GM模式,虚拟调速器增益的设计应基于系统频率、直流电压和虚拟转子转速。较大的系统频率、直流电压要求虚拟调速器满足快速的响应速度,而高的虚拟转子转速可以为虚拟发电机提供大的动能供其吸收,从而快速支撑一次频率和直流电压。对于MM模式,虚拟调速器增益的设计应以虚拟转子转速和频率及直流电压为基础。大的虚拟转子速度反映大的虚拟动能,因此,工作在MM模式的变流器并不能提供更多的电能。另一方面,高频率或高直流电压反映出更多的电能可以由未受扰动的微网提供。因此,当虚拟转子转速、系统频率和直流电压相对较大时,GM模式的虚拟调速器增益应设计得较大,反之亦然。当虚拟转子转速较小,系统频率或直流电压较大时,在MM模式的虚拟调速器增益应较大,反之亦然。因此,根据上述思路,将虚拟调速器增益两个部分,具体设计如下:
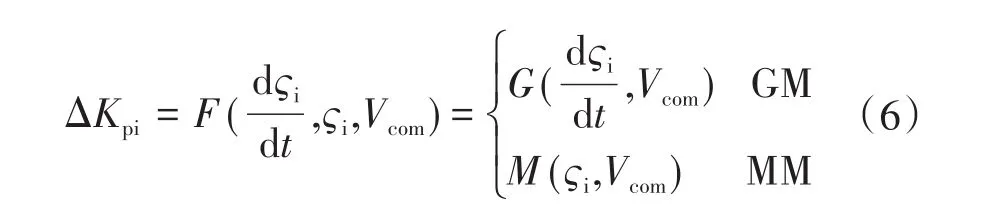

2 系统稳定性分析与参数选择
2.1 网格状交直流微网的小信号模型


2.2 小信号稳定性分析及参数选择
本节着重讨论虚拟惯性和虚拟调速器增益扰动对系统稳定性的影响。根据式(16)所示的模型,具有虚拟惯性系数JAC和JDC的特征值轨迹分别由1e-2变化到15和1e-2变化到30。虚拟调速器增益系数均由1e3变化到5e3。图3为控制参数变化的根轨迹。

图3 控制参数变化的根轨迹Fig.3 The root locus with control parameters varying
由图3a可以看出,当虚拟惯量JAC很小时,系统特征值非常接近于右平面,当系统受到扰动时,稳定状态很容易被破坏。随着JAC的逐渐增大,系统特征值向左平面移动,并逐渐远离虚轴,这就在一定程度上增强了系统的阻尼。随着JAC的不断增大,特征值实部趋于零,当其大于14.9时,这将导致系统不稳定。对于根轨迹,通过改变虚拟惯量JDC,可以得到与改变JAC相同的效果。由图3b可得,随着JDC的增大,系统特征值逐渐远离虚轴,并向左平面移动,这就增强了系统的阻尼,提高了系统的稳定性。但随着JDC的进一步增大,系统特征值开始靠近虚轴,并向右平面移动,不利于系统的稳定性。由此可知,较小的虚拟惯量可以提高系统的响应速度,但以损失稳定裕度为代价;另一方面,系统的相位裕度与虚惯量成反比关系。由图3c可以看出,系统特征值随着的逐渐增大而远离虚轴,这就增强了系统的阻尼。但随着的进一步增大,系统特征值开始向右半平面移动,大于4 890时,就会破坏系统的稳定性。改变有类似的效果。由图3d可得,随着的逐渐增大,系统特征值向左平面移动,并远离虚轴,这就提高了系统的稳定性。但随着的进一步增大,系统特征值开始向右半平面移动,大于4 760时,就会破坏系统的稳定性。
3 仿真分析
为验证本文所提方法的可行性与有效性,本文仿真系统结构图见图1。系统相关参数如下:AC MG:f=50 Hz,Pac,load=11 kW/23 kW;DC MG:Vdc,0=400 V,Pdc,load=5 kW;直/交流接口变流器:Vcom,ref=700 V,Vout,ref=311 V,K=7.1,L=6 mH,Lf=3 mH,Cf=500 μF,F=321,CV1=2 mF,DAC=22;虚拟惯量:J0=2,Jmax=8,Jmin=0.5;线路阻抗:
系统频率和直流电压的允许范围分别为49.5~50.5 Hz和390~410 V。将连接到两个子系统的负载在轻、重两种工况下进行切换,以验证本文控制策略的有效性。首先,交直流微网在“轻负载”状态下稳定运行。在t=4 s时,交流端负载由轻变重。在t=9 s时,当微网达到稳态时,在交流侧的负载恢复到初始配置。
本文着重提高交流侧和直流侧负载变化时频率和直流电压的动态稳定性。针对上述仿真系统采用4种不同控制策略进行了比较和验证。方法一:传统下垂控制,虚拟惯量J0设置为0.5;方法二:虚拟惯量被设为一个较大常数(J0=8);方法三:本文所提方法(仅含自适应虚拟惯量);方法四:本文所提方法。图4为不同控制方法下惯性和调速器增益在负载变化时对交流侧和直流侧的影响。
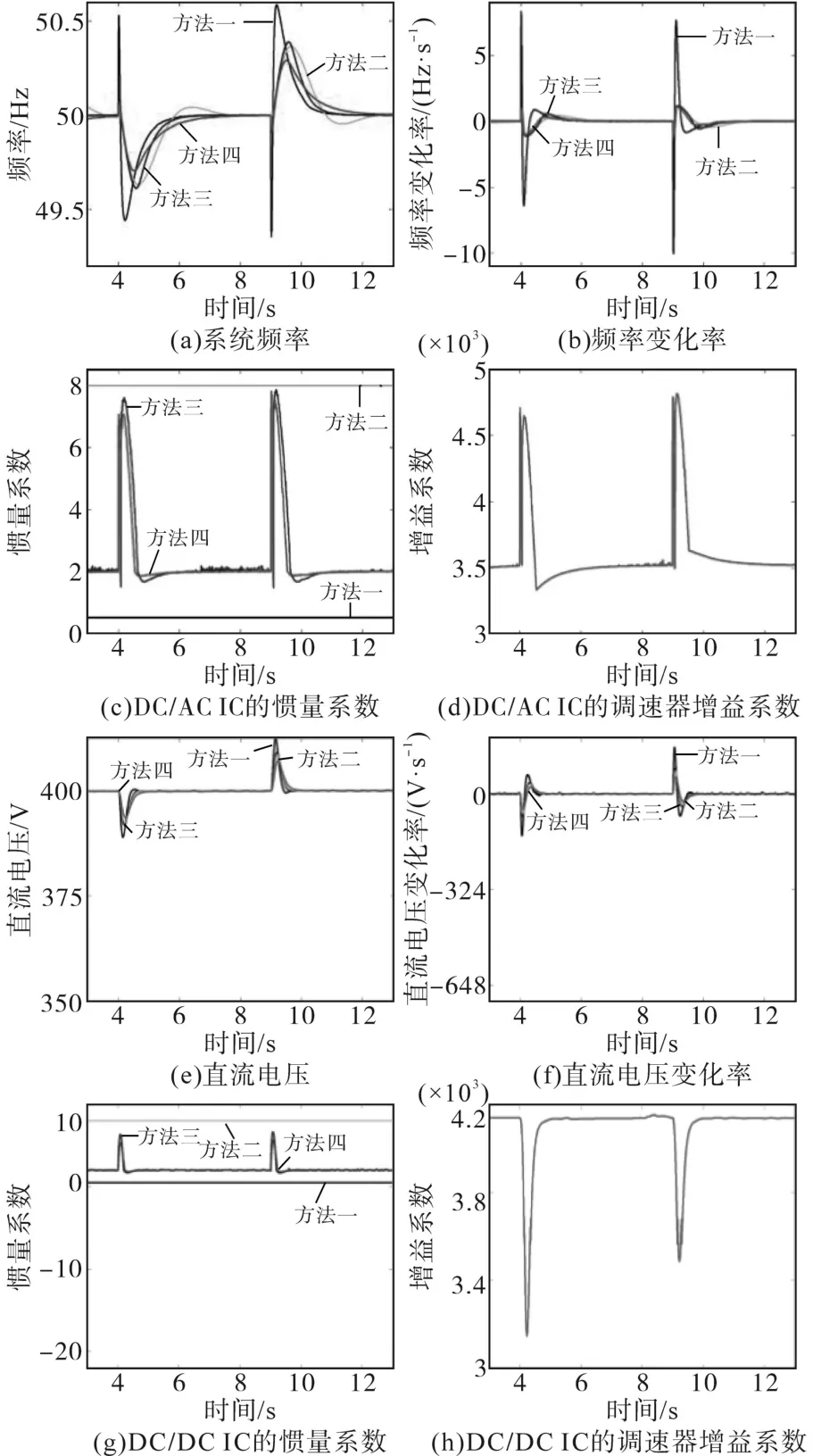
图4 不同控制方法下惯性和调速器增益在负载变化时对交流侧和直流侧的影响Fig.4 Effects of inertia and governor-gain response of the proposed control strategy on AC-side and DC-side under load changes
由图4可知,4种方法的控制效果有明显差异。图4a和图4e表明惯量很小时,反弹速度非常快,而系统频率和直流电压的最小值均超过了正常范围,频率变化率和直流电压变化率均很大。当惯量较大时,频率、直流电压、频率变化率和直流电压变化率的最低值均较高,但低于小惯量常数的方法,然而反弹速度非常慢,且存在振荡。在应用自适应虚拟惯量法时,虽然频率、直流电压、频率变化率和直流电压变化率的最低值稍微降低,但高于大惯量常数的方法。该方法消除了系统的振荡,改善了系统的动态性能。4种控制策略相比,采用自适应虚拟惯性和虚拟调速器增益控制的总体性能最好。
除了动态频率和直流电压的稳定外,合理的功率分配也是接口变流器的重要控制目标。图5为不同控制方法下系统功率分配情况图。

图5 不同控制方法下系统功率分配情况图Fig.5 Power allocation of the system under different control methods
由图5可知,0 s—4 s时,直流微网的输出功率约为8 kW,等于交流微网的输出值;4 s—9 s时,直流微网的输出功率约为14 kW,交流微网也是如此;最后,两个微网的输出功率仍然大致相等。因此,在测试交流/直流微网之间可以实现精确的功率分配。在功率的动态响应方面,由图5可知,应用大惯量控制时,交流微网的输出功率存在振荡。应用自适应惯量控制方法,不仅可以消除功率振荡,而且可以使交流微网的输出功率平滑。此外,如图5a和图5b所示,采用本文所提方法可以获得交流微网和直流微网最平稳的输出功率,具有良好的功率振荡阻尼功能。另一方面,如图5c所示,采用本文控制策略的接口变流器传输有功功率最优,即不仅不存在功率振荡,而且在扰动时刻可以快速提供较大的功率来抑制频率变化率和直流变化率。
4 结论
本文提出了一种功率管理方法,可以在保证适当功率分配的情况下,提高网格状交直流微网的频率和直流电压稳定性。该方法包括功率分配控制器、自适应虚拟惯量和虚拟调速器增益。此外,本文还对采用上述控制策略的网格状交直流微网进行了小信号稳定性分析,以指导控制参数的设计和选择。最后,通过仿真对上述控制策略的有效性进行了验证。
