基于遗传算法的PMSM简化转速控制策略

刘萌萌，李瑞芳，苗炜丽

（1.郑州理工职业学院机电工程系，河南 郑州 451150；2.郑州工业应用技术学院机电工程学院，河南 郑州 450000）

永磁同步电机（permanent magnet synchronous motor，PMSM）目前已得到了广泛应用，但PMSM驱动控制仍持续成为研究热点[1]。

PMSM控制方案设计时应在面对变化的负载曲线和不确定动态时确保其最佳性能和稳定性。磁场定向控制（field oriented control，FOC）首次于文献[2]中提出，目前已发展为标准化电机控制方案。为提升动态性能，文献[3]中首次提出了直接转矩控制（direct torque control，DTC），也发展为一种流行的控制方案。随着实时控制芯片技术的发展，计算密集型PMSM控制策略也被相继提出。文献[4]设计了一种基于扰动观测器的PMSM滑模控制器，但滑模可引起抖振。文献[5]对PMSM的模型预测控制策略开展了研究，文献[6]将离散空间矢量调制融入模型预测控制实现了恒定开关频率。但模型预测控制中控制动作的确定需要大量的计算，且对模型参数依赖。文献[7]针对PMSM系统自身非线性环节，设计了反馈线性化转速控制器。文献[8]则提出了PMSM的自适应控制。但这些控制方案中，未涉及系统非建模动态，而实际应用中，诸如温度和噪声等因素本质上不可预测，但仍会干扰控制过程。另一方面，软计算控制技术也在电机驱动控制中得到了应用[9]，但其计算成本较高[10]，使得实际实现难度较大。

综上，本文设计了一种基于遗传算法的PMSM简化转速控制策略。新控制方案规避了旋转坐标运算，降低了计算负担，且无需依赖电压或电流传感器，提高了可靠性。目前，对PMSM进行直接电压控制的主要方式为V/f控制，但性能欠佳[11]。而新方案中直接电压控制器的增益采用遗传算法优化，可实现最小电流损耗。

1 PMSM数学模型

PMSM在d-q坐标系下的数学模型可表示为

式中：ud，uq，id，iq分别为d，q轴定子电压和电流；Ld，Lq分别为d，q轴电感；R，Ψ，J分别为电枢电阻、磁链和转动惯量；p为极对数；ω，τ，τF和τL分别为机械转速、电磁转矩、摩擦转矩和负载转矩。

假设PMSM非线性系统的动态未知，并仅将ω和转子位置角θ作为系统可测量状态，则控制器设计目标可描述为提出一个控制律来迫使电机转速ω跟踪预定的随时间变化的参考值ω*，则电机参数Ld，Lq，R，Ψ，p，J，τF和τL也被假定为未知量。设eω=ω-ω*为电机转速误差，控制律输出为α，β轴电压uα和uβ，然后馈送到脉宽调制模块，以生成逆变器最终需要的占空比信号。忽略R的压降，稳态时定子电压幅值u和相角Δθ如下式所示：

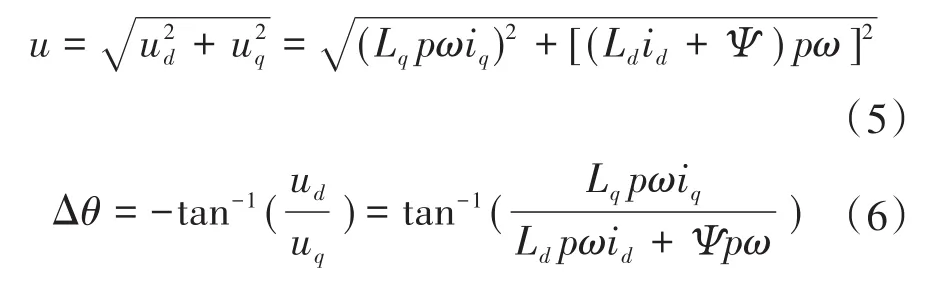
2 PMSM简化转速控制器设计

若无电流角控制，负载转矩的引入会导致过多的损耗产生，而控制d轴电流id=0则可实现最大转矩电流比（maximum torque per ampere，MTPA）控制，此时有：

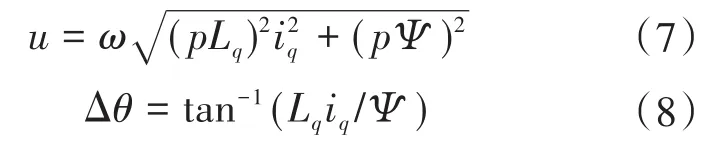
将id=0代入电机模型可推导得：

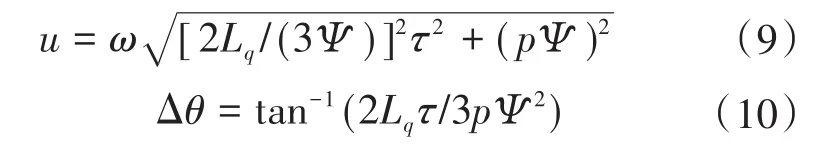
式（9）揭示了在空载时（τ=0）施加的电压幅值与电机转速之间的线性关系。此时，u=Kω，Δθ=0，斜率K=pΨ。但随着转矩的增加，斜率K平缓的坡度将逐渐变陡。对于具有显性转子的内置式PMSM，可通过d，q轴电流的某种组合实现MTPA。为了最小化定子电流，需相对于电流角取转矩的导数，这会导致更为复杂的系统动态。此时可通过数值求解出u，Δθ，ω和τL之间的关系，如图1所示。

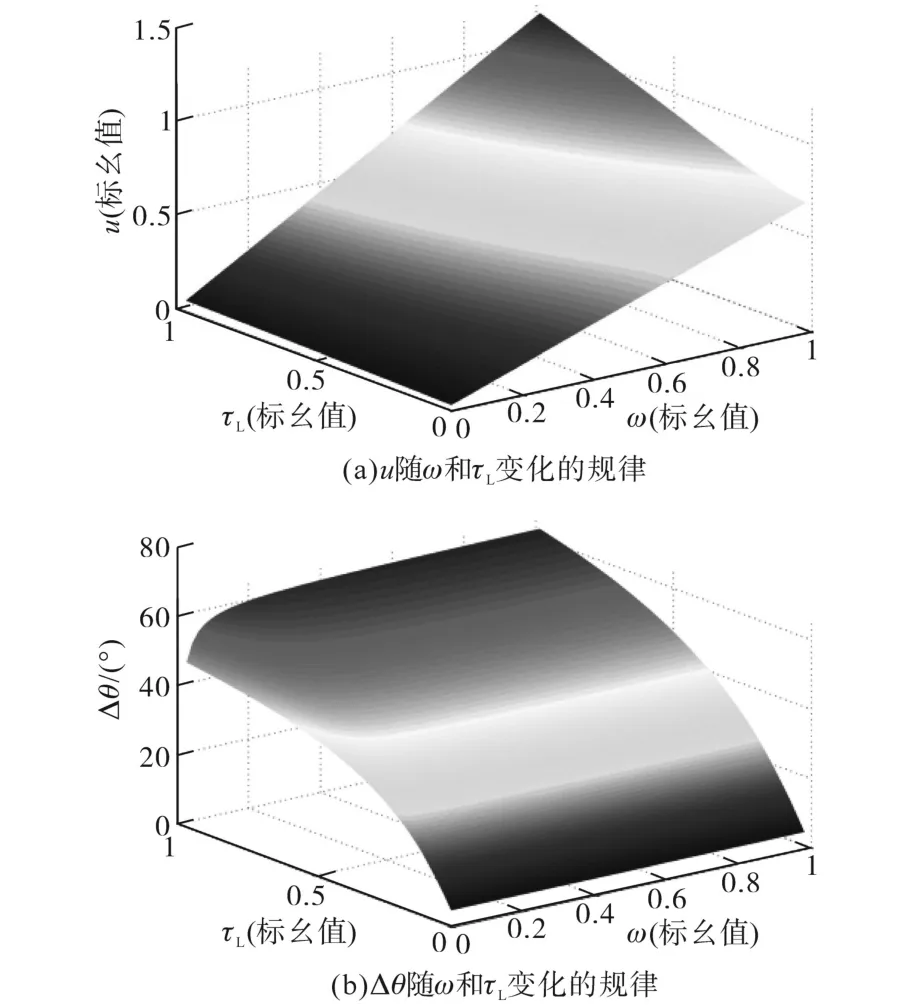
图1 MTPA中u和Δθ随转速和负载转矩变化的规律Fig.1 Law of u and Δθ changing with speed and load torque in MTPA

需注意的是，由于参数小扰动将导致明显的Δθ偏差，故不能依赖于电机参数的精确值实施应用。另外，转矩不能直接测量，因而考虑使用简单的PI调节器来近似：

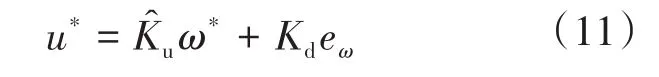
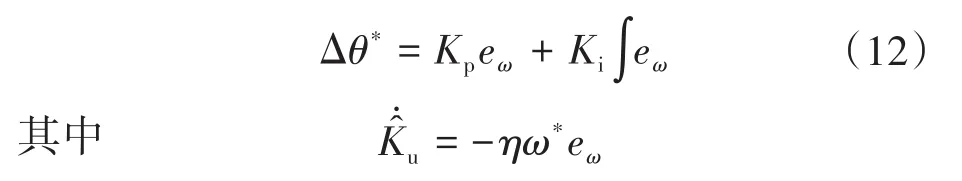
式中：u*，Δθ*分别为电压幅值和相角控制量；Kd为恒定增益；Kp，Ki分别为比例和积分增益；η为正常数增益，η决定了收敛速度。

α-β坐标系下电压控制量可写成：

式中：θu为α轴至施加电压矢量的角度。

在没有电流检测的情况下，文献[12]指出低功率因数运行下PMSM会产生更高的能耗。根据MTPA的特性，存在一组u和Δθ，使得电流带来的损耗最小。因此，自适应控制律需选择合适的控制增益Kp，Ki，Kd和η以获取最优的u*和Δθ*，但这并非易事。而遗传算法能够为可能受到不确定性扰动影响的系统提供非常好的近似，且具有自适应搜索能力，故非常适合于处理该问题。

图2所示为遗传算法实施的流程图，具体步骤如下：

图2 遗传算法流程图Fig.2 Flow chart of the genetic algorithm

第 1步：生成n组初始参数集合（Kp，Ki，Kd，η），并对应编码成染色体格式。

第2步：不同染色体对应参数集代入离线PMSM驱动系统模型中运算得到n组（eω，I），其中，I为电流幅值。

第3步：将n组（eω，I）代入遗传算法中适应度函数fcost进行评估。考虑需实现MTPA，同时还要保证精确的转速跟踪控制，故遗传算法中适应度函数fcost定义为速度误差积分和电流积分的加权和，即：

式中：ρ为权重系数，其定义了转速跟踪和MTPA之间的折衷。

第4步：判断是否存在控制器最优增益，若存在，则结束算法；若不存在，则由选择算子选择最优的两条染色体，即选择最优两组参数。

第5步：由交叉算子进行后代染色体（新参数集合）生成。

第6步：若n为奇数，则由突变算子生成新的染色体，并跳转至第2步重复执行，直至结束。

控制器的初始参数集合可通过从大量经验对象开始，然后以足够多的迭代次数运行优化来获得，但也将带来较大的计算量，因此基于离线过程完成，不作为实时控制周期的一部分，从而避免了给实时控制芯片带来繁重的计算负担。染色体个体被编码为16位，这在计算量和精度之间提供了很好的折衷。同时，将种群的初始染色体个体数量设置为15，以便快速收敛到最优解。

图3为基于遗传算法的PMSM简化转速控制器框图。

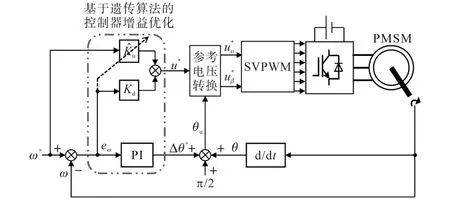
图3 基于遗传算法的PMSM简化转速控制器框图Fig.3 Block diagram of the simplified speed control strategy based on genetic algorithm for PMSM

3 实验验证及结论

为验证PMSM简化转速控制器性能，在PMSM驱动测试平台上开展了实验研究，测试平台主要由测试用PMSM，750 V直流源、10 kW逆变器（三相两电平拓扑，功率开关器件为IGBT）、7.5 kW感应电机（作为负载）、RTLAB实时仿真系统和转速测量旋转变压器等组成。其中，PMSM的参数如下：额定功率Pn=7.5 kW，额定转速ωn=1 800 r/min，额定转矩τn=39.5 N·m，d轴电感Ld=0.022 1 mH，q轴电感Lq=0.091 1 mH，定子电阻R=0.651，极对数p=2，转动惯量J=0.1 kg·m2，永磁磁链Ψ=0.670 9 Wb。控制器主要参数为：开关频率fsw=1 kHz，采样频率fsa=20 kHz，由遗传算法确定控制器增益为Kp=6.5×10-3，Ki=1.1，η=4×10-13和Kd=2.3×10-3。

图4和图5为转速参考ω*从0斜坡升至1 800 r/min后突加22 N·m负载转矩的测试结果，对比图4a和图5a中转速波形可看出，新控制器较传统FOC在负载转矩扰动时的转速响应更快，且电机定子电流幅值仍和FOC一样，保持在10 A以内，见图4b和图5b，即两者的稳态性能基本相似。从图4c和图5c中电机输出电磁转矩波形对比可看出，传统FOC方案下电机输出电磁转矩在负载扰动下易产生振荡，而新方案输出电磁转矩更平滑，抗扰能力更强。引入误差绝对值积分IAE和时间误差绝对值积分ITAE如下：

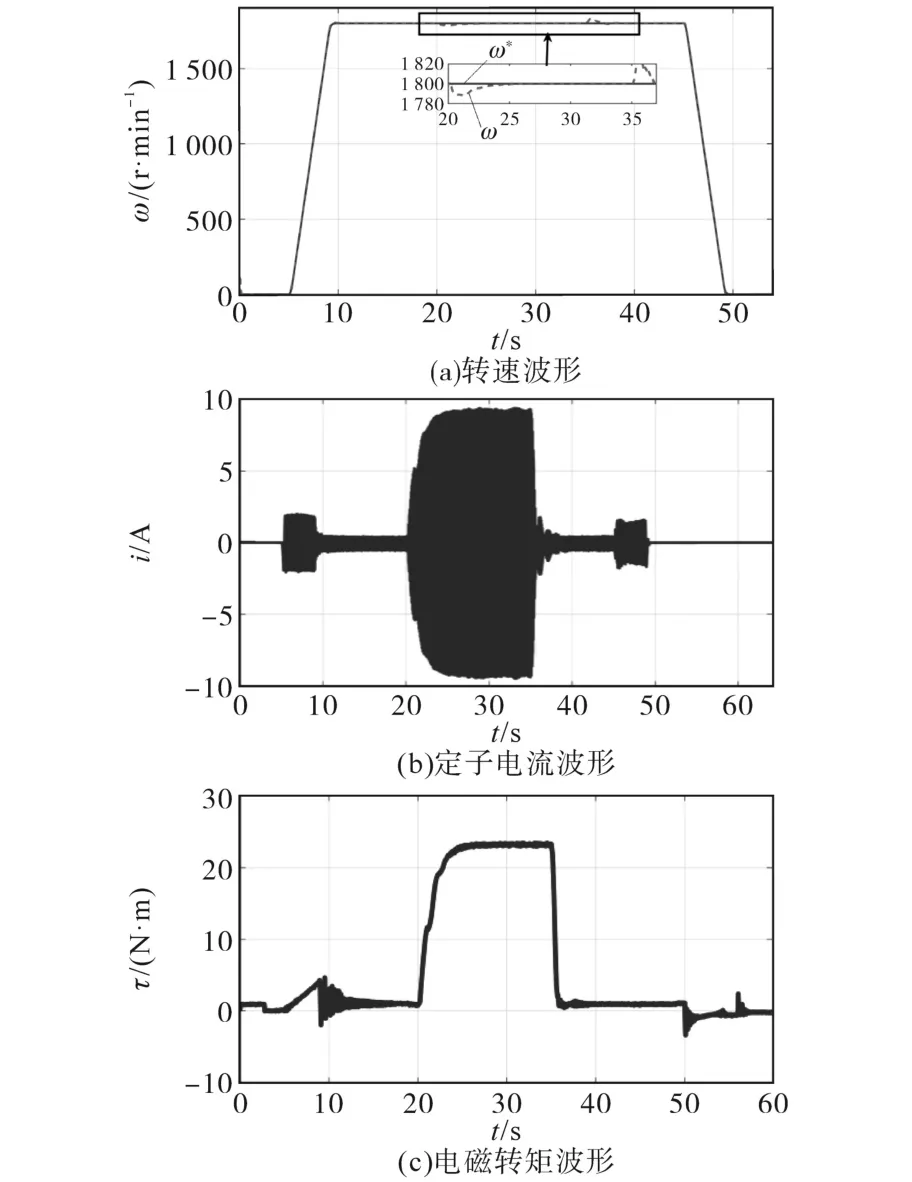
图4 负载转矩为22 N·m时传统FOC方案的测试结果Fig.4 Test results of traditional FOC scheme when the load torque is 22 N·m

图5 负载转矩为22 N·m时新方案的测试结果Fig.5 Test results of new scheme when the load torque is 22 N·m

式中：t0，tf分别为积分初始和终止时刻。

由图4和图5可计算出，传统FOC方案下IAE和ITAE分别为0.68和4.83，而新方案下IAE和ITAE分别为0.52和3.37，这验证了新控制器转速跟踪性能更好。

进一步，进行了ω*从0斜坡升至1 800 r/min后突加13 N·m负载转矩的测试，结果如图6和图7所示。

图6 负载转矩为13 N·m时传统FOC方案的测试结果Fig.6 Test results of traditional FOC scheme when the load torque is 13 N·m

图7 负载转矩为13 N·m时新方案的测试结果Fig.7 Test results of new scheme when the load torque is 13 N·m

与图4和图5中结果类似，新方案取得了和传统FOC方案相同的稳态特性，同时还具有更好的抗扰性和更快的动态响应。

最后，为了证明所提控制策略在不同工况下的有效性，进行了复杂工况测试，具体为：ω*从0斜坡升至500 r/min，稳定后负载转矩则以5 s的间隔分别施加5 N·m和15 N·m，再将ω*升至1 000 r/min，并施加相同转矩扰动，实验波形如图8所示。图中测试结果表明，新控制器在复杂工况下具有和传统FOC方案一样的转速跟踪性能，且电流消耗接近MTPA。

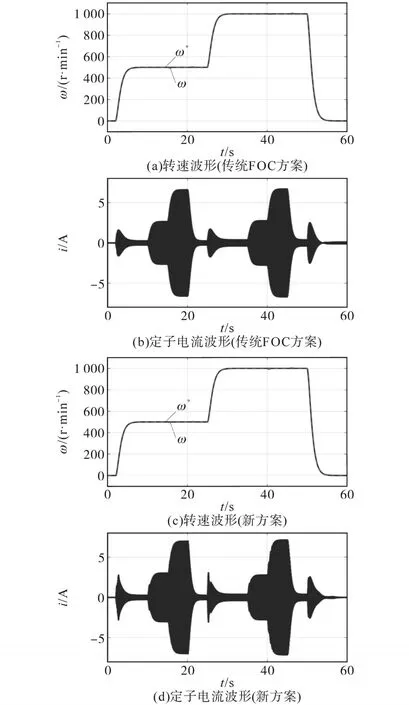
图8 复杂工况下的测试结果Fig.8 Test results under complex operating conditions

为优化PMSM控制器结构，本文提出了一种基于遗传算法的无电流传感器PMSM简化转速控制器。

新控制器不使用电流闭环调节，且不依赖于电机参数，可靠性较高。相对于传统的级联控制器架构，新方案采用直接电压控制，并利用遗传算法离线确定了最优电流损耗的控制增益，可实现最大转矩电流比。通过各类型工况下与传统FOC控制器的对比测试，验证了新方案具有与传统FOC方案类似的稳态性能，而动态性能和抗扰性更是稍优。新方案计算负担小，对实时控制芯片要求更低，故可成为PMSM低成本驱动器的理想控制策略。