基于虚拟同步电机的微电网二次调频技术

逄林 ，陆欣，武占侠，王学良，付美明，张洪明

（1.深圳市国电科技通信有限公司，广东 深圳 518000；2.清华大学电子工程系，北京 100084）

由于新能源的开发和应用是解决能源短缺和环境污染问题的重要途经，风能、光伏和潮汐能等得到了广泛关注[1-2]。新能源的利用必须首先借助发电技术将它们转换为电能，然后在当地直接使用或进行并网传输，构成微电网系统。对于微电网而言，发电侧为直流电源，需要利用电力电子逆变器将直流电变为三相交流形式，在此过程中，逆变控制算法也是保证发电质量的关键[3-4]。

传统的微电网逆变控制包括恒功率控制[5]、恒压频控制[6]和下垂控制[7]。恒功率控制根据有功和无功参考值产生恒定的有功和无功功率，属于完全被动的控制方式，无法为微电网提供任何电压或频率支撑；与恒功率控制不同，无论功率如何变化，恒压频控制时刻保证输出电压和频率稳定在额定值；对于频率调节过程，下垂控制分为有功—频率（P—f）和频率—有功（f—P）两种，而对电压调节过程，下垂控制可以通过无功—电压（Q—V）和电压—无功（V—Q）控制方法实现。下垂控制通常采用单环控制结构，其中，P—f和Q—V下垂控制采用功率反馈型结构，而f—P和V—Q下垂控制与之相反，为频率和电压反馈型结构。传统的微电网控制方法具有响应快、延时低的特点。当负载功率变化后，逆变器输出会迅速跟踪负载变化，导致输出电压和频率发生波动。这说明基于传统控制的电力电子逆变器具有惯量低与阻尼小的特性，大负载突变可能会使电网频率和电压偏离许可范围，给系统带来潜在风险[8]。

与传统逆变算法相比，虚拟同步机（virtual synchronous generator，VSG）概念的提出解决了微电网惯量低与阻尼小的问题，可以为电网提供强大的频率支撑[9-11]。VSG工作机理如下：频率调节采用双环控制结构，外环采用基于频率反馈的f—P下垂控制器，内环通过模拟真实同步发电机转子运动方程并利用功率反馈实现功率调节。转子运动方程中含有惯量和阻尼两个参数，通过设置不同值，便可赋予微电网与同步发电机类似的惯量与阻尼特性，降低系统动态性能[12]。然而，需要注意的是，虽然VSG控制能够降低负载扰动对频率特性的影响，提高频率稳定性，但它仍属于频率一次调节，无法消除稳态误差。在实际应用中，负载变化后，频率响应速度与频率偏移虽然会因VSG技术的应用得到抑制，但却无法稳定在额定值，且负载功率偏差幅度越大，稳态误差越大。

在传统电力系统频率控制中，消除一次调频稳态误差的过程被称为二次调频[13]，它需要控制发电装置输出更大的有功功率，从而使负载引起的频率偏移保持在额定值附近。参考传统电力系统二次调频机理，一些文献已经开展了针对基于VSG控制的微电网二次调频研究。文献[14-15]将PI控制器替代了f—P下垂控制器，但存在以下问题：PI控制器在功率稳定或波动很小时仍需要工作，但由于PI控制器具有延时作用，导致频率和功率调节速度降低；文献[16]将积分环节与发电机转子运动方程相结合，构建了二阶控制器，并且设计了只在需要时才执行频率二次调节的过程，更加符合电网工作需求，但是该结构已经完全摒弃了VSG理论的基础，无法体现VSG控制的优势。

针对上述问题，本文提出一种改进的基于VSG的微电网二次调频技术。首先，保留传统VSG控制结构，将频率控制误差经过PI控制器后自动产生前馈功率补偿；其次，定义频率偏移界限fthr的概念，当系统稳定后，若频率偏移超过fthr，则执行二次频率调节算法，增加微电网功率输出，使频率恢复至额定值。仿真和实验结果证明了该控制策略的可行性与有效性。

1 VSG一次调频机理

图1为基于VSG控制的微电网结构框图。图中，Udc为直流电源；C为母线电容；Ea，Eb，Ec为电网电压；Lf，Cf分别为滤波电感和电容；PCC为公共连接点；f，fN分别为电网实际频率和额定频率；P，Q分别为有功和无功功率；PN，QN分别为额定有功和无功功率；VN为额定电压；ω，θ分别为发电机机械角频率和转子位置。图1中频率调节环节的具体实现过程由图2所示。可以看出，VSG一次调频包含有功功率控制内环和频率控制外环两部分，其中外环采用f—P下垂控制器，内环采用同步发电机机械方程进行功率调节。下面对VSG一次调频的各部分进行介绍。

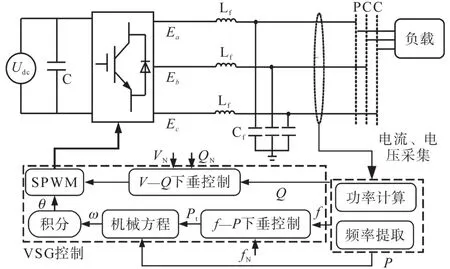
图1 基于VSG控制的微电网结构框图Fig.1 Microgrid structure based on VSG control

图2 一次调频结构框图Fig.2 Structure of primary frequency regulation

1.1 f—P下垂控制器

f—P下垂控制器是根据同步发电机频率和有功功率之间的下垂关系（如图3所示）所建立的，其本质为比例环节，当负载功率由PN变化至P1或P2，系统重新稳定后，工作频率也由fN变化至f1或f2。因此，通过可测量的实时频率值f求得微电网在新状态下需要输出的功率Pt：

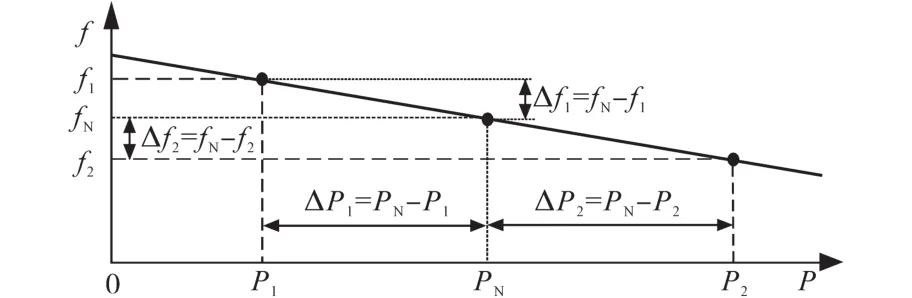
图3 同步发电机频率—有功功率下垂关系Fig.3 Droop relationship of synchronous generator between frequency and active power

式中：kf为下垂系数。

1.2 机械方程

机械方程是根据同步电机物理意义建立的，将下垂控制器的输出Pt作为发电机的输入机械功率，并将电网实时有功功率P作为电机的电磁输出功率，模拟同步发电机的转子运动方程为

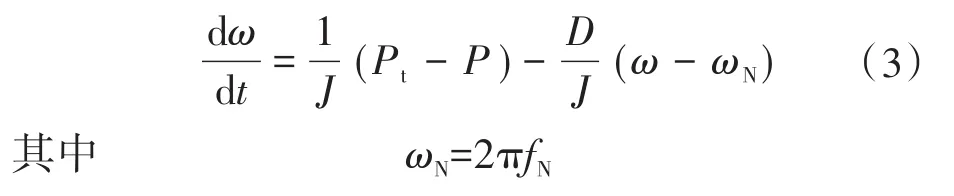
式中：J为虚拟惯量；D为虚拟阻尼；ωN为电网额定角频率。

另外，对发电机机械速度积分，可得到用于产生调制波的转子位置角度θ，即

根据前述频率调节过程，VSG调频机理如下：当负载功率偏离额定值后，系统频率随之变化，此时，利用下垂控制器以及频率偏移量可求得所需要输出的有功功率，令其作为功率参考值，并连同微电网实时功率输入至同步电机机械方程，由于机械方程是一阶惯性环节，功率响应速度会降低，使频率波动得到抑制。然而，虽然系统动态响应速度降低，系统所输出的功率仅能使系统频率维持在新的平衡状态，不能恢复至额定值，因此需要二次频率调节来减小稳态误差。

2 改进的VSG二次调频方案

2.1 电力系统二次调频原理

二次调频概念来源于传统电力系统，主要是针对变动幅度较大或者周期较长的负载扰动。电力系统二次调频过程如图4所示，图中，PG为发电机带有一次调频时的有功功率静态频率特性，PL为负荷有功功率静态频率特性。起始阶段，电网工作在额定点（N），当负载功率由PL突变至PL′（A点）后，若仅采用一次调频，系统最终会稳定在N′，此时功率和频率记为P′和f′，频率偏差会比较大；此时，若系统具有可调节频率，可手动或自动控制发电机原动机的调频器，使得发电机原动机输出的机械功率增加至B点，当系统再次稳定后，系统工作在N"点，此时功率和频率分别为P"和f"，显然，f"与fN的偏差小于一次调频后的频率偏差。需要说明的是，二次调频可增加的机械功率与系统有关，若二次调频时发电机原动机输出的机械功率相应增加量等于负荷初始变化量，系统频率将不会发生偏移，实现无差调节。

图4 电力系统二次调频过程Fig.4 Secondary frequency regulation for power systems

2.2 基于VSG的二次调频方案

根据电力系统二次调频过程，其主要特征可以总结如下：1）适用于大波动或长周期波动负载，此时频率偏移明显；2）对于小波动或短周期波动负载，频率偏移较小，能够维持在安全运行区间，二次调频可以不用；3）二次调频的实现依靠改变发电装置的输出有功功率。

参考电力系统二次调频过程，对于微电网而言，可通过功率补偿算法改变逆变器输出以适应负载变化，本文提出了一种基于VSG的二次调频方案，如图5所示。图中，s为开关，fthr为最大许可频率偏移界限，我国对于大电力系统的频率偏差规定不得超过±0.2 Hz，本研究中fthr取0.2，实际中，为进一步保证系统安全性，fthr可取更小值。

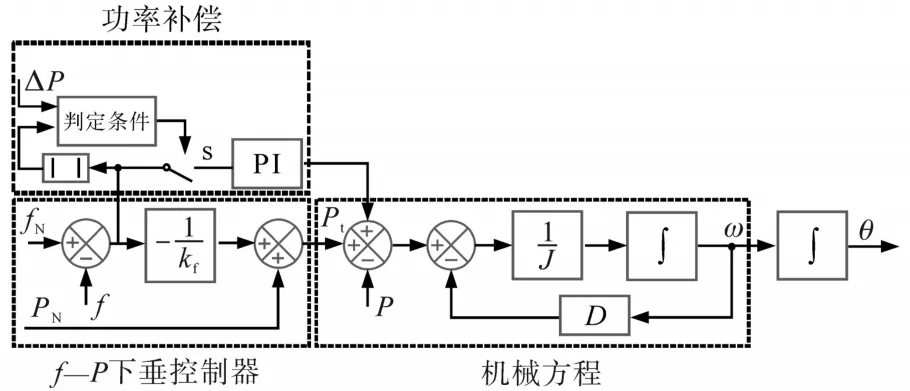
图5 基于VSG的二次调频方案Fig.5 Secondary frequency regulation scheme based on VSG

所提出的二次调频方案执行过程如下：

1）任何情况下，f—P下垂控制器和同步电机机械方程都进行微电网频率一次调节。

2）检测额定频率与实时频率偏差fN-f以及额定有功功率与实时功率偏差ΔP（即PN-P），将它们偏差绝对值作为是否启动二次调频的判定条件，其中，判定条件执行过程为：当频率偏差小于fthr且前一工作周期内未触发二次调频，开关s断开，仅采用一次调频程序实现系统控制；当频率偏差大于fthr且|ΔP|≠0，s闭合，启动二次调频操作；当触发二次调频后，若负载功率没有恢复至额定值（即|ΔP|≠0），s闭合，持续执行二次调频程序，当且仅当负载功率恢复到额定值时，断开开关s。

3）当s闭合后，额定频率与实时频率偏差经过PI控制器自动计算出所需要补偿的功率，与Pt相加后作为机械方程的参考功率。

所提出的基于VSG的二次调频方案具有以下优点：首先，保留了VSG控制的本质结构，即机械方程没有修改，理论更加明确；其次，完全参考电力系统二次调频的过程，仅在频率偏移量较大时执行二次调频操作，在无负载波动时，PI控制器不执行，以保证良好的动态性能。

3 仿真与实验验证

为全面验证本文所提二次调频方法的有效性，对两个案例分别进行仿真和实验验证。

3.1 仿真验证

用于仿真验证的微电网系统参数如表1所示。此外，PI控制器参数由试凑法获得，比例因子kp=3，积分因子ki=100。利用Matlab/Simulink搭建系统模型，为全面验证所提二次调频方法的有效性，仿真从以下两个方面展开：1）突加负载。系统带额定负载启动，在0.5 s突加1 kV·A有功功率负载（小幅度负载扰动），在1.0 s再突加3 kV·A负载（大幅度负载扰动），直至1.5 s结束；2）突降负载。系统带额定负载启动，在0.5 s突降1 kV·A负载，在1.0 s再突降3 kV·A负载，仿真在1.5 s结束。最后记录并分析仿真结果。

表1 仿真用微电网系统参数Tab.1 Parameters of microgrid used for simulation

图6为突加负载时的微电网性能曲线图。系统启动后，有功功率和频率维持在额定值；在突加1 kV·A负载后，功率迅速跟踪至负载值，在VSG一次调频控制下，频率在50 ms内降低至49.94 Hz，稳态时频率偏移量为0.06 Hz，小于许可频率偏差，系统仍处于安全状态；在1 s时，有功功率迅速上升至14 kV·A，频率开始下降，但当频率低于49.8 Hz后，在二次调频算法的控制下，系统频率迅速回升，且在400 ms后维持在额定值。需要说明的是，控制过程中，频率最小值为49.78 Hz，略低于49.8 Hz，这是由于VSG控制及PI控制器调节具有延时作用导致的，但考虑到调节时间很短，能够保证系统处于较为安全状态；此外，可以看出一次调频响应速度远远大于二次调频速度，说明本文设计的开关s对保证系统的动态性能具有重要意义。

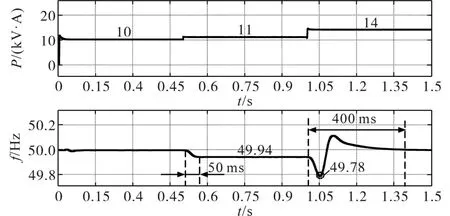
图6 突加负载微电网工作特性Fig.6 Working performance of microgrid with sudden load imposed

图7为突降负载时的微电网性能曲线图。与图6一样，在1 s之前，系统采用一次调频算法，频率响应速度比较快，当突降1 kV·A负载时，仅用40 ms系统频率上升并稳定至50.06 Hz；当突降3 kV·A负载后，频率迅速上升，当频率偏移量超过0.2 Hz后，二次调频算法执行，频率恢复至50 Hz。仿真结果表明，所提出的基于VSG的二次调频技术能够令微电网频率偏移量在许可范围内，保证系统安全。

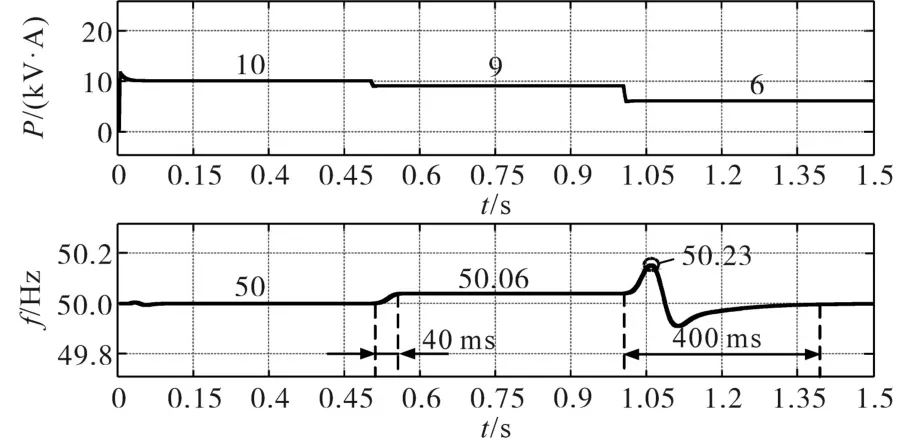
图7 突降负载微电网工作特性Fig.7 Working performance of microgrid with sudden load reduced

3.2 实验验证

为了通过实验验证所提出的基于VSG的二次调频算法，搭建了一套低压测试平台，系统参数如表2所示，PI控制器比例因子kp=0.5，积分因子ki=30。逆变控制算法在DSP TMS320F2812内执行，测试也包含突加负载和突降负载两种模式，测试过程如下：当系统稳定地工作在额定状态后，在0.5 s突加/降负载60 V·A，在1.0 s时结束实验，记录并分析实验结果。

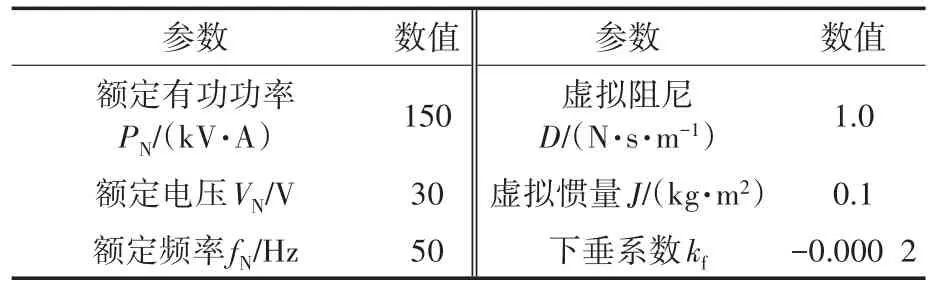
表2 实验用微电网系统参数Tab.2 Parameters of microgrid used for experiment

图8和图9分别为突加负载和突降负载时微电网的有功功率和频率特性曲线。

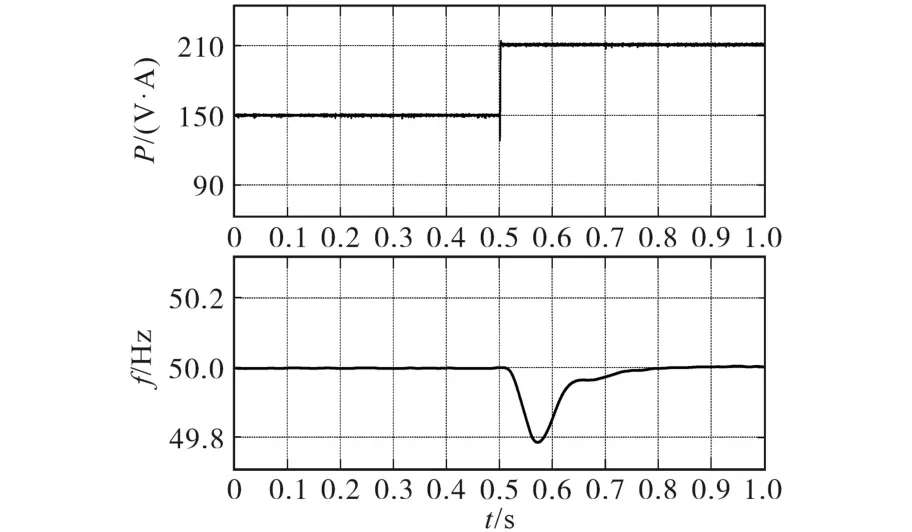
图8 突加负载微电网工作特性Fig.8 Working performance of microgrid with sudden load imposed

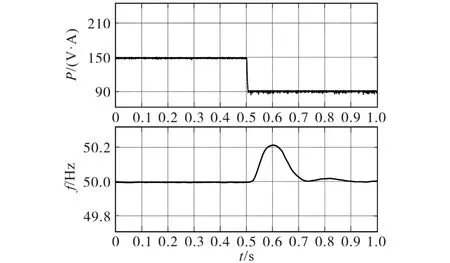
图9 突降负载微电网工作特性Fig.9 Working performance of microgrid with sudden load reduced

从实验结果可以看出：首先，与仿真结果相比，图8和图9中频率波动略大，这是由于系统工作频率不同导致的。其次，当系统突加相同负载时，频率特性与突降负载时的频率特性并不完全一致，具体体现在：

1）图8中频率下降速度很快，但是当二次调频算法执行时，频率恢复速度比较慢，相比之下，在负载突降后，图9中频率上升速度比较慢，但是恢复速度比较快；

2）当系统重新恢复至稳态后，图8中频率稳态性能要高于图9中结果，这是由于负载不同导致的。

整体而言，在负载突变后，所提出的基于VSG的二次调频方案依然可以令微电网频率工作在额定状态，保证系统工作在安全区间。

4 结论

本文的主要研究内容及贡献总结如下：

1）针对传统VSG控制在功率波动后具有稳态误差的问题，本文提出了一种改进型微电网二次调频技术。当面临大幅度负载波动时，通过PI控制器实现前馈功率补偿，所提出的二次调频技术没有改变VSG控制理论基础。

2）为满足电力系统二次调频规范，即仅在负载波动比较大时进行二次调频操作，定义频率偏移界限的概念，用来判断是否需要执行二次调频算法：当频率偏差较小时，只采用一次调频技术以保证系统响应速度；当频率偏差超过界限后，利用二次调频技术消除稳态误差。仿真和实验验证了所提方法的有效性。