三相高频AC/DC/DC变换器的宽频等效建模方法

张扬，高添 ，林卫星

（1.南昌工程学院机械与电气工程学院，江西 南昌 330099；2.特变电工新疆新能源股份有限公司，新疆 乌鲁木齐 830011）

三相高频AC/DC/DC变换器是交流到宽幅直流能量的变换装置，在新能源领域运用越来越广泛[1]。光伏逆变器、充电桩、储能变流器、风电变流器等常见电力电子设备都属于三相高频AC/DC/DC变换器[2-3]。由于三相高频AC/DC/DC变换器的工作特性，在开关器件快速通断过程中会产生高频谐波，而在传统的建模方法中往往忽略高频谐波分量，但此高频谐波分量却容易引起设备的振荡与不稳定，从而造成系统运行可靠性变差。

为了准确预测三相高频变换器中的高频谐波分量，提高设备的动态性与稳定性，充分发挥电力电子设备在新能源领域的优势，对三相高频变换器建模分析显得尤为重要[4-6]。目前，三相高频变换器的建模主要包含开关等效模型和小信号平均等效模型两大类。

传统开关模型考虑了各开关器件及电路状态的高频切换，更贴近变换器的实际工作情况，但开关模型不仅解析困难且是非线性模型，不利于系统控制；小信号平均模型是低频平均模型，虽然容易拓展到采用不同控制方法的开关变换器或分布式系统，但是其精确度只能满足低频准确，无法在高频电路中使用。因此，二者都不能准确预测设备中的高频谐波分量[7-8]。文献[9-11]提出了连续和非连续导通模式下高频变换器的开关模型，虽然通过该模型分析得到的电压电流波形与实际波形的跟随性较好、高频谐波预测误差较小，但是经开关模型得到的计算方程简化困难而且是离散型非线性的，不利于控制。文献[12-14]提出了高频变换器的小信号平均模型，虽然得到的微分方程是线性化的，电流、电压波形可控制，但小信号平均模型只能提供高频变换器在某一个稳态工作点的特性，并且忽略了高次谐波分量，与实际电路中存在的谐波分量差别较大，不适用于具有高次谐波的系统。

综上所述，本文提出一种具有通用性的三相高频AC/DC/DC变换器的宽频等效建模方法，该方法与传统方法相比，得到的电流、电压波形不仅是线性可控的，而且与实际电路中的波形保持较强的跟随性，能准确预测电路的高频谐波分量，所以可实时反映实际电路的工况，增强电路控制的精确性，提高运行的可靠性。

1 三相高频AC/DC/DC变换器的拓扑结构及传统等效模型

1.1 三相高频AC/DC/DC变换器的拓扑结构

图1为三相高频AC/DC/DC变换器拓扑结构图。如图1所示，拓扑图包含三相AC/DC电压源型变换器电路和DC/DC斩波电路。

图1 三相高频AC/DC/DC变换器拓扑图Fig.1 Topological diagram of three-phase high frequency AC/DC/DC converter

图1中，ik(k=1,2,3)为三相交流电流；ek(k=1,2,3)为三相交流电压；N为电压v+和v-参考地电网中性点；is为直流环节的电流；i0为滤波电容电流；vC0为直流电容电压；a，b和c点的电压v1,v2和v3为开关变量；L，r分别为三相AC/DC电压源型变换器的电感和电阻；uk为晶闸管状态，uk∈{-1,1},k=1,2,3；L1，R0分别为 DC/DC 斩波电路的电感和电阻；C1为DC/DC斩波电路的电容；vC1为DC/DC斩波电路的直流输出电压；H为DC/DC斩波电路的晶闸管；D为DC/DC斩波电路的二极管；u为DC/DC斩波电路的占空比。

1.2 三相AC/DC/DC变换器的传统等效模型

2 三相高频AC/DC/DC变换器的宽频等效模型

2.1 三相AC/DC变换器的宽频等效建模

2.2 高频AC/DC/DC变换器的宽频等效建模

开关函数如图2所示，n=1时晶闸管导通，n=0时晶闸管断开。

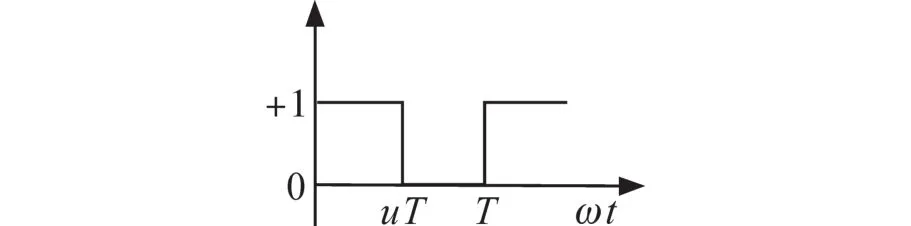
图2 开关函数Fig.2 Switch function

3 仿真与验证

3.1 仿真

为了验证所提等效建模方法的有效性和正确性，本文仿真和试验验证的设备参数如下：三相AC/DC线电压E=380 V（有效值），三相AC/DC电感L=40 mH，直流滤波电容C0=1 mF，DC/DC电路电感L1=1 mH，DC/DC电路电阻R0=10 Ω，输出滤波电容C1=100 μF，开关频率fS=3 kHz。

图3为三相AC/DC/DC高频变换器的整体框图，采用电压外环控制和电流内环控制[15-16]相结合的方式，电压外环控制采用PI调节控制得到电流d轴分量参考值。电流内环控制首先经过PLL锁相环锁住相角θ，再经过dq变换，得到d，q轴电流分量id，iq，结合参考值得到控制输入变量βd，βq，再通过dq反变换得到SPWM的控制输入βk，改变不同占空比进一步验证了所提等效模型的优越性。

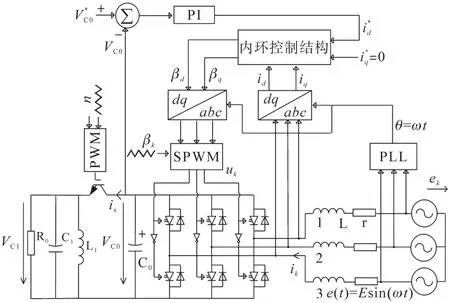
图3 整体框图Fig.3 Overall block diagram

AC/DC变换器输出直流电压VC0在600 V左右波动，其波形如图4所示。将VC0作为DC/DC斩波电路的输入电压，分别讨论u=0.3，0.5，0.7时所提模型与传统模型（开关、平均模型）的输出电压工况对比，不同状态下输出电压如图5所示。

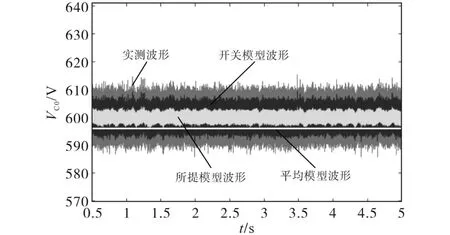
图4 三相AC/DC变换器输出电压Fig.4 Three-phase AC/DC converter output voltage

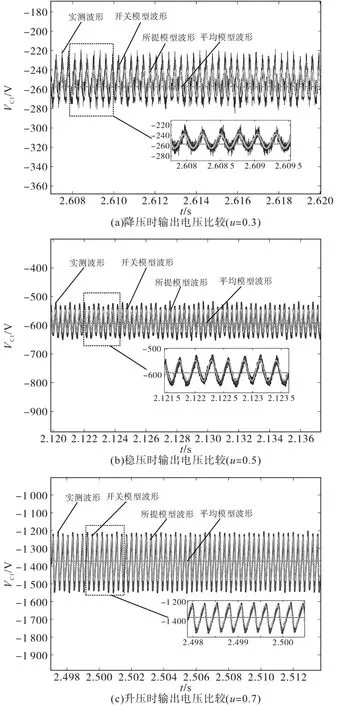
图5 不同状态时输出电压Fig.5 Different states output voltage

当u=0.3时，DC/DC斩波电路的输出电压VC1在-257 V左右波动，如图5a所示，表示所提模型输出电压与传统模型输出电压、实测输出电压的波形对比，斩波变换器工作在降压状态。

当u=0.5时，DC/DC斩波电路输出电压VC1在-600 V左右波动，如图5b所示，表示所提模型输出电压与传统模型输出电压、实测电压的波形对比，斩波变换器工作在稳压状态。

当u=0.7时，DC/DC斩波电路输出电压VC1在-1 400 V左右波动，如图5c所示，表示所提模型输出电压与传统模型电压、实测电压的波形对比，斩波变换器工作在升压状态。

3.2 试验

图6为实验样机取u=0.5时的试验波形，偏移量为-600 V。明显看出其含有高频纹波，且峰峰值大约80 V，此高频纹波易在器件上引起高频谐波。u=0.3，0.7时与之类似。

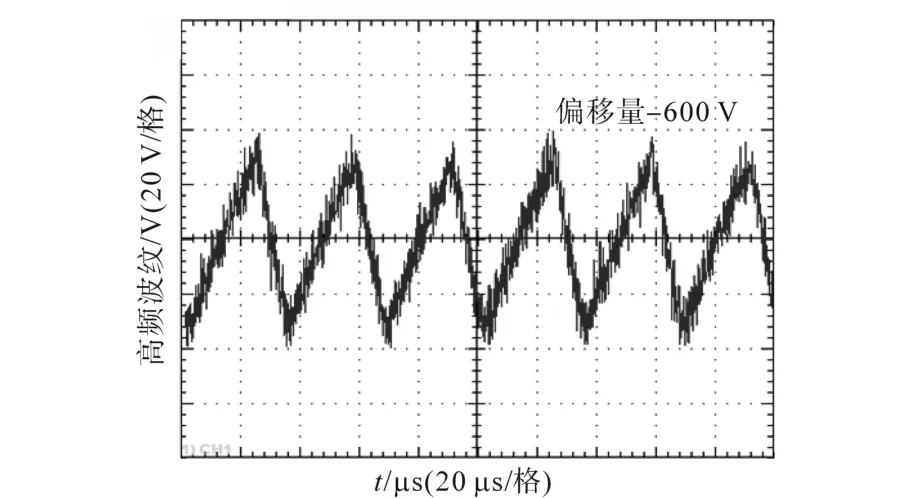
图6 u=0.5时实验高频纹波图Fig.6 High frequency ripple diagram when u=0.5

4 分析与讨论

通过傅里叶分析基波直流分量幅值Udc和3 kHz次电压谐波分量Uhar原理如下：

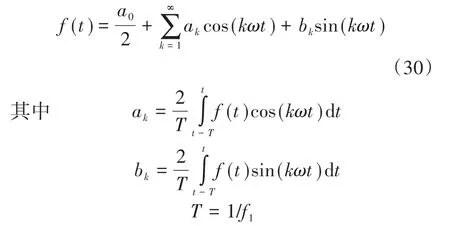
式中：T为基波周期；f1为基波频率。

由上述原理分析可得u为0.3，0.5，0.7时三种工况输出的基波直流电压幅值Udc和3 kHz次电压谐波分量Uhar如图7所示。

图7 不同状态下的傅里叶分析图Fig.7 Fourier analysis diagrams in different states

从图7各分图上部分图可知开关模型波形与实测波形一直保持良好的跟随性，平均模型输出基波电压幅值几乎与理论值无所差别，定义输出基波电压幅值偏差百分比计算如下：

式中：N%为输出基波电压幅值偏差百分比；Vav为平均模型输出基波幅值电压；Vtest为需要对比分析的模型输出的基波幅值电压。

从图7各分图下部分图分别可看出三种工况的3 kHz谐波分量，所提模型在u=0.3，0.5，0.7三种工况的3 kHz谐波分量都非常接近开关模型，偏差均在0.5 V以内，能有效反映真实电路的高频谐波分量，平均模型则无法反映高频谐波分量，所提模型可弥补此不足。

运用式（31）对比所提等效模型与开关模型在三种工况时的输出基波电压幅值偏差百分比如图8所示。由图8可知，所提模型的基波电压幅值更加接近实际电路值。

图8 电压幅值偏差百分比对比图Fig.8 Voltage amplitude deviation percentage comparison chart

5 结论

本文将传统的开关模型建模方法、小信号平均模型建模方法与所提的宽频等效模型建模方法对比，通过在Matlab/Simulink中仿真分析和试验可得：所提等效建模方法弥补了开关模型建模方法难以解析、输出方程非线性不可控的不足，且输出电压幅值偏差更小，更加接近真实工况电路；解决了小信号平均模型建模方法无法预测高频谐波分量的问题。运用所提等效建模方法可预测任意次高频谐波分量。

本文以3 kHz谐波分量为例，对三种工况的预测值与实际值偏差均在0.5 V的波动范围内。因此，所提建模方法能有效避免设备发生高频振荡，可提高设备控制的精确度，从而使系统更加可靠稳定地运行。