特征直连与结构化约束的多视图子空间聚类*

张翼飞，邓秀勤，王卓薇

(广东工业大学数学与统计学院,广东 广州 510006)

1 引言

多视图聚类通过数据的不同视图来学习数据包含的信息和结构，并由此对多视图数据进行簇划分。不同于传统的单视图数据聚类，多视图聚类面对的是更加复杂的数据。由于数据样本来源或者特征表达方式的多样性，多视图聚类需要面对的是如何通过多个视图来获取一个良好的聚类结果。

综上所述，由于多视图聚类算法的不断发展，子空间学习作为一个重要的方法已经被广泛应用。但是，现有的多视图聚类却忽略了原有的特征直连数据[15]，即将多视图数据每个样本对应的特征拼接起来得到的数据。尽管传统的聚类算法在特征直连数据上表现不好，但是特征直连数据对于聚类结果仍有一定的促进作用。此外，为了学习到合适的子空间表示，还需对子空间表示的结构进行探究，同时探寻特征直连数据与多个视图之间的差异性。因此，本文提出了基于特征直连和结构化约束的多视图子空间聚类算法FSMC(Feature concatenation and Structured constraints based Multi- view Clustering)。本文主要贡献可概括为：

(1)将特征直连数据加入算法框架，与原有的多视图共同学习，探寻多视图与特征直连数据的关系；

(2)通过子空间分解重构误差，保证误差的稳定性；

(3)通过正则化约束保证子空间表示的结构稀疏性。

2 相关工作

2.1 子空间聚类

在数据集X1∈Rm×n上共有n个样本，每个样本有m个特征，需要一个合适的子空间V∈Rn×n满足式(1)：

s.t.diag(V)=0

(1)

其中，‖·‖∂为范数表达式，∂为泛指，其可能取值为1，2,…，当∂=1时，式(1)为稀疏约束，当∂=*时，式(1)为核范数，此时为低秩约束，diag(V)为对角线上元素，diag(V)=0表明其对角元素全为0，该约束是为了防止出现平凡解。为了减少过拟合以及增加学习到的子空间的条件(稀疏或低秩)，通常会在式(1)的基础上添加约束项，那么式(1)变为式(2)[12]：

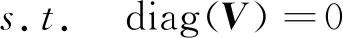
(2)

其中,‖·‖Ψ为范数表达式,Ψ与式(1)中的∂同为泛指，当Ψ=1时，式(2)为稀疏约束，当Ψ=*时，式(2)为核范数，此时为低秩约束。α为超参数，用于调节范数大小。

2.2 多视图子空间聚类

由于子空间聚类算法在多视图数据上的可扩展性，可将式(2)扩展为多视图子空间聚类算法。即对于具有v个视图的数据集X={X1,X2,…,Xv}，有：

(3)

其中,Vi为对应视图Xi下的子空间。在学习到每个视图下的子空间后，最简单的办法是通过求和取平均值来获得最终的共识矩阵，即:

(4)

研究人员通过各个视图所蕰涵的信息来更加合理地获得共识矩阵，则式(3)可改为式(5)[15]：

(5)

其中，S为共识矩阵，β为超参数。

式(5)不同于式(3)，其共识矩阵的获得是与子空间学习一起进行的，两者框架的统一能确保最终的共识矩阵更加合理。

3 特征直连与结构化约束

本节提出了一种基于特征直连与结构化约束的多视图子空间聚类算法FSMC。该算法通过特征直连数据与多视图数据的共同学习来重构误差，并通过约束使子空间满足特定的结构，同时还考虑了多个视图子空间与直连视图之间的关系。

3.1 特征直连

s.t.E=D-DV

(6)

其中，λ是超参数;E为误差矩阵;V为其相应的子空间表示;‖·‖2,1为矩阵的L2,1范数，表示对矩阵的行求向量的L2范数得到一个向量，然后再对该向量求L1范数。‖E‖2,1是为了重构误差，使误差趋于稳定，‖V‖2,1为结构化约束，保证子空间的稀疏约束。

3.2 结构化约束

为了稳定重构误差和保证子空间的稀疏约束，将式(3)所示的多视图子空间聚类基本公式修改为式(7)：

s.t.Ei=Xi-XiVi,i=1,2，…,v

(7)

为了将多视图数据与特征直连数据联系起来，将式(6)与式(7)动态结合起来得到式(8):

L=αL1+(1-α)L2

(8)

其中,α和1-α是各自的权重,分别代表多视图与直连数据的重要程度。通过为多视图数据与特征直连数据分配权重可以控制两者对于最终结果的影响程度。

在式(8)下，无法得到一个统一的共识矩阵，而且从直观意义上来看，特征直连数据与多视图存在着一定的联系，直连数据中指定大小的数据就可以表示成多视图中某一个视图的特征数据。因此，为了测试多视图各个子空间与直连数据子空间的相似性和差异性，需要通过正则化约束来进行学习。同时，为了获得一个最终的子空间表示，可以通过多视图子空间Vi与直连子空间V之和来得到最终的共识矩阵S。综上所述，可得公式(9):

s.t.diag(V)=0,diag(Vi)=0,

i=1,2,…,v,Ei=Xi-XiVi,E=D-DV

(9)

其中，γ为超参数;Ei为视图Xi的误差矩阵;S为需要学习的共识矩阵;β和γ为超参数;前2项为多视图与特征直连数据的子空间学习部分;第3项中的第1部分为多视图与特征直连数据的相关性和差异性约束，第2部分则是通过多视图与特征直连数据共同学习共识矩阵用作聚类。图1给出了FSMC算法的大致过程，其中，左边方框表示特征直连的实现方式，右边方框表示多视图子空间和特征直连子空间之间的差异性和共同性的学习，箭头指向表示其转换过程，如双向箭头表示4个子空间矩阵是相互影响的。

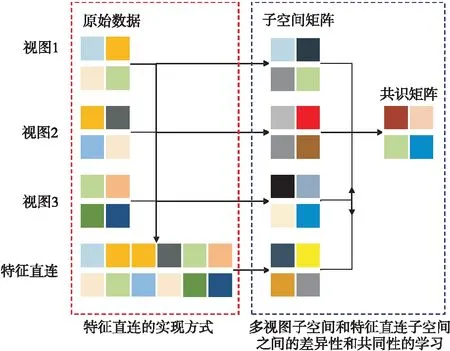
Figure 1 General process of FSMC algorithm

3.3 FSMC算法优化

对于式(9)的优化，需要引入多个变量，并采用增广拉格朗日迭代求解。引入变量Ci和C后式(9)变为式(10):

s.t.Ci=Vi,C=V,Ei=Xi-XiVi,

E=D-DV，diag(V)=0,

diag(Vi)=0,i=1,2,…,v

(10)

式(10)的优化步骤如下所示(其中，〈A,B〉为矩阵ATB的迹，A和B泛指矩阵)：

步骤1固定除Ei之外的所有变量，更新Ei，此时式(10)变为式(11)：

s.t.Ei=Xi-XiVi,i=1,2,…,v

(11)

由于每个视图都是独立的，那么式(11)可拆分并转换为式(12)：

(12)

其中,Yi为拉格朗日乘子，是与Xi具有相同行数和列数的矩阵;u为参数;Ei的更新公式[19]如式(13)所示:

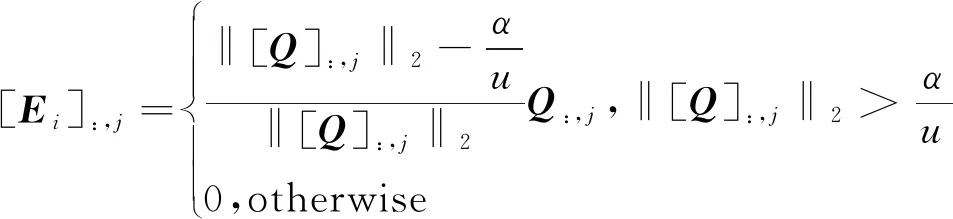
(13)

其中,Q=Xi-XiV+Yi/u,[Q:,j]表示矩阵Q的第j列元素，[Ei]:,j表示视图Xi的对应矩阵Ei的第j列元素。

步骤2固定除E之外的所有变量，更新E，此时式(10)变为式(14)：

(14)

其中Y是与E具有相同行数和列数的矩阵。式(14)的求解方式同式(12)。

步骤3固定除Ci之外的所有变量，更新Ci，此时式(10)变为式(15)：

s.t.Ci=Vi,i=1,2,…,v

(15)

类似于步骤1，式(15)可拆分并转换为式(16)：

(16)

其中，Yv+1是与V具有相同行数和列数的矩阵。式(16)的求解方式同步骤1。

步骤4固定除C之外的所有变量，更新C，此时式(10)变为式(17)：

(17)

其中，Y′是与C具有相同行数和列数的矩阵。式(17)的求解方法同上。

步骤5固定除Vi之外的所有变量，更新Vi，此时式(10)变为式(18):

(18)

因此，对式(18)求导可得更新式(19)：

Vi=(T1)-1T2

(19)

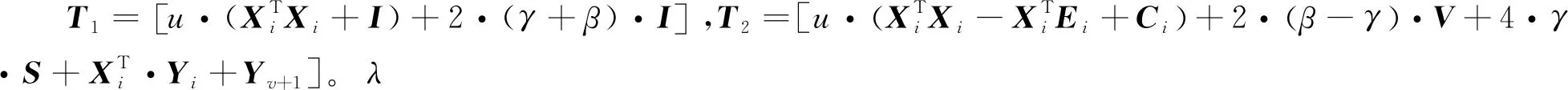
步骤6固定除V之外的所有变量，更新V，此时式(10)变为式(20):

(20)

对式(20)求导可得更新式(21):

V=(Z1)-1Z2

(21)

步骤7根据式(22)更新共识矩阵S：

(22)

步骤8根据式(23)更新参数：

Yi=Yi+u(Ei-Xi+XiVi),i=1,2,…,v,

Y=Y+u(E-D+DV),

Yv+1=Yv+1+u(Ci-Vi),i=1,2,…,v,

Y′=Y′+u(C-V),

u=min(ρu,umax)

(23)

其中，ρ是变化幅度的大小，等同于步长；umax为μ可取的最大值。

FSMC算法步骤如算法1所示：

算法1FSMC算法

输入：多视图数据X={X1,X2,…,Xv},特征直连数据D,ρ,umax,期望的误差ε。

输出：共识矩阵S。

步骤：

初始化所需的矩阵Ei,E,Ci,C,Vi,V,S,参数矩阵Yi,Y,Yv+1,Y′和参数u；

While迭代次数<最大迭代次数:

Ifi≤视图个数v:

根据式(13)更新第i个视图的误差矩阵Ei；

根据式(16)更新引入的变量Ci；

根据式(19)更新第i个视图的子空间矩阵Vi；

Endif

根据式(14)更新直连特征的误差矩阵E；

根据式(17)更新变量C；

根据式(21)更新直连特征的子空间矩阵V；

根据式(22)更新共识矩阵S；

根据式(23)更新参数Yi,Y,Yv+1,Y′和u；

If对应的误差矩阵(‖E-D+DV‖F,‖V-C‖F)<ε：/*(，)表示其中的元素分别小于ε*/

break;

else

迭代次数加1;

Endif

Endwhile

4 实验

4.1 数据集及性能指标

实验在新闻数据集BBC(BBC news)、人脸数据集ORL(ORL face)、手写数据集HW(HandWritten)和新闻组数据集NGs(NewsGroup datasets)共4个真实数据集上进行，其中BBC是包含4个视图的文本数据集，而ORL、HW和NGs都是包含多个视图的图像数据集。这4个数据集的简况如表1所示。

Table 1 Datasets

本文选择了ACC、NMI和F-score来评估提出算法的聚类性能。3个指标计算公式分别如式(24)～式(26)所示：

(24)

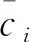
(25)

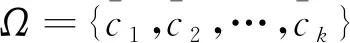
(26)

其中,Precision为精确率；Recall为召回率;τ为平衡两者权重的参数，一般情况下其值为1，表示两者重要程度一样。上述3个指标的值都在[0,1]内，越接近1表示算法性能越好。

4.2 实验结果与分析

为了评估本文提出的FSMC算法的多视图聚类性能，本文将FSMC算法与5个不同时间段提出的算法进行对比实验，这5个算法分别是谱聚类SC(Spectrual Clustering)[11](在本文中分别用单个视图聚类，即SCi表示在第i个视图下的谱聚类算法，值得注意的是在HW数据集上选择了结果较好的4个视图)、基于质心的多视图低秩稀疏子空间MLRSSC (centroid-based Multi-view Low-Rank Sparse Subspace Clustering)算法[12]、用于多视图聚类的图学习MVGL (Graph Learning for MultiView clustering) 算法[18]、基于图的多视图聚类GBS-MV (Graph-Based System for Multi-View clustering)算法[19]和多图融合的多视图子空间聚类GFSC (multi-Graph Fusion for multi-view Spectral Clustering) 算法[15]。表2～表5给出了这6种算法在4个数据集上的实验结果。

实验中每个算法运行10次，然后取平均值和标准差作为最终的性能指标值。对于权重参数，考虑到复杂性，假设其多视图数据与特征联合数据的权重占比是一样的，即暂且认为其对于最终聚类结果的影响同等重要，因此将权重参数α设为0.5，而权重参数对于聚类结果的影响可以参照图2，该图给出了当其余参数固定时，α参数对BBC数据集聚类结果的影响。

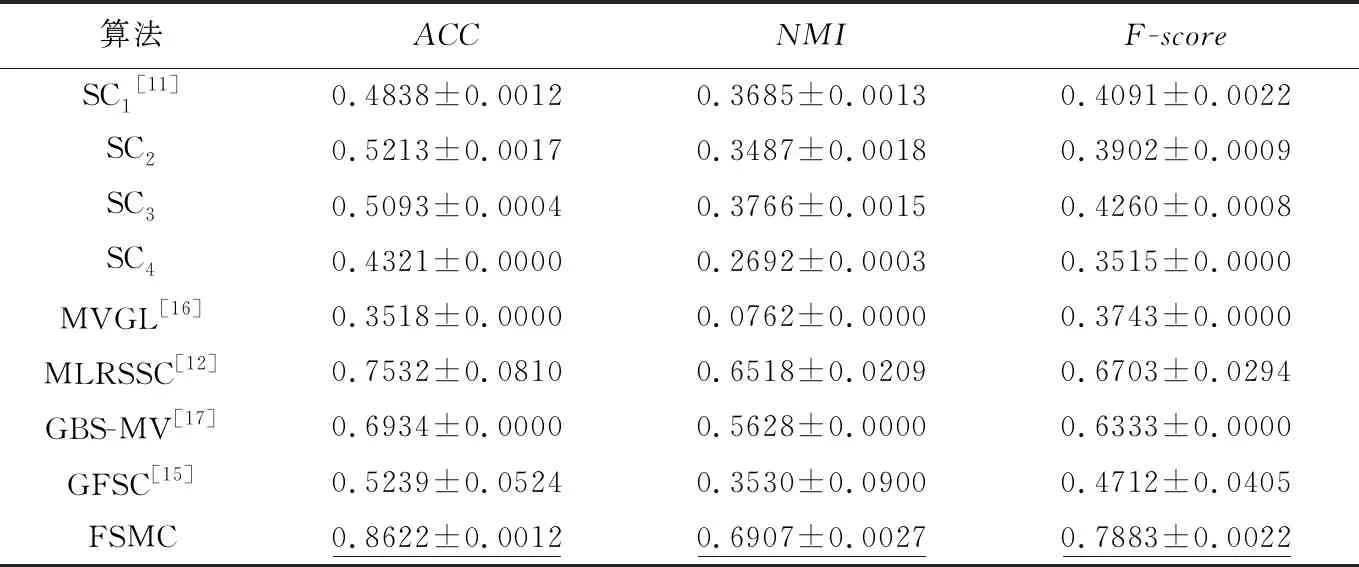
Table 2 Comparison results of different algorithms on BBC dataset

Table 3 Comparison results of different algorithms on ORL dataset

Table 4 Comparison results of different algorithms on HW dataset

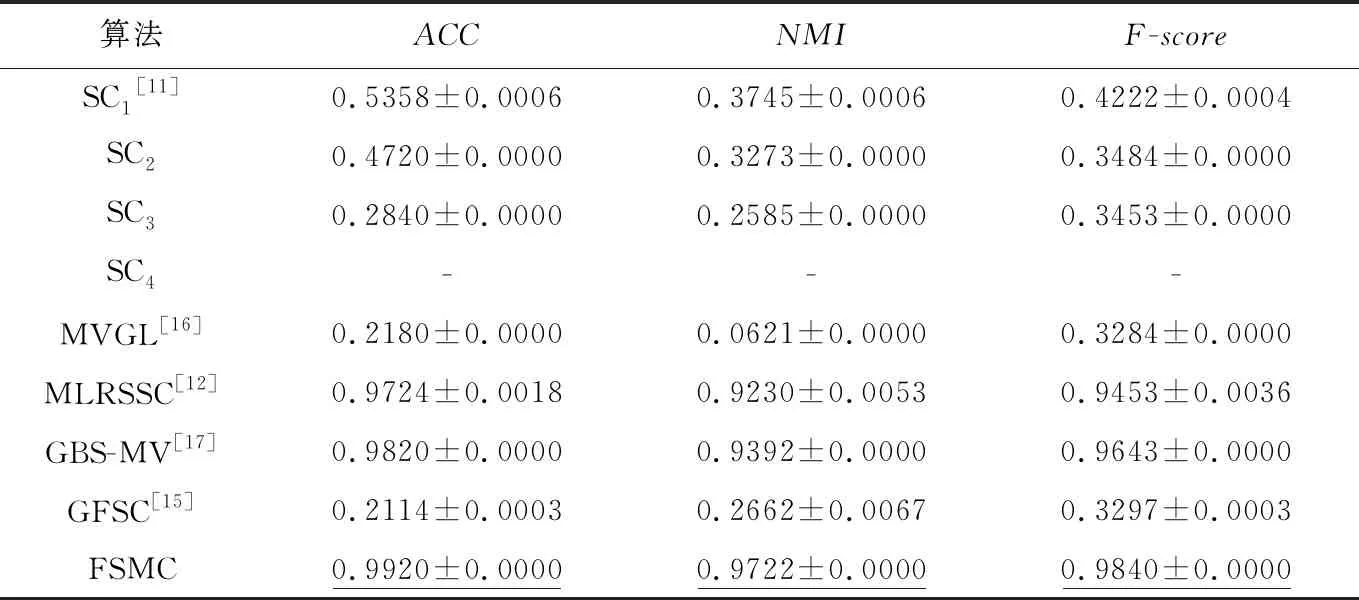
Table 5 Comparison results of different algorithms on NGs dataset

Figure 2 Effect of parameter α on BBC dataset

由表2～表5可以看出，本文提出的算法FSMC在ACC、NMI和F-score指标上都有明显的改善，也就是说FSMC能在4个数据集上实现更好的聚类结果。从表2中的数据可以看出，对于BBC文本数据集，FSMC算法在聚类指标ACC、NMI和F-score上有了显著的提高。从表2还可以看到，谱聚类作用于单个视图的性能并不好，而FSMC相比5个对比算法中最优的MLRSSC算法在ACC、NMI和F-score指标上分别提高了14.47%，5.96%和17.6%。从表3可以看出，虽然FSMC算法在ACC和F-score上相比于最优的算法有所下降，但是也明显优于其他对比算法，而且ACC相比于最优的算法(GBS-MV)也提高了1.7%。而表4的实验结果显示FSMC在ACC上优于5个对比算法，且有显著的提升，但是其余2个指标相比MVGL与GBS-MV来说是略有降低的。表5的实验结果则显示在NGs数据集上，FSMC在3个评价指标上接近1，说明聚类结果只有少量的错误，能达到一个接近完美的准确度，ACC、NMI和F-score相比于最优的对比算法GBS-MV来说分别提高了1%，3%，1.97%，明显优于最新的多视图算法GFSC。GBS-MV算法利用加权构造融合邻接矩阵得到统一的图矩阵可以有效地保持数据的流形结构，但是忽略了特征直连数据的相关信息；而GFSC算法则是在子空间表示的基础上增加图结构关系的选择，同样没有考虑到特征直连数据，因此两者在一定程度上都忽略了可用来聚类的部分信息。FSMC则是在子空间学习的基础上考虑到特征直连数据对最终结果的影响，将特征直连数据加入到多视图子空间学习的框架中，丰富了可用的聚类信息，有效地提升了聚类性能。

式(9)存在超参数，因此需要选择合适的参数来调节公式，以便得到更优的聚类结果。图3给出了参数α和β对BBC数据集的聚类结果的影响程度。由于涉及到3个超参数，因此需要固定其中一个超参数γ，然后再搜寻合适的α和β。图3给出了在γ固定为100时，不同的α和β对于ACC指标的影响。如图3所示，α=10,β=100时，对BBC数据集进行聚类得到的准确率为0.86；而在α=1,β=0.1时得到的准确率就会降低，所以选择合适的超参数也是十分重要的。图4给出了FSMC算法在BBC数据集上的迭代过程。从图4可以看出，FSMC算法在迭代了13次左右就趋于稳定，换句话说，该算法能实现快速收敛。

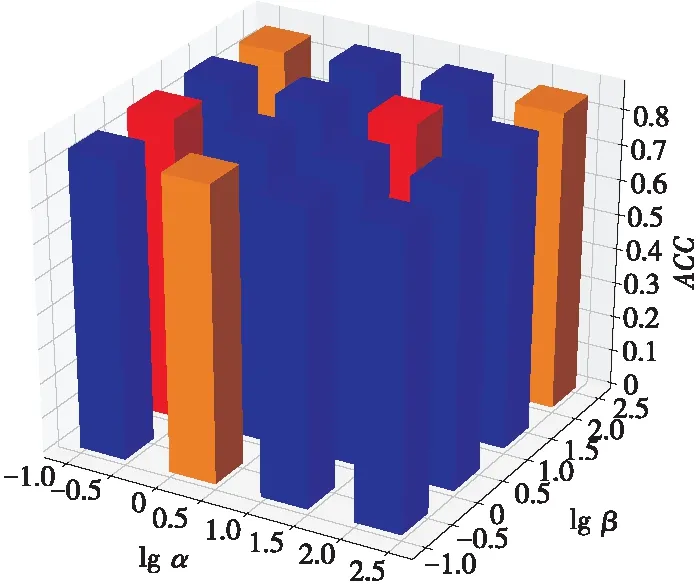
Figure 3 Impact of α and β on ACC indicator when γ=100

Figure 4 Convergence of FSMC on BBC dataset

5 结束语

本文在多视图子空间聚类算法的基础上提出了基于特征直连和重构误差的多视图聚类算法。与现有的算法不同，FSMC在原有的视图中增加了一个特别的视图数据——特征直连数据，让算法学习的信息更加丰富。同时通过重构误差矩阵使误差稳定，在保证表示矩阵结构稀疏的同时学习到特征直连视图与其余视图的差异性，最终通过共同学习得到最终的表示矩阵。本文在4个真实数据集上评估了算法的聚类效果，验证了算法的有效性。但是，FSMC算法只考虑多视图与特征直连视图之间的权重，没有考虑到多视图之间的权重，而且没有探寻特征直连数据的子空间结构，后续工作可以考虑在这2个方面改进。