多层有砟轨道结构弹性波波动行为及带隙特性

张鑫浩，赵才友，张孝娟

（1.西南交通大学 唐山研究生院, 河北 唐山063000； 2. 西南交通大学 高速铁路线路工程教育部重点实验室，成都610031； 3.西南交通大学 土木工程学院，成都610031）

交通强国，铁路先行。近二十年来，铁路轨道在我国得到了持续快速发展，运营线路、总里程以及投入总金额等均稳居世界前列。与此同时，随着中国铁路交通线网不断加密，列车速度不断提高，由之诱发的振动与噪声问题愈发严重，越来越引起人们的注意，振动和噪声已被列为七大环境公害之一[1]。轨道结构的振动与噪声辐射的本质原因可归结于结构中的弹性波波动效应[2]。已有研究表明周期结构或声子晶体具备特殊的力学特性，使得弹性波在某些频段无法传播，通常将上述频率段称之为“带隙”或“禁带”[3]。现代铁路轨道通常被设计成一些具有重复且相同的结构单元，因此可参照声子晶体或周期结构的思路进行研究。

迄今为止，针对周期结构的理论研究正在不断开展。Brilliouin对链式周期结构中弹性波的波动进行研究，为周期结构的研究建立了理论基础[4]。Mead根据波动方程研究了周期性梁、板结构的振动特性，证实了周期约束的梁、板结构中的弹性波也存在带隙特性，并提出了空间谐波法、传递矩阵法等带隙计算方法[5]。Heckl 对质量弹簧系统的不同支承方式进行讨论分析，并研究了周期性支承Timoshenko梁中纵波、扭转波、弯曲波的耦合振动特性[6]。

在对周期结构的工程实践问题的研究中，Yu等采用传递矩阵法计算了周期性输流管道中弯曲波传播特性[7]。Yu 等根据城市轨道交通噪声频谱特性，通过引入周期结构带隙理论，提出了一维气-固周期型隔声声屏障结构[8]。冯青松等通过有限元法计算了欧拉梁中温度力对带隙的影响，但模型过于单一[9]。王平、易强等计算了单层点支撑、双层点支撑轨道模型中的带隙特性，研究了扣件刚度的影响，并从功率流的角度阐释了带隙特性，但并未考虑更为复杂的轨下基础以及相应的波动模式[10-12]。此外上述研究多采用传递矩阵法（Transfer-Matrix Method简称TMM），仅能适用于一维周期结构，且对于复杂结构，传递矩阵法会出现矩阵病态甚至无法求解的问题，由此本文将声子晶体研究方法中适用性更为广泛的平面波展开法(Plane Wave Expansion 简称PWE)引入轨道周期结构的带隙计算中，以期应用于计算复杂轨道结构以及二维、三维频散曲线。总之，周期性轨道结构弹性波传播的研究取得了很大的进展，但更为细致的工作和技术革新还有待于进一步深入的研究。

1 多层有砟轨道模型与波动方程

基于平面波展开法的基本原理，将有砟轨道以离散点支撑模型进行建模，见图1，取轨枕间距l内的钢轨及其轨下各支撑部件为一基本元胞，根据Bloch 定理及Floquet 变换，求解无限周期结构的频散特性[13]。

图1 多层有砟轨道结构及基本元胞模型

在频率波数域中的钢轨位移解为：

轨枕和道床的位移解为：

建立多层有砟轨道基本元胞振动方程式（5）、式（6）、式（7），将式（1）至式（4）代入振动方程式（5）、式（6）、式（7），可得频率波数域下的频散方程式（8）、式（9）、式（10）：

其中：k是限制在一维Brillouin区的波矢，wGm是一维倒格矢G对应的傅里叶系数。kr为扣件支撑刚度，ks为轨枕支撑刚度，kb为道床支撑刚度，Ir为钢轨截面惯性矩，mr为单位长度钢轨质量，ms为轨枕质量，mb为道床参振质量，Er为钢轨弹性模量。

Gm取遍整个倒格矢，而实际计算中为所得到的该问题近似数值解，将钢轨平面波数设置为n，总倒格矢数则有m=2n+1 个，则上述方程可化简为经典平面波展开矩阵形式：

式中：P、Q均为（2m+1+2）阶方阵，α为（2m+1+2）阶列阵，从第一布里渊区选取波数k，即可得到轨道结构的能带结构。

2 频散曲线与带隙

本文钢轨平面波数取为41，既可以充分保证解的收敛，又不会使计算繁琐。多层有砟轨道结构的相关参数如表1所示。

表1 有砟轨道结构参数表

利用上述方法可以得到多层有砟轨道结构频散曲线，如图2 所示，在0～57.4 Hz、72.14 Hz～122.2 Hz、141.9 Hz～243.5 Hz、1 454 Hz～1 490 Hz 出现带隙特征，且与采用传统的传递矩阵法计算得到的带隙范围相一致。

图2 频散曲线及带隙图

3 轨道参数的带隙影响规律

多层有砟轨道结构各部件的参数直接影响带隙特征，如图3所示，随着扣件支撑刚度增加，1阶带隙带宽增大，2阶带隙带宽不变，并向高频移动，3阶、4阶带隙的带宽增大并向高频移动；随着轨枕支撑刚度增加，1 阶、2 阶带隙带宽增大，3 阶带隙带宽减小并向高频移动，4阶带隙保持不变；随着道床支撑刚度增加，1 阶带隙截止频率增大，2 阶带隙向高频移动，但带宽不变，3阶带隙起始频率增大，4阶带隙保持不变；随着元胞尺寸增大，1、2、3阶带隙带宽均逐渐减小，而4阶带隙带宽不变，并向低频移动。根据上述规律，可以通过调控扣件、轨枕、道床的支撑刚度以及元胞间距等参数，实现对轨道结构弹性波传播的控制。

图3 轨道结构参数对带隙的影响

4 带隙机理及带隙边界模式

现有研究表明，局域共振模型中依然存在Bragg带隙，当周期结构的基本元胞长度为a时，Bragg 带隙表征为元胞尺寸为半波长的整数倍，即：

经验算可知，第4 阶带隙（1 454 Hz～1 490 Hz）为Bragg 带隙，且符合上述公式计算结果。在多层有砟轨道结构中，还存在局域共振带隙，采用集中质量模型来描述带隙的边界模式。令：

其中带隙起始频率模式满足式(15)：

考虑到M＞＞m，即要求解：

且

带隙截止频率模式满足公式：

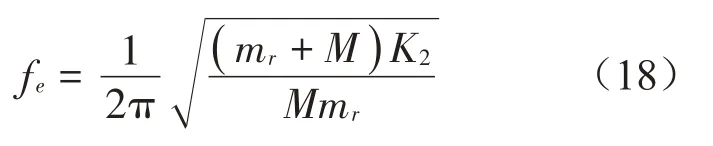
考虑到M＞＞m，即要求解：

且

其中，起始频率3 个正解对应的振动模式如图4 所示，截止频率3 个正解对应的振动模式如图5 所示，其中实线代表初始位置，虚线代表变形后位置。

图4 带隙起始频率振动模式

图5 带隙截止频率振动模式

5 有限周期结构振动传递系数

为验证多层有砟轨道结构的带隙特性，分别建立5 周期与10 周期有限周期结构模型，计算单位简谐荷载下不同位置处的钢轨响应。激励点位置响应为u0，第n跨处的钢轨响应点响应为un，钢轨振动传递系数为：

通过上述方法得到振动传递曲线如图6 所示，可以看出传递曲线在（0～130 Hz）频段内传递率均小于0，且最大衰减率达52 dB，弹性波无法传递，即存在带隙特性。同理，在（72 Hz，122.4 Hz）、（142 Hz，245 Hz）存在明显带隙，且最大衰减率分别达到150 dB 和125 dB。而对于频散曲线中的第四阶带隙频段，由于其带宽窄且衰减率较低，故传递曲线中的带隙特征并不明显。除上述频段外，在其余频率范围内传递系数均大于0，振动无衰减，即为通带。根据平面波展开法计算所得的带隙特征，与根据振动传递规律所得结果完全吻合。因此，验证了带隙的存在以及计算的正确性。

图6 有限周期振动传递系数

6 通带与带隙范围内弹性波传播特性

为进一步分析多层有砟轨道结构中弹性波传播特性以及带隙对钢轨及环境振动的影响，建立20个有限周期的元胞结构，在元胞左端位置处施加单位简谐荷载，分别提取位于带隙范围内的60 Hz、90 Hz、200 Hz 以及位于通带范围内的70 Hz、150 Hz 、2 000 Hz的钢轨及道床位移分布。

如图7至图12所示，对于带隙范围内的频率，钢轨及道床位移会沿着弹性波的波动方向快速衰减，表现出带隙特性。此外，不同带隙范围内，衰减速度各不相同：60 Hz 位于第1 阶带隙内，弹性波传递至第13个元胞时，完全衰减；90 Hz位于第2阶带隙内，弹性波传递至第6个元胞时，完全衰减；200 Hz位于第3阶带隙内，弹性波传递至第10个元胞时，达到完全衰减。这符合上文中所计算的振动传递系数的大小关系。对于通带范围内的频率，钢轨及道床位移沿着弹性波的波动方向无明显变化或衰减，即表现出通带特性。

图7 60 Hz（1阶带隙内）钢轨及道床位移分布

图8 70 Hz（通带内）钢轨及道床位移分布

图9 90 Hz（2阶带隙内）钢轨及道床位移分布

图10 150 Hz（通带内）钢轨及道床位移分布

图11 200 Hz（3阶带隙内）钢轨及道床位移分布

图12 2 000 Hz（通带内）钢轨及道床位移分布

由此进一步证明有砟轨道结构的带隙特性，以及带隙的出现可有效抑制弹性波在环境中的传播扩散。这为抑制轨道结构中环境振动、减少噪声污染提供了新的思路和理论支撑。

7 结语

（1）本文基于平面波展开法，建立多层有砟轨道结构基本元胞波动方程，得出无限周期结构的各阶带隙为：0～57.4 Hz、72.14 Hz～122.2 Hz、141.9 Hz～243.5 Hz、1 454 Hz～1 490 Hz。

（2）多层有砟轨道结构中存在局域共振带隙和Bragg 带隙，局域共振带隙主要受到扣件刚度、轨枕刚度、道床刚度等轨下支撑的影响；Bragg 带隙主要受到扣件刚度及元胞长度的影响。垂向弯曲波局域共振带隙的产生机理及振动模式可用弹簧振子模型进行描述，并分别给出了带隙边界解的方程；Bragg带隙则由Bragg散射机理控制。

（3）求解有限周期数的多层有砟轨道结构振动传递系数，得到在各阶带隙范围内弹性波沿轨道方向的传播明显衰减，即dB值小于0，从而验证了带隙的存在及计算的正确性。

（4）对于带隙范围内的频率，钢轨及道床位移会沿着弹性波的波动方向快速衰减，表现出带隙特性，此外衰减速度与振动传递系数大小相符；而对于通带范围内的频率，钢轨及道床位移沿着弹性波的波动方向无明显变化或衰减，即表现出通带特性。由此表明了带隙对钢轨及环境振动具有抑制作用。