大潜深耐压球壳结构的声振耦合特性研究

李 凯，俞孟萨

（中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

耐压壳体是水下载人平台的核心结构，常见形式主要有圆柱壳、球壳、椭球壳以及它们的组合结构，对于工作深度超过1000 m 的大深度载人潜水器，则绝大多数采用球壳结构[1]。大潜深球壳结构具有壳体壁厚大的几何特征和静水外压高的载荷特点，如果仍然采用经典薄壳理论模型来计算评估球壳的振动声辐射性能，则可能产生较大的偏差，同时，在高静压环境下，壳体内部形成的初始应力场也会显著改变壳体的结构刚度与动力学特性，进而影响球壳的耦合振动与水下声辐射。因此，有必要针对上述问题开展深入研究，考查分析厚壁几何特征及静水压力载荷等因素对大潜深耐压球壳声振耦合特性的影响规律和影响范围。

球壳在流体介质中的声振耦合问题很早就受到了学者们的关注[2-3]：Peng[4]讨论了轴对称环形激励力的相关性对球壳声辐射的影响；陈军明[5]建立了水中加肋弹性薄球壳的声振耦合系统运动方程；Huang[6]和Zou[7]基于波叠加法提出了一种解析-数值混合方法，分别研究了单层球壳和充水双层球壳在有限水深海洋环境中的耦合振动和声辐射特性以及相应的声传播问题；Gaunaurd[8]研究了球壳内部双层质量块-弹簧系统对球壳声散射的影响；Scandrett[9]探讨了声学隐身层对球壳流固耦合特性和反向声散射特征的影响。上述文献大多采用了基于经典薄壳理论的球壳动力学模型。针对水下航行体中常见的圆柱壳结构，已有不少文献[10-13]报道了静水压力载荷对壳体耦合振动和水下声辐射性能的影响研究，但对于球壳结构，还少有文献涉及这个问题，研究的重点主要集中在内压作用对球壳振动特性的影响[14-16]。

本文针对大潜深耐压球壳结构，计入剪切变形和转动惯量的影响，推导考虑初始应力效应的厚壳结构动力学模型，再结合球面声波辐射理论，建立计及静水压力作用的厚球壳声振耦合模型，针对机械点力激励，采用模态展开法，计算分析厚壁几何特征和静水压力载荷对不同厚径比球壳耦合振动与水下声辐射特征的影响，并深入探讨上述两种因素不同影响的形成机理。

1 考虑初始应力效应的厚壳动力学模型

在壳体振动问题中，除了动态激励载荷引起的结构动应力外，壳体结构还可能预先或同时受到静载荷的作用，形成所谓的初始应力场或预应力场。从能量角度看，初始应力场对壳体振动的影响主要是给壳体总应变能带来了一个附加项。该附加项是初始应力在抵抗振动变形过程中累积的能量，由于初始应力与静载荷的静力平衡关系，附加应变能中的一部分将与静载荷做功引起的外力势能相抵消，余下部分便是初始应力场对振动位移的耦合项，代表初始应力对壳体振动的影响。

壳体内任意一点的应变-位移关系如下：

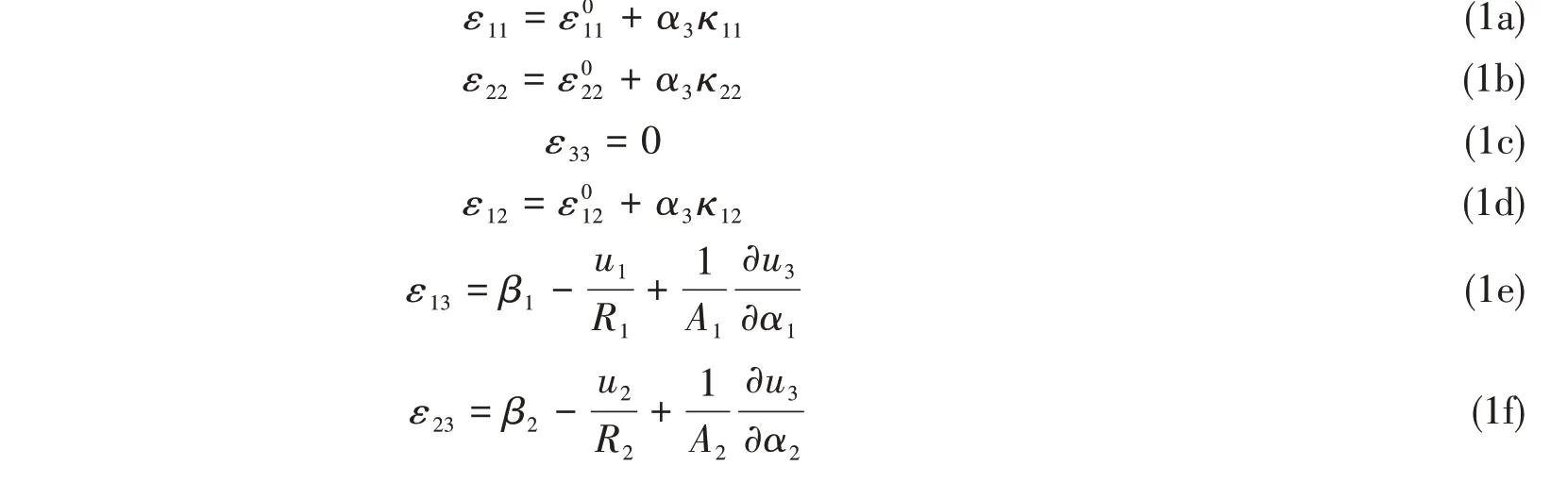
式中：α1、α2和α3分别表示正交曲线坐标系三个方向的坐标值，其中α3表示壳体厚度方向；R1和R2表示壳体中面曲率半径；A1和A2表示曲面拉梅参数；u1、u2和u3表示中面一点的平动位移；β1和β2表示中面一点的转动位移；ε、ε和ε代表中面薄膜应变；κ11、κ12和κ22代表中面弯曲/扭转应变。

与薄壳理论相比，在计入剪切变形和转动惯量后，不再满足横向剪应变ε13和ε23为0 的假设，同时，还引入了两个独立的中面角变形分量β1和β2。此外，初始应力的量值通常远大于动应力，因此需在初始应力部分的应变能计算中引入高阶形式的壳体应变-位移关系[17]，在ε、ε和ε表达式中各增加一个高阶项

应用Hamilton 变分原理，容易得到壳体的运动控制方程，方程可分解为独立的两个部分：一是与初始静载荷相关，表征壳体初始平衡状态的静力部分；二是与动载荷相关，反映壳体振动状态的动力部分，其中的动力部分即为考虑初始应力效应的厚壳振动方程，具体形式为

式中：N11、N22、N12、N21、M11、M22、M12、M21、Q13和Q23表示由动载荷引起的壳体中面单位长度的内力和内力矩；N、N、N和N表示由初始静载荷引起的壳体中面单位长度的内力；q1、q2和q3表示三个方向的动态作用力。

在考虑剪切变形和转动惯量后，式（2d）和式（2e）右端各增加了一个惯性项，方程由壳体转动方向的静力平衡方程转变为动力平衡方程。在引入初始应力场后，式（2c）)左端第4～7 项增加了4 个与静载荷相关的耦合项。如果忽略上述几项，即可退化为经典薄壳理论的壳体振动方程。

2 计及静水压力作用的厚球壳声振耦合模型

2.1 球壳振动模型

针对半径为a，壁厚为h的完整球壳结构，采用如图1 所示的球坐标系，θ、ϕ和r分别对应第1 章中一般壳体正交曲线坐标系的1、2 和3 方向，同时，将球壳径向位移和径向表面力分别改用w和p表示，壳体曲面坐标及相应的拉梅参数如下：

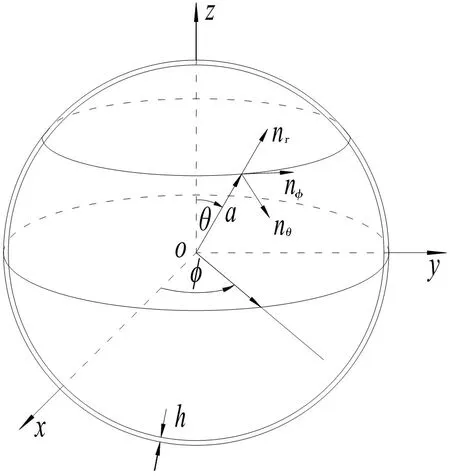
图1 球壳模型及球坐标系Fig.1 Spherical shell and spherical coordinate system

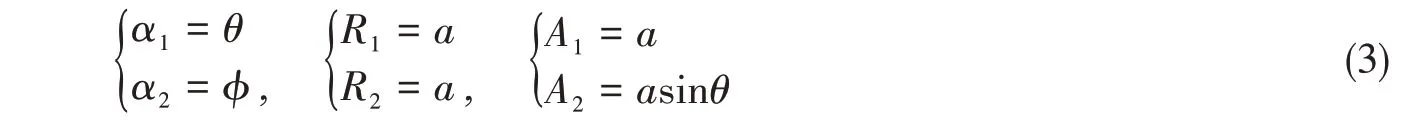
假设球壳承受均匀的静水外压为pi，由球壳的对称性易知，壳体剪应力均为0，只存在均匀的压缩膜应力，由静力平衡关系可以求出N=N= -pia/2，记作Ni，代入式（2），经整理得到中面合成力表示的球壳振动微分方程为

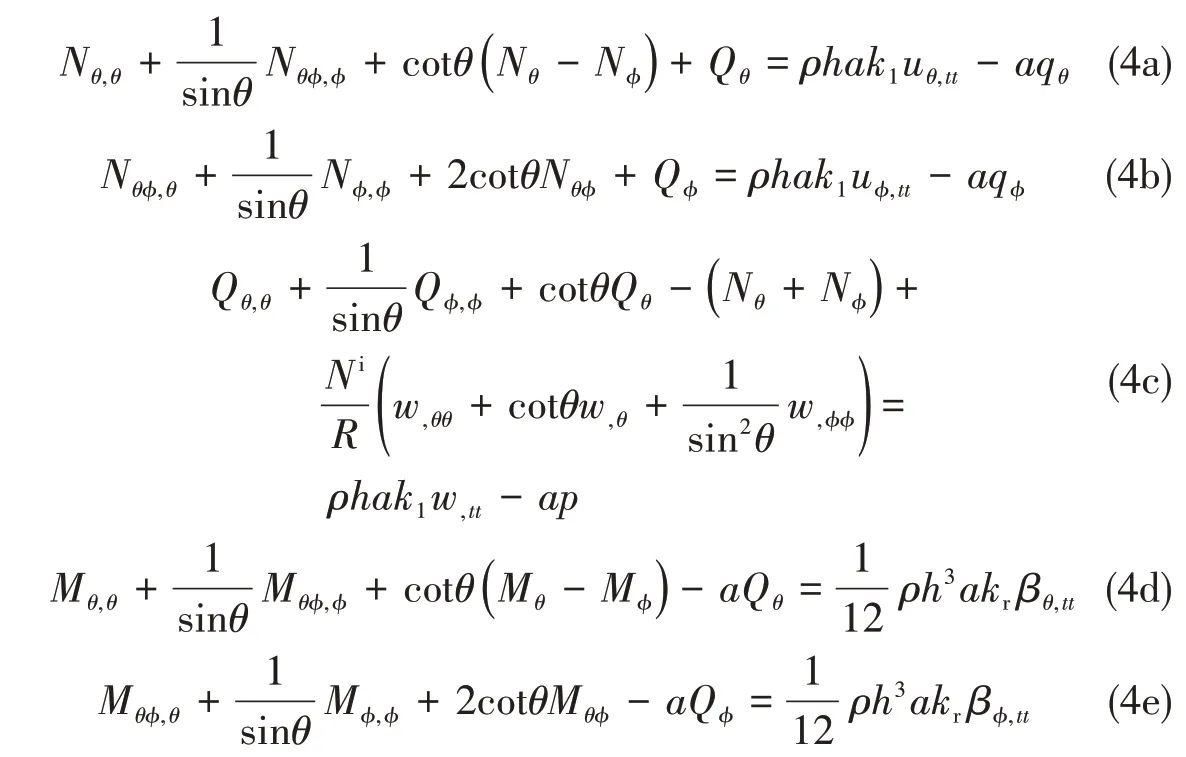
式中，

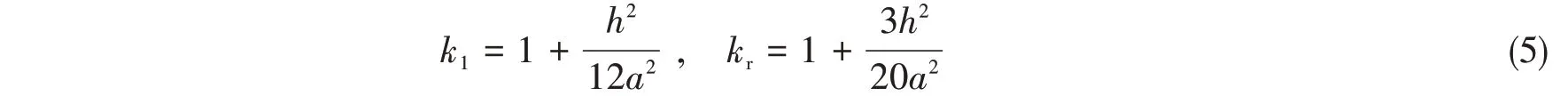
式（4c）中包含Ni的部分是计及静压作用后产生的附加项，式（2d）和式（2e）右端是考虑剪切变形和转动惯量后增加的惯性项，式（4）中的剪切内力不再由弯矩平衡方程间接取得，而是通过对横向剪应力积分获得，Qθ=Ehεθr/2ks( 1 +ν)和Qϕ=Ehεϕr/2ks( 1 +ν)，其中，ks是表征壳体截面平均剪应力的一个参数，本文取6/5。

考虑轴对称情况，舍去所有与ϕ相关的量，运用壳体应变-位移关系，将内力表示成位移的函数并代入方程组（4），化简、整理可得到一个仅包含径向位移变量w的高阶振动方程：

式中，Pn(η)表示Legendre 多项式，η= cosθ，Wn为模态展开系数。将外载荷同样用Legendre 多项式展开：

将式（7）～（8）代入式（6），对于每一个n，满足下式：

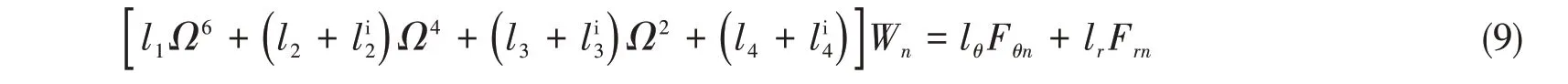
式中，Ω2=(ωa/cp)2，其余系数如下：

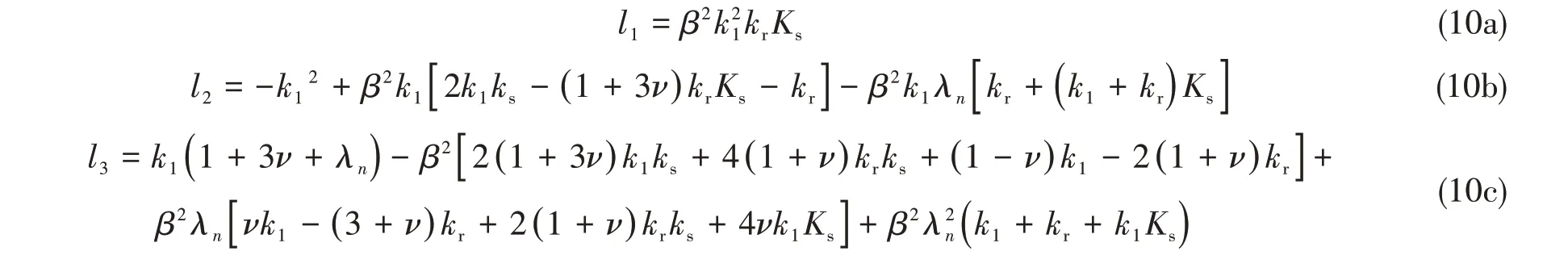
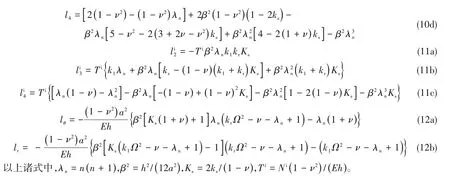
式（10）～（12）中，与kr和ks相关的项是考虑剪切变形和转动惯量后引入的附加项，与Ni相关的项是计及静压作用后引入的附加项，若取k1= 1，kr= 0，ks= 0，Ni= 0，再代入式（6）或式（9），即可退化为薄壳理论模型。

假设球壳仅在径向受到机械力激励，定义球壳模态机械阻抗为

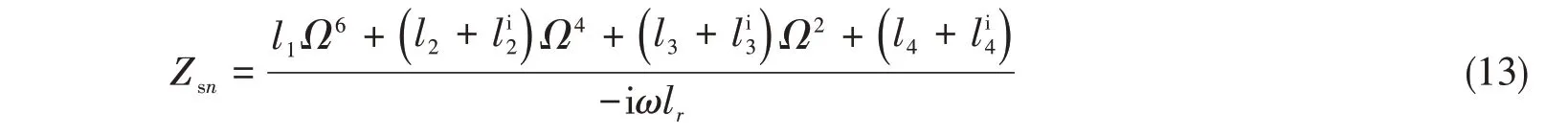
则球壳在真空中的强迫振动方程（式（9））可以改写为

对比式（13）和文献[3]中的式（7.121）可以看到：在考虑了剪切变形和转动惯量后，球壳模态机械阻抗表达式中的频率次数由4次增加到6次，意味着球壳自由振动中多出了一组与剪切相关的固有频率；同时，在计及静压作用后，模态机械阻抗中还将增加3个与静压载荷相关的附加项，这些都会对球壳的阻抗特性产生影响。

2.2 厚球壳声振耦合模型

为了计及外部声介质的耦合作用，在式（14）右端引入外声场对球壳的模态作用力iωWnZan，移项整理可得

式中，Zan为球声源模态声辐射阻抗，其表达式为[3]

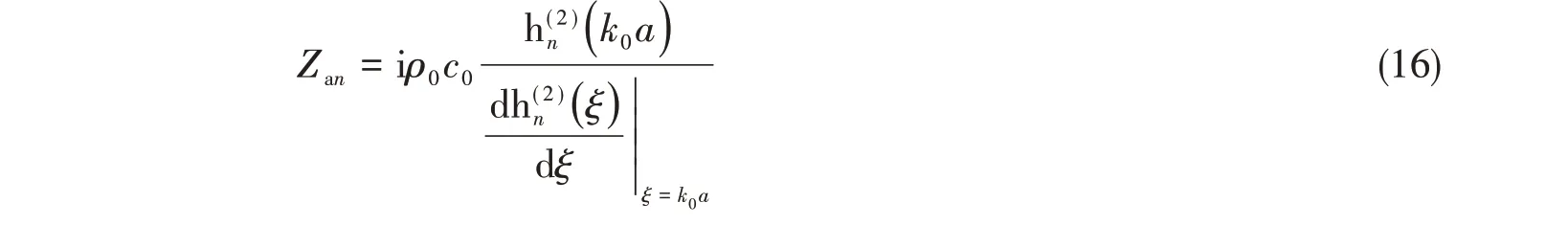
式中，ρ0和c0分别为流体密度和声速，波数k0=ω/c0，h(2)n( )是第二类球Hankel函数。

式（15）即为基于厚壳理论并计及静水压力作用的球壳耦合振动方程，求出模态位移Wn后，可采用下式计算球壳的外场辐射声压：

按照定义，球壳的辐射声功率可以由时均径向声强的球面积分得到：

球壳表面法向均方振速可由时均法向振速的球面积分得到

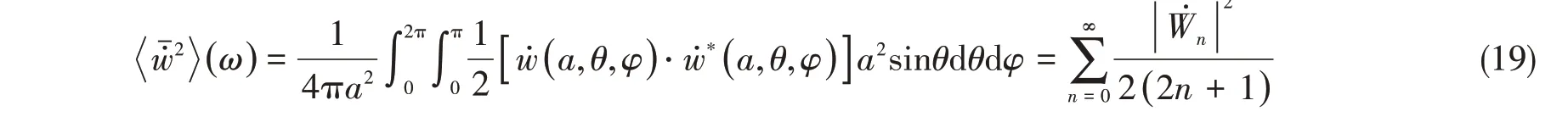
辐射声功率级和均方振速级分别定义为

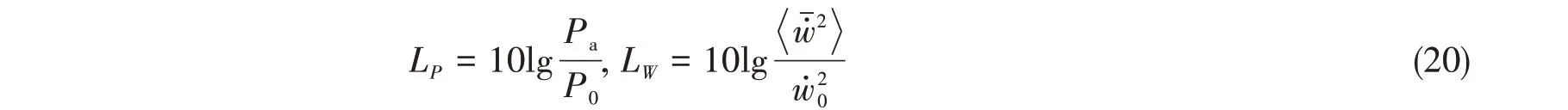
式中的基准值选取为

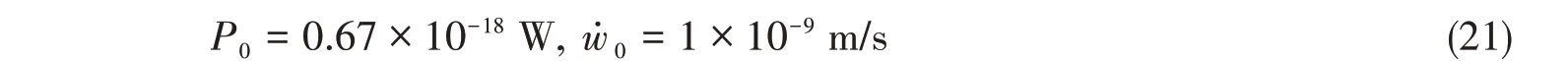
对于作用在球壳北极点，幅值为F的点激励力，其模态力可写成如下形式：

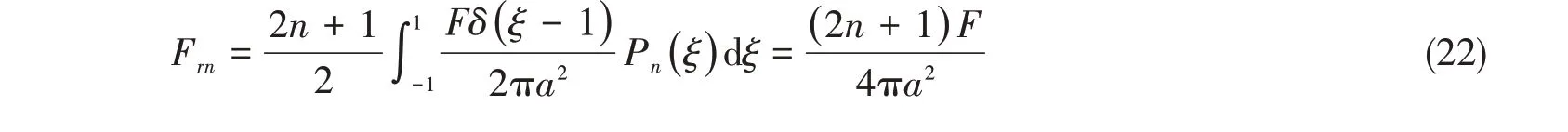
3 数值计算分析

3.1 计算模型

3.2 水中球壳的声振耦合特性

基于薄壳理论模型，计算了不同厚径比球壳在水中的耦合振动和声辐射。小壁厚球壳（h/a=0.01）在水中的振动响应远强于大壁厚球壳（h/a=0.05,0.09），且随着壁厚增加，峰值频率的间距增大，同时，中高频共振峰值逐渐消失（参见图3）。一方面，厚壁球壳的结构刚度大，模态机械阻抗也相对更大（参见图4），另一方面，由球面辐射体的模态声辐射阻曲线[3]可知，在一定频率范围内，模态声辐射阻是随频率的升高而增大的，由于厚壁球壳的固有频率更高，因而其模态声辐射阻也更大，两方面因素叠加，提升了厚壁球壳模态总阻抗幅值，从而大幅降低了厚壁球壳的耦合振动响应。另外，随着壁厚的增加和模态声辐射阻的增大，声介质对球壳振动的阻尼作用显著增强，从而抑制了中高频共振峰值的产生。

图2 耐压球壳极限强度与壁厚的关系Fig.2 Relationship between ultimate strength and thickness of a spherical shell

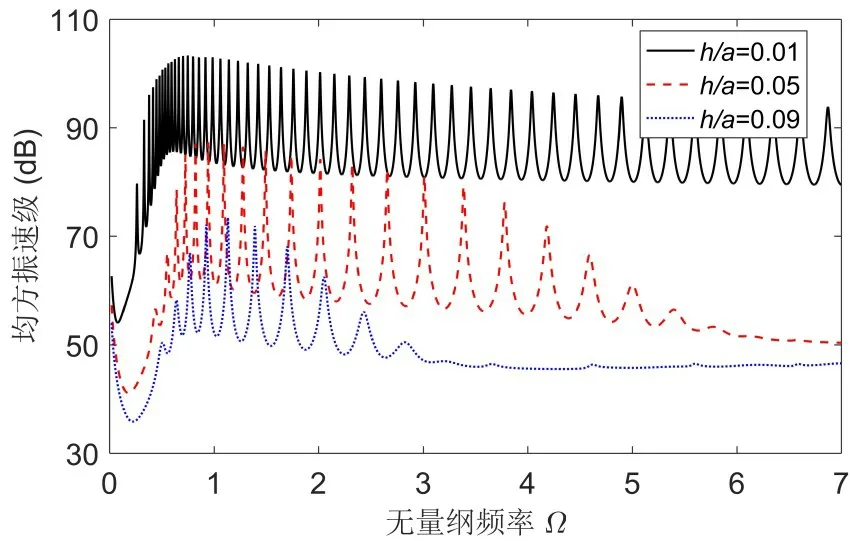
图3 不同厚径比球壳在水中的壳体耦合振动Fig.3 Coupled vibrations of submerged spherical shells with different thickness-to-radius ratios

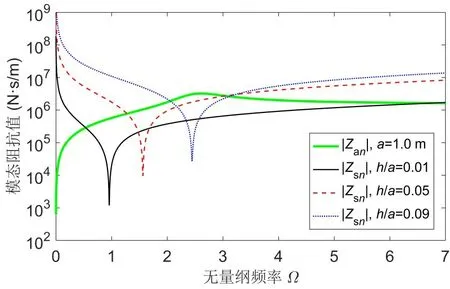
图4 不同厚径比球壳的模态机械阻抗与模态声辐射阻抗（n=9）Fig.4 Modal mechanical impedance and modal acoustic impedance of spherical shells(n=9)

由图5 可见，不同厚径比球壳水下声辐射的峰值分布特征有所不同。壁厚较小（h/a=0.01）时，峰值主要集中在低频段（Ω＜1），随着壁厚增加（h/a=0.05），中高频段也开始出现峰值，但中频段（1＜Ω＜3）的峰值要低于高频段（Ω＞3），在壁厚进一步增大后（h/a=0.09），高频段峰值逐渐消失，峰值分布范围缩小至中低频段。由式（18）可知，球壳的模态声辐射取决于模态振动响应和模态声辐射阻的乘积，只有当球壳在某阶固有频率处产生了壳体耦合共振，并且该频率点的模态声辐射阻也足够大时，才能在声辐射曲线上激发出相应的局部峰值。对比图3 和图5可见，薄壁球壳（h/a=0.01）虽然在中高频段出现了模态共振，但这些模态的声辐射阻都很小，因而未能在该频段上激发出水下声辐射峰值，而厚壁球壳（h/a=0.09）在高频段未产生壳体耦合共振，因而也没有在相应频段形成水下声辐射峰值。此外，中等壁厚球壳（h/a=0.05）在中频段的模态声辐射阻偏小，因而该频段内的峰值幅度明显小于低频段和高频段。另外，尽管厚壁球壳耦合振动的平均水平要比薄壁球壳低30 dB 以上，但是由于厚壁球壳的模态声辐射阻较高，两者在水下声辐射上的整体差距减小至10 dB 以内，表明厚壁球壳具有更高的声辐射效率。

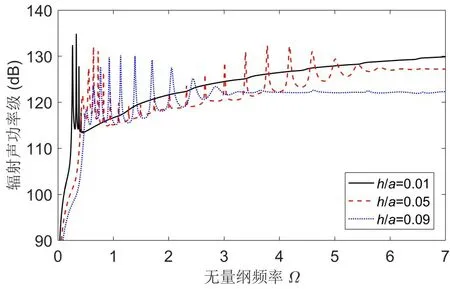
图5 不同厚径比球壳的水下声辐射Fig.5 Acoustic radiation of submerged spherical shells with different thickness-to-radius ratios

3.3 厚壁几何特征的影响

采用厚壳理论计算模型，进一步研究厚壁几何特征对水中球壳声振耦合特性的影响，并与薄壳理论模型作比较。引入剪切变形和转动惯量后，球壳的耦合共振频率将向低频方向产生一定偏移，且偏移量随频率的升高和壁厚的增加而逐步加大。在低频段（Ω＜1），不同厚径比球壳的频率偏移量均可忽略。壁厚较小（h/a=0.01）时，两种模型计算的均方振速谱级没有明显差异。当厚径比增大到0.05和0.09 时，厚壳模型计算的耦合共振峰值分别在Ω＞3 和Ω＞1 的中高频段，明显高于薄壳模型结果，最大可达18 dB左右，如图6所示。

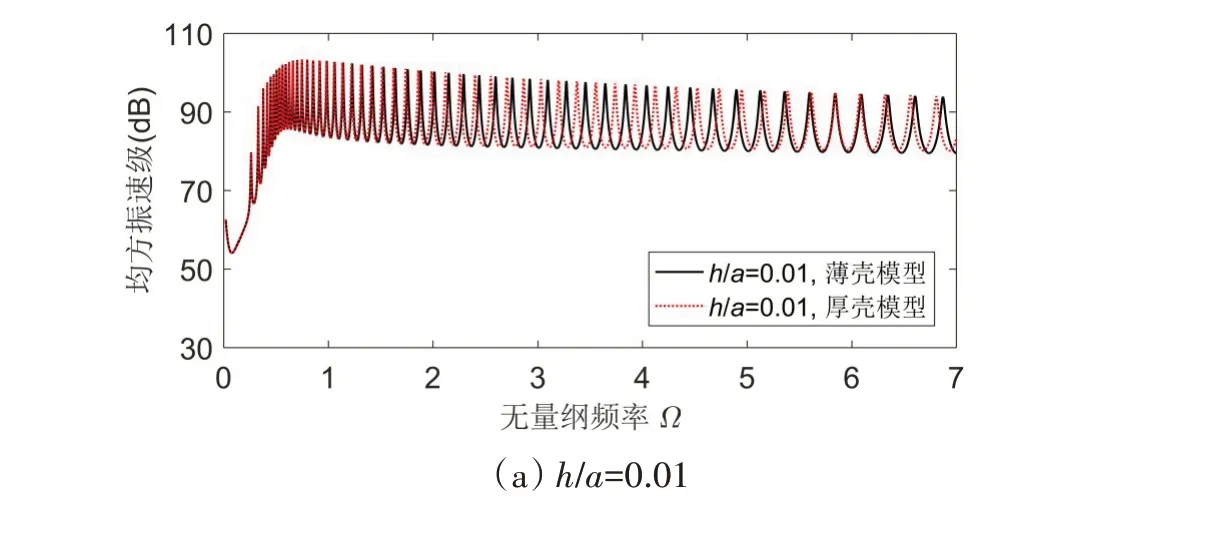
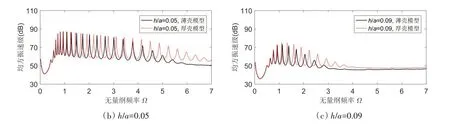
图6 剪切变形和转动惯量对水中球壳耦合振动的影响Fig.6 Influence of shear deformation and rotary inertia on coupled vibration of submerged spherical shells

图7 给出了不同厚径比球壳在薄壳理论和厚壳理论两种模型下的水下声辐射。由图可见，壁厚较小（h/a=0.01）时，两种模型的计算结果基本吻合，这是因为薄壁球壳仅在低频段存在局部声辐射峰值，而剪切变形和转动惯量对壳体低频耦合振动的影响又很小。当球壳壁厚为h/a=0.05 和h/a=0.09时，在低频段，无论是声辐射峰值频率位置还是峰值大小都没有明显变化，厚壁几何特征的影响也较小；在中高频段，球壳声辐射峰值向低频方向偏移，其中，在中等壁厚球壳（h/a=0.05）中频段，声辐射峰值出现了降低，最大降幅为4.5 dB左右，但在中等壁厚球壳高频段和厚壁球壳（h/a=0.09）中高频段，声辐射峰值则呈现出增大的趋势，最大增幅约为4.8 dB。

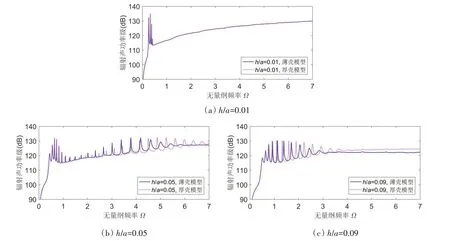
图7 剪切变形和转动惯量对球壳水下声辐射的影响Fig.7 Influence of shear deformation and rotary inertia on acoustic radiation of submerged spherical shells

3.4 静水压力载荷的影响

基于考虑初始应力效应的薄壳理论模型，计算分析静水压力载荷对水中球壳声振耦合特性的影响。图8 给出了不同极限强度球壳在计及静压作用后的壳体耦合振动，静压取值为球壳最大下潜深度时的压力值。由图可见，不同极限强度球壳耦合振动的变化趋势相近，在考虑静压作用后，壳体耦合共振频率向低频方向发生偏移，且静压载荷对小壁厚球壳固有频率的影响相对更大一些。考虑静压影响后，前3～4 阶耦合共振峰值有较明显的升高，但从其后的峰值开始直至整个中频段，共振峰值都仅有微幅降低，不过，在高频段，共振峰值又会再次出现小幅上升的现象。

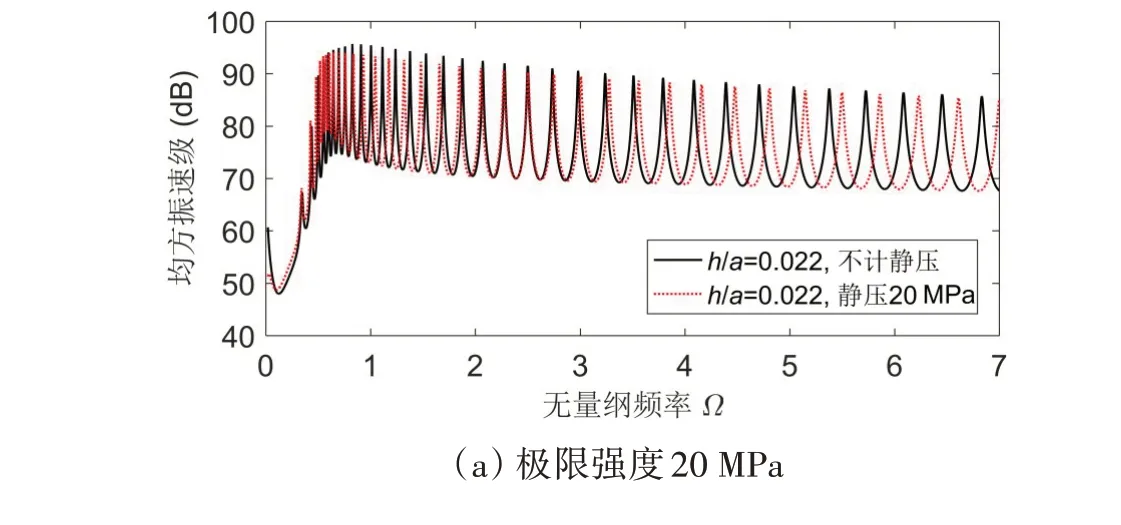
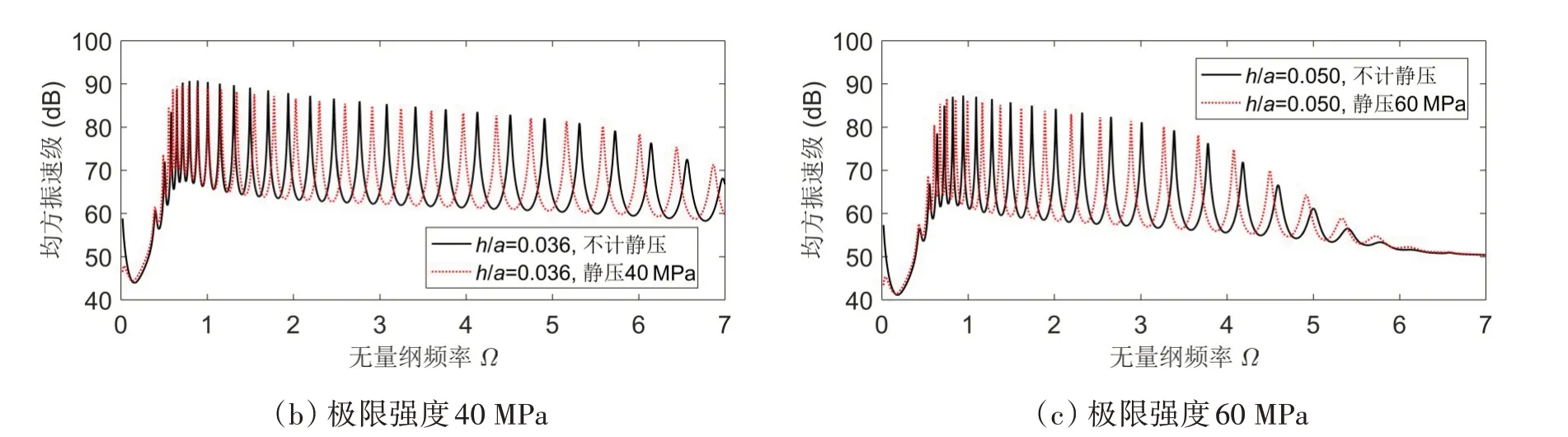
图8 不同极限强度球壳在最大静压下的壳体耦合振动Fig.8 Influence of hydrostatic pressure on coupled vibration of submerged spherical shells

图9给出了不同极限强度球壳在最大静压下的水下声辐射，考虑静压作用后，球壳水下声辐射曲线的峰值也会向低频方向产生一定的偏移，除了两个最低阶峰值处的水下声辐射会有微幅增强外，球壳在低频和中频段的多数声辐射峰值都出现了较大幅度的下降，最大超过5 dB。

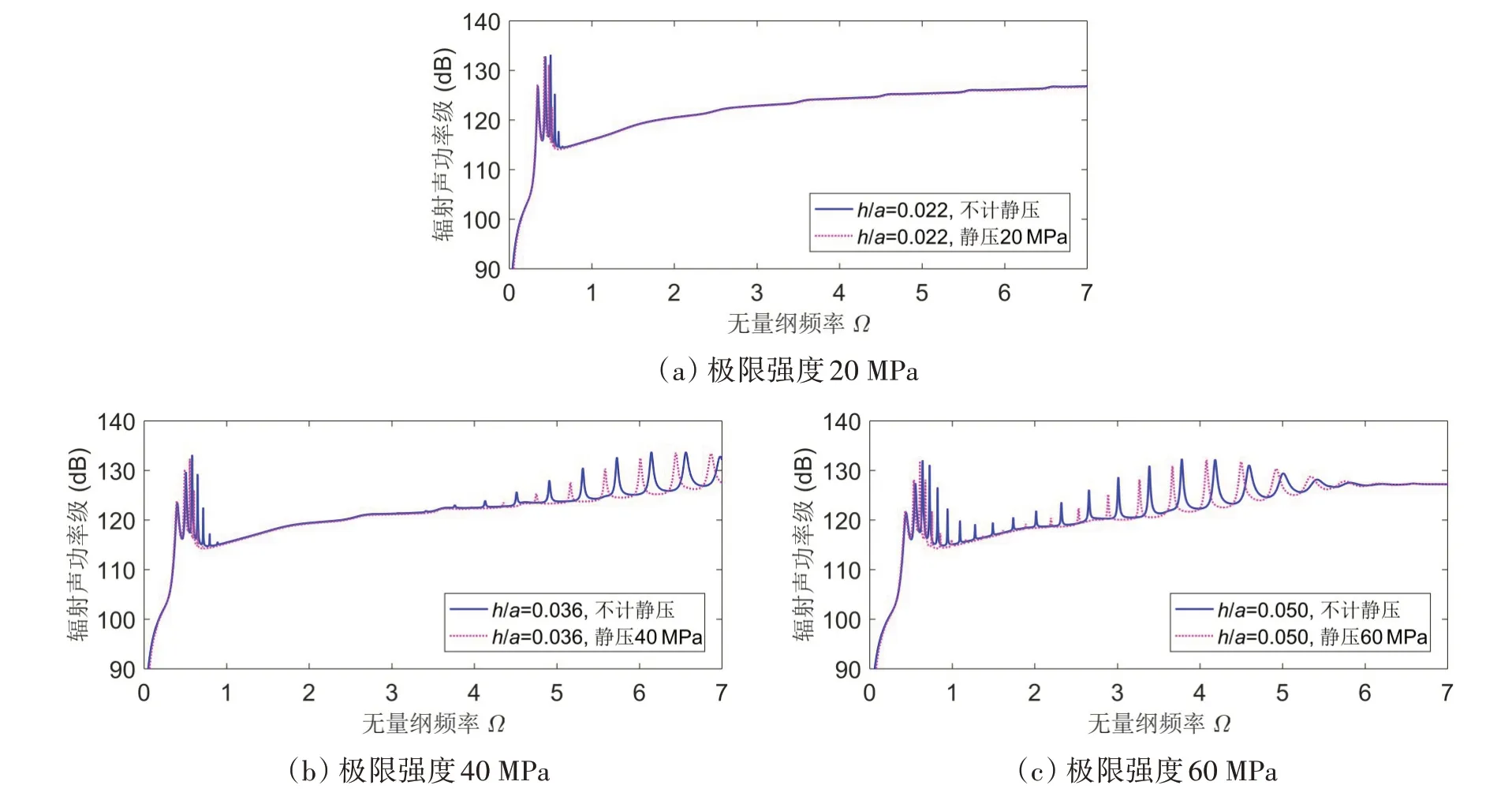
图9 不同极限强度球壳在最大静压下的水下声辐射Fig.9 Influence of hydrostatic pressures on acoustic radiations of submerged spherical shells

3.5 讨论

考虑壳体的厚壁几何特征后，附加剪切变形会降低球壳刚度，附加转动惯量会增加球壳广义质量，而计及静压载荷作用后形成的壳体压缩膜应力也会降低球壳的刚度，这些都会引起球壳固有振动频率的降低。图10给出了在厚壁几何特征和静水压力载荷等因素影响下球壳（h/a=0.05）的模态机械阻抗曲线，可以看到，上述两种因素对球壳频率特征的影响存在一定差异。在低频段，厚壳模型下球壳模态机械阻抗谷值频率的偏移很小，静压载荷的影响更大一些；随着频率升高，静压载荷对频率偏移量的影响变化不大，而厚壳模型下的频率偏移量则持续增加。不过，厚壁几何特征和静水压力载荷这两种因素对球壳模态机械阻抗幅值的影响都较小。因此，在不考虑声介质的耦合作用时，对壳体振动响应的影响也较小。

图10 厚壁几何特征和静水压力载荷对模态机械阻抗的影响Fig.10 Influence of thick wall effect and hydrostatic pressure on modal mechanical impedance of spherical shells

在考虑声介质的耦合作用后，球壳的模态总阻抗特征决定了球壳在水中的耦合振动特性。模态总阻抗由模态机械阻抗和模态声辐射阻抗两部分组成，虽然厚壁几何特征和静水压力载荷对球壳模态机械阻抗幅值的影响都不大，但随着模态振动频率的降低，各阶模态的声辐射阻抗幅值会有不同程度的减小，相应地，模态总阻抗的幅值也会出现一定的变化（见图11）。在低阶模态（n=3）处，静压影响下的模态总阻抗谷值有少许下降，这直接导致了相应频率下壳体耦合共振峰值的小幅上升（见图8（c））。不过，随着频率的增加，直到中频段，模态总阻抗幅值的变化都较小，因此，相应频段上的壳体耦合振动响应也差别不大。在高频段，模态总阻抗的谷值大幅降低，特别是厚壳模型下的阻抗计算值会降低一个量级，从而显著增强了球壳的高频耦合振动响应（见图6（b））。

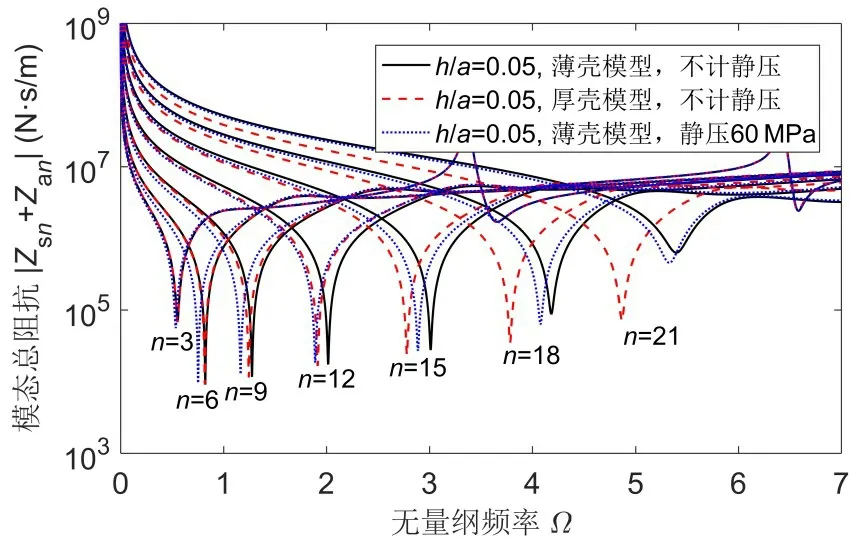
图11 厚壁几何特征和静水压力载荷对模态总阻抗的影响Fig.11 Influence of thick wall effect and hydrostatic pressure on modal total impedance of submerged spherical shells

球壳水下声辐射由壳体振动响应和模态声辐射阻综合决定。厚壁几何特征和静水压力载荷对球壳水下声辐射的影响主要取决于壳体振动响应幅值的变化及其与模态声辐射阻幅值变化的相对大小。比较图6（b）和图8（c）、图7（b）和图9（c）可见：在低频段，静水压力载荷对壳体耦合振动的影响更大，受其影响的球壳水下声辐射的变化也更大一些；在中频段，两种因素对壳体耦合振动的影响都不大，不过，受到耦合共振频率降低的影响，球壳模态声辐射阻是减小的，因此，两种情况下的水下声辐射峰值也都会出现一定程度的下降；在高频段，两种情况下的壳体耦合振动都有不同幅度的增强，但厚壁几何特征的影响显然更大，因而其对球壳高频水下声辐射的影响也更加显著。

4 结 论

本文针对机械点力激励下的大潜深耐压球壳结构，研究分析了厚壁几何特征和静水压力载荷等因素对不同厚径比球壳声振耦合特性的影响。研究结果表明：

（1）不同厚径比球壳的水下声辐射峰值分布特征差异明显，薄壁球壳峰值主要集中在低频段，厚壁球壳峰值扩展至中高频段。尽管厚壁球壳（h/a=0.09）的耦合振动响应远小于薄壁球壳（h/a=0.01）（30 dB以上），但两者水下声辐射的差距大幅缩小（10 dB以内）。

（2）厚壁几何特征引入的剪切变形和转动惯量、静水压力载荷产生的壳体压缩应力将形成附加刚度和附加质量效应，从而改变球壳的固有频率特征，降低耦合共振频率，进而影响峰值点阻抗特性以及水下声辐射幅值特征。在Ω＜1的低频段，静压载荷的影响更大，可使水下声辐射低阶峰值下降最大约5 dB（h/a=0.05）；在Ω＞1的中高频段，厚壁特征的影响更加突出，厚壳模型下的声辐射高阶峰值增加约4.8 dB（h/a=0.05）。

（3）对于h/a＜0.05 的小壁厚球壳，采用薄壳理论模型即可精确求解水下声辐射；对于h/a＞0.05 的大壁厚球壳，当Ω＞1时，应采用厚壳理论模型计算振动和声辐射，当Ω＜1时，仍然采用薄壳理论模型即可；在极限压力条件下，还应考虑静压载荷对球壳水下声辐射，尤其是低频峰值特征的影响。