基于模型试验的船舶纵倾优化技术研究

吴梓鑫，陈伟民

（上海船舶运输科学研究所；航运技术交通行业重点实验室；航运技术与安全国家重点实验室，上海 200135)

0 引 言

船舶节能减排对于保护海洋环境、提高船舶运输效率具有重要的意义[1-5]。目前常用的节能减排措施包括高效能源利用[6]、配置船舶节能附体[7-9]和优化船舶航行状态[10-13]等。其中，优化船舶航行状态是指通过调整船舶纵倾以改善船舶水动力性能。通常，船舶在实际配载中很难保证处于最佳吃水状态，尤其对于有球鼻艏的船型，球鼻艏上下区间的吃水变化会导致船体的阻力系数发生较大的差别。众多国内外学者对船舶浮态节能相关问题进行了深入研究，樊付见等[14]针对船舶压载工况建立了多目标问题优化模型，选用一艘散货船验证了图谱计算最佳纵倾工况的可行性；Emil等[15]以KCS为研究载体，设计了六种纵倾角度，系统研究了不同海况条件下纵倾对船舶运动的影响；张晶等[16]采用RANS 方程和有限体积法数值计算了一艘46 000 t 油船在设计吃水状态不同航速下不同纵倾的阻力值，分析了纵倾变化对船舶阻力的影响并拟合了相应的回归公式，为油船航行中纵倾调整研究提供了参考；Hafizul 等[17]采用模型试验和数值计算相结合的方法证明了最佳纵倾随船舶航速和吃水变化而改变，提出纵倾优化是提高船舶运营效率和降低油耗的有效方法；伍锐[18]针对某型集装箱船开展了浮态优化和球鼻艏改型技术研究，取得了明显的节能效果；Salma 等[19]采用相同网格和求解方式计算了Fn=0.2274 时KCS 不同纵倾状态的阻力，分析了纵倾对粘性阻力和兴波阻力的影响差异，指出了船舶纵倾优化对节能减排的重要意义。

近年来，随着船东对船舶规模经济效应的不断追求，超大型集装箱船订造持续兴旺，国际班轮公司加快结盟并加大订造超大型集装箱船力度。克拉克森数据显示，2018 年集装箱新船交付量共计140.85万TEU，较2017年增长18%，其中10 000 TEU以上的集装箱船运力交付占比82%。超大型集装箱船水动力性能已成为行业热点研究课题。

船模试验是评估船舶快速性能的重要手段，本文以一超大型集装箱船为载体，通过模型试验获取了船舶营运范围若干排水量和航速状态快速性数据，开发了最佳纵倾计算程序，采用双线性插值方法计算船舶在目标排水量/航速工况下的收到功率、最佳纵倾状态及对应首尾吃水，为船舶航行浮态调整提供建议。

1 数学模型

1.1 双线性插值

双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。双线性插值算法示意图如图1 所示，已知点Q11=(x1,y1)、Q12=(x1,y2)、Q21=(x2,y1)和Q22=(x2,y2)四个点，求解未知函数f在点P（x,y）的值，首先在x方向进行线性差值：

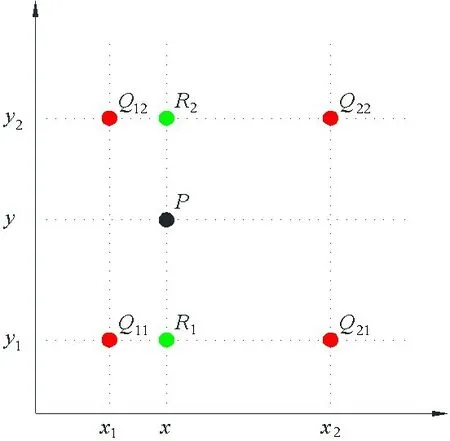
图1 双线性插值算法Fig.1 Bilinear interpolation

然后在y方向上进行线性插值：

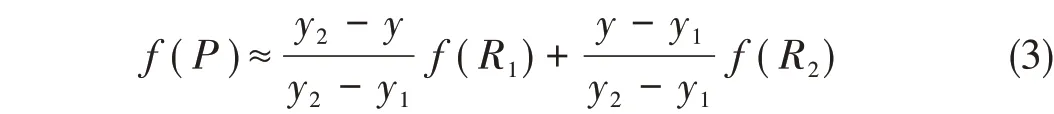
点P（x,y）即为

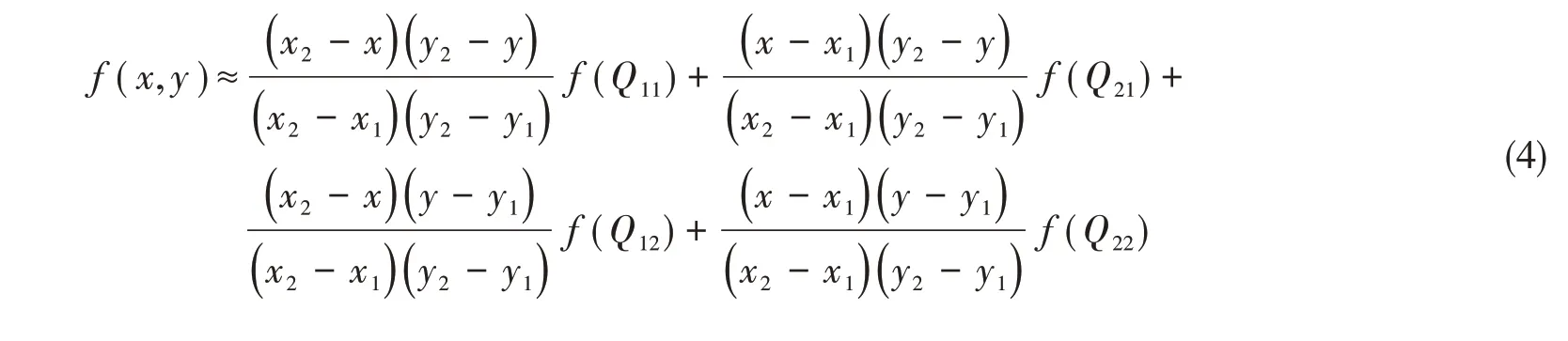
1.2 最佳浮态求解

船舶纵倾的优劣以螺旋桨收到功率作为评判依据，本文将模型试验所得收到功率Pd与试验工况排水量Δ及航速V对应整理构建不同纵倾τ状态下三维数组Qτ（Δn,Vn,Pdn），简化示意图如图2（a）所示，Q11=(Δ1,V1,Pd1)、Q12=(Δ1,V2,Pd2)、Q21=(Δ2,V1,Pd3)、Q22=(Δ2,V2,Pd4)，通过排水量Δ和航速V进行双线性插值，代入公式（4），得

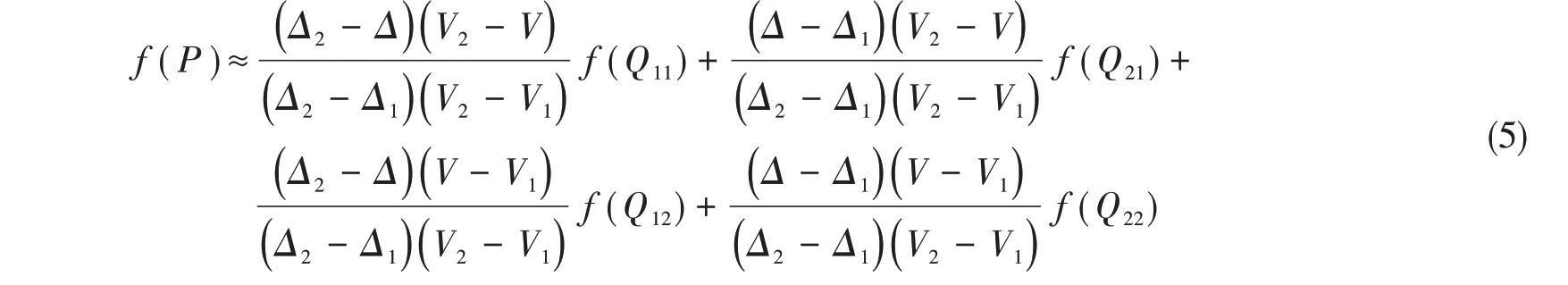
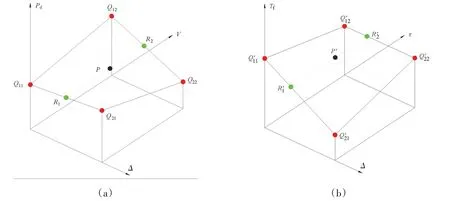
图2 三维数组求解示意图Fig.2 Solution of the 3D array

从而求得各纵倾状态下收到功率Pd_τ1，Pd_τ2，…，Pd_τn，通过建立目标排水量和航速状态下“收到功率-纵倾”函数关系（fPd_τ），可以计算得到最小收到功率Pd_min以及其对应的最佳纵倾值τ_optimized。在此同时构建了“排水量-纵倾-首吃水”三维数组Q′（Δn,τn,Tfn），简化示意图如图2（b）所示，Q=(Δ1,τ1,Tf1)、Q=(Δ1,τ2,Tf2)、Q=(Δ2,τ1,Tf3)、Q=(Δ2,τ2,Tf4)，通过排水量Δ和最佳纵倾值τ_optimized进行双线性插值，代入公式（4），得

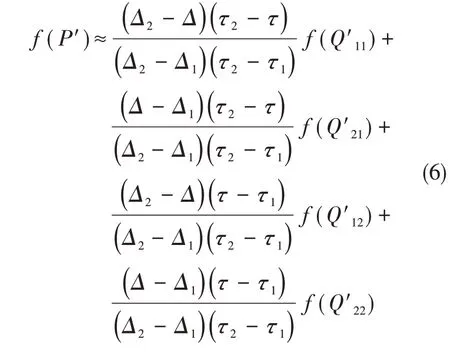
可求得对应状态的船舶首吃水Tf，结合最佳纵倾值τ_optimized，可获得相应尾吃水Ta。即通过两个三维数组、两次双线性插值，可分别得到船舶在特定“排水量-航速”条件下的最佳浮态和对应首尾吃水，具体流程如图3所示。

图3 最佳浮态求解流程图Fig.3 Flow chart of the trim optimization solution

2 模型试验

2.1 试验方法

船舶模型试验在上海船舶运输科学研究所拖曳水池进行，水池长192 m，宽10 m，水深4.2 m。阻力试验采用二因次法，摩擦阻力系数采用1957 年ITTC 公式计算求得。自航试验采用强制自航法，实船螺旋桨性能和实船性能预报采用1978年ITTC推荐的换算方法。

2.2 模型试验与工况

研究载体为一超大型集装箱船，试验采用木质船模，19 号站位和球鼻艏中间位置安装1 mm 激流丝以消除船模首部层流影响。基于超大型集装箱船营运航速及吃水统计分析[20-21]，选取100%、88%、77%、66%和55%满载五种排水量状态、18～24 kn 航速范围进行船模快速性试验，船模具体参数和试验航速如表1所示。

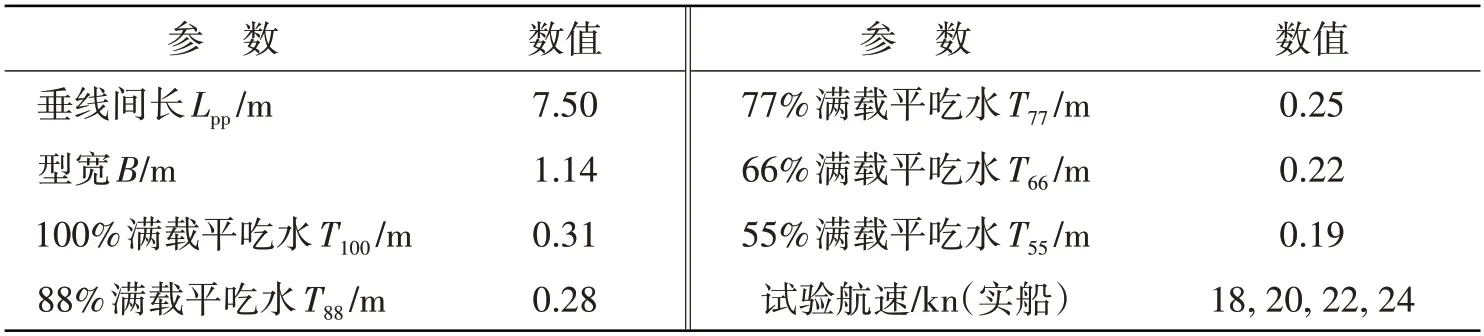
表1 模型试验船模尺度Tab.1 Main dimensions of the ship model

各排水量选取首倾2 m、平吃水、尾倾2 m 和尾倾4 m 四种纵倾工况，各纵倾状态排水量与对应平吃水排水量一致。表2为模型试验纵倾吃水工况。

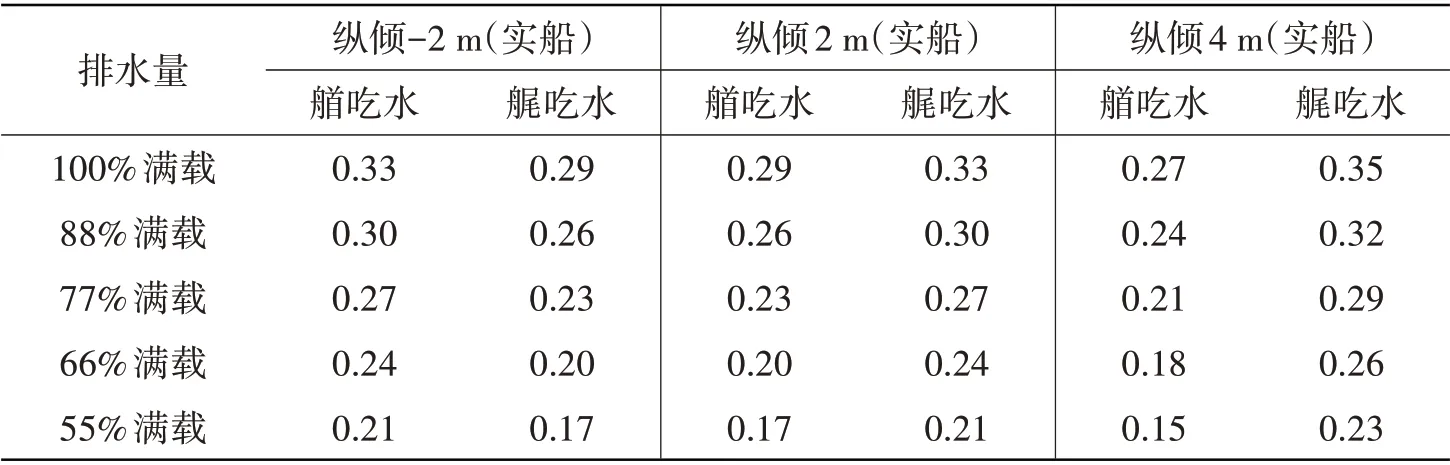
表2 船模试验纵倾吃水Tab.2 Ship draft of the model tests

图4为各排水量平吃水示意图，图5为模型试验示意图。

图4 各排水量平吃水示意图Fig.4 Draft diagram of each draft

图5 模型试验Fig.5 Model test

3 数据分析

3.1 有效功率分析

图6（a）为各排水量平吃水状态有效功率随航速的走势曲线图，图6（b）-（f）为各排水量有效功率随纵倾的变化趋势图。

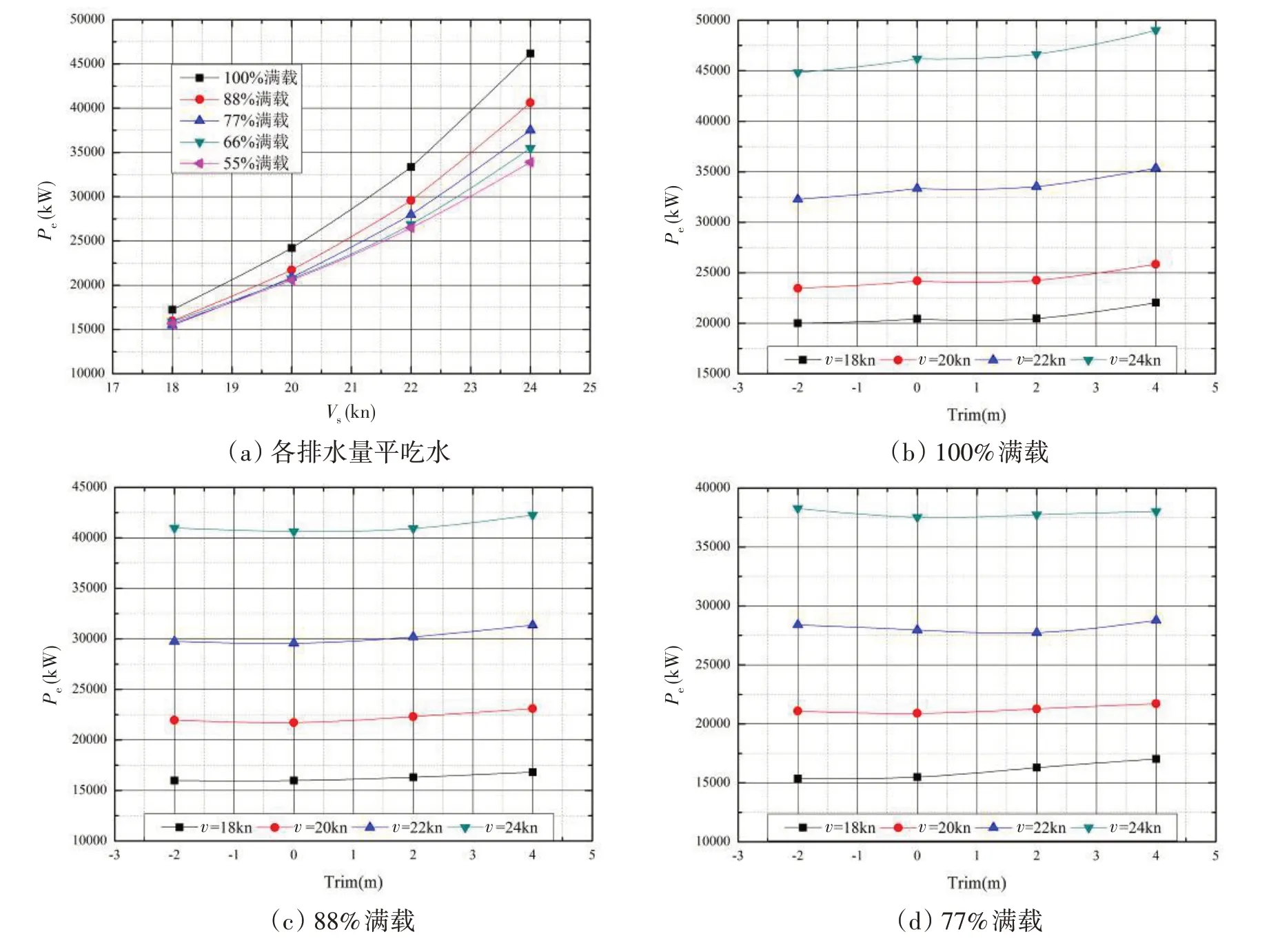
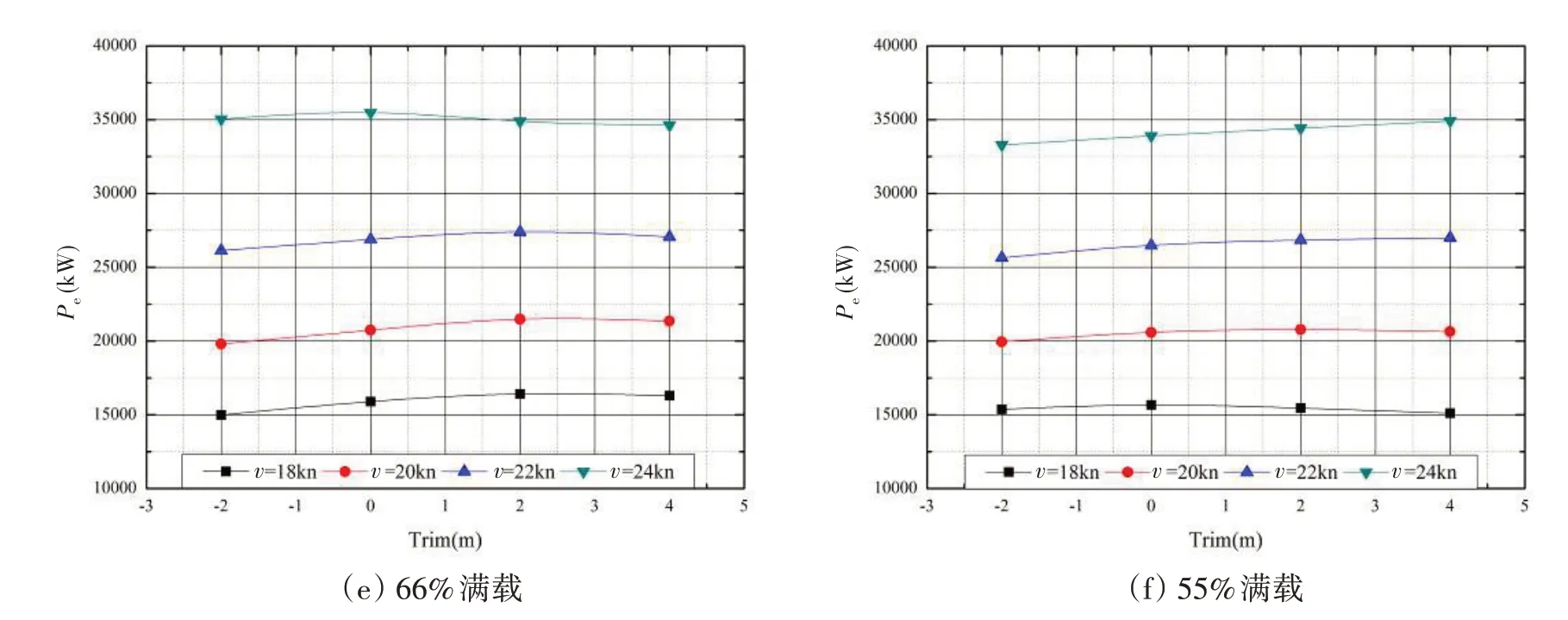
图6 有效功率Fig.6 Effective power

将各排水量平吃水状态下各速度的有效功率取为1，可得不同纵倾有效功率相对值如表3所示。

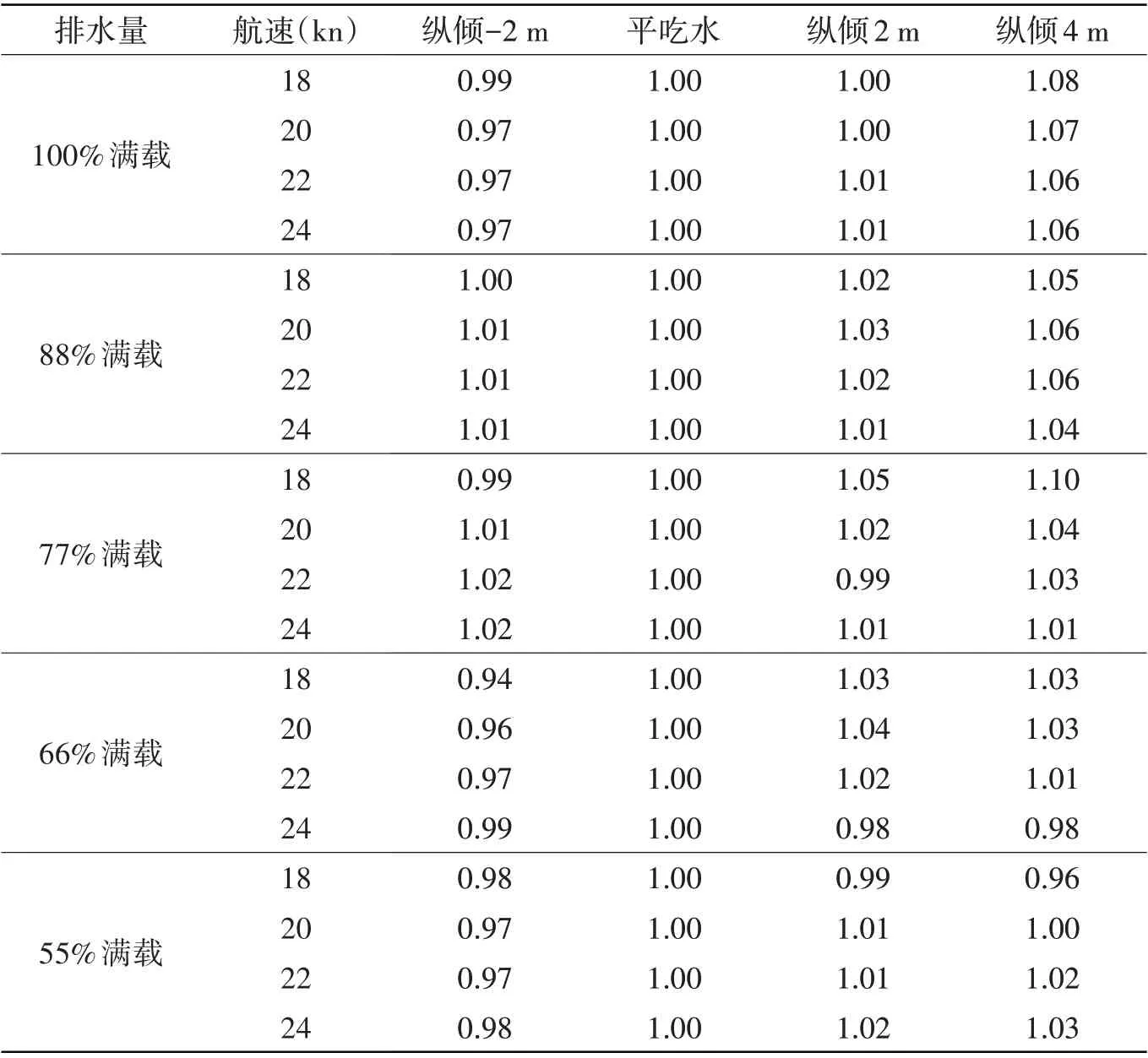
表3 各排水量不同纵倾状态有效功率相对值Tab.3 Relative value of effective power in different conditions

在同一排水量不同纵倾状态下，忽略水线长的细微变化，摩擦阻力系数可认为相等，阻力系数变化主要受剩余阻力系数影响。数据表明，同一排水量不同航速下，有效功率随纵倾的变化规律基本相同；不同排水量同一航速工况下，由于船舶航行过程中首尾线型和湿表面积等随纵倾变化不尽相同，其有效功率走势规律也有一定的差异：100%、88%和77%满载状态下，首倾2 m、尾倾2 m 和平吃水有效功率相差基本在3%以内，尾倾4 m 时，有效功率明显增加；66%和55%满载状态下，吃水在球鼻艏附近，整体上首倾2 m 时有效功率最低，尾倾状态有效功率比平吃水状态大3%以内，不同航速时变化规律略有不同。

3.2 最佳纵倾分析

最佳纵倾的选择以螺旋桨的收到功率作为依据，收到功率由有效功率和推进效率决定。图7（a）为各排水量平吃水状态推进效率，可以看出各排水量平吃水推进效率随航速走势基本相同，总体上随航速增加而降低。图7（b）-（f）为各排水量不同航速下推进效率随纵倾的变化趋势图，由于船舶在纵倾状态时，桨轴倾斜会使将盘面进流发生改变，伴流分数和推力减额相较于平吃水均发生变化，即推进效率会有一定的差异。100%和88%满载排水量时，推进效率在首倾2 m 时最大，随尾倾增大而降低；77%、66%和55%排水量状态，吃水处于球鼻艏附近，推进效率随船舶纵倾在一定区间内波动，不同排水量相同航速下推进效率随纵倾变化规律基本一致。

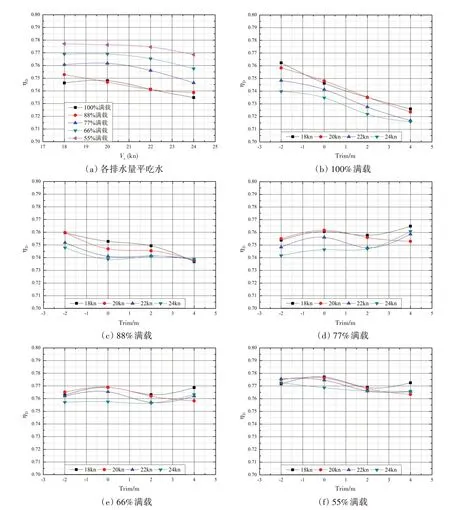
图7 推进效率Fig.7 Propulsion efficiency

将平吃水各航速下收到功率记为1，各排水量状态下不同纵倾与平吃水收到功率比值如表4 所示。分析可得，相同排水量同一航速下推进效率随纵倾变化较小，且由于阻力对船舶能耗起主要作用，因此不同排水量状态各航速下收到功率随纵倾变化与有效功率基本相同。各排水量最佳纵倾状态具体如下：100%满载排水量状态，首倾2 m 时阻力最小，推进效率最高，收到功率最低，能耗最少；88%满载排水量状态，首倾2 m 时阻力略大于平吃水，推进效率高于平吃水，收到功率与平吃水相当，尾倾状态能耗较高；77%满载排水量状态，平吃水时有效功率最低，且推进效率较高，能耗低于首尾倾状态；66%和55%排水量状态，首倾2 m 时阻力最小，推进效率在各纵倾工况差距较小，因此首倾2 m收到功率最低，在该纵倾状态下航行能耗最少。

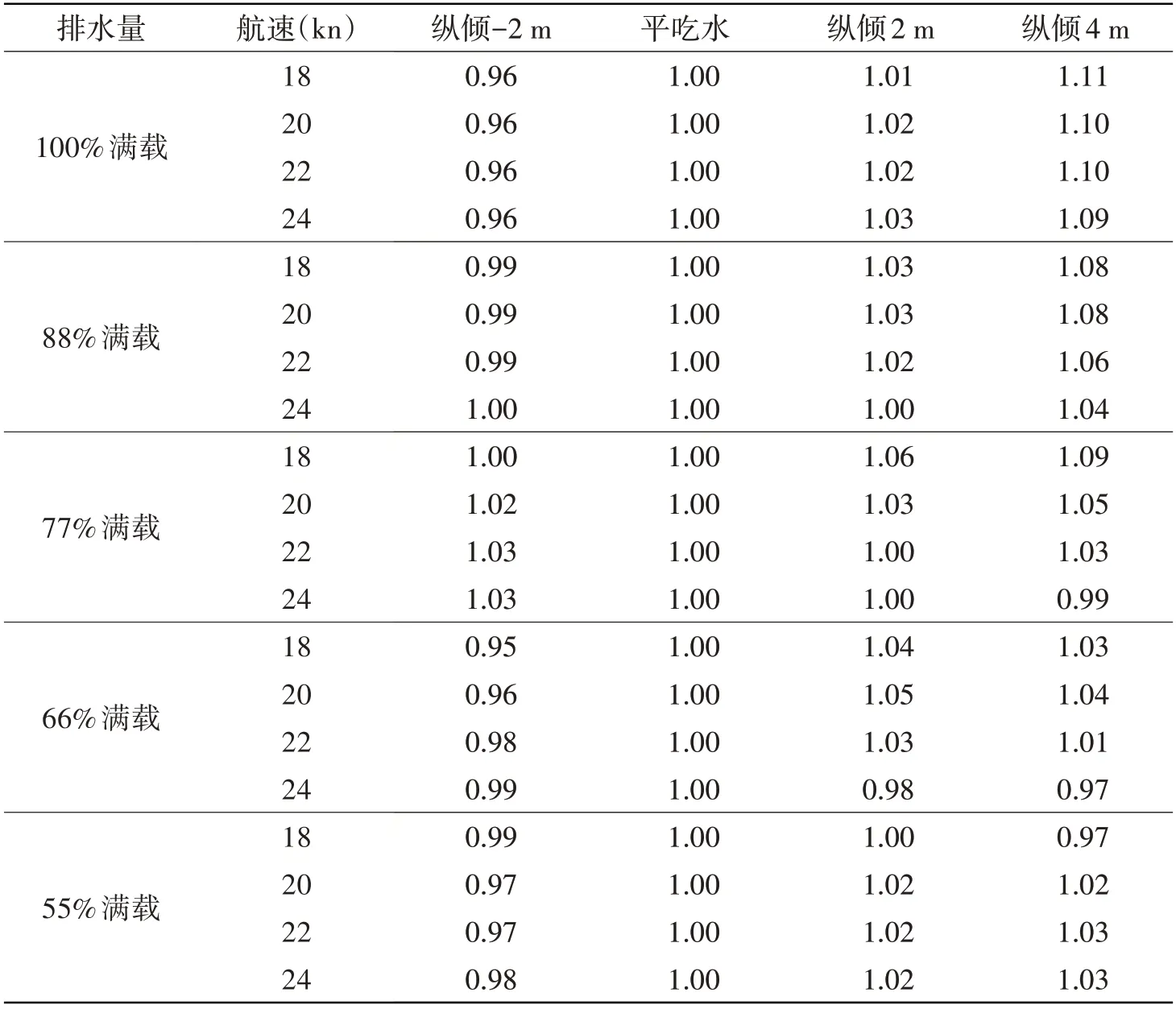
表4 各排水量不同纵倾状态收到功率相对值Tab.4 Relative value of delivered power in different conditions

4 最佳纵倾计算软件开发

基于船舶参数和试验所得快速性数据，构建了“排水量-纵倾-航速-收到功率”数据图谱，并编制开发了最佳纵倾计算软件，通过两次双线性插值计算，可迅速准确地分别获得该船在某一“船舶排水量”和“航速”工况下最佳纵倾状态及对应的首尾吃水，采用“排水量-纵倾-收到功率”三维坐标和“纵倾-收到功率”二维坐标在运行界面进行可视化展示。

选用77%满载排水量、22 kn航速工况进行程序可行性和精度验证，根据表4，该工况下纵倾-2 m、平吃水、纵倾2 m 和纵倾4 m 的收到功率相对值分别为1.03、1.00、1.00和1.03，可推断最佳纵倾应在首倾1 m 附近。图8 为软件计算示意图，计算结果表明，在该排水量/航速工况下，最佳浮态为船舶首倾0.76 m，与“最佳纵倾应在首倾1 m附近”的推断吻合。

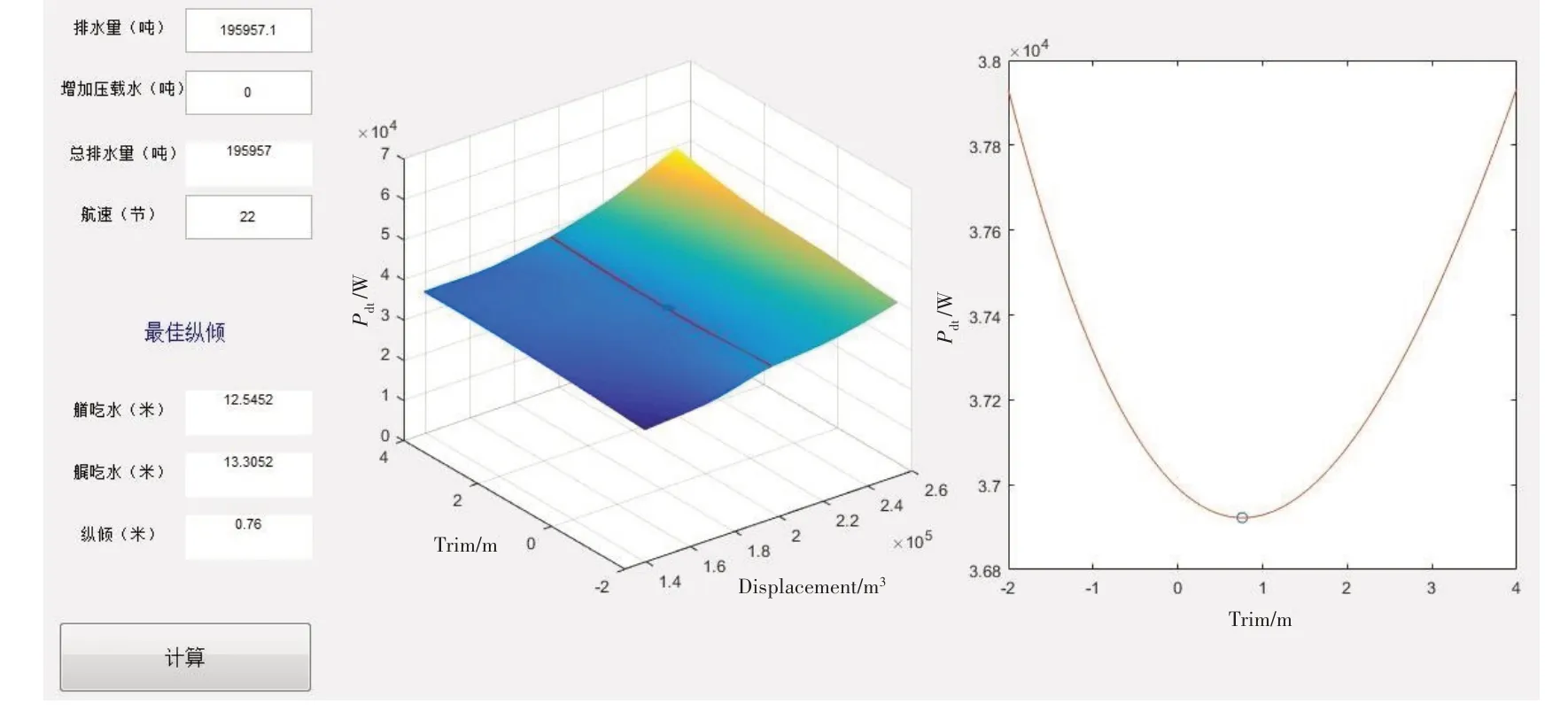
图8 最佳纵倾计算软件示意图Fig.8 Schematic diagram of trim optimization software

该浮态节能计算软件融入了船舶能效管理理念，数据基础真实可信，实用操作简单便捷，结果展示清晰明了，可通过输入排水量和航速，快速获得船舶最佳纵倾状态和其对应的首尾吃水，进而指导船舶配载调整，使船舶航行过程中减少燃油消耗，降低航运公司运营成本，减轻海洋环境污染。

5 结 论

船舶航行节能减排事关航运公司运营成本和海洋生态环境，浮态节能技术成本低廉，实际可操作性较强。本文以一超大型集装箱船为研究对象，采取模型试验手段获取了其营运范围快速性能数据，将各排水量纵倾状态下有效功率和收到功率结果与平吃水状态进行对比，分析不同排水量状态最佳浮态。基于“排水量-纵倾-航速-收到功率”数据图谱，选用双线性插值方法开发了船舶最佳纵倾计算软件，得到以下结论：

（1）相同排水量不同纵倾下船舶能耗具有一定差异，证明了浮态优化是船舶节能减排的有效可行手段；

（2）由于球鼻艏影响和船舶线型随吃水的变化，不同排水量下船舶最佳纵倾不尽相同，总体而言，适当首倾能耗较低；

（3）最佳纵倾计算软件可准确快速地求得船舶在特定排水量和航速工况下的最佳浮态及对应的首尾吃水，进而指导船舶配载调整，具有一定的工程应用价值。