废旧手机双回收渠道合作的演化博弈分析

王 健，谢欣雨

（福州大学经济与管理学院，福建 福州 350100）

一 引言

随着互联网的快速发展，智能手机在中国使用的范围愈发广泛，据iiMediaResearch（艾媒咨询）的数据显示，2021年我国智能手机的使用人数将突破8 亿人，达到8.12 亿人［1］。然而在每年出售5 亿部智能手机的同时，也会有将近3 亿部被淘汰积压［2］。废旧手机数量的激增，对国家生态环境和经济发展带来的危害已经引起了我国政府的高度重视。2016年3 月，我国已将废旧手机纳入《废旧电器电子产品处理目录（2014年版）》中，且出台了《生产者责任延伸制度推行方案》，明确了生产者在供应链上的主要责任，但是我国的废旧手机回收数量仍然不容乐观。废旧手机的丢弃会给国家和企业带来巨大的经济损失、资源浪费和环境污染，因此对废旧手机进行合理高效的回收利用迫在眉睫［3］。

目前我国废旧手机等电子产品的回收处理系统并不健全，回收的渠道主要包括正规回收渠道与非正规回收渠道，正规回收渠道是指以制造商和零售商回收为主体，制造商和零售商主要通过“以旧换新”政策来回收手机，以制造商为主体的回收模式优势在于对产品全周期的了解以及先进的技术，可以从源头上提高废旧手机的回收效率［4-5］。零售商可以直接激励消费者进行废旧手机的回收并掌握着市场资源［6］。非正规回收渠道是指除零售商和制造商以外的其他回收主体，主要包括专业的回收公司（不包括制造商和零售商的外包业务）以及市场上零散的商贩，非正规渠道回收商注重在回收时进行分工协作，通过回收技术和较好的规模经济来提升整条供应链的回收效率［7］。目前，回收商回收手机的处理方式主要有翻新、原材料回收和零部件回收［8］。近年来，由于翻新电子产品再次流向市场带来了很多重大事故，所以政府要求正规渠道回收商不再对手机进行翻新处理，但是对非正规渠道回收商的行为却无法控制［9］。中国居民废旧手机的处置渠道主要是闲置储存在家、赠予他人使用或者卖给街巷中回收手机的摊贩［10］。因为现在消费者使用的智能手机包含很多个人信息，消费者担心个人信息泄露，所以不愿出售废旧手机。愿意出售手机的消费者更多选择将废旧手机出售给非正规渠道回收商的原因是正规渠道回收商与非正规渠道回收商回收的价格差别太大，因此，正规渠道回收商能够获得的废旧手机数量相当有限。

对于逆向物流回收的研究主要有回收模式以及定价策略两个方面。对于回收模式的研究，姚卫新［11］将回收模式分为第三方负责回收、制造商负责回收、零售商负责回收三种模式，并在需求函数为线性函数的情况下进行建模分析。魏洁［12］则利用非线性需求函数对三种回收模式进行建模分析。温小琴［13］等学者考虑了制造商回收、零售商回收、第三方物流回收三种模式，并建立了以CSR 为基础的数学模型对三种模式进行优化求解。公彦德［14］等学者构建了以制造商和销售商为主导的制造商与销售商两者混合回收模式，以及制造商、销售商和第三方三者混合回收的4 类逆向供应链模型，运用博弈理论进行求解。

对于回收定价策略的研究，丁杨科［15］等学者通过Stackelberg 博弈模型，探讨在垄断回收和竞争回收两种模式下，废旧电子产品再制造逆向物流的定价决策。王喜刚［16］从社会福利最大化的视角出发，建立Stackelberg 博弈模型，探究回收废旧产品最合适的价格和政府补贴。蹇明［17］等学者建立了具有价格竞争的两个回收商之间的静态定价决策模型、再制造商与回收商之间的动态定价模型，以及再制造商的信息泄露决策模型，在分析再制造商信息泄露产生机理的基础上，给出了再制造商和第三方回收商的最优定价策略。

目前，我国学者对废旧手机逆向物流的研究都是将正规回收渠道和非正规回收渠道视作竞争关系，但是却没有考虑两者如若合作所带来的经济效益、安全效益以及环境效益。基于此，本文运用演化博弈的方法分析正规回收渠道和非正规回收渠道在合作方面的演化策略，探讨合理的超额收益分配、政府补贴分配，以及合作成本分摊，促进正规回收渠道和非正规回收渠道的合作，以丰富双渠道回收合作方面的理论研究。

二 正规回收渠道与非正规回收渠道的合作博弈分析

演化博弈是将博弈论中的分析方法与动态演化过程结合起来，使博弈一方根据另外一方的行为来对自身进行动态调整，从而在博弈中获取自身的最大收益。在博弈过程中，双方无法做到完全的理性，这就需要不断地演化和学习，并且学习的行为具有多样性和复杂性，最终找出利益最大化的决策方案［18］。

（一）模型设定

在信息不对称的情况下，正规渠道的回收商可以选择与非正规回收渠道的个人或企业进行合作，以获得更多以及质量更好的废旧手机，从而通过将废旧手机拆解成零部件或原材料进行二次使用，以获得超额收益。非正规渠道回收商可以与正规渠道回收商进行合作得到正规渠道回收企业从政府获得的部分补贴。

在设置参数和构建模型前，进行以下假设。

1.正规渠道回收商和非正规渠道回收商都具有有限理性［19］，博弈双方制定策略时依据特定的传递机制而不是理性的选择，且博弈过程中信息不对称。

2.正规渠道回收商和非正规渠道回收商在经过反复博弈后，可以获得令双方都满意的结果。

具体的参数设置如下：

I1：表示在双方不合作时，正规渠道回收商可以通过回收废旧手机获得的收益。

I2：表示在双方不合作时，非正规渠道回收商可以通过回收废旧手机获得的收益。

ΔI：表示正规渠道回收商和非正规渠道回收商在选择合作时双方可以获得的超额收益。

S：表示正规回收渠道在回收废旧手机时所获得的政府补贴。

C：表示正规渠道回收商和非正规渠道回收商在进行谈判合作时发生的一系列可能的成本，只要有一方倾向合作，无论另外一方是否合作，倾向合作的一方一定会产生一些前期投入。

α：是指正规渠道回收商和非正规渠道回收商在选择合作时，正规渠道回收商能够获得超额收益的比例。同理，1－α表示非正规渠道回收商能够获得超额收益ΔI的比例。

β：是指正规渠道回收商和非正规渠道回收商在选择合作时，正规渠道回收商能够获得政府补助的比例。同理，1－β表示非正规渠道回收商能够获得政府补助S的比例。

γ：是指正规渠道回收商和非正规渠道回收商在选择合作时，正规渠道回收商需要分担促进合作成本C的比例。同理，1－γ表示非正规渠道回收商需要分担促进合作成本C的比例。

当正规渠道回收商选择合作时，不仅可以获得原有的I1的收益，还可以获得超额收益αΔI，但是需要支付γC以及分配（1－β）S 给非正规渠道回收商；当非正规渠道回收商选择合作时，不仅可以获得原有的I2的收益，还可以获得超额收益（1-α）ΔI以及正规渠道回收商分配的βS，但是需要支付（1-γ）C；当正规渠道回收商选择不合作时，只能获得原有收入I1和政府补助S；当非正规渠道回收商选择不合作时，只能获得原有收益I2。根据演化博弈理论的基本思想建立如表1 的支付矩阵。

表1 博弈双方的支付矩阵

由支付矩阵可以得出正规渠道回收商选择合作时，它的期望收益：

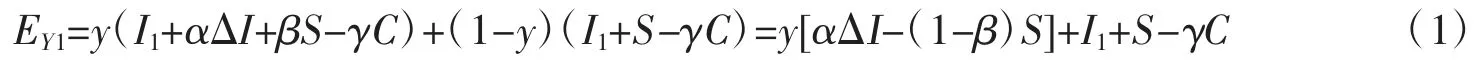
正规渠道回收商选择不合作时，它的期望收益：

正规渠道回收商的平均期望收益：

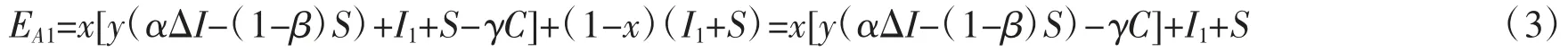
由式（1）和式（3）可得正规渠道回收商选择合作时的复制动态方程：

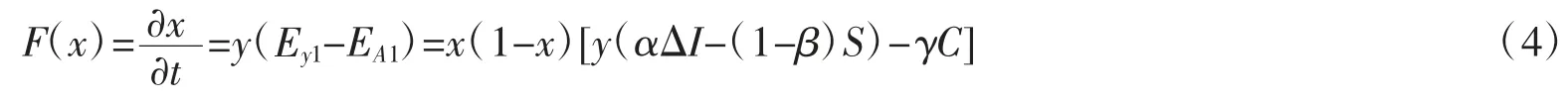
由支付矩阵可以得出非正规渠道回收商选择合作时，它的期望收益：

非正规渠道回收商选择不合作时，它的期望收益：

非正规渠道回收商的平均期望收益：

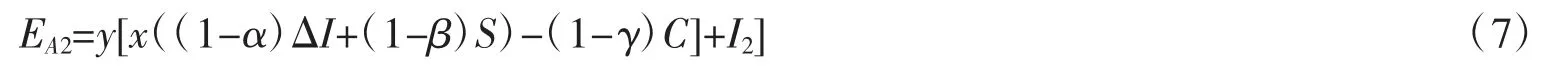
由式（1）和式（3）可得正规渠道回收商选择合作时的复制动态方程：

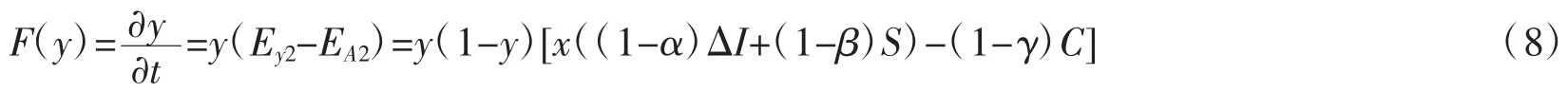
复制动态方程可以反映博弈双方的交互行为以及策略博弈的方向和速度，当博弈双方的复制动态方程均为 0 时，这时复制动力系统形成了均衡状态。因此，分别令 F（x）=0，F（y）=0，可得系统的均衡点：（0，0）（0，1）（1，0）（1，1）（x*，y*），其中：

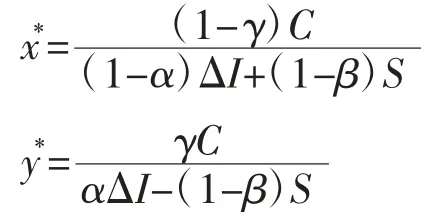
根据 Friedman［20］提出的方法，可分别对 F（x）和 F（y）求关于 x，y 的偏导，可以得到复制动态方程的雅克比矩阵J 的行列式和迹：

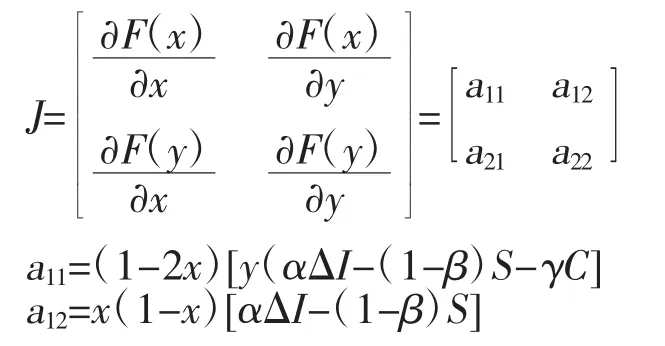
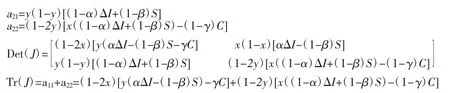
将均衡点（0，0）（0，1）（1，0）（1，1）（x*，y*）分别带入Det（J）和Tr（J），可得表2。

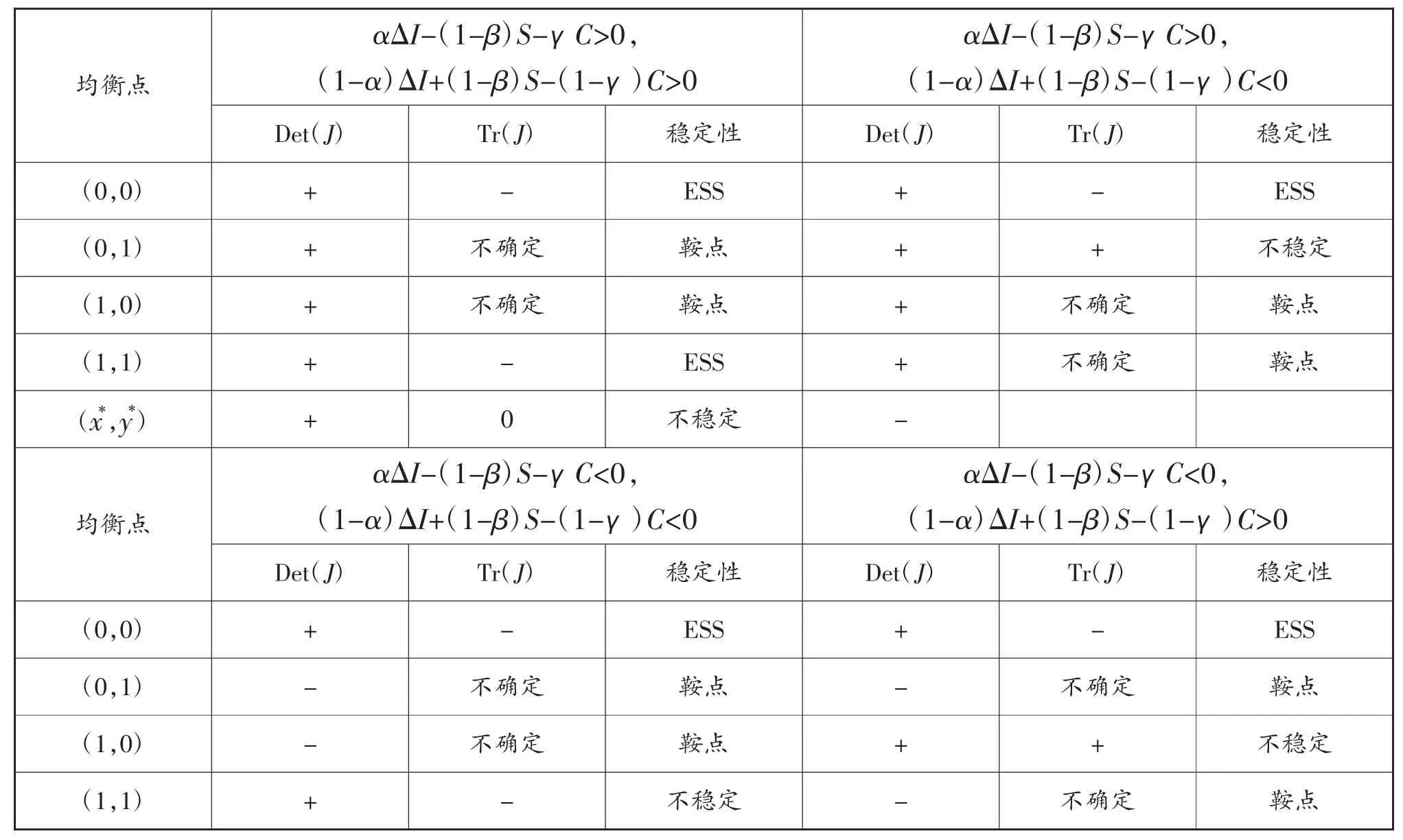
表2 局部稳定性结果分析

从表 2 可以看出，只有点（0，0）和点（1，1）达到了演化均衡点，（1，0）和（0，1）点没有达到演化均衡点，不具有稳定性，（x*，y*）点是一直在变化的。通过正规回收渠道和非正规回收渠道的合作博弈过程可以画出如图1 所示的相位图。

图1 正规回收渠道和非正规回收渠道合作动态演化路径

图1 清晰描绘了正规回收渠道和非正规回收渠道的动态演化博弈过程，横轴表示了正规回收渠道采取合作策略的概率，纵轴表示了非正规回收渠道愿意合作的概率。从图1 可以看出，ADB 是条临界线。

（1）当 αΔI-（1-β）S-γC>0，（1-α）ΔI+（1-β）S-（1-γ）C<0；αΔI-（1-β）S-γC<0，（1-α）ΔI+（1-γ）C<0；αΔI-（1-β）S-γC<0，（1-α）ΔI+（1-β）S-（1-γ）C>0；时，无论初始状态如何，系统都会趋于演化稳定点（0，0），这时由于双方不能达到共赢，正规回收渠道和非正规渠道都会采取不合作的策略。

（2）当 αΔI-（1-β）S-γC>0，（1-α）ΔI+（1-β）S-（1-γ）C>0 时，正规回收渠道和非正规回收渠道获得的额外收益均大于其自身付出的成本，这时双方会采取合作的策略。这时（0，0）（1，1）是双方博弈演化的稳定点，代表着系统存在两条演化路径，即正规回收渠道和非正规回收渠道存在可采取合作与不合作两种策略。博弈双方分别从（0，1）（1，0）两个不稳定点有两条演化策略，一条是从不稳定点沿着鞍点（x*，y*）向O 点演化，最终到达稳定点O（0，0）；另外一条演化路径是从不稳定点沿着鞍点（x*，y*）向C 点演化，最终到达稳定点 C（1，1）。

（二）模型中各影响要素进一步分析

通过对演化博弈的模型分析得到，正规回收渠道与非正规回收渠道选择是否合作的主要原因有：合作收益、合作成本、政府补贴以及这三者的分配比例。从图1 可以看出，系统采取哪种策略取决于区域AOBD的面积S1和区域ADBC 的面积S2［21］。这两个区域的面积由各参数决定，接下来讨论参数对面积的影响。

三 算例仿真

假设双方获得的超额收益ΔI 在200 万元到220 万元之间，政府补贴S 在15 万元到25 万元之间，合作成本在35 万元到45 万元之间。

（一）超额收益、政府补贴和博弈成本对演化策略的影响，如图2 所示。

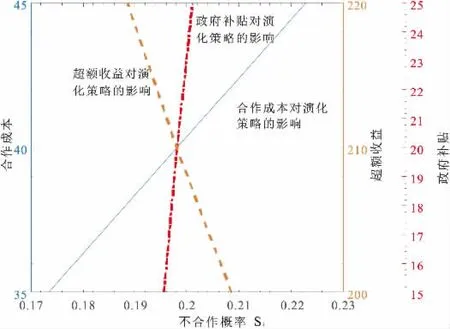
图2 超额收益、合作成本、政府补贴对不合作概率的影响

给定初始值进行仿真，令 ΔI＝210、S＝20、C＝40、α＝β＝γ＝0.4

由图2 可以看出，随着博弈成本和政府补贴的增大，正规回收渠道与非正规回收渠道不合作的概率渐渐增大；当超额收益不断增加时，双方不合作的概率渐渐变小，正规回收渠道与非正规回收渠道选择合作策略，与上述分析一致。

（二）各因素的分摊比例对演化策略的影响

1.超额收益分摊比例对演化策略的影响，如图3 所示。

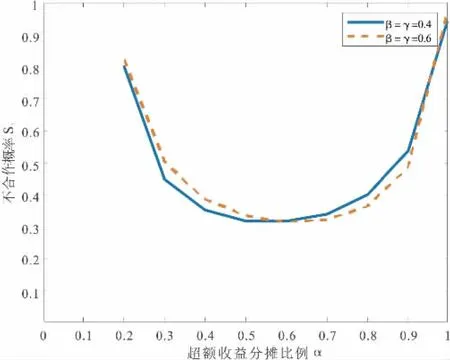
图3 超额收益分摊比例对不合作概率的影响

保持上述基本的参数不变，通过数值仿真分析在不同的成本分摊比例和政府补贴的分摊补贴比例中，超额收益的分摊比例对演化策略的影响，通过图3 可以发现，当β＝γ＝0.4 和β＝γ＝0.6 时，不同的超额收益分摊比例中不合作的概率S1交于同一点，说明存在一个合适的超额分摊比例α 使得不合作概率达到最小。当α<0.6 时，正规回收渠道和非正规回收渠道不合作的概率随着超额收益分配比例的增加而减少；当0.6<α<1 时，正规回收渠道和非正规回收渠道不合作的概率随着超额收益分配比例的增加而增加。

2.政府补贴的分摊比例对演化策略的影响，如图4 所示。

图4 政府补贴分摊比例对不合作概率的影响

保持上述基本的参数比例不变，通过数值仿真分析在不同的成本分摊比例和超额利润分摊比例过程中，政府补贴的分摊对演化策略的影响。从图4 可以看出，当α=γ=0.2 时，正规回收渠道和非正规回收渠道不合作的概率随着政府补贴分配比例的增加而减少，而当α=γ=0.8 时，正规回收渠道和非正规回收渠道不合作的概率随着政府补贴分配比例的增加而增加，与上述分析一致。

3.成本分摊比例对演化策略的影响，如图5 所示。

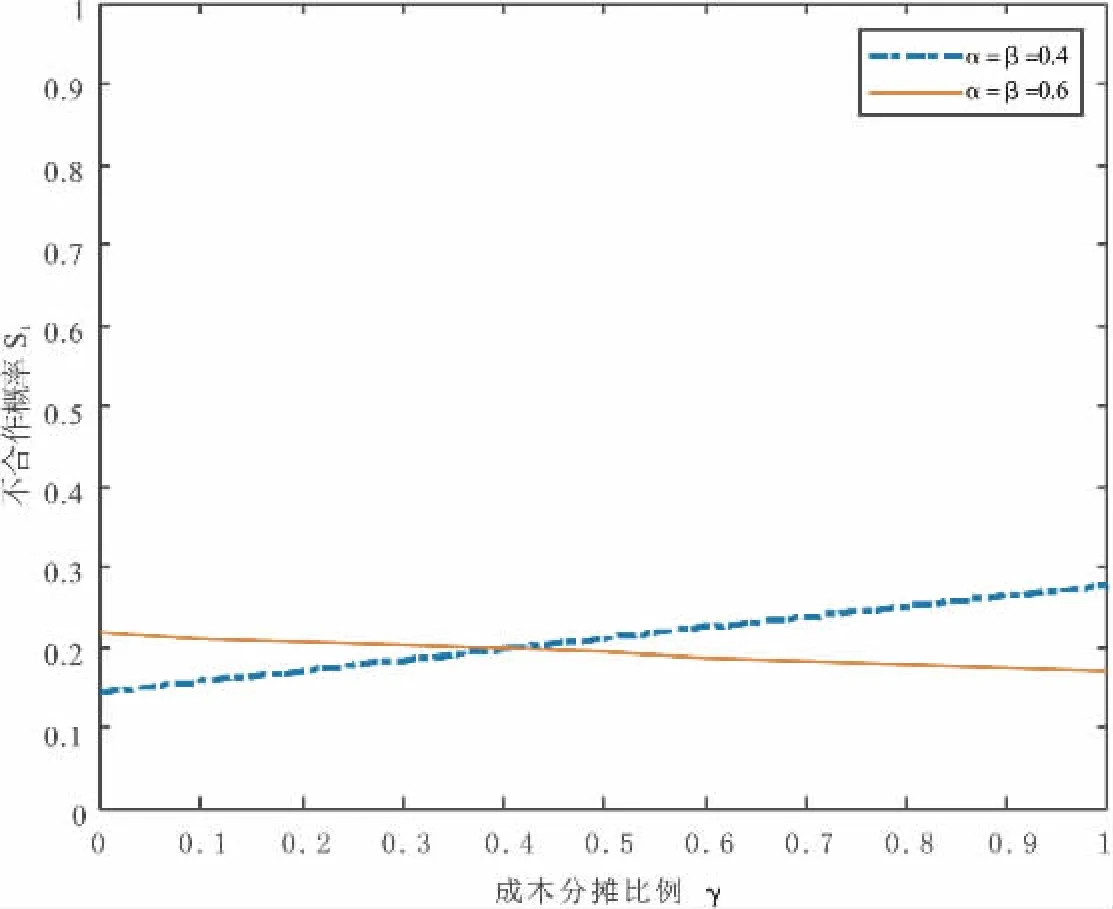
图5 成本分摊比例对不合作概率的影响

保持上述基本的参数不变，通过数值仿真分析在不同的政府补贴的分摊比例和超额收益的分摊比例过程中，成本分摊比例对演化策略的影响。从图 5 可以看出，当 α=β=0.4 时，满足 αΔI-（1-β）S<（1-α）ΔI+（1-β）S，此时正规回收渠道和非正规回收渠道不合作的概率随着政府补贴分配比例的增加而增加，而当α=β=0.6 时，满足 αΔI-（1-β）S>（1-α）ΔI+（1-β）S，正规回收渠道和非正规回收渠道不合作的概率随着政府补贴分配比例的增加而减小，与上述分析一致。

四 结论与建议

通过构建双方合作的演化博弈模型，并通过模型的演化过程分析发现，正规回收渠道和非正规回收渠道合作博弈的超额收益、合作成本、政府补贴以及这三者的分配比例对系统的演化路径有着不同的影响。

（1）超额收益与合作概率呈现正相关关系。（2）合作成本与合作概率呈现负相关关系。（3）政府补贴在超额收益和合作成本分配比例在（0，0.5）之间与合作概率呈现正相关关系，在（0.5，1）之间与合作概率呈现负相关关系。（4）存在一个超额收益分配比例使得合作概率最大。（5）当 αΔI-（1-β）S<（1-α）ΔI+（1－β）S 时，合作成本分摊比例与合作概率呈负相关关系，当 αΔI-（1-β）S>（1-α）ΔI+（1－β）S 时，合作成本分摊比例与合作概率呈正相关关系。（6）政府补贴分摊比例在超额收益和合作成本分配比例处于（0，0.5）之间时，其与合作概率呈现正相关关系，处于（0.5，1）之间时，其与合作概率呈现负相关关系。

正规回收渠道对回收的废旧手机能够进行专业安全的处置，但回收数量有限。根据调查，正规回收渠道的废旧手机的回收率还不到2%；非正规回收渠道回收废旧手机数量较多，但是对于回收的废旧手机处置不够专业。所以双方应该认识到彼此的互补优势，增强合作意图，构建完善的合作体系。政府应该加强激励和扶持，促进双方进一步合作。