数学概念教学的四个视角——以“长方形和正方形的面积计算”的教学为例

江苏省无锡市梅村实验小学 沈秋喜 钱艳妮

数学概念在建构学生知识体系的过程中起着举足轻重的作用，它直接影响着学生的运算能力、逻辑思维、空间想象和实践创新等一系列核心素养的培养和提升。研究数学概念内涵的关键在于对数学概念本质的理解和把握，然而概念的高度抽象性、概括性成为学生学习过程中的拦路虎。因此如何有效地进行数学概念教学就成为数学教学研究不变的主题。下面笔者就以苏教版数学三年级下册“长方形和正方形的面积计算”的教学为例，谈谈具体的做法。

一、创设真实情境，感悟概念本质

（一）在真实情境中唤醒已有经验

数学知识的学习不再是简单的掌握知识，而是要以知识为载体培养学生的学习能力，培养学生用数学的眼光观察世界。因此，教师在创设教学情境时，可以选择学生熟悉的、与真实生活相关的情境作为切入点，让学生体会到原来生活中存在着许多与数学相关的现象，感受到数学与生活的密切联系，激发学生学习数学的兴趣。例如，上课伊始，笔者创设小羊们玩俄罗斯方块游戏的情境，并从游戏中选取3 种形状不同的图形（如图1）。

图1

学生借助1 平方厘米的小正方形去估算这些图形的面积。学生在观察比较中发现，虽然这些图形的形状各不相同，但它们的面积都是4 平方厘米。从而让学生体会到面积作为事物的一种属性，和长度一样是可以度量的，并初步感受图形面积的大小和单位面积的小正方形的个数有关，为后续学习长方形面积奠定基础。

（二）在真实情境中提出驱动性问题

驱动性问题能激发学生的注意力，使其主动投入数学知识的探索中，学生通过解决问题能促进对知识本质的深度理解。在驱动性问题的引领下，学生自主产生学习的内在动力，从而在多个维度进行持续思考、自主探索。在教学过程中，设计小羊们想知道长方形油菜花田面积的驱动性问题，引发学生思考：当长方形的面积很大时，再用单位面积的小正方形去测量就变得不太现实，有没有更好的方法可以知道长方形的面积呢？学生凭借已有的生活经验和敏锐的直觉猜想：长方形的面积与长方形的长和宽有关。甚至有学生说出长方形的面积就是用长乘宽。但是“为什么长方形的面积是用长乘宽来计算的呢”？学生还处在知其然而不知其所以然的认知层面，笔者通过引导学生探究来寻找长方形面积背后更为本质和核心的概念或思想。

二、经历深层想象，领悟概念本质

想象是人脑对已有的表象经过加工、改造，产生新的表象和思维的过程。在教学中，教师不仅要让学生掌握面积计算的方法，更要让学生感悟面积的本质含义，引导学生的思维走向深处。如果只是用1 平方厘米的小正方形摆几个长方形，或用1 平方厘米的小正方形去铺满已知长、宽的长方形，再从数据与图形的直观比较中直接得出长方形的面积计算公式，那么操作只是停留在摆一摆、数一数、算一算的直观现象展示上，学生并没有真正理解为什么长方形的面积和长与宽有关。为了让学生真正深入探究过程，笔者引导学生进行合理的深层想象，充分理解这里的长、宽分别代表的是每个单位面积个数和行数，让学生思维从一维长度向二维面积发展。

（一）密铺——具象

师：如何求出这个长方形的面积呢？踏实、认真的暖羊羊首先想到了摆一摆的方法，如图2。

图2

师：这个长方形里包含了几个小正方形？

生：12 个。

师；你是怎么知道的？

生：4×3=12（个），12 个1 平方厘米的小正方形，所以面积就是12 平方厘米。

师：这里的4 指的是什么？3 指的又是什么呢？

生：每排摆4 个，摆了3 排。

师：那么如何求小正方形的个数呢？

生：用每排个数×排数求出小正方形的个数是12个，所以面积就是12 平方厘米。

（二）“半铺”——半抽象

师：爱动脑筋的美羊羊，只用了6 个小正方形就知道了长方形的面积。你知道它是怎么摆的吗？

生：沿着长摆4 个，沿着宽摆3 个，如图3。

图3

师：为什么这样摆也能求出长方形的面积呢？

生1：沿着长摆4 个。

生2：沿着宽摆3 排。

师：仔细观察，这里的每排个数和排数分别和长方形的什么有关呢？

生：长方形的长就是每排个数，长方形的宽就是排数。

（三）想象——抽象

师：喜羊羊也发现了这个秘密，但它一个都不用摆，就能知道长方形的面积。你知道它是怎么想的吗？

图4

生：如图4，长4 厘米，宽3 厘米，面积就是4×3=12平方厘米。

师：为什么4×3 就是面积呢？

生：沿着长可以摆4 个，沿着宽能摆3 排，一共有12个小正方形，所以它的面积就是12 平方厘米。

师：这里的长是4 厘米就是有4 个1 厘米，每个1厘米就可以想象成1 个小正方形。宽是3 厘米就可以想象成3 个小正方形。

师：看来每排个数和排数确实和长方形的长和宽有关。为什么用长×宽就能求出长方形的面积呢？

生：长就是每排个数，宽就是排数，长方形的面积就等于长乘宽。

由于学生在认识面积意义时，已经有用单位面积的小正方形铺满长方形的操作经验，所以在用情境唤醒学生已有的经验后，可以让学生通过想象经历用1 平方厘米的小正方形分别把长方形铺满，再到“半铺”，最后到不铺的完整过程。第一，在“铺满”中发现，要知道长方形的面积，只要知道小正方形的个数，而小正方形的个数=每排个数×排数，初步感知长方形的面积与长方形的长和宽有关；第二，在“半铺”中发现每排个数对应长方形的长，排数对应长方形的宽，体会长方形的面积与长方形的长和宽有关；第三，在“想象”中揭示长方形的面积与长方形的长和宽的关系；第四，在深层思考中推理出长方形的面积公式。学生的思维从具象到半抽象，再到抽象，层层递进，反复感受，充分感悟图形的面积需要两个维度的数值来刻画的特点。学生掌握了推理长方形面积公式的方法后，正方形的面积公式可以用由此及彼的推理方式得到。

三、借助多次推理，凸显概念本质

推理是数学的基本思维方式，是发展学生用数学的思维思考世界的重要途径。在推理的过程中，考查的对象数量越多，那么推理的过程就会更加深入，结论的可靠性也更强。有效利用几何画板的可变化的特点，创设丰富的表象为合情推理提供更多的例子，而后推理出长方形和正方形的面积公式。可以分为4 个阶段推进（如图5）：

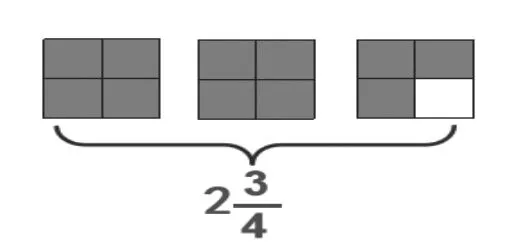
图5

（1）宽保持不变，长变大；（2）长保持不变，宽变大；（3）长和宽同时变大；（4）想象超出屏幕更大的长方形。长和宽在不断地变化，学生进行对应的想象：沿着长摆几个，沿着宽摆几个，一共有多少个单位面积，面积是多少，把学生的思维由“长方形的面积=每排个数×排数”抽象到“长方形的面积=长×宽”。借助多媒体课件连续改变图形的长和宽，让学生直观地看到长和宽与面积之间的联系，使得学生对面积的认识不只停留在公式的记忆上，而是对面积的本质有了更深刻的理解，即图形中面积单位的总个数。此时，学生的思维更加清晰，推理的空间也变得更为广阔，从有限走向无限，从而增加了推理所得结论的可靠性，也让学生的推理思维得到发展。

四、内化提升练习，深化概念本质

数学知识的学习过程，必须遵循数学学科特性和学生的认知规律，通过不断地分析、综合、运算、推理、判断来完成。因此，练习在考虑基础性、针对性的同时，应体现面积本质的应用，有利于学生深化理解，形成技能。因此，本节课设计了如下练习。

（1）图6 中每个小正方形表示1 平方厘米，你能算出长方形的面积是多少平方厘米吗？

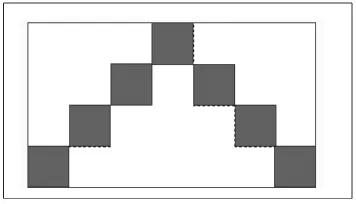
图6

（2）如图7，你能知道这张照片原来的面积是多少吗？

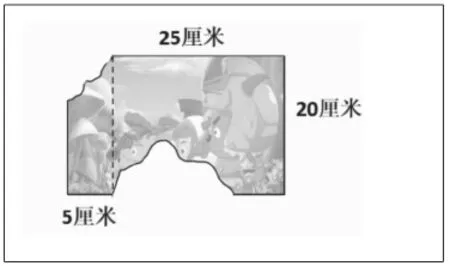
图7

（3）思考：村主任用18 米长的篱笆围一个长方形的花坛，这个长方形可能是怎样的？你能分别求出它们的面积吗？

练习的设计不但要对教材中的习题进行有效的利用和整合，还要设计有层次、有梯度的练习。第（1）题是基础题，可以帮助学生巩固对长方形和正方形面积计算公式的理解和应用；第（2）题是变式题，可以促进学生灵活运用知识解决问题的能力的提升。在这两个练习中，长方形的长和宽并没有直接出示，而需要学生通过观察并推断出长和宽后，才能利用面积公式计算出长方形的面积。第（3）题是拓展题，可以让学生的思维“跳一跳”，提升数学思维品质。特别是最后一问，周长和面积本身就是易混淆的两个概念，学生通过思考得到4 种不同的长方形，在对比和观察中发现，虽然长方形的周长不变，但长和宽都在变化，所以面积也在不断地变化，从而更深入地理解面积的本质。教师继续以此为推理的基础材料，引导学生进一步思考：宽还能继续变小吗？学生意识到宽还能变成更小的1 分米，那么长就是89 分米。教师以此为思考点，最后提出两个问题：（1）照这样能变成多少个不同的长方形？宽逐渐接近几？这时长又有什么变化呢？（2）如果两个长方形中的宽分别为1 分米、1 厘米，我们又该如何用以米作单位的小数来表示？这时我们又可以用怎样的小正方形来测量面积呢？在这样的深度思考中,不仅渗透了趋于无穷的极限思想，学生的思维空间也得到了扩大，思维的自由度得到了提升。让思维向深处漫延，也是为小数范围面积计算的理解埋下伏笔。

综上所述，数学概念教学应抓住概念的本质属性，充分借助想象和推理展开探索过程，在探索的过程中促进对本质属性的理解和内化，从中汲取思维的力量，帮助学生成为心智自由的学习者，进而发展学生的数学核心素养，为学生的终身发展奠定坚实的基础。