基于S -A湍流模型的Runge -Kutta有限元算法

曹鹏程， 廖绍凯,2， 张 研， 陈 达

(1.嘉兴学院 建筑工程学院，嘉兴 314001； 2.河海大学 力学与材料学院，南京 211100；3.河海大学 港口海岸与近海工程学院，南京 211100)

1 引 言

数值模拟钝体湍流绕流问题主要有直接数值模拟法(DNS法)、大涡模拟法(LES法)和基于雷诺时均方程模拟法(RANS法)三种方法[1]。相关数值算法的研究已成为众多学者的研究热点。

DNS法能够提供精确的解决方案，但是所需网格必须小于或等于流场中最小的漩涡结构尺寸，对计算机容量要求极高，计算量巨大，限制了其广泛应用[2]。LES法的计算效率相比DNS法要提高很多，已成功应用于求解各种形状的湍流绕流问题[3]，但近壁区域仍需要非常精细的网格。RANS法可在较低的计算成本下实现高雷诺数下的湍流计算[4]。与二方程RNGk-ε模型、修正的k-ε模型[5]和k-ω模型[6]相比，一方程S -A模型[7]具有求解方程较少的优点，可进一步降低计算成本。

近年来，基于一方程S -A模型的RANS法已成功求解了圆柱绕流和方柱绕流问题[8,9]，并大量运用在覆冰输电线绕流数值计算中[10,11]。目前求解RANS方程主要采用基于特征线分裂法(CBS法)和迎风有限元法(SUPG法)，以克服方程中的非线性项带来的数值振荡问题。值得注意的是，这些算法在时间离散上采用一阶离散格式[8,9]，因此，探索高阶离散格式和减少刚度矩阵的更新次数以提高计算精度、效率和收敛性，有待于进一步研究。

本文将基于一方程 S -A 模型封闭RANS方程，采用沿均匀流线的坐标变换，消除其非线性项，采用沿均匀流线的三阶Runge -Kutta法进行时间离散，采用Galerkin法进行空间离散，提出求解湍流模型的有限元算法。通过经典的算例，进一步验证算法的有效性、精度和收敛性。

2 基于S -A模型的有限元格式

2.1 控制方程

二维非定常不可压缩流的无量纲RANS方程和S -A模型的标量方程为

(1)

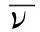
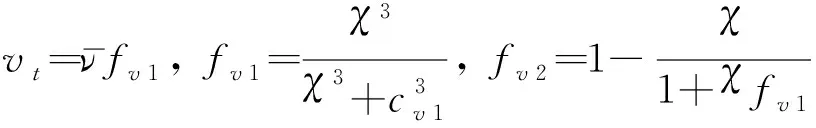
cb 1=0.1355，σ=2/3,cb 2=0.622

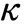
cw 2=0.3,cw 3=2，cv 1=7.1

由于式(1)含有非线性对流项，为非自伴随算子，当采用标准的Galerkin有限元方法进行空间离散时，得不到最优解。因此，采用经时间间隔Δt沿流线的坐标变换[12]，得到无对流项表达式为

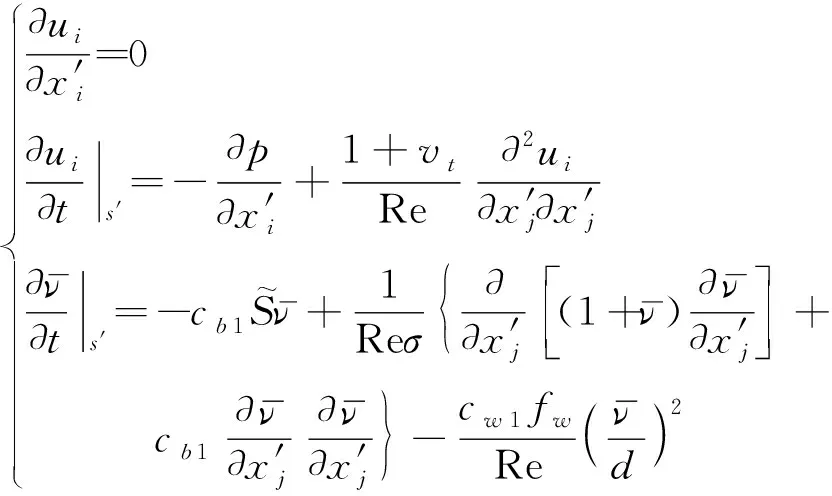
(2)

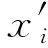
2.2 时间离散

(3,4)

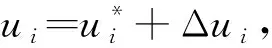
为了提高计算精度，基于沿均匀流线的三阶Runge -Kutta法对式(3)进行时间离散。假定已知tn时刻流场的速度和压力，则在给定的时间步长Δt=tn + 1-tn，tn + 1时刻中间辅助速度为

(5)

(6)

(7)

(8)

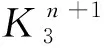
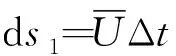
(9)

利用沿均匀流线的Taylor展开，并忽略其中的高阶小量，式(5～7)的相关动坐标系下的量转化为静坐标系下的量为

(10)

(11)

(12)

(13)

将式(10～12) 代入式(5)，可得中间辅助速度为

(14)

基于式(4)，可得tn + 1时刻的速度为

(15)

显然，求解式(15)前，需先求解tn + 1时刻的速度。为此，对式(15)两边取散度，并考虑tn + 1时刻的不可压缩条件，可得压力Poisson方程为

(16)

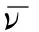
(17)

2.3 空间离散

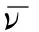
(18)

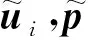
权函数采用式(18)的单元插值函数，乘以式(13，14，17)的两侧，并在计算域中进行空间积分，可得其弱积分格式为

(19)

(20)

(21)

式中

类似地，对式(15,16)加权积分后的弱积分形式为

(22)

(23)

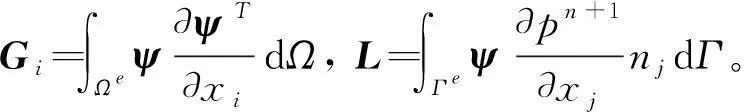
至此，获得了基于 S -A 模型的沿均匀流线的三阶 Runge -Kutta 法时间离散的有限元格式，其求解步骤归纳如下。

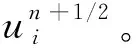
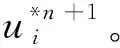
(3) 通过压力Poisson方程(23)，求得tn + 1时刻的压力pn +1。

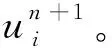
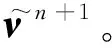
(7) 返回步骤(1)继续下一个时刻的计算。

3 算例应用与验证

3.1 方柱绕流

在流体动力学领域，方柱绕流是经典的湍流数值计算案例。文献[13-15]进行了实验研究，并获得了阻力系数、升力系数、Strouhal数和压力系数。Shimada等[16]采用两方程k-ε模型进行了相关的数值仿真模拟，文献[8，9]在S -A模型的基础上，提出了一阶时间离散有限元格式并进行了数值验算。下面将基于S -A模型的沿均匀流线的三阶 Runge -Kutta 法时间离散的有限元格式来模拟上述方柱绕流问题，以进一步验证该方法的有效性和计算精度。

典型的方柱无量纲模型和边界条件如图1所示，其中以方柱的边长取为特征尺寸和以左侧的来流速度为特征速度进行无量纲化。本次模型的计算域取为Ω=[-10,25]×[-10,10]，采用四边形四节点线性结构单元划分网格，网格数为41461，其中方柱近壁区域采用细网格进行划分，方柱表面布置了320个节点，表层单元厚度为0.002，方柱有限元模型如图2所示。

图1 方柱绕流模型和边界条件

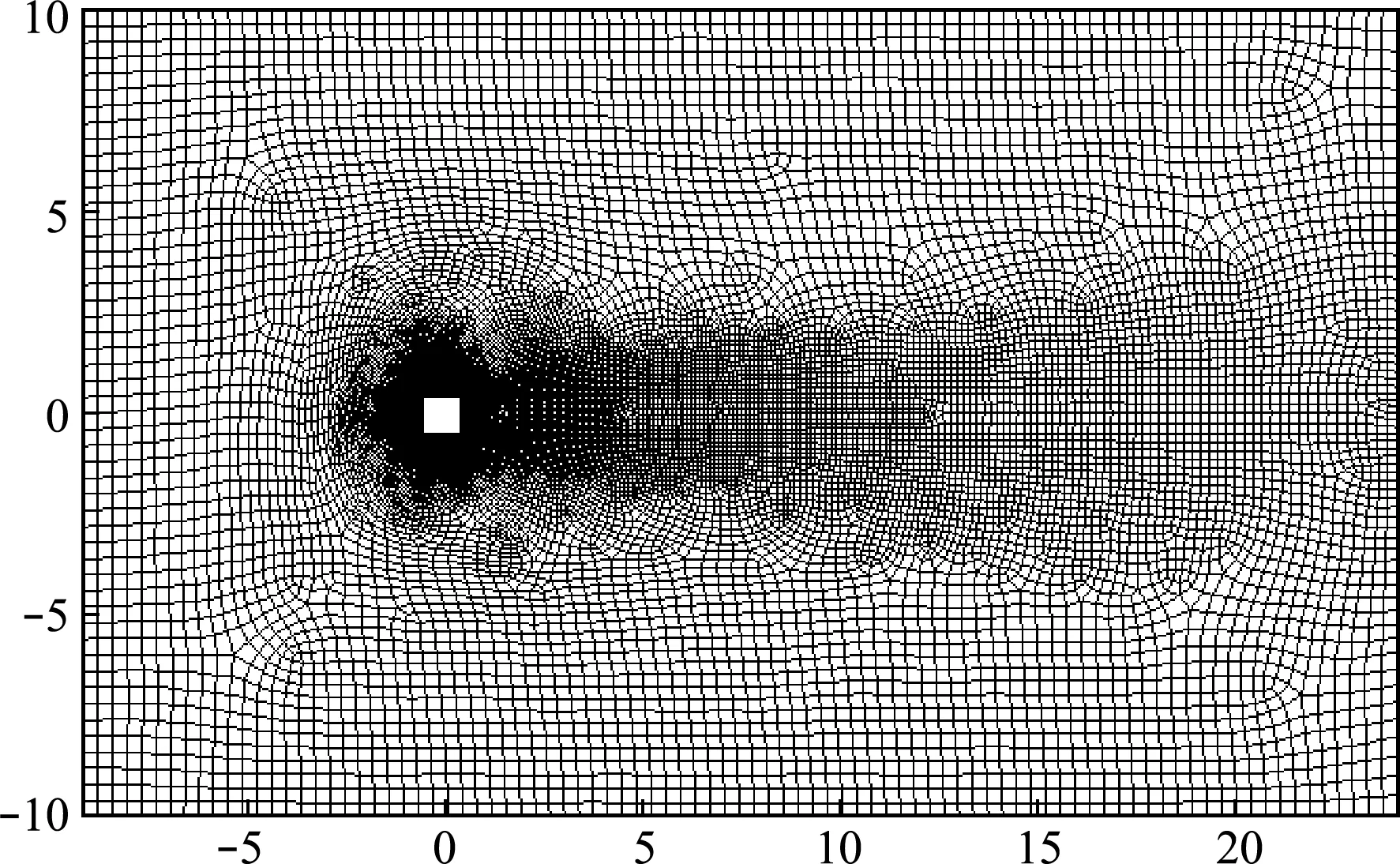
图2 方柱绕流有限元模型

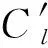
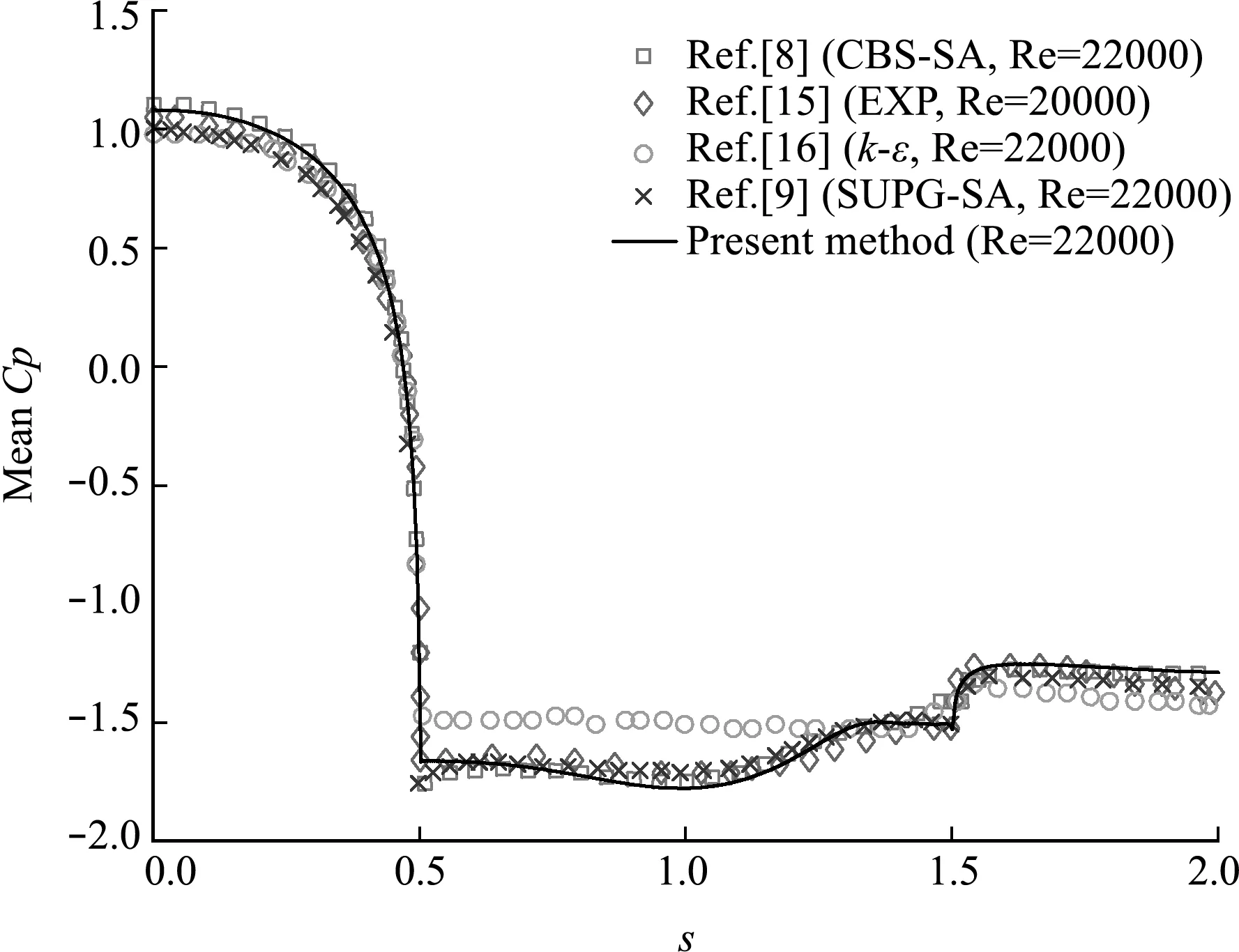
图3 平均压力系数分布图比较

图4给出了本文算法和文献[8]的阻力Cd和升力Cl时程曲线，可以看出，本文算法在无量纲时间30处已获得稳定的收敛解，而文献[8]的无量纲收敛时间为130，说明本文算法有助于提高算法的收敛性，具有较低的计算成本。

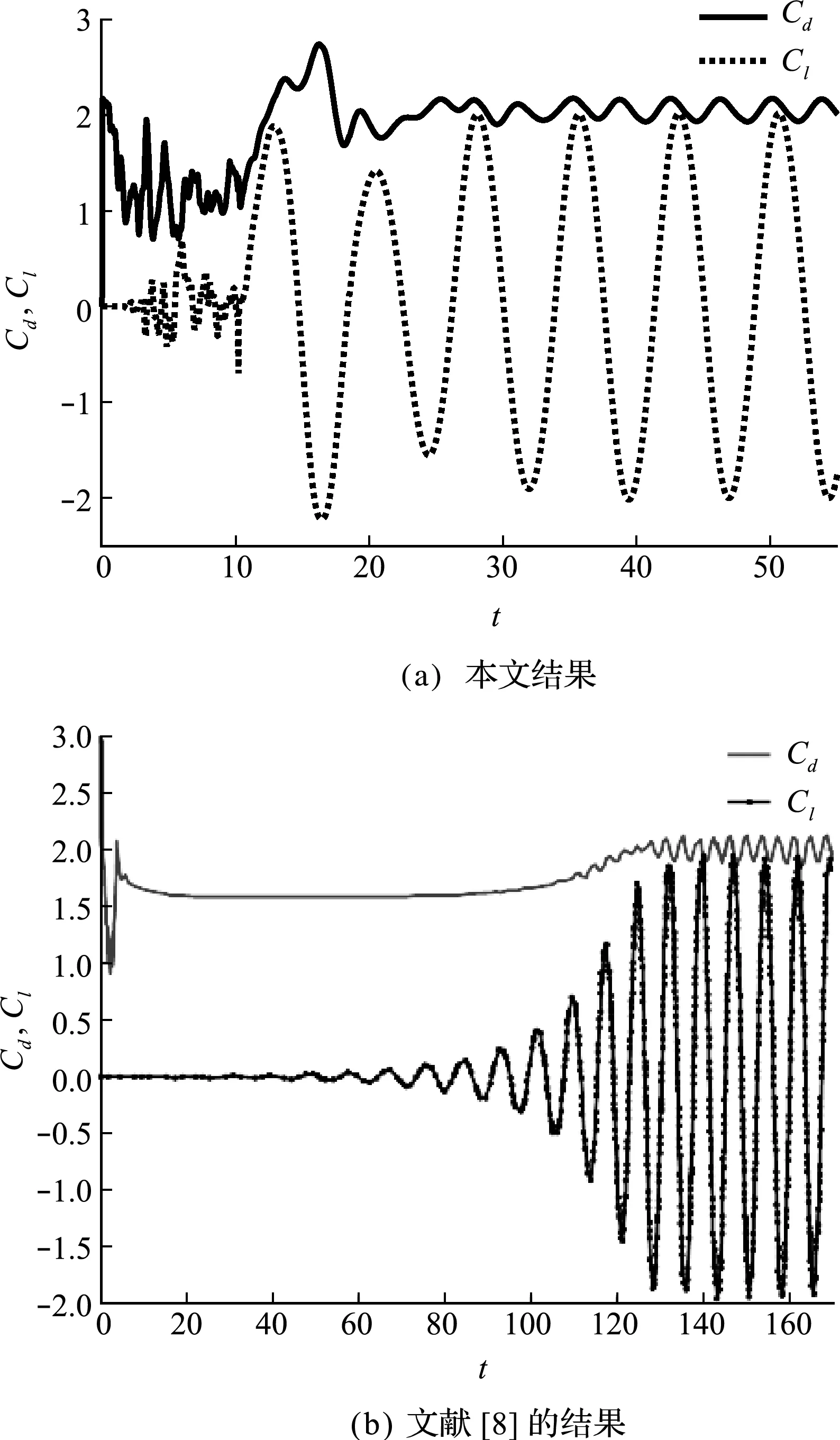
图4 阻力Cd和升力Cl时程曲线

3.2 覆冰输电线绕流

在冬季风、雨和雪冰冻等恶劣气象联合作用下，覆冰输电线受到风激励作用后产生流致效应，当满足特定条件后，覆冰输电线会发生一种低频率、大振幅的自激振动，严重威胁电力供应系统的安全运行。为此，众多学者致力于输电线覆冰情况下的气动系数及其演化规律的研究，可为舞动的判定提供基础性数据，具有重要的科学意义。

参照国标(LGJ GB1179-83)的型号规定，输电线为LGJ-240(直径D=26.8 mm)型号，并采用文献[17,18]以固定尺寸的小圆描述覆冰外形的顶端，小圆和输电线轮廓的大圆之间用切线连接描述覆冰的外形，通过移动小圆来控制覆冰厚度的新月形模型，本文考察覆冰厚度H=D的情况，如图5所示。

采用均匀来流风场，空气密度为1.25 kg/m3，动力粘度系数为1.72×10-5Pa·s，风速为10 m/s与文献[17]风洞试验的工况一致。通过以输电线圆心旋转覆冰输电线来表征风攻角，如图6所示。

本文数值模拟风攻角α从0°～40°(Δα=10°)的情况，并在气动力系数改变剧烈的地方进行加密计算。0°风攻角时覆冰输电线绕流无量纲化后的边界条件和网格如图7和图8所示。

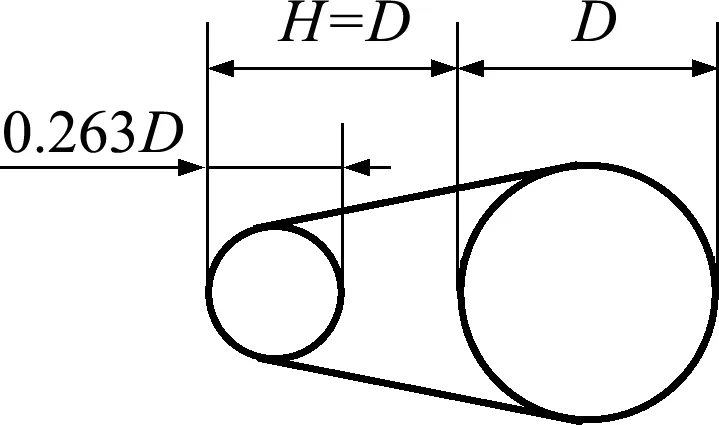
图5 新月形覆冰模型

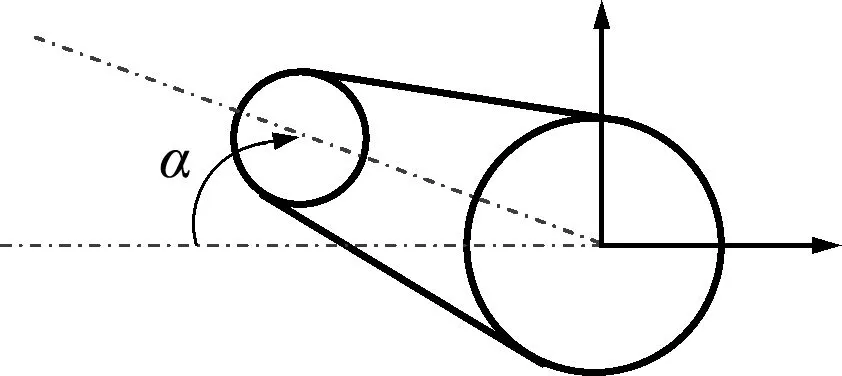
图6 风攻角

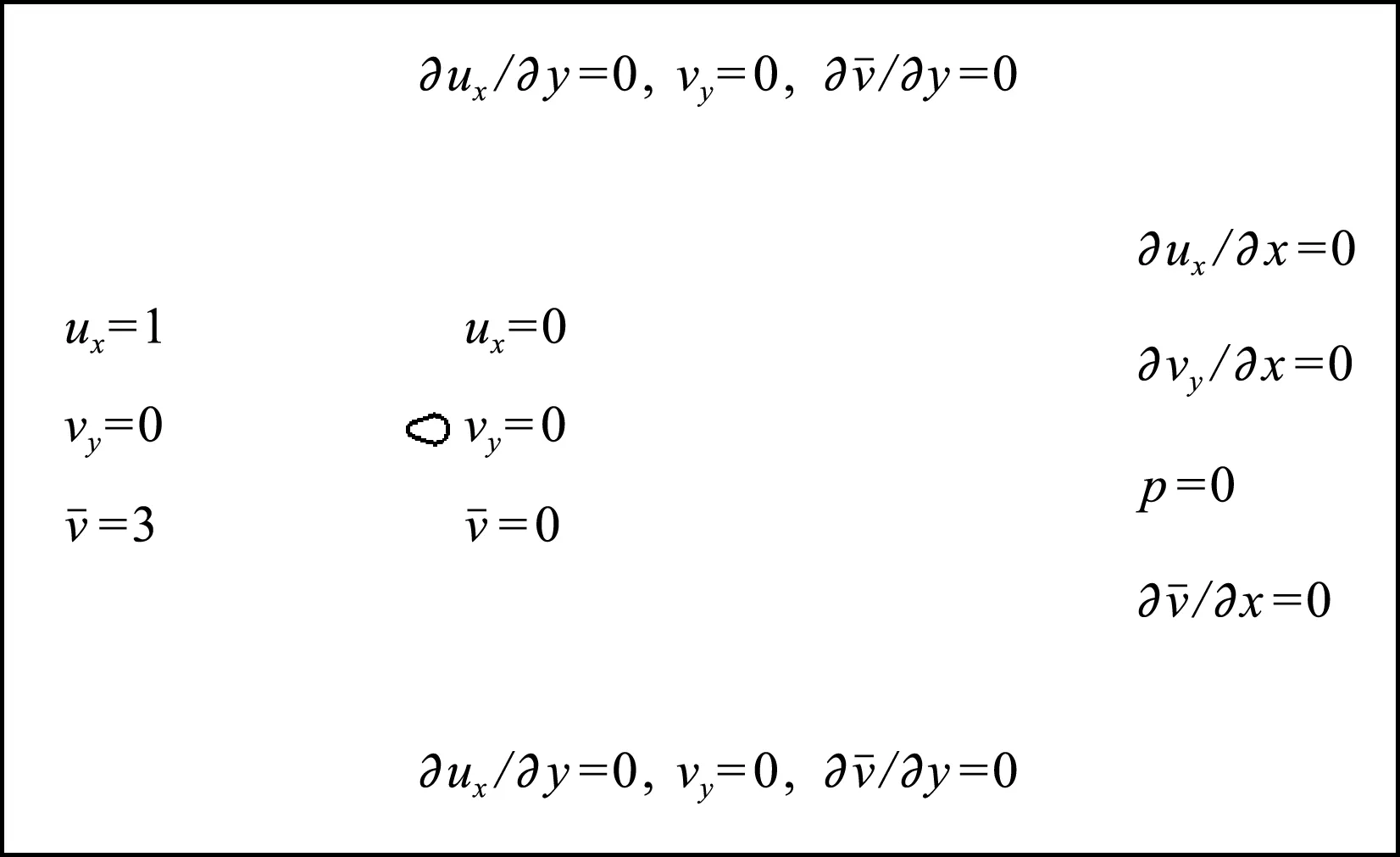
图7 覆冰输电线绕流边界条件

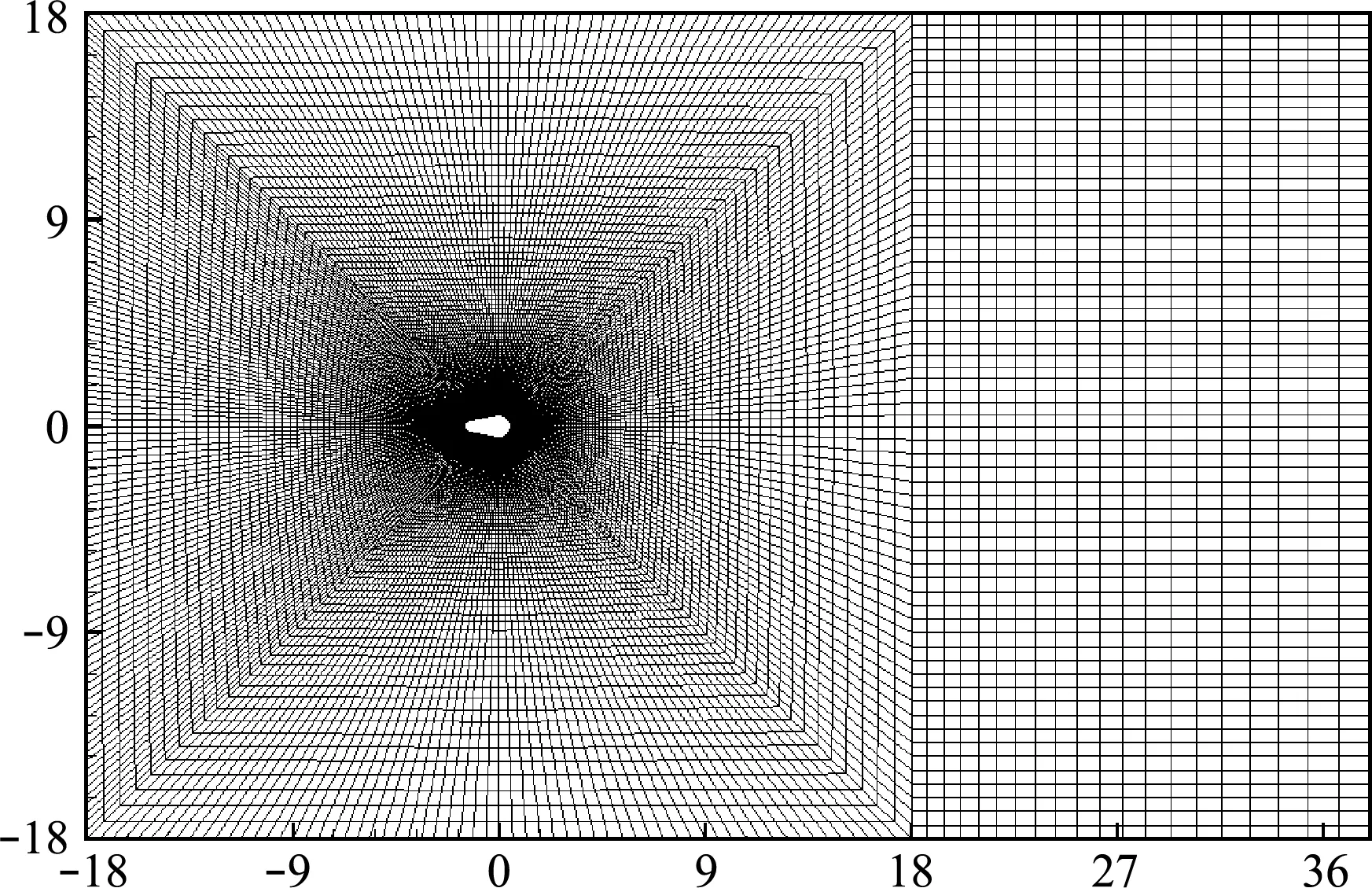
图8 覆冰输电线绕流网格划分

图9为采用本文算法得到的1.0D新月形覆冰输电线的平均阻力系数和平均升力系数随风攻角的变化关系，并将计算结果与已有的风洞试验和数值模拟结果对比分析。文献[17，19]通过风洞试验进行了相同风速下1.0D覆冰厚度的输电线气动力系数的测定，Shinichi等[18]基于LES模型对此进行了数值模拟。可以看出，本文的计算结果与试验和文献[18]数值模拟的结果基本保持一致，并很好地展现了升力系数尖峰突跳现象，这种尖峰突跳现象将给输电线路的稳定性产生影响，严重时将产生舞动现象。

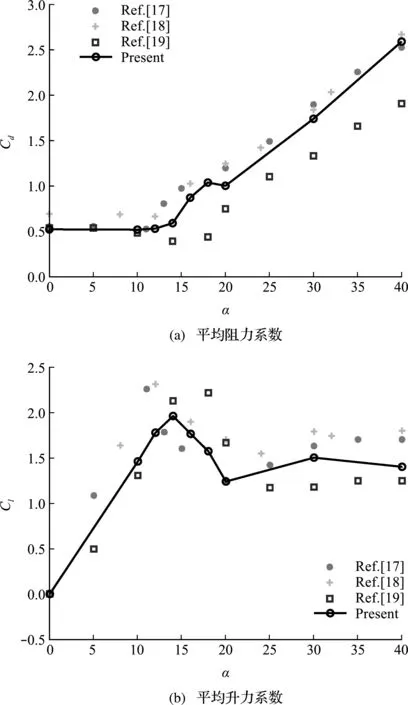
图9 气动力系数随风攻角的变化曲线比较

4 结 论

本文基于一方程 S -A 湍流模型封闭RANS方程求解湍流绕流问题。通过坐标变换得到了无对流项RANS方程，以使Galerkin法空间离散时获得最优解，时间离散时采用沿均匀流线的三阶 Runge -Kutta 进行离散，并利用Taylor展开将动作标系下的量转换成静坐标系下的量，建立了求解RANS方程的有限元算法。

基于本文有限元算法，数值模拟了经典的方柱绕流和覆冰输电线绕流问题。数值结果表明，得到的平均阻力系数和均方根升力系数与实验结果基本一致，且优于一阶时间离散算法的结果，表明该算法可以有效地预测湍流绕流问题，且有利于提高数值解的计算精度和收敛性。