大型户外广告牌面板极值风压分布的试验研究
2022-04-20汪大海黄洪量邓宇帆梁枢果邹良浩
汪大海, 黄洪量, 邓宇帆, 梁枢果, 邹良浩
(1.武汉理工大学 土木工程与建筑学院,武汉 430070; 2.武汉大学 土木建筑工程学院,武汉 430070)
1 引 言
户外单立柱广告牌是一种常见的高耸悬臂结构,其上部迎风面积相对较大,具有头重脚轻和轻柔等特点,其风灾破坏时有发生,是一类典型的城市风易损性结构。Tamura等[1]发现在风灾中广告牌结构易产生碎片,对人体或其他构筑物有造成二次伤害的危险。因此,国内外学者在这个方向开展了大量的研究。汪大海等[2]基于试验,为三面广告牌风荷载取值提供了可靠的试验数据和计算依据;赵雅丽等[3]在试验中发现脉动风压系数随湍流度增大而增大;顾明等[4]发现广告牌面板边缘附近的平均风压系数绝对值及脉动风压系数要比面板内部区域大;汪大海等[5]分析了风压时程,探究了广告牌面板上风压时程的分布特性;Wang等[6]通过风洞试验,测量了板表面的同步动压力,研究了局部压力、各单板和整体结构的整体力特性;Li等[7]通过气弹模型风洞试验,开展了双面广告牌的风振响应规律及理论算法的研究;申琪等[8]基于试验,开展了广告牌结构的风振系数和等效风荷载的研究。这些研究初步完善了三面广告牌结构的防灾设计理论,为风荷载的计算提供了一种理论方法。
研究还发现,由于气流在广告牌面板边缘会发生分离、涡流及再附等现象,会导致一部分广告牌面板上的风压时程呈现出明显的非高斯性。文献[9,10]指出结构边缘处的风压往往不符合高斯分布;文献[11,12]发现,与高斯风压相比,同等风速下的非高斯风压造成结构破坏的概率会提高15%~30%;全涌等[13]提出了一种基于块极大值的极值风压计算方法;吴凤波等[14]对非高斯风压极值估计时使用的矩转换法进行了对比研究;张爱社等[15]通过流体力学数值仿真方法考察了方柱结构表面瞬态风压分布特性。上述研究为完善三面广告牌结构的防灾设计方法提供了重要的借鉴。
目前,各国规范仅给出了单面板的设计风压取值,我国《建筑结构荷载规范(GB 50009-2012)》仅给出了单面板广告牌的顺风向的整体体型系数,未考虑风压的非高斯性及局部风压系数。美国荷载规范(ASCE/SEI 7-10)中,基于试验直接给出了单板的顺风向和扭转极值风压系数;对于三面广告牌这种特殊的多面板开敞式结构,若将所有面板的风压体型系数均按照单面板结构进行取值并不合理。
本文通过刚性模型的测压风洞试验,开展了典型三面广告牌面板在不同地貌类型下的面板风压测试,分析了面板风压时程的高斯/非高斯特性,采用三种方法给出了非高斯极值风压的分布特性。并考察了不同湍流度对极值风压的影响。此项研究对广告牌面板结构的设计风压体型系数的取值,以及广告牌面板的抗风易损性的研究提供了基础数据和计算方法。
2 广告牌结构的测压风洞试验
2.1 试验模型设计
三面单立柱开敞结构广告牌是我国常见的户外独立柱广告牌,此次试验模型的原型是由国家建筑标准设计图集《户外钢结构独立柱广告牌》(07SG526)的G3-6×18广告牌,参数列入表1。

表1 广告牌型号及总体参数
此次刚性模型采用λL=1∶20几何缩尺比制作模型进行试验,风洞阻塞率为4.85%,满足要求。考虑到风压分布在气流分离处的变化,本次试验在面板测点布置时采用边密中疏、中心对称的布置方式,单侧布置84个测点,总测点数为84×2=168。测压管从面板模型的支撑骨架和圆管立柱内走线,尽可能减少了测压管外形对风压测量精度的影响。本文试验中测压管长度均在1.3 m左右,符合《建筑工程风洞试验方法标准(JGJ/T 338-2014)》规定的要求。在试验中,先采用频域方法对本次试验中风压的信号在频域进行修正,再转换为时域信号进行后文的分析。
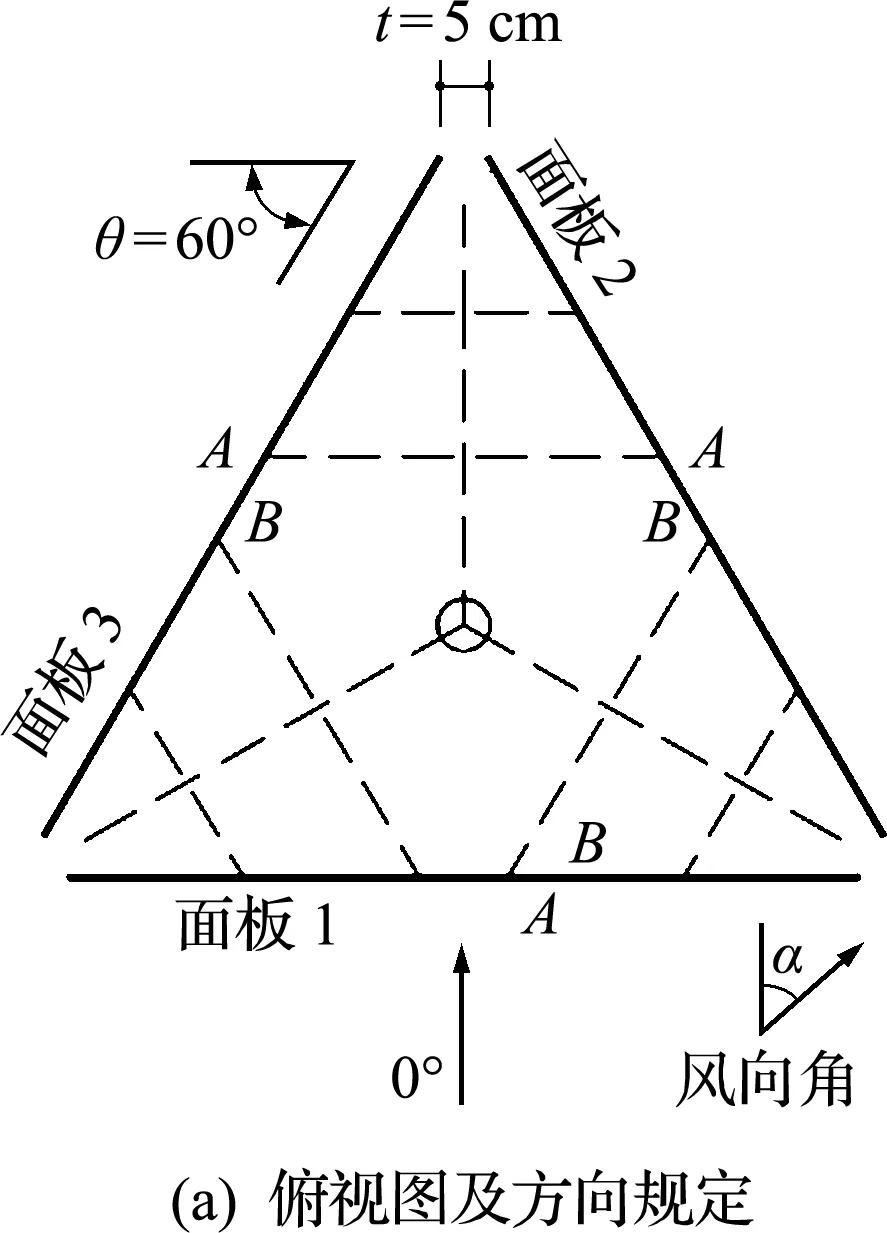
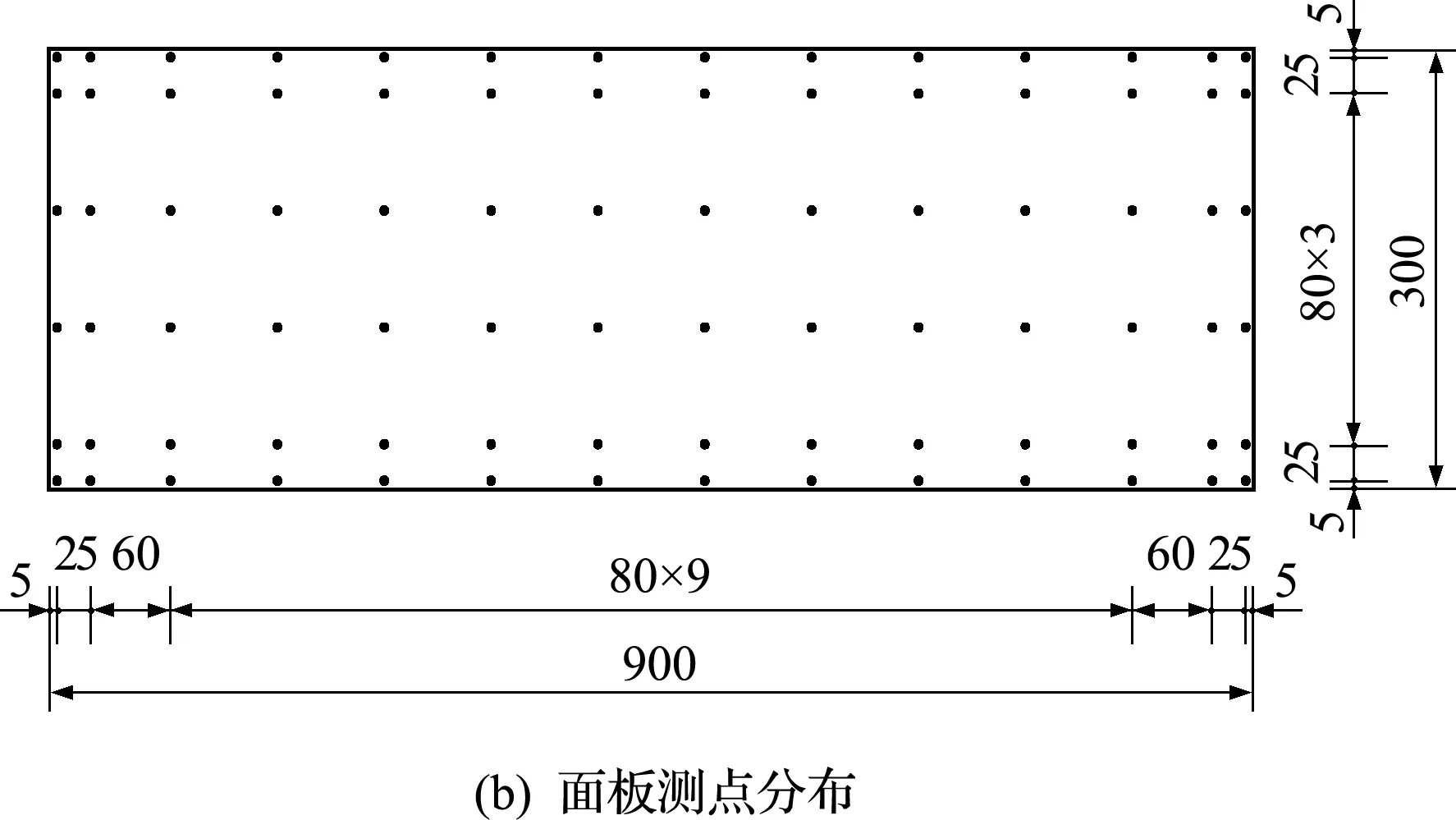
图1 模型主要参数
2.2 风场模拟
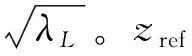
试验使用美国PSI扫描阀公司生产的DTCnet电子式压力扫描阀测压系统测量风压时程,采样频率332 Hz。实际工程应用中,风压的设计标准值往往取标准时长T=10 min。本次测压试验中,依据时间相似比,对应标准测试时长t0=135 s。在均匀流工况中采用t0;对B类和C类地貌的湍流风场工况,为获得足够的风压极值分布的信息,每个工况采样时长为3t0。试验中,风向角测试范围α=0°~60°,每15°一个测试工况。试验工况列入表2。
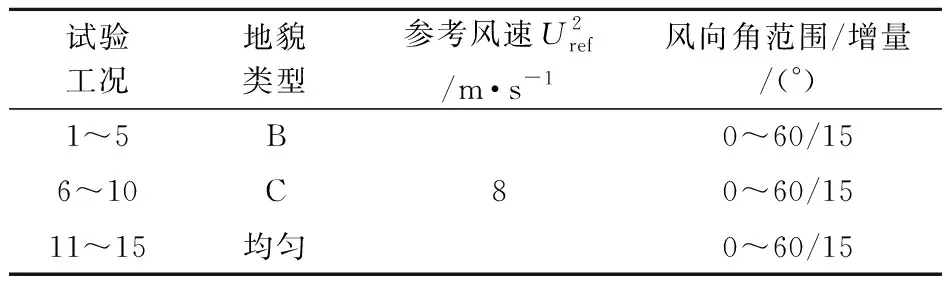
表2 三面广告牌刚性测压试验工况
3 数据处理方法
3.1 非高斯区域的划分方法
对于非高斯时程,均值和方差不足以完整地描述其概率特征,必须引入三阶中心矩(偏度skewness)及四阶中心矩(峰度kurtosis)统计量来表征,
当峰度大于3时可视为软化非高斯过程,当峰度小于3时可视为硬化非高斯过程。本文参考Kumar等[16]的研究结果,将偏度和峰度绝对值分别大于0.5和3.5的风压时程定为非高斯风压时程。当风场的湍流度增大,广告牌各面板上的非高斯性皆有一定增强。其中背风面面板三上非高斯性的增强十分明显。因此,后文将以面板三为例,研究其极值风压的分布情况。
3.2 风压时程统计最大值(样本统计法)
试验中首先同步采集到面板外侧A面风压时程PA j和内侧B面同一位置测点风压PB j的时程数据,通过式(3)叠加得到对应测点数据净风压Pi j,其中i为广告牌单个面板的编号,分别为1~3;j为i面板上采集点的编号,分别为1~84。
Pi j(α,t)=PA j(α,t)-PB j(α,t)
(1)
(2)
式中对时程Pi j取峰值得到极值风压Ppeak,i j,Ppeak,i j为与该点平均风压符号相同的最大风压。进而可依据式 (4)得到该测点的极值风压系数Cpeak,j i(α),式中ρ为空气密度。对于湍流风场工况,将3t0时长的风压时程分为30段,然后依次将相连的10段作为一个时长t0的样本,标记为样本k,采用式(4)可计算得到Cpeak,j i,k(α)。然后按照式(5)取均值作为本节方法(样本统计法)的极值风压系数CS,
(3)
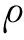
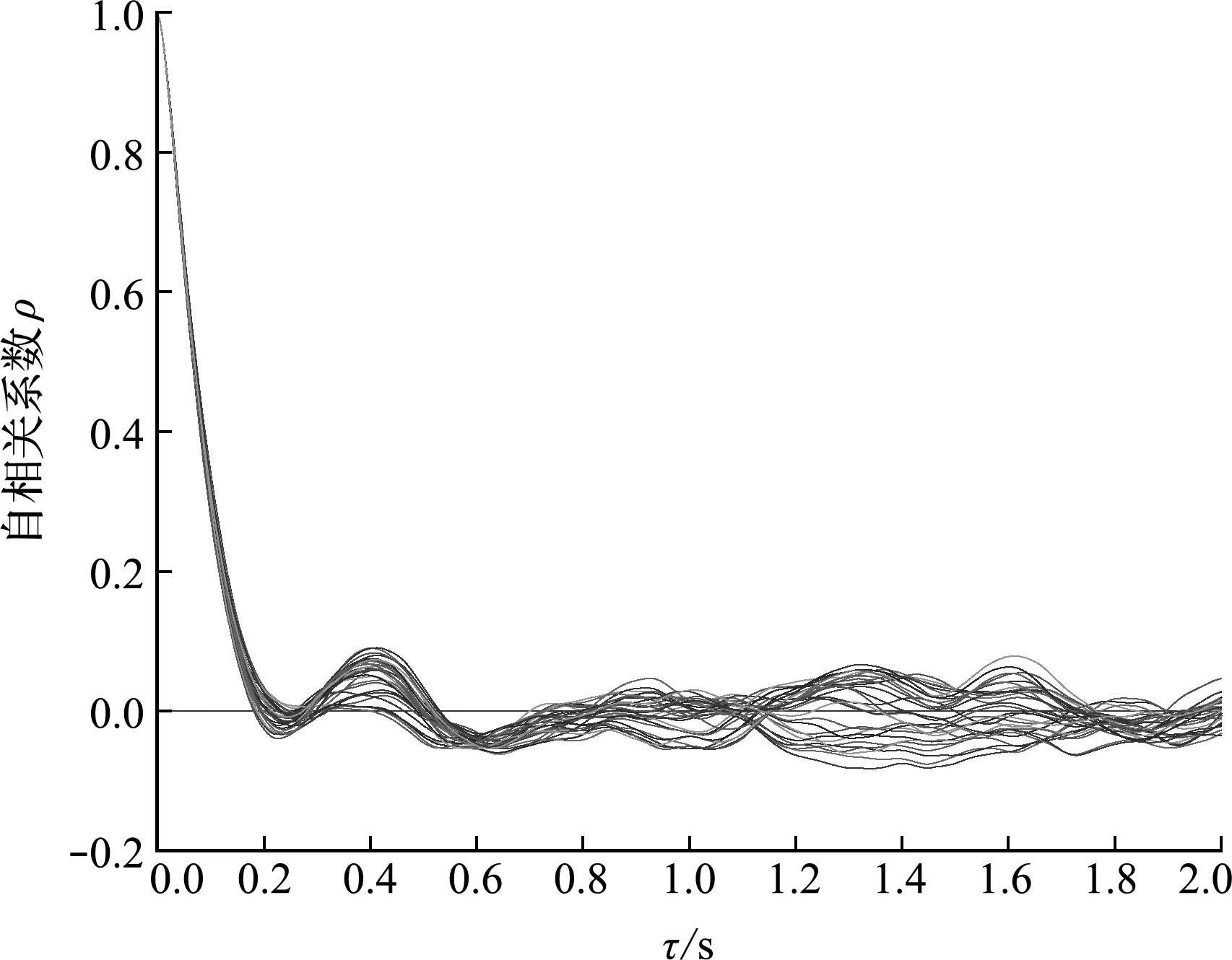
图2 风压时程自相关系数
3.3 基于Hermite四阶矩转换的极值计算方法
对于广告牌面板而言,其上风压时程几乎全部属于软化非高斯时程。故此处仅给出软化非高斯时程的计算方法,即将非高斯时程标准化,可得到均值为0和方差为1的标准非高斯过程X(t)。X(t) 可以通过一个单调转换函数与一个基本标准高斯过程U(t)产生联系,
(4)
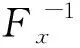
对于峰度α4处于3~15的过程,基于非高斯过程和Hermite模型,以偏度和峰度的差异最低为最优原则,给出了转换系数解析表达式为
(5)
(6)
(7)
h40={[1+1.25(α4-3)]1/3-1}/10
(8)
式中α3和α4分别为过程的偏度和峰度,κ和hn为模型系数。转化为标准高斯过程的平均0上穿越率v0可计算为
(9)
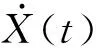
(10)
进一步,可计算出对应的软化非高斯过程U(t)的极值因子gN G为
gN G=κ[g+h3(g2-1)+h4(g3-3g)]
(11)
最终,Hermite计算的极值风压系数的期望值CH可以计算为
CH=Cmean+gN GCrms
(12)
式中Cmean和Crms分别为平均风压和脉动风压,其中脉动风压是风压系数时程的标准差。
3.4 最佳线性无偏估计方法(BLUE法)
最佳线性无偏估计BLUE(Best Linear Unbiased Estimation),是一种基于块极大值估计风压时程极值风压系数的方法,由Lieblein[19]提出。此方法较为突出的优点是只需要利用数据的一阶和二阶矩就可以进行估计,因此适用于实际工程。
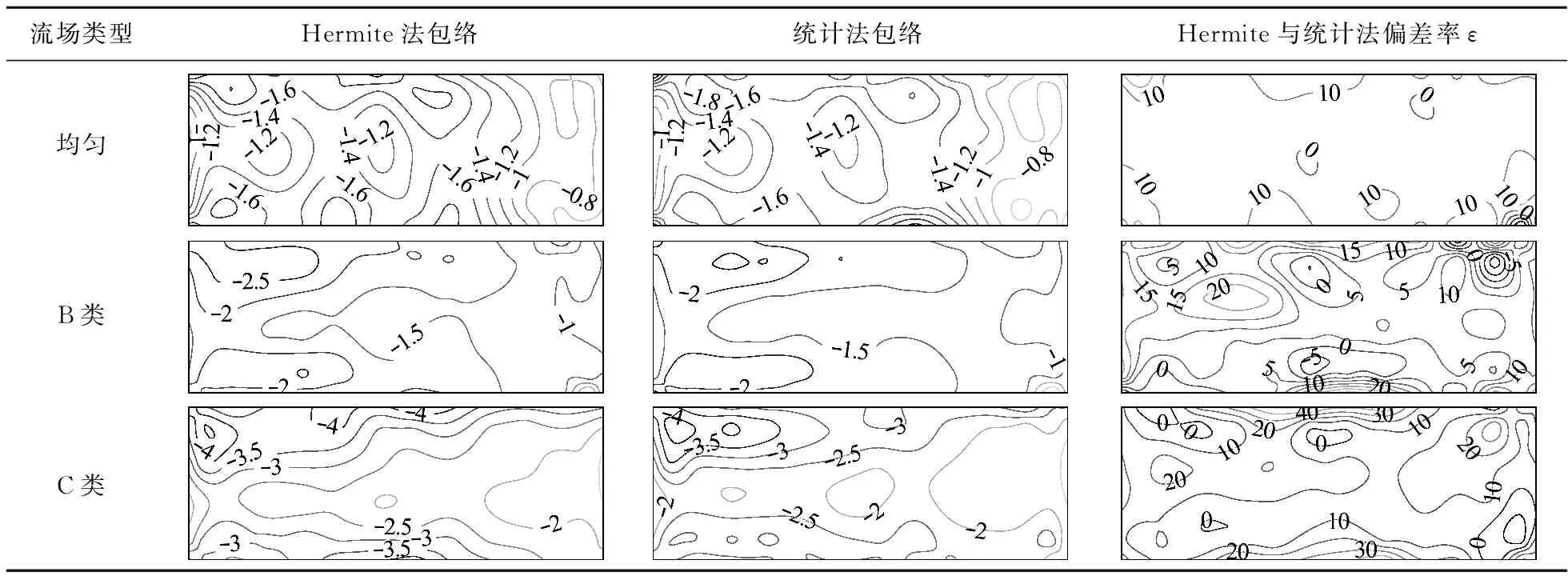
将整个时长的风压系数时程分成N个样本(N在4~100取值),本文为了保证计算的精度,在后文的所有极值风压系数分析中,均取N=100。依据式(4)提取每个风压系数时程样本的峰值,当样本的平均风压为正时,按升序排列(Cpeak,1 (13) (14) 式中Ai和Bi分别为加权系数(i=1,2,3,…,N),依据文献查表可得[19];λp=log(-log(p))根据极值I型分布中期望对应的保证概率p=57.04%计算得到λp=0.5772。n为用于估计极值时所取的样本数量,由于本文整个时长为3t0,所以计算标准时长t0对应的极值期望时,n=N/3。为了与前述方法区别,通过式(16)得到的极值期望采用CB=Cpeak,n表示。 对比上述的三种方法,其中统计法和BLUE法都是将样本分块,对这些块取峰值,然后通过一定的方法将这些峰值进行组合,是基于样本时程来统计极值。而Hermite法是基于样本的概率特征参数计算极值,与前两者有本质上的区别。 首先,选择紊流度较小的均匀流场、0°风向角和面板一,图3给出Hermite法与统计法计算结果的偏差率,偏差率ε定义为 ε=(CH-CS)/CS×100% 式中CH和CS分别为采用Hermite法和统计法计算得到的极值风压系数。 此时这两种方法的计算结果几乎没有区别,这说明使用Hermite法计算极值风压系数具备良好的精度。同时,为了研究风场湍流度提高对极值风压系数的影响规律,表3分别给出了均匀流场、B类流场和C类流场的极值风压等值线。 图3 偏差率ε等值线(单位:%) 从三种流场的横向对比可见,风场的湍流度越高,风压时程的非高斯性就越强,极值风压系数的均值亦有显著提高,说明风压时程的非高斯性强弱与极值风压系数的大小有明显的关系。同时,极值风压系数最大值出现在面板的边缘,而面板边缘的风压时程大多具有更显著的非高斯性。在同等风速下,风压时程的非高斯性越强,极值风压系数越大,也表明非高斯风压更容易使结构发生破坏。 由表4可知当风场为均匀流场时,两种计算方法的偏差率不大,在10%以下;而当风场为B类流场时,其之间的偏差率就增加至15%左右;当风场湍流度进一步增加时,二者的偏差趋向更大。最大处超过30%,使用基于Hermite四阶矩转换的风压极值计算方法得出的结果偏于安全。值得一提的是,偏差基本出现在面板边缘,面板中心位置的计算结果始终相似,这说明计算时没有出现错误。 此外,两种计算方法偏差的最大值往往出现在面板边缘,而这些位置风压时程的非高斯性也往往较强,这说明非高斯性越强的风压时程,越不适合简单取风压时程最大值为极值风压。并且,简单地依据时程取最大值的方法得到的极值风压系数往往偏小,使得抗风设计偏于危险。 表4 负压极值包络及偏差率ε(单位:%)Tab.4 Negative pressure extreme envelope diagram and deviation contour diagram ε (unit:%) 图4给出在风向角为0°时,均匀流场下面板一上BLUE法计算极值与统计法计算结果的偏差率。与图3相同,从图4可以看出两种方法计算的偏差率很小,与上文类似,这说明使用BLUE法计算极值风压系数具备良好的精度。表5给出了BLUE法计算的极值风压系数等值线。 图4 偏差率ε等值线(单位:%) 表5 面板三的极值风压系数的等值线(BLUE法)Tab.5 Equivalent line diagram of extreme wind pressure coefficient for panel 3 (BLUE method) 面板上极值风压系数随风向角和湍流度变化的规律和Hermite法基本一致,这两种截然不同的计算方法得出一致的结果也可以说明两种计算方法都适于计算广告牌面板的极值风压系数。 表6第一和第二列给出BLUE法与统计法的计算结果包络图进行对比。 表6 负压极值包络及偏差率ε(单位:%)Tab.6 Negative pressure extreme envelope diagram and deviation contour diagram ε (unit:%) 除面板上下边缘,这两种计算方法的计算结果没有明显的区别(5%左右)。但是在面板边缘处(非高斯性较强位置),BLUE法计算的极值风压系数明显小于统计法,而且随着湍流度上升,面板边缘处的偏差率越来越大,最大达到30%。这表明大部分情况下,时程的非高斯性越强,BLUE法的计算结果相对于统计法越小。同样,面板中心位置的计算结果始终相似,计算时没有出现错误。 表6第三列给出BLUE法与Hermite法计算结果包络图的差值(同样仅给出负压)。与表4中Hermite法与统计法的差值对比可以发现,BLUE法与Hermite法的差值在边缘位置的差值明显更大。但这两种差值随湍流度变化的规律大致相同,与表6观察到的现象吻合。 而在实际使用中,由于Hermite法使用了风压时程的三阶与四阶矩,BLUE法仅使用了一阶和二阶矩,统计法更是直接对时程进行处理,在方法的计算速度上有明显的区别,统计法与BLUE法的计算速度明显快于Hermite方法。 (1) 从三种流场的横向对比可见,风场的湍流度越高,风压时程的非高斯性越强,广告牌面板上极值风压系数的均值亦有显著提高,所以风压时程的非高斯性强弱与极值风压系数的大小有明显的关系。同时,广告牌面板上极值风压系数最大值出现在面板的边缘,而面板边缘的风压时程大多具有较强的非高斯性,这说明在同等风速下,非高斯性较强风压时程的极值风压系数更大,这也表明面板分离区的非高斯负风压更容易使结构发生破坏。 (2) 依据《建筑结构荷载规范(GB 50009-2012)》及《户外广告设施钢结构技术规程(CECS148-2003)》,本文试验对象的极值风压系数分别为2.1(B类地貌)和2.6(C类地貌)。然而,依据本文试验,背风面面板局部区域的负风压面板上极值风压已经分别为2.5(B类地貌)和3.5(C类地貌)。使面板连接及支撑结构抗风设计值偏小,易导致面板或面板支撑结构的风灾破坏。 (3) 在工况为均匀流场,0°风向角时,面板一上统计法、Hermite法和BLUE法的极值风压系数的计算结果几乎没有区别。但随着风场湍流度增加,风压时程的非高斯性增强,三者间的差别也变得更大。在处理非高斯时程时,极值风压系数的计算结果大小排序为Hermite法>统计法>BLUE法,而且随着非高斯性的增强,偏差率也随之增加。使用Hermite转化的理论方法的风压极值计算方法得出的结果偏于安全。 (4) 综合上述三种计算方法对非高斯风压极值的分析和比较,可依据不同情况选取合理的极值计算方法:由于BLUE法与Hermite转换法对风压时程的长度要求不高,当试验风压时程较短,风场的紊流度较小时,可采用BLUE方法;当试验风压时程较短,且紊流度较大时,可采用Hermite方法;若试验风压时程足够长,可采用直接统计法。4 分析对比
4.1 Hermite法与统计法
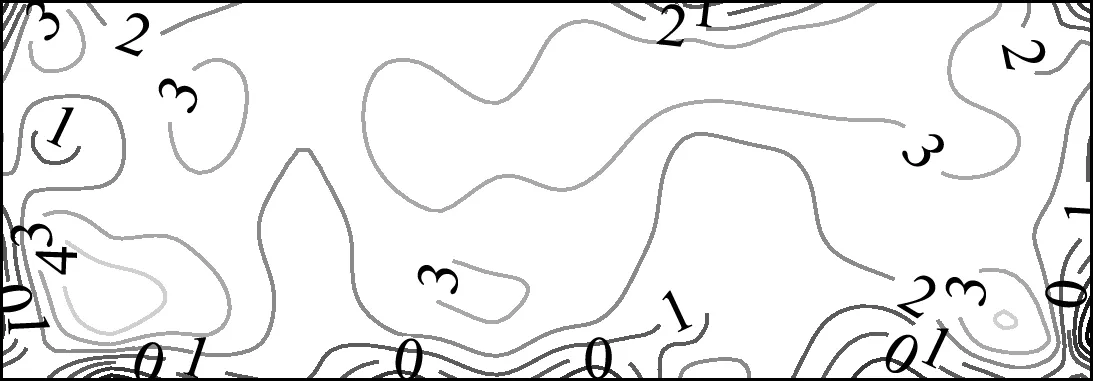
4.2 BLUE法与统计法
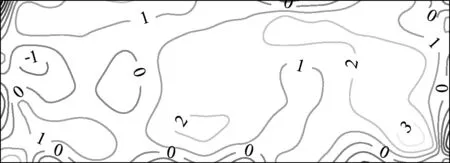
4.3 BLUE法与Hermite法
5 结 论
