拱桥悬臂施工过程中面内特征值的传递矩阵法
2022-04-20康厚军朱国敬苏潇阳
康厚军, 朱国敬, 苏潇阳
(1.湖南大学 土木工程学院,长沙 410082; 2.广西大学 土木建筑工程学院,南宁 530004)
1 引 言
拱桥是一种古老的桥梁结构,其两端除了产生竖向反力之外,还产生可以大大降低拱截面弯矩的水平反力。大多数拱桥施工采用斜拉悬臂浇筑法,考虑到斜拉索和拱桥主体结构的耦合振动,合拢过程中的振动状态尤其复杂。因此,围绕拱桥施工中的动力学行为,国内外学者在拱桥建模方面做了大量研究。
丁毅[1]考虑了竖转加平转施工的钢箱拱桥,通过将其竖转动态过程分解成不同角度的静力模型,借助正装迭代法求得索力,进一步分析了拱桥竖转施工过程的静动力和稳定性性能。孟繁义[2]建立台风区的东莞水道特大桥有限元三维模型,对其主拱吊装阶段的动力特性进行了计算分析,为该桥的顺利建成提供了科学数据。向中富等[3]实际研究了拱桥拱架施工过程中的结构行为分析方法与模型,并通过实桥分析、模型试验和实桥测试结果比较证明了其分析方法的可行性。訾银辉等[4]在斜拉悬臂浇筑施工拱桥正装计算中引入优化理论,采用一阶分析法进行迭代优化,有效改善了施工阶段拱圈截面的受力。康厚军等[5-7]基于索拱结构的力学模型,考虑拱结构的几何方程和物理方程,并根据索拱自由振动的动力学方程,利用半解析方法-传递矩阵法对索拱结构面内及面外自由振动特征值问题进行了求解。文献[8,9]均采用有限元程序 Midas 计算并探讨了钢管混凝土拱桥的静力特性、动力特性和施工过程以及成桥后的稳定性能,为钢管混凝土拱桥的设计和施工提供了参考。易壮鹏等[10]提出了多索支撑拱的全局分析模型,将整体分为多个部分,再将各个部分组装为整体,以模拟拱桥的斜拉索架设施工,并对平面内自由振动特性进行了结构参数研究。
多体系统传递矩阵法是一种采用矩阵来描述多输入多输出的系统内部输入与输出之间关系的手段和方法,近年广泛应用在桥梁体系动力学特性研究中。芮筱亭等[11,12]发展了多体系统传递矩阵法,研究了多体系统发射动力学理论与技术,并将其应用在火箭和火炮武器射击精度和安全性设计与试验研究中。谢维东[13]提出了上中下承式三种拱桥整桥面内自由振动特性的通用简化动力学模型(拱-弹簧-梁组合体系),并利用哈密顿原理推导出其面内自由振动的控制微分方程,结合传递矩阵法求解其特征值。苏潇阳等[14]建立了斜拉桥的多索梁模型,并考虑索和梁的轴向和横向振动的微分方程,基于传递矩阵法的基本原理对模型自由振动特征值进行求解,并与ANSYS得出的精确解进行对比,相对误差很小。康厚军等[15]建立了漂浮式独塔斜拉桥新的三梁离散弹簧整体动力学模型,并利用传递矩阵法结合相应的动力学理论关于其进行求解。文献[16,17]基于漂浮式独塔斜拉桥三梁离散弹簧动力学模型,采用传递矩阵法关于拉索对斜拉桥竖向振动频率的影响进行了研究,并介绍了采用传递矩阵法对不同体系斜拉桥的处理方法。吉伯海等[18]充分考虑了斜拉桥的延伸、塔的弯矩和轴力引起的位移及转角等因素,利用传递矩阵法并结合斜拉桥自身的特点确定了联立方程组所需的若干边界条件和兼容条件,从而实现斜拉桥内力和位移的求解,为大型桥梁结构初步设计提供了新型便捷的计算方法。刘利等[19]应用传递矩阵法对径向均布荷载作用下的圆拱面内屈曲微分方程进行解答,利用边界条件导出其特征方程,从而求得其屈曲荷载。
综上所述,现有的对索拱结构动力学的研究多为有限元方法,但是这种方法的精度依赖于建模方法以及单元划分规则,并且在模型参数发生变化时,有限元方法会因为重新建模而变得非常复杂[20],因此对于模型的参数分析效果稍显不足。传递矩阵法在机械、军工、航空航天和土木工程等领域虽有广泛应用,但用于拱桥施工过程中动力学分析的研究尚未见到。与此同时,拱桥在施工过程中,合拢前的最大悬臂状态和刚合拢的索-拱阶段为最危险的施工工况。鉴于此,本文基于拱桥的力学模型,考虑索拱结构的面内自由振动的动力学方程,并结合索拱耦合处的位移协调条件,将传递矩阵法应用在拱桥合拢过程的动力学分析中,对其面内特征值问题进行求解。同时,采用有限元软件建立了拱桥施工合拢时全跨和合拢前半跨的有限元模型,并将频率和振型与本文方法得到的结果进行对比,验证了本文方法的正确性,同时也建立了该类桥型施工过程中面内竖弯刚度的评估方法。
2 索拱模型
2.1 基本构型及假设
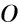
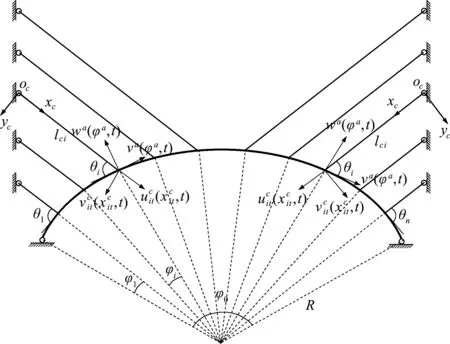
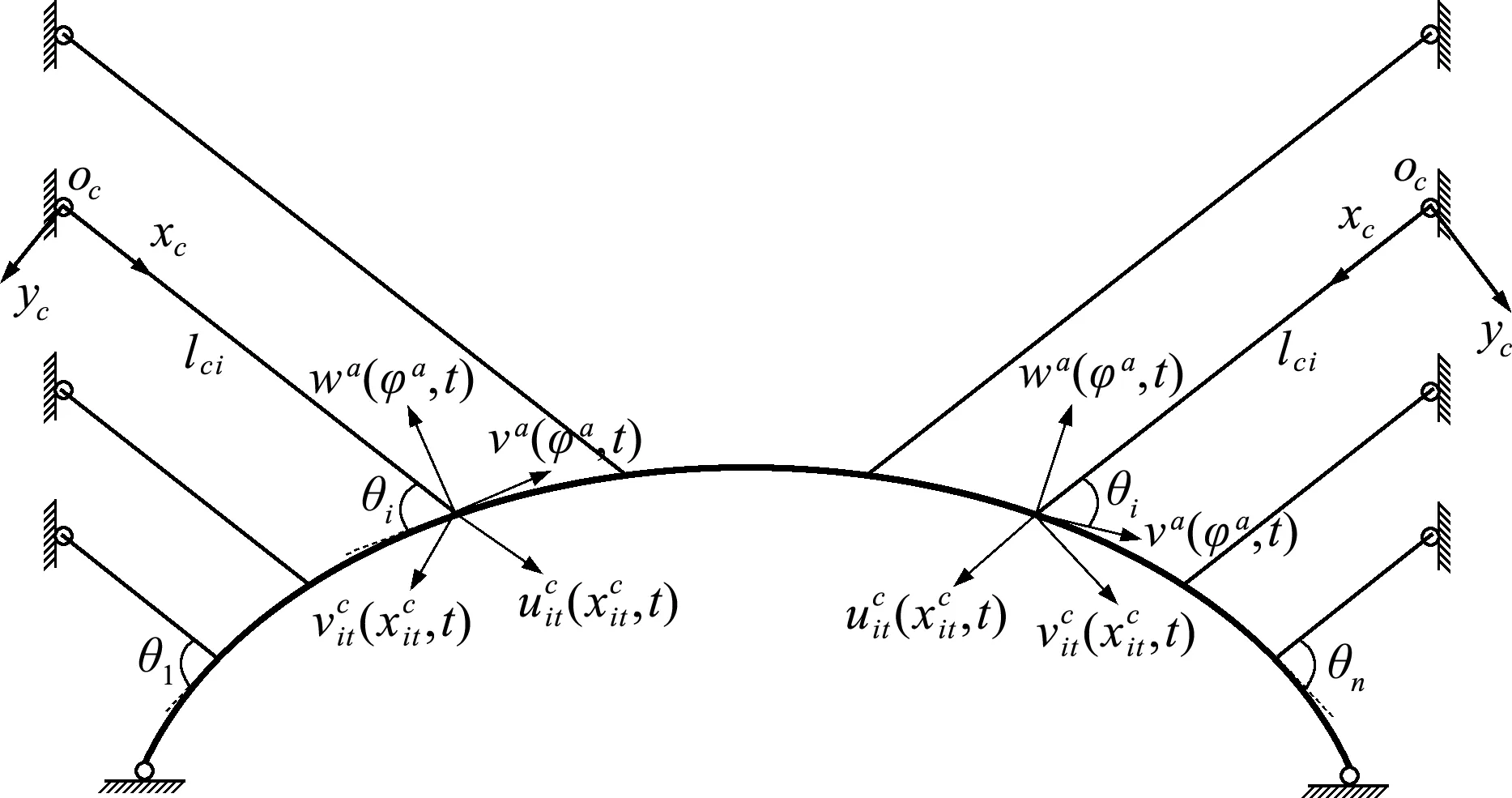
图1 拱桥合拢状态模型
(1) 为便于求解拱结构的微分方程,将拱局部坐标系设为极坐标系,坐标原点为圆心,拱的两个线位移分别为径向位移和切向位移。
(2) 不考虑拱剪切变形的影响,即按照欧拉-伯努利梁的振动方程求解。
(3) 索的垂度和初始静态构型忽略不计。
(4) 仅考虑索和拱的小幅振动,且拱轴线不伸缩。
2.2 传递矩阵求解
首先,考虑拱的平面内振动微分方程[5],
(1)
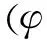
∂2v/∂t2=-ω2v
(2)
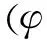
(3)
方程(3)对应的特征方程为
r5+2r3+(1-x2)r=0
(4)
解得特征方程(4)的根有
因此,方程(1)的解可以写成级数形式为
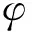
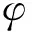
(5)
(6)
式中Cj(j=1,2,…,6)为实常数系数。
对x的大小分类讨论。
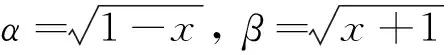
此时,根据力的平衡条件、内力与变形的物理关系,可得到切向位移u、径向位移v、相应于拱轴方向上的转角θ、弯矩M、剪力Q和轴向力N的表达式分别为
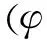
T15C5+T16C6
(7)
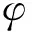
(8)
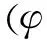
T35C5+T36C6
(9)
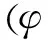
(10)
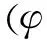
(11)
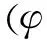
(12)
元素T11~T65见附录1。
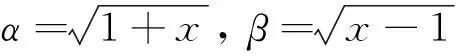
同样得到式(7~12),只是元素Ti j不同,见附录2。
其次考虑索的纵横向振动微分方程为
(13)
(14)
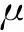
Uc(xc,t)=uc(xc)Gc u(t)
(15)
Vc(xc,t)=vc(xc)Gc v(t)
(16)
式中uc(xc)和vc(xc)分别为索的纵向和横向振动振型函数,通过求解偏微分方程(13,14)可以得到uc(xc)和vc(xc)通解形式为
uc(xc)=C7sin(βcxc)+C8cos(βcxc)
(17)
vc(xc)=C9sin(δcxc)+C10cos(δcxc)
(18)
式中Ci(i=7,…,10)为实常数系数,且
根据力-位移关系,由式(17,18)可以推导出轴力N和剪力Q的表达式为
Nc(xc)=C7EcAcβccos(βcxc)-C8EcAcβcsin(βcxc)
(19)
Qc(xc)=C9N0δccos(δcxc)-C10N0δcsin(δcxc)
(20)
2.3 传递矩阵法理论
将式(7~12)写成如下矩阵形式,
Za=TaCa
(21)
式中Za=[uavaθaMaQaNa]T,且
Ca=[C1C2C3C4C5C6]T
x<1或x>1时,Ta的元素T11~T65分别见附录1和附录2。
将式(17~20)写成矩阵形式为
Zc=TcCc
(22)
式中Zc=[ucvcNcQc]T,Cc=[C7C8C9C10]T,Tc元素T11~T44见附录3。
(23)
将式(23)代入式(21)可得
(24)
(25)
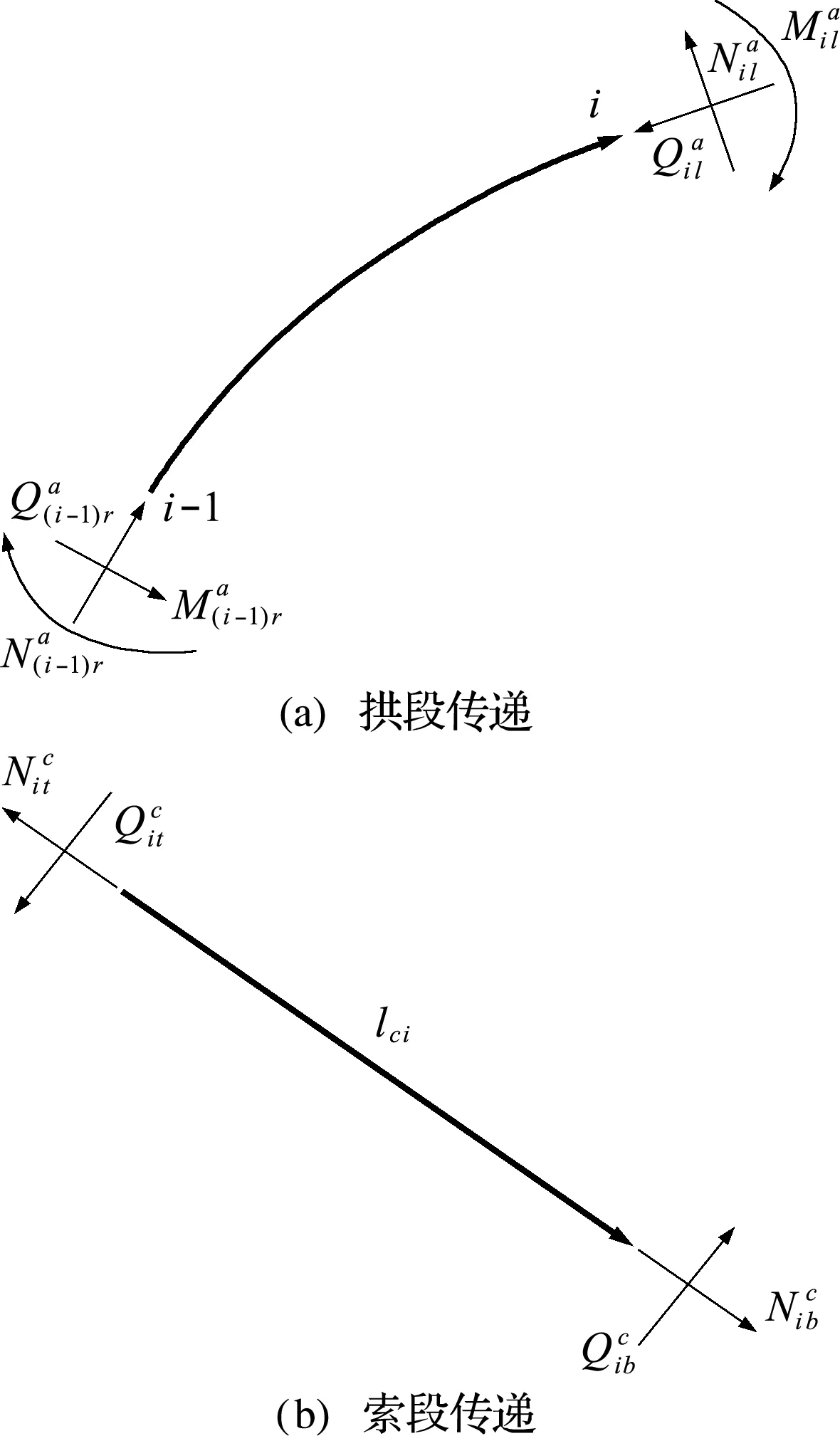
图2 拱段与索段传递
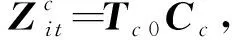
(26)
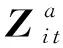
将式(26)代入式(22)可得
(27)
令式(27)的xc=lm,则有
(28)
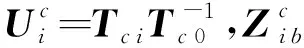
(29)
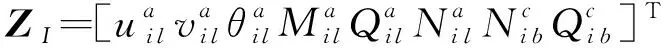
对拱左半部分m个索拱节点进行受力分析,如图3(a)所示,由受力分析和位移关系可得
(30)
将式(30)写成矩阵的形式,
(31)
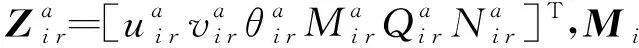
对拱右半部分n-m个索拱节点进行受力分析,如图3(b)所示,由受力分析和位移关系可得
(32)
将式(32)写成矩阵的形式,
(33)
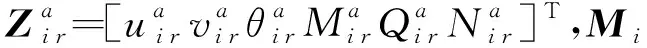
在拱节点i右侧,有传递方程
(34)
将式(25,28,29,31,33)代入式(34),可以得到整个体系的传递方程
(35)
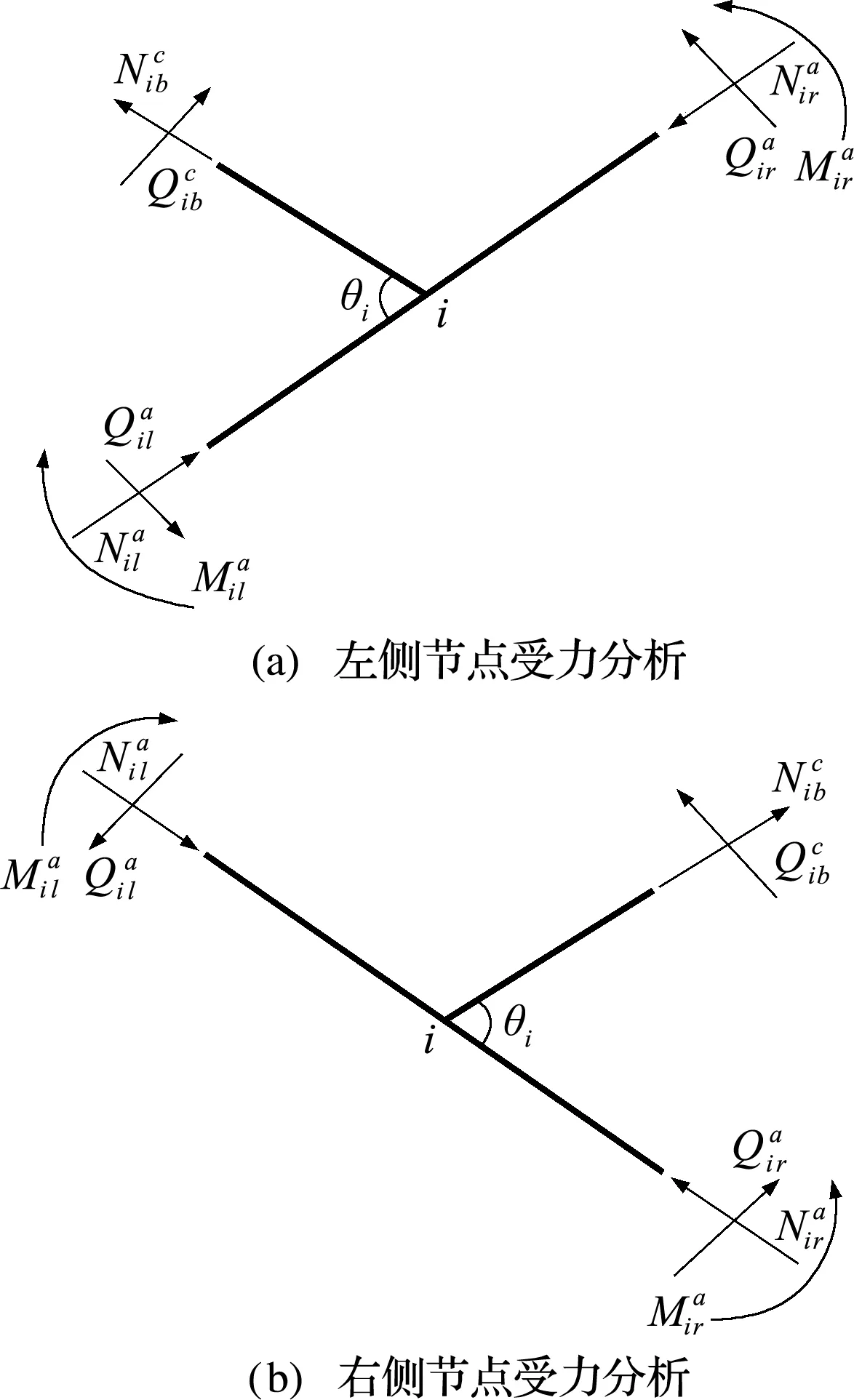
图3 节点受力分析
此外,考虑到索拱节点的位移协调条件,得到左侧m个节点的位移协调方程为
(36)
将式(36)写成矩阵形式,即
(37)


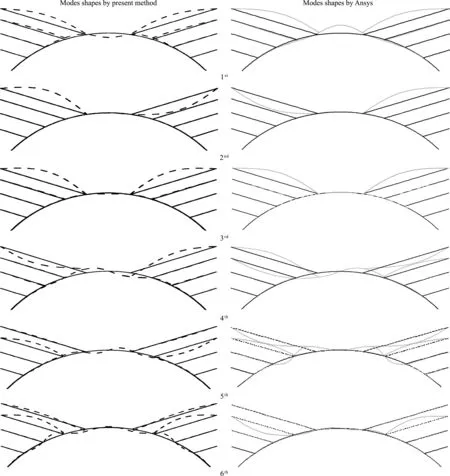
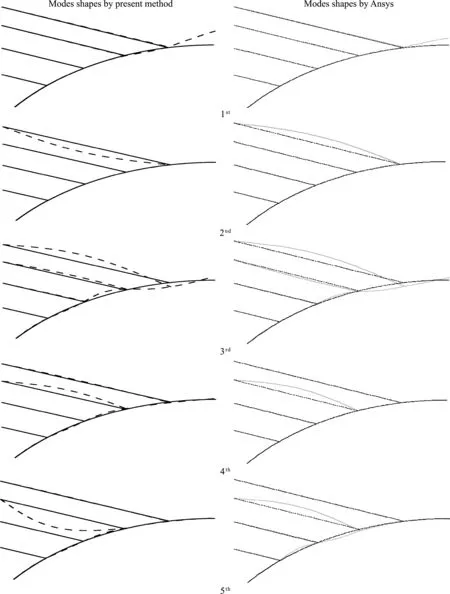
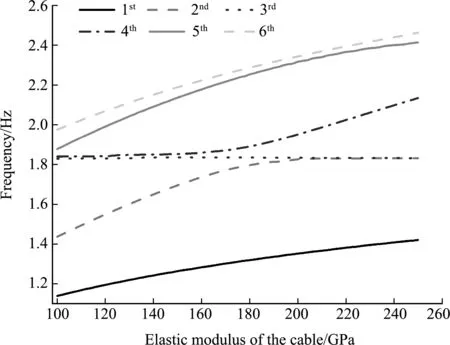
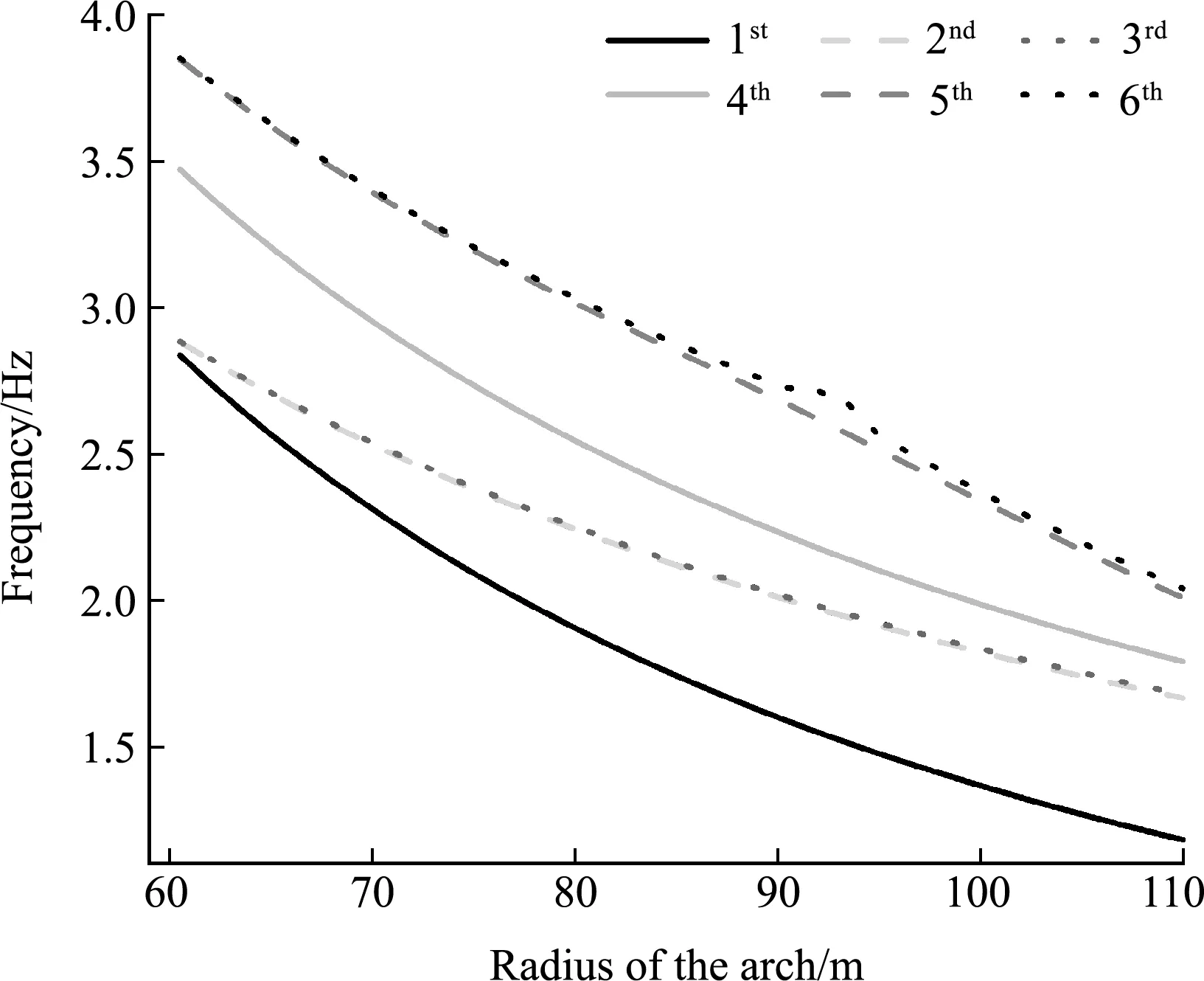
将式(25,28,29,31)代入式(37),得到在索拱结构左半部分m(m (i=2,3,4,…,m)(38) 右侧n-m个节点的位移协调方程为 (39) 将式(39)写成矩阵形式,即 (40) 将式(26,28,29,31,33)代入式(39),右半部分n-m(m (i=m+1,m+2,…,n)(41) 最后,联立式(35,38,41),可以得到整个系统的特征值方程 UallZall=0 (42) 式中Uall是整个系统的传递矩阵,Zall是索拱所有边界的总状态向量,含有4n+12个元素,即 (43) 若系统有非零解,必然有 (44) 式(44)即为系统的特征方程,利用数值分析软件MATLAB可以很容易得到其数值解。 以某拱桥合拢(图4)为例,对其面内特征值问题进行求解。拱桥和斜拉索参数如下,拱的半径为100 m,开角为100°,截面尺寸为0.3 m×0.8 m,单位长度质量为1872 kg/m,弹性模量Eb=3.45e10 Pa;斜拉索共8根,对称分布在拱的两侧,弹性模量Ec=2.1e11 Pa,面积均为A=0.005 m2,初始索力均为N=656250 N,索的作用位置为10°,20°,30°和40°,而索与作用点切线方向的夹角分别为60°,50°,40°和30°,索的锚固点与拱端点水平距离5 m。 图4 某拱桥合拢状态模型 为了验证本文理论的正确性,采用有限元软件ANSYS15.0 建立相应的索拱模型,拱采用Beam3单元模拟,索采用Link1单元模拟,共划分为510个单元。表1列出了本文理论和有限元模拟得到的结构前十阶频率。可以看出,本文理论计算得到的频率和有限元模拟得到的频率相对误差均未超过4%,最大误差仅第十阶的3.99%。图5给出上述两种方法计算得出的系统前六阶模态。可以看出,本文理论的前四阶模态和有限元模拟的结果一致,而第五阶和第六阶模态与有限元的结果刚好相反,原因可能是第五阶和第六阶频率比较接近,从而出现了振型互换的现象,但对模态影响不大。从图5和表1可以看出,两种方法得出的频率和振型相互吻合,说明本文的理论方法和建立模型的正确性,可以用在同类型拱桥合拢过程的基本动力学特性分析中。 表1 大跨拱桥合拢状态模型的前10阶频率Tab.1 The first 10 frequencies of the long -span arch bridge closed state model 图5 大跨拱桥合拢状态模型前六阶振型 为了进一步说明传递矩阵法解决此类桥梁合拢过程中动力学问题的适用性,本文采用上述理论和方法对拱桥合拢前的半跨模型进行了面内特征值求解。表2给出了拱桥合拢前半跨模型的本文理论和有限元模型的前十阶频率,可以看出,半跨模型自振频率的计算结果与有限元模型的结果相对误差较小,涉及拱的全局模态误差稍大,但总体吻合良好。图6给出了上述两种方法计算得出的前五阶模态,可以看出本文理论的前五阶模态和有限元模拟的前五阶模态也相互吻合,进一步说明了本文理论和方法的正确性。 表2 拱桥合拢前模型的前10阶频率Tab.2 The first 10 frequencies of the model before the closure of the arch bridge 图6 拱桥合拢前模型的前五阶模态 图7给出了模型前六阶频率随着拉索弹性模量变化的影响曲线。考虑到实际施工时不同扣索材料的选取,拉索的弹性模量变化范围从100 GPa增加到250 GPa,可以看出随着索弹性模量的增加,系统前六阶频率呈现增长的趋势,原因在于提高拉索的弹性模量会增大索对拱的支撑,提高了对拱的约束,从而增加了系统的自振频率。此外,图中相邻两阶频率之间出现了相互靠近又相互分离的现象,即结构中普遍存在Veering现象。此时两阶模态的频率十分接近,可能在一些情况产生1∶1 内共振并发生振型的互换。 图7 索的弹性模量对模型前六阶频率的影响 图9给出了模型前六阶频率随着拉索的初始索力变化的影响曲线。拉索的初始索力变化范围从0.65 MN增加到1 MN,可以看出模型的前六阶频率随着初始索力的增大而增大,这是因为增加索力会造成系统的几何刚度增大,从而系统的自振频率也会增大。此外,与图7类似,图9也出现了Veering现象,说明索拱结构很容易出现相邻两阶频率产生 1∶1 内共振并发生振型互换的现象,工程中应注意初始索力的选取,以避免Veering现象的发生。 图8 拱桥半径对模型前六阶频率的影响 图9 初始索力对模型前六阶频率的影响 本文基于拱桥的力学模型,考虑索拱结构的面内自由振动的动力学方程,并结合索拱耦合处的位移协调条件,将传递矩阵法应用在拱桥合拢过程的动力学分析中,并对其合拢状态前后的自振频率进行特征值求解,建立了该类桥型施工过程中面内竖弯刚度的评估方法。以某拱桥合拢模型为例,对其面内特征值问题进行了求解,并采用有限元模拟对本文理论得到的频率和模态进行验证,结果吻合较好。同时,针对前六阶频率进行了详细的参数分析,得到以下结论: (1) 本文理论和方法计算得出的拱桥合拢时全跨模型和合拢前半跨模型的频率和振型都与ANSYS有限元模型的计算结果一致,说明了本文理论和方法的正确性,可以应用在同类型结构的动力学分析。 (2) 增加拉索的弹性模量,增大了拉索对拱的支撑,提高了对拱的约束,因此会增大结构的前六阶频率。此外,各相邻阶频率之间出现了Veering现象,工程中应选取合适的拉索材料以避免内共振现象的发生。 (3) 增大拉索的初始索力,会增大系统的几何刚度,从而增大系统的自振频率。随着初始索力的增加,相邻各阶频率之间也会发生Veering现象,工程中应选取合适的拉索初始索力进行施工。 (4) 增加拱桥的半径,会减小结构的前六阶频率。当拱桥的半径增加时,使得结构的等效长度增加,减小了结构的等效刚度,从而对结构的自振频率起到了减小的作用。 T11=sin(βcxc),T12=cos(βcxc),T23=sin(δcxc) T44=-N0δcsin(δcxc),T32=-EcAcβcsin(βcxc) T43=N0δccos(δcxc),T31=EcAcβccos(βcxc) T24=cos(δcxc)

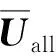
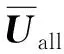
3 算例分析
3.1 模态分析


3.2 参数分析

4 结 论
附录1:
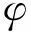
附录2:
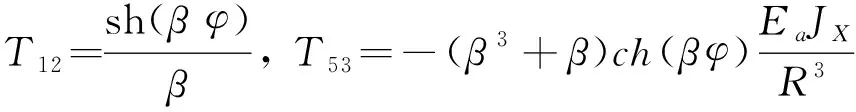
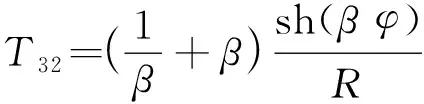
附录3:
