环境温度影响下基于支持向量机与强化飞蛾扑火优化算法的结构稀疏损伤识别

雷勇志， 黄民水， 顾箭峰*， 杨雨厚， 舒国明

(1.武汉工程大学 土木工程与建筑学院，武汉 430074；2.广西交科集团有限公司，南宁 530007； 3.河北交通职业技术学院，路桥工程系，石家庄 050035)

1 引 言

环境温度变化会对结构损伤识别造成较大的误差，这种变化引起的结构模态参数的波动甚至会掩盖因真实损伤造成的变化[1]。如何量化分析环境温度变化成为了该领域研究的重点与难点。在实际情况中，结构损伤常出现在受力关键部位，其位置分布呈稀疏性，但由于无法测得结构全部自由度上的模态信息，故识别损伤时常出现欠定方程组，而稀疏正则化技术能解决这一问题，从而提高识别精度[2,3]。此外，智能算法能够解决损伤识别中重复迭代问题，但常见的如遗传算法[4]及布谷鸟算法[5]等极易陷入局部最优，其收敛速度较慢，计算效率低下，需进一步改进提高其性能。

本文通过结合结构材料的温度-弹性模量变化关系，提出考虑温度变化的损伤识别模型，用于量化分析温度变化对损伤识别的影响，同时考虑实际结构中损伤的稀疏性，结合稀疏正则化技术得到稀疏损伤识别理论，随后立足于支持向量回归机与改进飞蛾扑火优化算法，提出一种环境温度影响下的结构稀疏损伤识别方法。为验证所提出方法的有效性，引入一温度影响下的简支梁结构与I-40钢-混组合体系桥梁进行温度预测及损伤识别工作。结果显示，该方法能够对结构环境温度的变化进行量化分析，同时也能对损伤进行准确的定位与识别。

2 考虑温度变化的损伤识别模型

结构内部损伤常在忽略质量变化的情况下简化为部件刚度线性折减，其数学模型可表示为

(1)

式中Kd为结构处于损伤状态下的整体刚度矩阵，Ke与θe分别为结构第e个单元的单元刚度矩阵及刚度折减因子，nele表示结构的单元总数。但结构在实际运营条件下，常受到环境温度变化影响，对于温度这一非线性影响因素，可将其转化为结构材料弹性模量的变化。图1为常见材料弹性模量随温度变化的曲线关系[6]。

综上所述，为考虑环境温度影响，获得考虑环境温度变化的损伤识别模型，式(1)可进一步写为

(2)

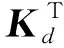
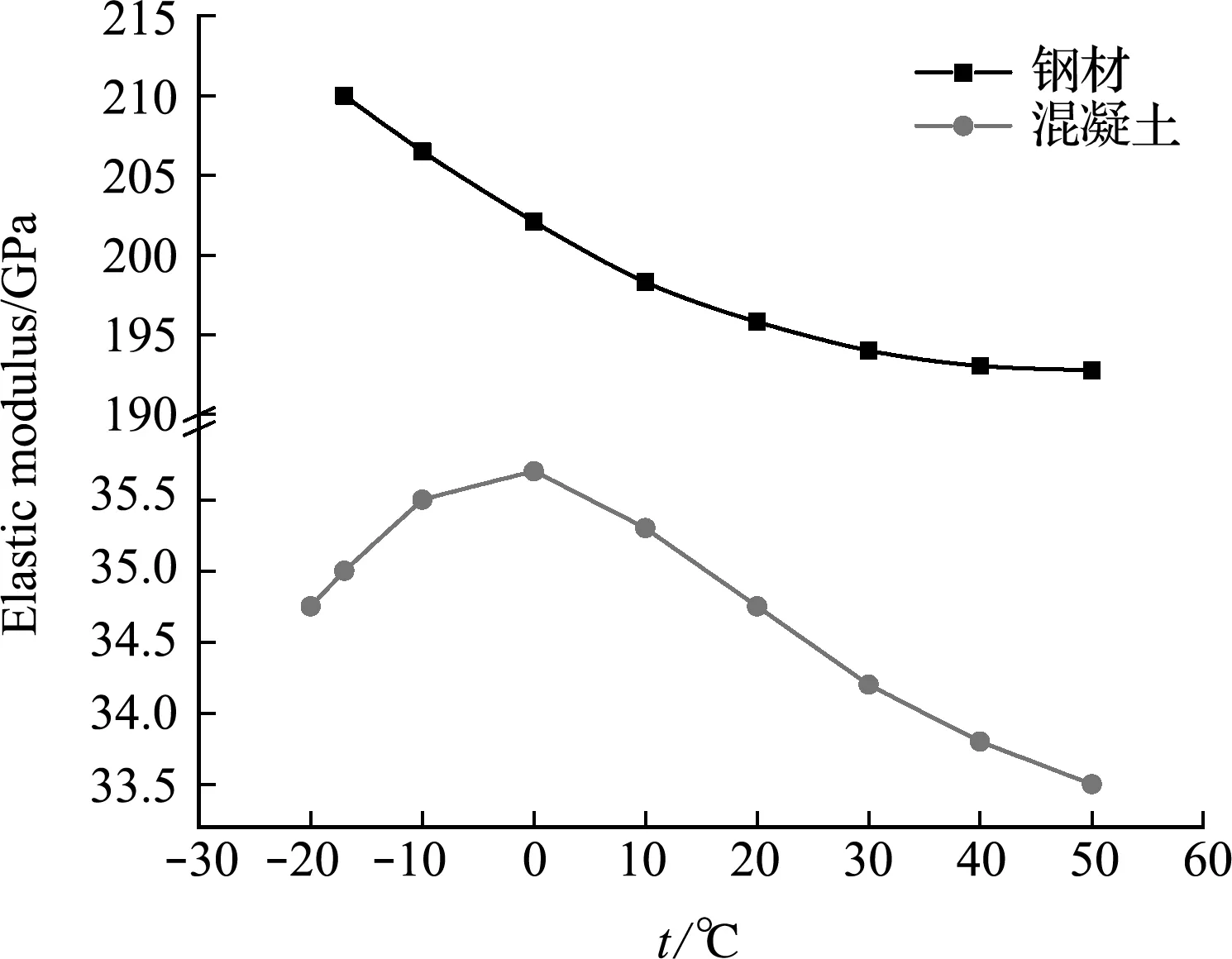
图1 常见材料弹性模量与温度变化关系

2 稀疏损伤识别理论

2.1 稀疏正则化理论

对于未观测的稀疏信号x=(x1,…,xa)∈Ra、观测值y=(y1,…,yb)∈Rc及设计矩阵A∈Ra ×c，有

Ax=y

(3)

对于上述方程组，常假设A为满秩，从而求得x，因此，对于任意y∈Rc，上述方程组存在解。当x的维度大于y的维度，即a≥c时，该方程欠定，为便于求解可对其添加正则化项，则式(3)可写为

(4)

式中ε为误差。式(4)可转化为无约束最小化问题，

(5)

式中μ为大于0的正则化参数，可采用l曲线法或AIC准则获得。正则化参数在于平衡正则化项及残差项，若μ值太大则导致欠拟合，反之为过拟合。

2.2 稀疏损伤识别

据灵敏度分析法，结构动力响应关于结构单元刚度折减因子的灵敏度矩阵可表示为

(6)

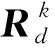
(7)

由于实测结构模态参数的阶数远小于结构的自由度数，故式(7)为一欠定方程组，然而，结构损伤的分布存在稀疏性，即损伤常出现在结构承载受力的关键位置，则θ为一稀疏向量，式(7)可写为

(8)

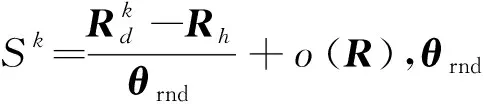
(9)

式中p为结构灵敏度矩阵S的基的数量,σ表示噪声干扰程度。在采用正则化理论求解欠定方程组时，易出现微小误差，对此，引入误差分布阈值法，以获得更加准确的损伤识别结果[9],

T=ER([s×(α/α*)×nm])

(10)

式中n为θ的维度；误差函数ER从大到小排列，α为nm个ER值的和；α*是最大ER值(即ER(1))与维度n的乘积；s为计算控制因子；[]表示取整。此处ER()定义为求得的刚度折减向量，其主要功能在于从刚度折减向量中挑选出少数真实损伤(或近似值)并消除微小误差，经挑选后的少数真实损伤(或近似值)构成向量T，该参数可大致反应结构损伤情况并指导下一步的损伤精准识别。计算控制因子s为对计算误差的容许程度，其值越大，容许程度越低，该参数可通过稀疏正则化求解欠定方程的精度ξ确定，其计算公式为

(11)

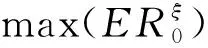
3 支持向量机与强化飞蛾扑火优化算法

3.1 支持向量机

支持向量机SVM(Support Vector Machine)属于监督学习方式的数据二元分类广义线性器[10]。Cuong-Le等[11]结合采用粒子群算法改进SVM，改进了SVM的损伤识别能力，并能实现较小损伤的量化识别。设高维空间中存在数量为n的训练样本点，可分为A与B两个数据类别，xi∈A时记yi=1，否则yi=0。假设存在一超平面可将两类样本点分隔，该超平面可写为

(i=1,2,…,n)(12)

(13)

式中C为惩罚系数，ε为误差精度。采用拉格朗日对偶定律，则回归函数可写为

(14)

3.2 强化飞蛾扑火优化算法

3.2.1 飞蛾扑火优化算法基本理论

飞蛾扑火优化算法[12]MFO(Moth-Flame Optimization)是一种新颖的群智能优化算法。文献[12]采用模态置信柔度与自振频率结合MFO算法，对桁架结构与40层剪力框架数值算例损伤进行了识别。基于H维解空间中，存在种群数量为np的飞蛾M=(M1,M2,…,Mn p)，对于群体的第l只飞蛾构成一个H维向量Ml，

Ml=(ml 1,ml 2,…，ml j)

(l=1,2,…,np;j=1,2,…,H)

(15)

则对应于第l只飞蛾存在环绕火焰Fl，

Fl=(Fl 1,Fl 2,…，Fl j)

(l=1,2,…,np;j=1,2,…,H)

(16)

引入OM与OF两个向量分别用于存放飞蛾个体及环绕火焰的适应度值,

(17)

(18)

式中ml j与Fl j分别代表第l只飞蛾与第l个火焰的第j个变量，it代表当前迭代，OMl与OFl分别为第l只飞蛾与第l个火焰对应的适应度值。迭代中，个体位置通过对数螺旋函数进行更新：

S(Ml,Fj)=Dl·eu t·cos(2πt)+Fj

(19)

式中Dl=|Fj-Ml|表示第l个飞蛾与第j个火焰之间的空间距离；u定义为对数螺旋函数的螺旋形状；t∈[-1,1]为随机数。引入自适应火焰递减强化算法的开发能力，其对应的公式为

(20)

式中Fni t与Fnmax分别代表第it次迭代时火焰数及最大火焰数；Iteration表示当前迭代数；Iterationmax表示最大迭代数；round()表示取整。

3.2.2 强化飞蛾扑火优化算法

MFO由于在迭代后期时种群多样性无法保证，故引入自适应个体更新机制、随机消除策略及自适应跳跃操作对其改进，提出强化飞蛾扑火优化算法EMFO(Enhanced Moth-Flame Optimization)。相关强化措施可总结如下，(1) 计算每个飞蛾距离当前全局最优个体的欧式距离，随后计算当前迭代飞蛾个体距离全局最优个体的平均欧式距离，

(21)

(22)

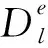
(23)

式中N(μ,σ)表示期望μ=(pbest+gbest)/2，方差σ=|gbest-pbest|的高斯随机数；gbest 与pbest 分别为全局与当前最优个体。否则对该个体实施随机消除策略以避免局部最优，相关公式如下,

(24)

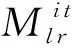
(25)

(26)

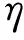
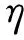
(27)

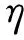
(28)

式中α=0.1，β=0.01[13]；ub与lb分别代表上下界。

3.2.3 EMFO优化性能评估

引入三个复杂测试函数对EMFO算法进行评估，并采用粒子群算法PSO(Particle Swarm Optimization)、布谷鸟算法CS(Cuckoo Search)及MFO算法进行对比。相关参数设定分别为，EMFO中随机消除概率为0.25[14]；PSO中加速度因子均为2，最大和最小惯性权重分别为0.9与0.4；CS中鸟巢发现概率为0.25。四种算法初始种群数量均设为100，迭代次数为500次。每种算法运行7次，取7次运行最优解及平均最优解。计算结果为，(1) 对于f1(x)，其最优解分别为7.424e -06(EMFO)，115.458(MFO)，16.932(PSO)，96.052(CS)；平均最优解分别为0.006(EMFO)，160.941(MFO)，21.924(PSO)，108.419(CS),

(xd∈[-5.12,5.12])(29)

(xd∈[-1.28,1.28])(30)

(xd∈[-10,10])(31)

(2) 对于f2(x)，其最优解分别为9.576e -05(EMFO)，0.002(MFO)，0.001(PSO)，0.005(CS)；平均最优解分别为0.001(EMFO)，0.004(MFO)，0.002(PSO)，0.009(CS)； (3) 对于f3(x)，其最优解分别为0.0002(EMFO)，10.401(MFO)，0.259(PSO)，27.087(CS)；平均最优解分别为0.0006(EMFO)，23.04(MFO)，0.490(PSO)，33.606(CS)。以上结果表明，EMFO可避免陷入局部最优。相对其他算法而言，具有更强的寻优能力及更快的收敛效率。

4 环境温度影响基于支持向量机与强化飞蛾扑火优化算法的结构稀疏损伤识别方法

4.1 目标函数

采用基于频率的结构多损伤定位保证准则MDLAC(Multiple damage location assurance criterion)[15]及模态应变能基本因子MSEBI(modal strain energy based index)[16]组建目标函数。基于频率的MDLAC指标定义如下,

(32)

式中ΔF=(Fh-Fd)/Fh，Fh与Fd分别代表结构损伤前后自振频率向量；δF(θ)=(Fh-F(θ))/Fh，F(θ)表示损伤向量为θ=[θ1,θ2,…,θnele]时结构自振频率向量。MSEBI计算公式为

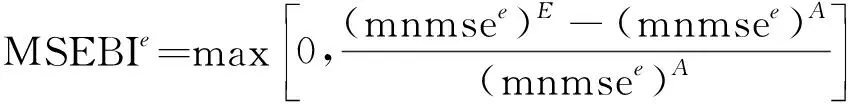
(e=1,2,…,nele)(33)

式中mnmsee代表nm阶标准化后的结构单元模态应变能取平均，其计算公式见文献[16]；max[]表示取最大值，上标E与A分别代表实际测试与理论分析。综上所述，在该过程中算法寻优的目标函数为

(34)

式中θ为结构刚度折减向量；T代表环境温度。

4.2 损伤识别方法

本文提出的环境温度影响基于SVR-EMFO的结构稀疏损伤识别方法，其主要步骤如下,(1) 建立有限元模型，随机生成稀疏损伤工况及环境温度，并将其作为输入数据引入有限元模型，得到自振频率数据； (2) 将得到的自振频率数据作为输入，对应的温度数据作为标签，输入SVR，以70%的样本为训练集，使得SVR进行充分的训练，并以30%样本为测试集，待测试样本的识别准确率达到90%认为该SVR已训练完毕； (3) 将试验测试得到的实际频率输入训练完毕的SVR进行温度预测，输出预测的环境温度；采用稀疏正则化求解刚度折减向量用于确定大致损伤工况； (4) 据SVR输出的温度与确定的大致损伤工况，作为EMFO的初始种群生成依据，产生具有针对性的种群； (5) 通过EMFO算法结合前文提到的目标函数识别损伤。

在实际应用中，可考虑对无损结构的自振频率及振型信息进行多次测量，并记录测量时的环境温度，构建训练集与测试集，经训练得到完备的SVR。待结构经服役后可能出现损伤时，再次对结构模态参数进行测量，导入SVR确定环境温度，同时基于正则化理论与灵敏度分析，确定可能的损伤工况；最后将预测的环境温度与可能的损伤工况结合EMFO算法和基准有限元模型，以实现环境温度影响下的结构损伤精准识别。

5 损伤识别算例

5.1 简支梁数值算例

通过Matlab建立如图2所示有限元模型。对于简支梁模型，其跨度为8 m，宽为0.3 m，高为0.1 m，弹性模量为3.45×1010Pa，密度为2500 kg/m3。以单元弹模折减模拟损伤，设置三种损伤工况，即单点(3#单元，损伤10%)、两点(3#和7#单元，分别损伤10%和5%)及多点(3#，7#和13#单元，损伤10%，5%和10%)，并考虑温度升高20 ℃(参考温度0 ℃)与不同噪声干扰，噪声添加公式为[13]

(35)

图2 简支梁模型

采用本文提出的方法对以上结构进行损伤识别， SVR中相关参数设定为惩罚系数C=1000，方差g=0.15,误差精度ε=0.15，训练样本数为1000。EMFO算法的种群大小为100，最大迭代1000次，正则化求解精度ξ=10-5。针对每种工况运行7次，取平均结果。识别结果如表1与图3所示。

由表1温度识别结果可知,(1) 无噪声下，温度识别十分准确，其误差均处于0.05 ℃以内； (2) 噪声影响下，温度识别能力有所下降，当噪声程度为1%时，其最大误差为0.061 ℃，当噪声程度为2%与3%时，最大误差分别为0.271 ℃与0.303 ℃。

从图3损伤识别结果可知,(1)在环境温度变化与噪声的双重影响下，本文提出的方法针对单点、两点及多点损伤工况均能实现准确的定位； (2) 在损伤量化方面，单点工况最大误差为 0.305%，两点及三点工况的最大误差分别为 0.569% 与0.56%，同时噪声干扰在一定程度上会增大误差。

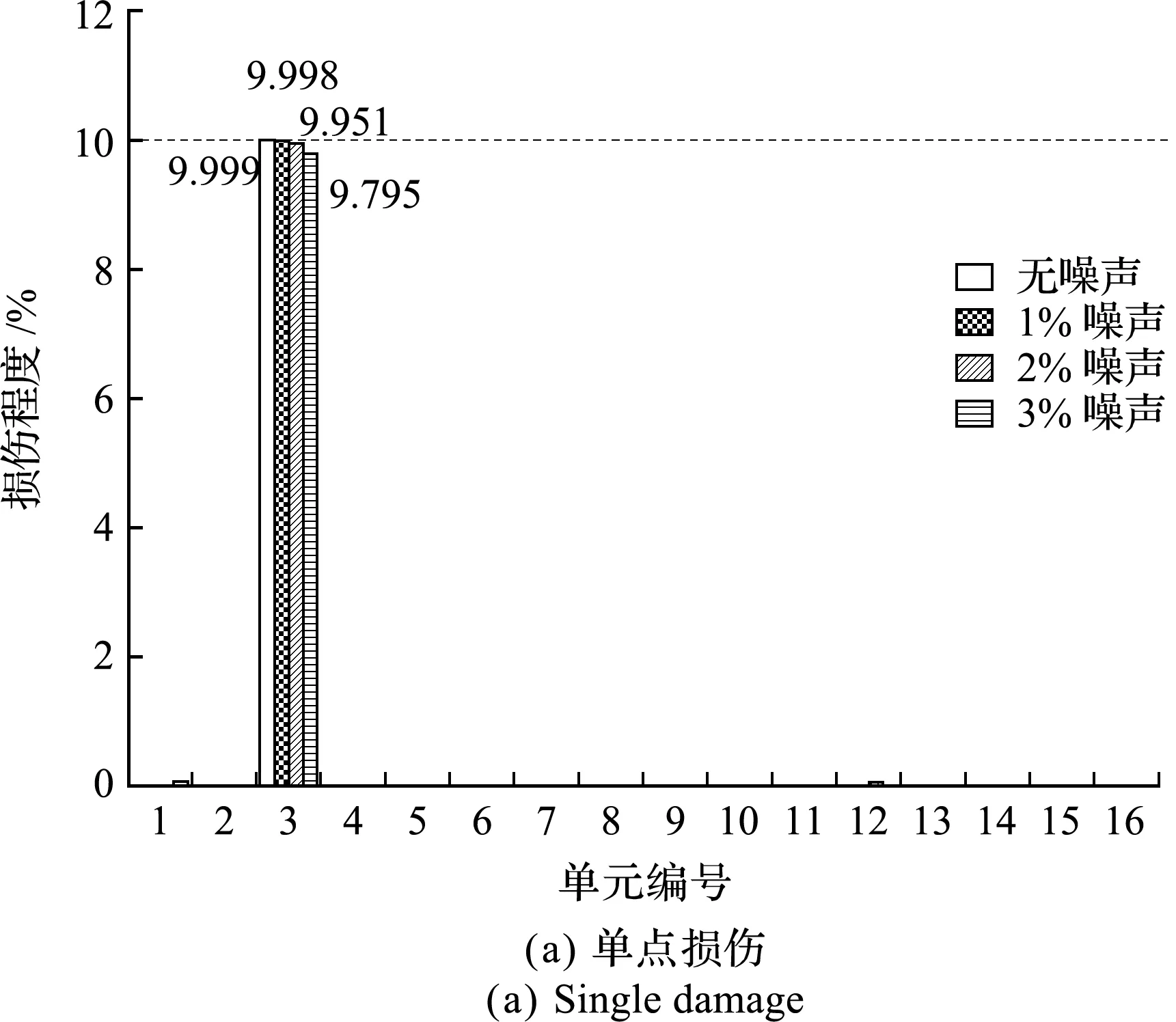
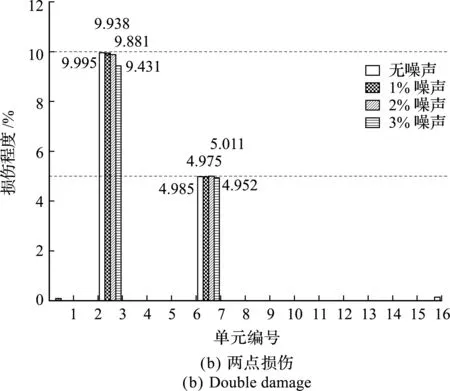
图3 简支梁损伤识别结果

综上所述，利用结构的自振频率信息并结合文中提出的损伤识别方法，可较好地对环境温度变化进行量化，同时也可在温度变化与噪声影响下对结构的损伤实现准确的定位与量化。

5.2 I-40钢混组合体系桥梁工程实例

为进一步验证本文提出的方法，引入I-40钢-混凝土组合体系桥梁[14]。该桥梁在无损状态下进行了一次振动测试，在其北侧腹板及底板处引入了四种不同程度的损伤工况，引入D -1～D -4损伤工况后振动测试时对应的环境温度分别为15.5 ℃,28.9 ℃,26.1 ℃及20.0 ℃，对应的刚度折减比例为5%,10%,32%及92%。基于Matlab平台建立了该桥梁有限元模型(图4)。取该模型前6阶自振频率(Hz)分别为[2.4821,3.0016,3.4176,4.0365,4.0369,4.6561]，相较于实测频率(Hz)[2.4828,2.9593,3.4991,4.0791,4.1668,4.6310]，在不考虑环境温度的情况下，最大误差仅为3.22%，处于可接受范围内。而模态置信度分别为[0.9949,0.9841,0.9905,0.9708,0.9718,0.9709],均在0.97以上，故该模型可作为基准模型验证所提出的识别方法。

图4 I -40桥梁有限元模型及损伤工况

取I-40桥在D -1～D -4损伤工况下实测前6阶频率，按提出的方法进行温度与损伤识别，对于SVR参数设定为C=2000，g=0.18,ε=0.15，训练样本数为1000。EMFO种群大小为150，最大迭代2000次，正则化求解精度ξ=10-5。目标函数与前文一致，但为减小计算量，仅计算两侧腹板单元的模态应变能。针对每种工况运行7次，取识别结果平均值列入表2和表3。

由表2和表3结果可知，提出的方法可较为准确地识别环境温度变化，尤其是D -2与D -3两种工况，其误差分别为1.274 ℃与0.086 ℃。而对于损伤识别，由于引入稀疏正则化，其损伤定位十分准确，程度量化方面较为精准，仅在对称腹板处出现少量误差，其主要原因可归结为,(1) 温度在实际结构中呈现较为明显的不均匀分布； (2) 有限元模型与实际结构存在一定的误差。总体而言，通过本文提出的方法可识别结构温度变化及其内部损伤。

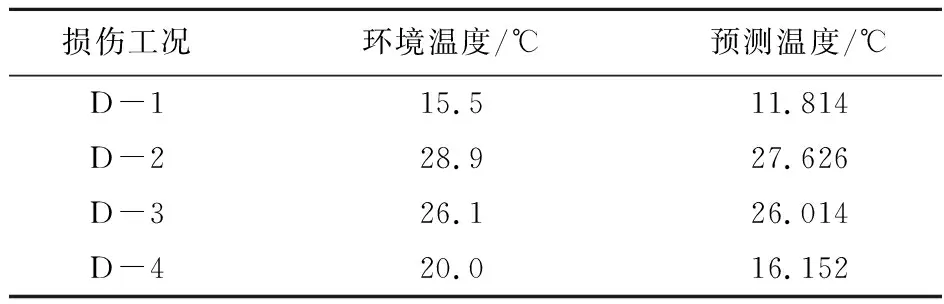
表2 温度识别结果

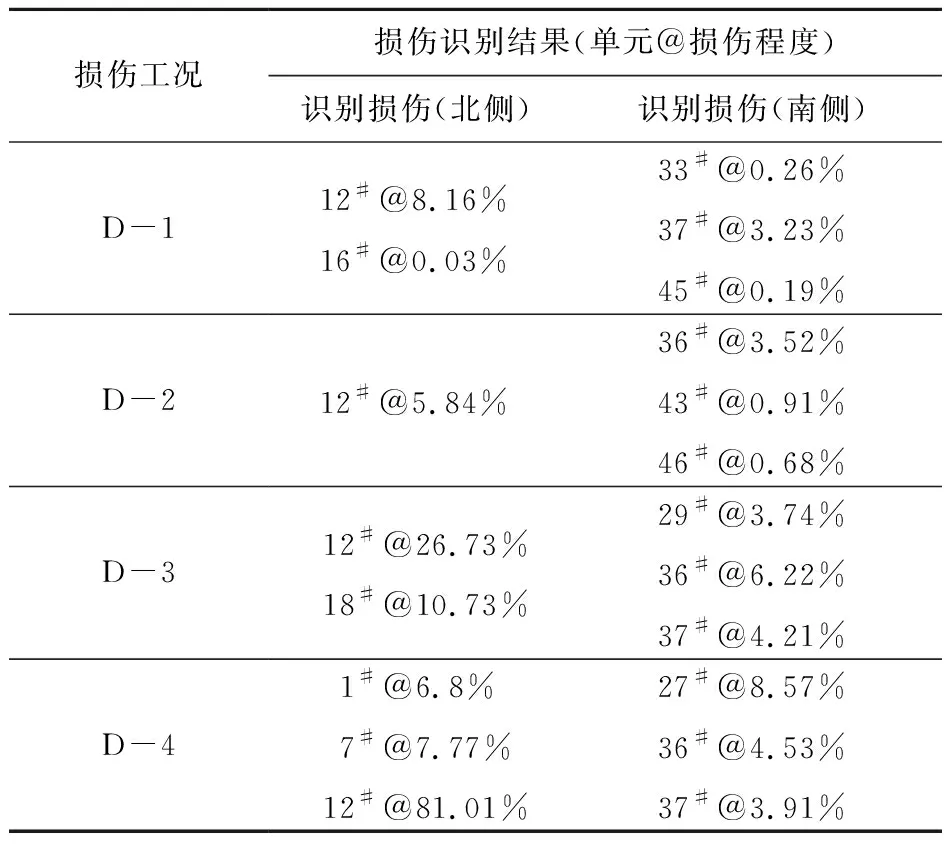
表3 损伤识别结果

6 结 论

(1) 环境温度变化对损伤识别的影响可通过温度-弹性模量变化关系体现，从而提出考虑环境温度影响的损伤识别模型进行量化分析。

(2) 稀疏正则化理论结合灵敏度分析，可解决实际结构中的稀疏损伤识别问题，同时，误差分布阈值法可消除微小计算误差，提高求解精度。

(3) 提出的EMFO算法较MFO,PSO及CS而言具有更快的收敛速度及更强的全局寻优能力。基于EMFO并结合SVR、稀疏损伤识别及考虑环境温度变化的结构损伤识别模型，提出环境温度影响下的损伤识别方法，并通过一考虑环境温度变化的简支梁算例及I-40钢-混组合体系桥梁，验证了方法的有效性。结果表明，提出的方法可对环境温度变化进行准确量化，对不同损伤工况也可实现较为准确的识别，同时在噪声影响下也体现一定噪声鲁棒性。

综上所述，本文提出的方法可量化分析损伤识别中环境温度的变化，并能实现损伤准确识别，具有一定的实际应用潜力。