考虑热力耦合作用的钻削钛合金材料有限元仿真研究

李康帅，朱红梅

1西南石油大学土木工程与测绘学院；2西南石油大学机电工程学院

1 引言

钛合金由于具有强度高、热强度高、耐蚀性好等优点，在飞机发动机结构件、紧固件、骨架及起落架等方面的使用比重逐渐增加[1]。在飞机的制造和装配过程中，目前主要采用螺栓连接方式固定钛合金，因此需要在钛合金板上钻许多孔。采用不同钻孔方式得到孔的精度不同，这对飞机结构连接的准确性和有效性有很大影响[2]。钛合金属于典型的难加工材料，由于其导热性能差、化学活性高，在钛合金孔加工过程中容易出现切屑不易排出、加工表面粗糙、钻具扭断的现象[3]。

目前，针对钛合金材料制孔的加工方法主要有传统一体式钻孔、超声振动辅助钻削、铣削及超声振动铣削。近年来，许多学者对钛合金材料的制孔性能进行了系统研究。在传统钻孔方面，王凯旋等[4]提出一种能够预测微钻削过程切削力的模型，并通过在钛合金板上钻削直径0.1mm的微孔进行仿真和试验研究，验证了该模型的准确性。曹宇等[5]综合现有文献的研究成果，研究了刀具材质、刀具锋角和加工工艺参数对钻孔质量的影响。廖科伟等[6]利用DEFORM-3D软件分析钻削TC4钛合金时，不同转速和进给量对钻削力的影响规律，并用试验验证了仿真结果的准确性。项国辉等[7]通过对损伤容限型TC4-DT钛合金钻削后孔周边残余应力和孔表面粗糙度进行试验分析和有限元分析，研究钻削工艺对TC4-DT钛合金表面完整性的影响规律。安熠蔚等[8]基于DEROFRM-3D软件与单因素试验的对比研究，分析小直径麻花钻在不同主轴转速和进给速度下对TC4钛合金钻削性能的影响。目前，在超声振动辅助钻削方面的研究主要集中于超声振动钻削的钻削力和切屑形态[9，10]、加工质量[11]、加工机理[12]以及加工特性分析[13]。

目前，在铣削及超声振动铣削方面，田卫军等[14]采用有限元仿真方法建立钛合金铣削加工有限元模型，研究不同铣削参数下铣削力和铣削温度的影响。王明海等[15]建立钛合金的超声振动铣削三维热力耦合模型，通过铣削力实验测试验证了模型的准确性。吉春辉等[16]对螺旋铣孔和传统钻孔工艺的加工质量进行了对比。张卫华等[17]利用ABAQUS软件建立TC4材料的三维铣削模型，对铣削温度场和铣削力波形进行了分析。

目前在钛合金钻削制孔工艺的有限元仿真研究中，大部分文献均未考虑钻削过程中热力耦合的作用，而切削力和切削热都是不可忽略的因素。本文基于ABAQUS有限元软件建立钛合金板的钻孔模型，在考虑热力耦合情况和不考虑热力耦合情况下，对比分析不同切削参数的切削力变化，针对合适的切削参数选择给出一定建议。

2 有限元仿真模型

钛合金钻孔过程是一个动态加工过程，在使用ABAQUS软件进行钻孔仿真时，采用专门求解非线性动力学问题的ABAQUS/Explicit求解器进行求解，不考虑热力耦合的钻孔过程使用Dynamic Explicit分析步，考虑热力耦合的钻孔过程采用Dynamic Temp-Disp Explicit分析步。进行仿真分析时，分析部件主要包括钻头和钛合金板。

2.1 建立钻头模型

钻头模型使用直径为3mm的标准麻花钻，在SolidWorks软件建模后导入ABAQUS软件，钻头三维模型见图1。麻花钻材料为YG8硬质合金材料，具有强度高、抗冲击及抗振动性能好等优点，其相关材料参数见表1[18]。在有限元分析过程中，为了简化模型，钻头被视为刚体。

图1 麻花钻三维模型

密度(kg/m3)弹性模量(GPa)泊松比导热率(W/(m·℃))比热容(J/(kg·℃))145006400.2275.4220

2.2 建立钛合金板模型

采用Ti6Al4V钛合金材料进行模拟，其基本性能参数见表2[18]。钛合金圆板直径8mm，厚度3mm。目前主要用于合金等韧性金属材料仿真的本构模型有：Bodner-Paton模型，Johnson-Cook(J-C)模型，Follansbee-Kocks模型等[19]。在钻孔过程中，钛合金会发生一定的塑性变形，J-C模型可以准确预测材料的流动应力，因此选取J-C模型表示钛合金本构关系，表达式为

(1)

此外，在钻孔过程中产生切屑，钛合金材料发生较大的塑性变形，存在一定的金属损伤。为了实现切屑分离，在定义韧性金属损伤时同样采用Johnson-Cook损伤模型[19]。采用基于单元积分节点的等效塑性应变准则，其表达式为

在教学的过程中，教师应该时刻注重知识内容与生活的结合，促进生活化教学模式的构建，实现教学活动的不断优化。生活指导式教学和生活实践式教学，是生活化教学的主要方式。生活指导式教学，就是教师在开展道德与法治教学的过程中，将生活中的小常识或者生活道理融入到教学内容中，帮助学生培养起基本的道德与法治意识。生活实践式教学，则是教师在教学的过程中能够不断引导学生通过直接参与生活的方式，掌握必要的生活技能。

(2)

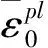
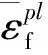
(3)

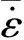
(4)

Ti6Al4V材料本构模型参数和损伤参数见表3。

表2 钛合金的性能参数[18]

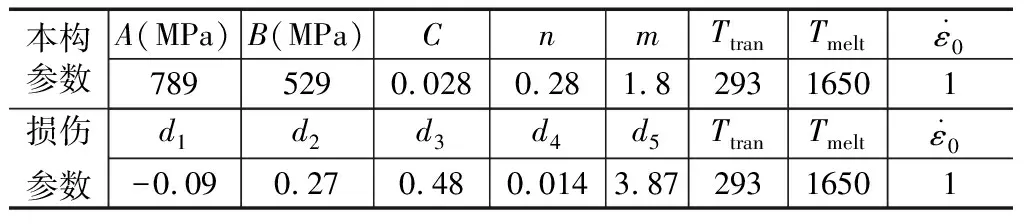
表3 钛合金Johnson-Cook模型参数[18，19]

2.3 边界条件和网格设置

在接触设置时，模型的法向属性设置为硬接触，切向属性设置为罚函数的摩擦模型，钛合金和钻头之间的摩擦系数为0.3。钻削钛合金时，对将钛合金圆板的四边进行全固定(Ux=Uy=Uz=URx=URy=URz=0)，限制钻头X和Y方向的移动和转动，对钻头Z方向施加速度载荷，模拟钻头的进给速度和主轴旋转速度。对于考虑热力耦合情况下的钛合金钻孔过程，需在边界条件中定义钛合金温度场，初始温度设为25℃。

对于不考虑热力耦合情况下的钛合金板钻孔过程模拟，将待加工孔周围的网格加密。对于考虑热力耦合情况下的钛合金圆板钻孔过程模拟，使用ALE自适应网格技术在计算时对待加工孔周围网格进行重新扫掠检测，以保证计算过程中减少单元发生扭曲变形，有助于提高计算结果的准确性。ALE自适应网格(Arbitrary Lagrangian Eulerian adaptive meshing)全称为“任意的拉格朗日-欧拉自适应网格”，是介于完全欧拉分析和完全拉格朗日分析之间的某种方式，材料相对于网格变形，同时网格也变形，但网格可独立于材料变形。

ALE的优点在于不改变原有网格的拓扑结构，即节点和单元的数目以及连接关系不会发生变化，而是在分析步的求解过程中逐步改善网格的质量。此外，对于不考虑热力耦合的钛合金钻孔过程，试件网格单元类型为8节点实体减缩积分单元C3D8R，钻头单元类型为4节点线性四面体单元C3D4。对于考虑热力耦合情况下的钛合金圆板钻孔过程，试件网格单元为8节点实体减缩积分热力耦合单元C3D8RT，而钻头类型为4节点线性四面体热力耦合单元C3D4T。有限元模型见图2。

图2 钛合金钻削模型

2.4 钻孔参数选择

在有限元模型中，改变钻削速度n和每转进给量fr，分析不同钻孔参数对钛合金制孔性能的影响。基于工程中钛合金的钻孔进给量范围为0.1～0.3mm/r，依据单因素参数分析法[8]，采用的相关钻孔参数见表4。

表4 钻孔参数的选择

3 仿真结果分析

使用Explicit求解器对不考虑热力耦合及考虑热力耦合的钛合金钻孔过程进行求解，得到如图3所示的钛合金圆板钻孔仿真过程云图。

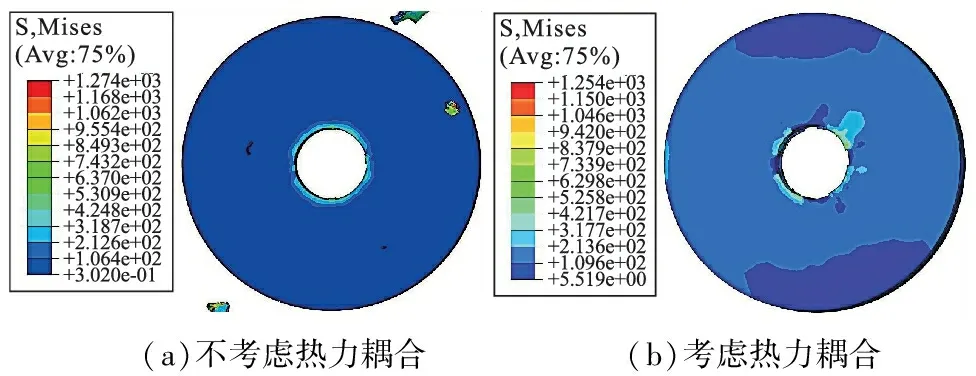
图3 钛合金钻孔过程仿真云图

图4为考虑热力耦合情况下的钛合金钻削过程的节点温度分布云图和单元温度分布云图，两个云图来自同一个钛合金模型(钻削速度为1200r/min，每转进给量为0.1mm/r)。从图中可以看到，在钻孔周围区域的节点温度和单元温度均比远离钻孔区域的温度更高，与实际情况相符。此外，钻孔过程完成后，图4中显示的节点温度和单元温度并非切削过程中产生的最高温度(图4中无红色高温部分)。实际上，这种高温红色部分在切屑中显示，表明钻削过程中大部分切削热被切屑带走，这与文献[14]研究的情况相符，也与实际加工过程相符。

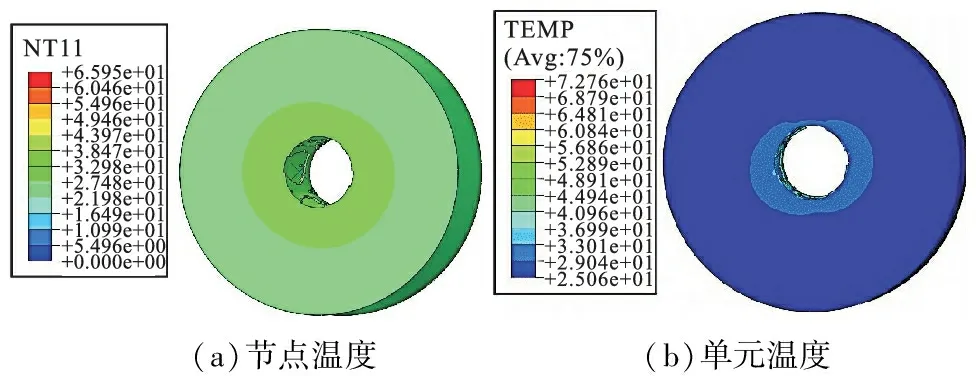
图4 考虑热力耦合时钛合金板的节点温度和单元温度分布云图

钛合金钻孔过程中，考虑热力耦合和不考虑热力耦合输出的轴向力和扭矩见图5和图6。图5为fr=0.1mm/r，n=1400r/min时的轴向力和扭矩变化曲线，图6为fr=0.3mm/r，n=1200r/min时的轴向力和扭矩变化曲线。其余钻孔参数的曲线变化形式与图5和图6大致相同，只是轴向力和扭矩值不同。

(a)轴向力变化

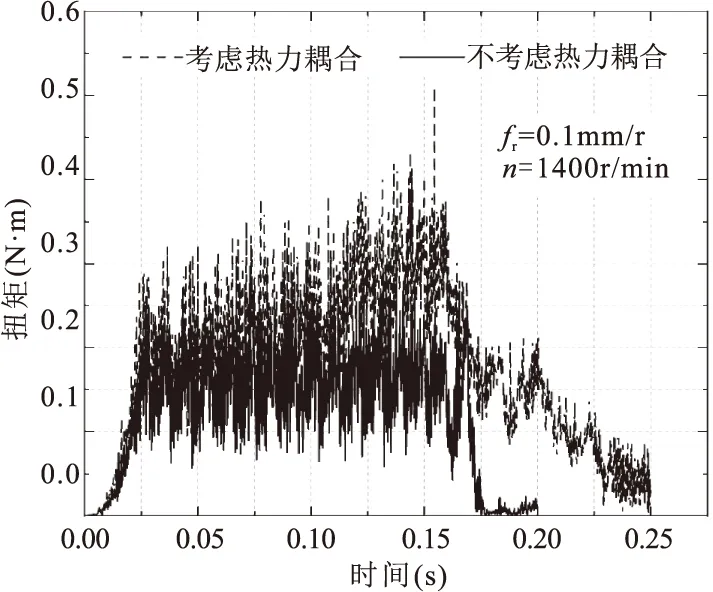
(b)扭矩变化

从图中可以看出，无论是否考虑热力耦合情况，随着钻头逐渐钻入钛合金板中，钻头所受的轴向力和扭矩都逐渐增加，当钻头钻尖钻出钛合金板后，所受的轴向力和扭矩逐渐减小为零。在不考虑热力耦合情况下，当fr=0.1mm/r，n=1400r/min时，轴向力最大值为621N，最大扭矩为0.31N·m；当每转进给量fr=0.3mm/r，n=1200r/min时，轴向力最大值为732N，扭矩最大值为0.58N·m。在考虑热力耦合情况下，当fr=0.1mm/r，n=1400r/min时，轴向力最大值为687N，最大扭矩为0.51N·m；当fr=0.3mm/r，n=1200r/min时，轴向力最大值为861N，扭矩最大值为0.77N·m。

考虑热力耦合影响时的轴向力和扭矩都稍大于不考虑热力耦合影响时的轴向力和扭矩，且轴向力差异较小，而扭矩间的差异大于轴向力间的差异。此外，当钻头钻出钛合金板后，不考虑热力耦合影响的轴向力和扭矩值会逐渐下降至零(或几乎为零)，而考虑热力耦合影响的轴向力和扭矩值逐渐下降后则会稳定在一个小值，并不会下降成零。这是由于在热力耦合分析中，钻头钻出钛合金板之后，工件内部还存在切削热并伴随切削力，该结果在应力云图上也有体现。

(a)轴向力变化

(b)扭矩变化

图7为不同钻孔参数下，钛合金板钻孔过程平均和最大的轴向力变化规律。其中，图7a为当fr=0.1mm/r时改变钻削速度n对钻孔过程轴向力的影响；图7b为当n=1200r/min时，每转进给量fr对钻孔过程轴向力的影响。可以看到，考虑热力耦合时的轴向力比不考虑热力耦合时的更大，但两种情况下得到的最大轴向力和平均轴向力在不同钻孔参数时的变化趋势相同。

当fr=0.1mm/r时，轴向力随钻削速度n的增大而减小。当n从600r/min提升至800r/min，1000r/min，1200r/min，1400r/min时，对于不考虑热力耦合的情况，其对应的最大轴向力分别减小5.42%，5.42%，10.3%，11.3%，其对应的平均轴向力分别减小6.8%，11%，14%，17.4%；对于考虑热力耦合的情况，其对应的最大轴向力分别减小3%，5.93%，8.2%，9.5%，对应的平均轴向力分别减小5.8%，10.8%，13.9%，15.2%。

(a)fr=0.1mm/r时钻削速度对轴向力的影响

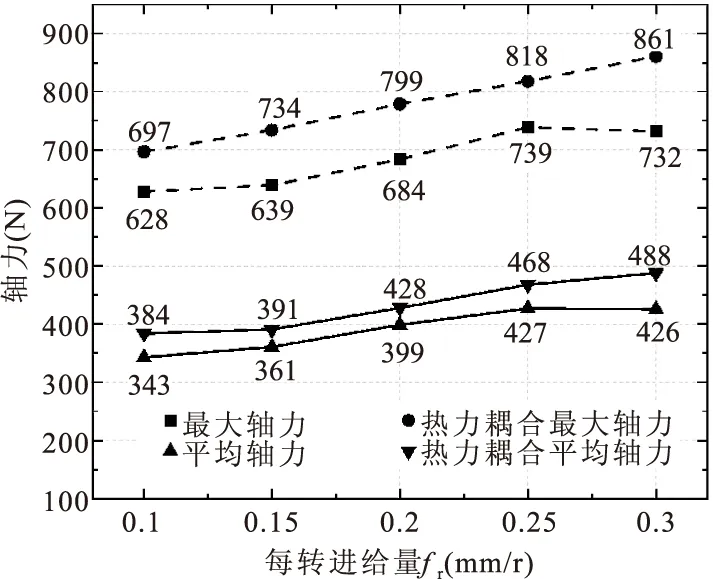
(b)n=1200r/min时每转进给量对轴向力的影响

当n=1200r/min时，轴向力随每转进给量fr的增大而增加。当fr越来越大时，轴向力的变化趋缓。当fr从0.1mm/r提至0.15mm/r，0.2mm/r，0.25mm/r，0.3mm/r时，对于不考虑热力耦合的情况，所对应的最大轴向力分别增大1.8%，8.9%，17.7%，17.7%，对应的平均轴向力分别增大5.2%，16.3%，24.5%，24.5%；对于考虑热力耦合的情况，对应的最大轴向力分别增大5.3%，14.6%，17.4%，23.5%，对应的平均轴向力分别增大1.8%，11.5%，21.9%，27.1%。同样，从这些百分比可以看出，钛合金钻孔过程中每转进给量fr的变化对轴向力的变化影响更大。无论是考虑热力耦合或不考虑热力耦合的情况下，当每转进给量fr为0.1mm/r，钻削速度n为1400r/min时得到的轴向力具有最小值。说明每转进给量越小，轴向力越小；钻削速度越大，轴向力越小。

4 钻削预测模型

利用MATLAB软件结合多元线性回归函数regress，根据钛合金的仿真结果，建立钻削平均轴向力的数学模型。根据切削加工原理，切削力和切削参数之间存在复杂的指数函数关系[8]，钻孔时钛合金的钻削轴向力和钻孔参数间的公式为

(5)

式中，FTi为轴向力；CTi为常数；vf为进给速度，vf=nfr；n为钻削速度；α和β分别为进给速度系数和钻削速度系数。

将式(5)两边取对数有

lnFTi=lnCTi+αlnvf+βlnn

(6)

设y=lnFTi，b=lnCTi，x1=lnvf，x2=lnn，变换后得到

y=b+αx1+βx2

(7)

代入数据进行多元线性回归分析，可以得到相应的回归系数。不考虑热力耦合时的钛合金轴向力回归公式为

(8)

考虑热力耦合时钛合金钻削轴向力回归公式为

(9)

式(8)和式(9)对应的线性回归相关系数分别为0.9734和0.9229。可以看到，两式的线性相关系数都接近1，说明轴向力预测数学模型可用。

图8为理论预测模型与仿真模型的轴向力值，图中不考虑热力耦合情况为仿真值1和预测值1，考虑热力耦合情况为仿真值2和预测值2。

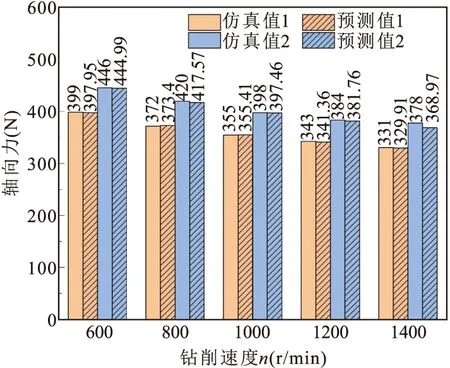
(a)fr=0.1mm/r，钻削速度不同

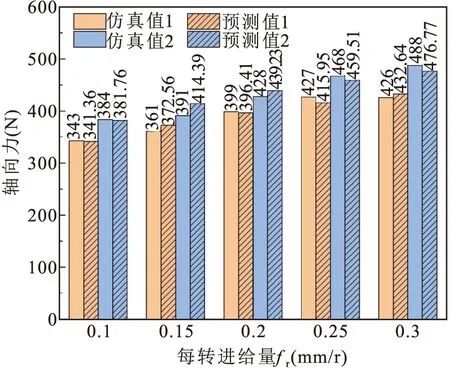
(b)n=1200r/min，每转进给量不同

由图可知，无论是否考虑热力耦合，总体上来说，理论预测模型与仿真模型的差距较小。不考虑热力耦合的模型的仿真值与预测值之间的误差比考虑热力耦合时要小，这一情况在线性回归相关系数上也有所体现。在考虑热力耦合情况时，最大误差为6%，属于可接受的范围。

5 结语

利用ABAQUS有限元软件及ALE自适应网格划分技术建立不考虑热力耦合和考虑热力耦合情况下的钛合金三维钻削模型，分析不同钻削速度和每转进给量时的钻削性能，可以得到如下结论。

(1)在热力耦合模型钻削过程中和钻削完成后存在切削力和切削热，而考虑热力耦合的钛合金钻削模型所得的轴向力和扭矩大于不考虑热力耦合模型得到的轴向力和扭矩数值，在不同钻孔参数时的平均轴向力和最大轴向力曲线的变化趋势基本一致。

(2)相较于钻削速度对钻削钛合金板的轴向力和扭矩影响，每转进给量对钻削钛合金板的轴向力和扭矩影响更大。当每转进给量一定时，轴向力随着钻削速度增大而减小；当钻削速度一定时，轴向力随着每转进给量增加而增加。在实际钻削过程中，采用大的钻削速度和小的每转进给量能够减小钻削钛合金时产生的轴向力。

(3)根据多元线性回归分析得到不考虑热力耦合轴向力和考虑热力耦合钛合金钻削轴向力的经验公式，在两种情况下对比预测值与仿真值，其误差均小于6%。