基于ZigBee技术的地铁隧道纵向不均匀沉降检测方法

曲锐

(中铁九局集团第六工程有限公司, 工管部，辽宁, 沈阳 110000)

0 引言

近些年来，不少城市都修筑了地铁，地铁建成之后，会因为不同埋深、渗漏、不同地质、不同施工因素、列车振动荷载、不同地面荷载等因素导致地铁隧道产生纵向沉降变形[1-2]。地铁隧道的抗纵向沉降能力较为弱小，容易引起隧道不定期地出现不均匀沉降。为了确保地铁的安全运行与延长地铁隧道的使用寿命，对地铁隧道纵向不均匀沉降进行研究与检测就显得尤为关键。不少学者对此进行了研究，取得了一定的进展。卜康正等[3]提出明挖卸荷引起桩侧摩阻力作用下的地铁隧道竖向变形计算，通过双面弹性地基梁模型进行地铁总竖向附加应力计算，能够有效提升地铁隧道变形监测效率，但是缺少预测功能，无法有效预测安全隐患问题。张云毅等[4]提出岩溶破碎带盾构下穿建筑物沉降分析及控制方法，通过施工过程中沉降监测数据对现场沉降控制措施进行评估,该注浆技术可有效控制沉降，但是这种算法较为复杂，难以为工程界所应用。

ZigBee技术在进行通信检测时，通信稳定性不佳，衍射能力较弱，但是将ZigBee技术应用在地铁隧道沉降检测中时能够降低检测成本，并在近距离检测时功耗较低，检测的网络容量较大，同时在进行数据传输时安全性与可靠性都较好，能够提升地铁隧道纵向不均匀沉降检测数据的精准性。为此，本文引入ZigBee技术进行地铁隧道纵向不均匀沉降的检测。

1 基于ZigBee技术的无线检测网络架构

1.1 网络架构

无线网络是一种存在多信道与多逻辑能力的层次型分簇拓扑架构。底层网络结构通过检测区域中的叶子节点[5]与其网络中的父基站节点构成，叶子节点主要检测数据的收集，其即整体无线网络检测架构的基础，父基站节点主要采集子节点的信息，同时将其传输至统一信道的上层簇头内，其即网络信道的底座，上级网络即通过父节点形成的簇头节点与其子收集节点形成的检测网络，簇头节点主要采集检测信息，同时依靠信道向上传输，对整体多信道网络架构层次有着重要的作用，最后检测数据通过Sink节点传输到网关节点，经过串口的形式，把信道里的数据以此传输到终端检测控制器内。

1.2 同步采集

拟定目前的时间戳为T01，同时储存在不同报文1内并进行广播。测节点在得到同步报文1之后，凭借时间计数器，对节点时刻T11进行标记。在延迟10 s之后，在下次报文1开始时，信道管理基站与节点会分别统计同步报文T12与时间戳T02的抵达时间，进而就能够计算出基站与检测节点的相对频率偏差是ais=(T02-T01)/(T12-T11)。节点在T13时刻，把本地时刻校准成T02+ais(nt+(T13-T12))。

2 ZigBee网络下地铁隧道纵向沉降因素分析

2.1 断裂带影响下地铁隧道纵向沉降计算

某地铁隧道在构建时穿越了一条断裂带[6]，由于断裂带长时间的多期活动，其左右两边的岩层产生了相对位移，所以导致了断裂带两侧的下卧土层[7]出现沉降的现象发生。

通过分层总和法运算不同地质条件下地铁隧道的纵向不均匀沉降影响因素，需要进行以下拟定。

拟定1：列车在轨道中长期运行，运算时把地铁承载的地铁振动荷载等效进行均匀分布处理。

拟定2：地铁隧道下的土体测量不会产生横向变形，只会出现纵向变形。

通过分层总和法运算隧道不均匀沉降计算的过程如下所示。

(1)土的分层。拟定成层面与地下水面当作分层面。

(2)运算所有分层土的自重应力。土的自重应力从天然地面开始起算。

(3)确准地基沉降深度。附着的应力会随着不断提升的深度而出现递减，在达到一定值之后，附着的应力会变成零，引发的压缩变形能够不做考虑[8]。

(4)运算断裂带影响下各层土的压缩模量ΔSi。用用时εi代表第i层土的压缩应变，Hi代表第i层土的厚度，e1i代表i层土的上层与下层自重应力的平均值，e2i代表i层上层与下层附加的土自重应力平均值与应力平均值总和，Δei表示i层土与下层自重应力的空隙比变化量，ai代表第i层相应的压缩系数，Esi代表第i层相应的压缩模量。具体计算式为

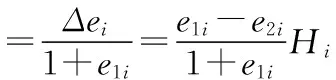
(1)

式中，p1i表示i层土上层与下层附加应力，p2i表示i层土纵向附加应力，ΔPi代表i层土的附加应力变化量。

(5)预算总沉降量s。总沉降量等于各层沉降量的总和。

2.2 地下水位影响下地铁隧道纵向沉降计算

2.2.1 地下水位变化下土体压缩模量

在降雨的流程内，因为面积较大，近似认定需要在完全侧限的情况下进行，拟定竖向应力增加Δp，那么对应的应变就需要增加Δε，凭借这个定义能够获得：

(2)

其中，Es代表土体侧限压缩模量[9]，ΔH代表沉降前和沉降之后的高差。

使用三项比例指标计算图对所有指标之间存在的关联进行计算，拟定土体颗粒体积是Vs=1，土内空间缝体积是Vv=e，降水前土内空隙体积是Vv=e1，降水之后土内空隙体积是Vv=e2。

那么在无侧向变形的状态下，就是横截面积不出现变化的状态下，根据土粒所占高度不变的条件，ΔH就能够通过对应的空隙比的变化Δe=e1-e2来进行描述。

(3)

以此获得：

(4)

把式(4)代入式(2)内得到：

(5)

式中，

(6)

其中，a代表压缩系数，与压缩模量Es相同，其都不是常数，会随着压力的大小产生改变。

2.2.2 基于附加应力算法的地层沉降值计算

对土骨架支架存在的应力进行分析，拟定在干燥土层内，其自重应力的方向为垂直方向，并呈现直线分布，其应力的计算方程能够描述为

σ=γH

(7)

其中，γ代表土体饱和容重，H代表水平面至土体表面的尺寸。

假如地下水水位和地下水线处于平等状态，土体处于地下水位线之下，那么其应力就与其自重减去其所承受的水浮力相同，因此应力σ的计算式为

σ=(γsat-γw)H

(8)

其中，γsat代表土体饱和时的容量，γw代表水的容重，其取值是9.8 N/m3。

假如地下水位线高于地下水位，地下水位线上方没有毛细水，那么其应力分布就能够通过OK曲线段进行描述，在水位线下方的应力分布就能够通过KF曲线进行描述，这2条曲线是相互平行的，假如地下水位出现下滑，水位线下降到最底层的地下水位线，那么土体应力的分布就需要通过OB曲线进行描述。在土层内，因为地下水的流失，使得地层的附加压力出现上升，导致地层的沉降值产生上升，继而干扰地层的沉降范围和沉降量。地层的沉降量能够凭借式(9)进行计算：

(9)

把式(6)引入式(9)能够得到：

(10)

其中，ΔP代表地层的附加应力，H代表压缩层厚度，a代表压缩系数，e1代表土的原始孔隙率。

由此能够看出，在地下水位产生变化时，地层的附加应力也会随之产生变化，继而干扰地层的沉降量。

3 地铁隧道纵向不均匀沉降检测实现

地铁隧道对纵向曲率的半径与环缝的张开量存在一定限制，纵向曲率半径为ρ≥15 000 m；依靠地铁隧道构建的防水原则，将环缝张开值拟定为δ≤2 mm；接缝内密封点不能漏水，要求δ≤6 mm。依靠材料强度要求，螺栓有屈服强度与极限应力，混凝土需要存在抗拉强度与抗压强度等。

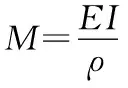
在纵向不均匀沉降的过程内，达到临界值的顺序也是互不相同的。在地铁隧道的曲率半径上升到界限值15 000 m时，环缝张开量只是0.3 mm；而在相同的曲率半径条件下，不同地质的地铁隧道环缝张开量可能是1.0 mm或1.9 mm。这就需要结合上述压缩模量对地质影响因素数值的计算结果来得到其具体的环缝张开量，以环缝张开量作为标准值，如果地铁隧道沉降达到了该环缝张开量，那么就证明，该地铁隧道的沉降属于不均与沉降。

4 实验证明

为了证明所提算法的实用性，进行实验，拟定某一地铁隧道，在该隧道的四周并没有安放沉降观测点，现场对隧道地基梁进行闭合水准观测，E列通过邻近建筑遮挡只能够观测到5～40轴，实测地基梁相对高差的曲线如图1、图2所示。

图1 A列相对高差

图2 E列相对高差

通过图1、图2能够看出，所有检测点都存在不同程度的沉降：A列的沉降相对集中在中间区域，其最大差值为30 cm；E列的沉降也集中在中间区域，最大差值为10 cm。对整体架构来说，A列沉降比E列沉降要相对严重，其沉降的原因主要与地下水位线存在关联。

为了进一步证明所提方法的有效性，以A列40轴线处轨顶表高当作基准，对隧道顶端标高进行现场实测，实测隧道梁相对高差数据如图3～图5所示。

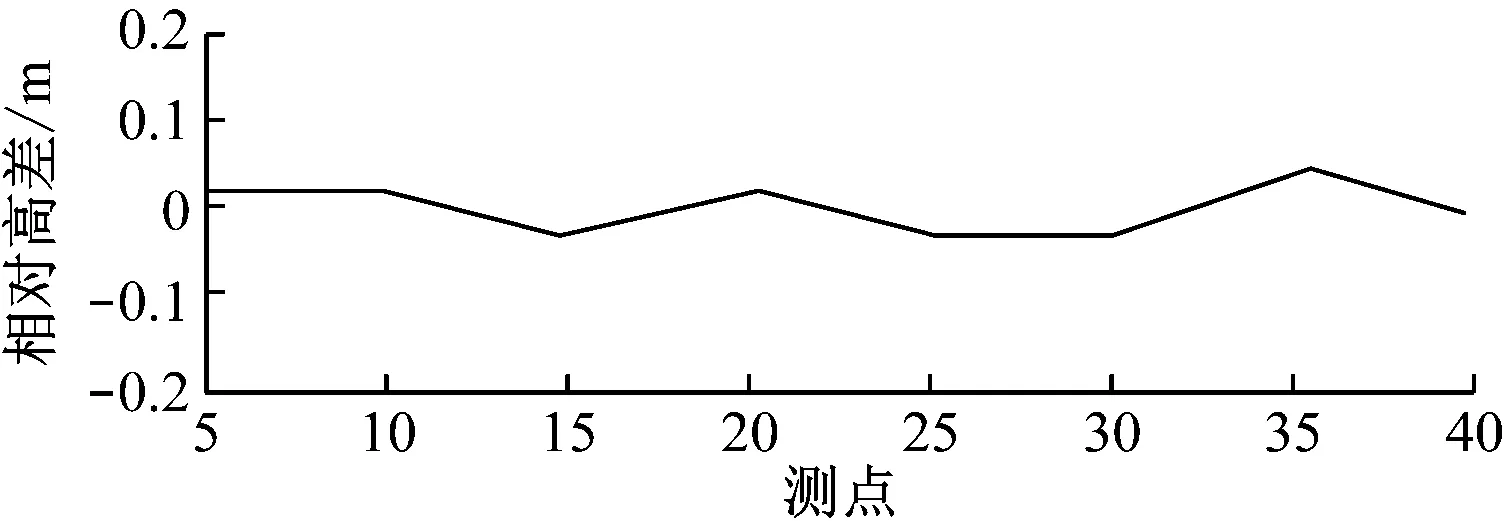
图4 E列各轴相对高差

图5 AE同轴线各轴相对高差

通过图3～图5能够看出，地铁隧道出现扭曲，并出现了较大沉降，地铁隧道出现20 cm横向不均匀沉降差与23 cm纵向隧道最大沉降差，A列相较于E列的沉降更大，这会严重干扰顶梁的正常使用，说明地铁隧道出现了严重的不均匀沉降。

5 总结

文章提出基于ZigBee技术的地铁隧道纵向不均匀沉降的检测方法，通过实验可知，此方法能够定量分析沉降指数，检测精度高。但因为所提方法的构建是依附于ZigBee技术的无线传感器网络基础的，这就导致如果无线传感器节点出现传输波动，就会导致检测的结果产生微小的误差，虽然这些误差并不会造成较大的影响，但是为了检测结果的可靠性，还需要对其进行优化。